二维水平通道内流动沸腾换热的格子Boltzmann模拟

2023-10-26孟凡星程显耀李维仲

计算力学学报 2023年5期

孟凡星, 董波*, 程显耀,2, 秦妍, 安祥, 李维仲

(1.大连理工大学海洋能源利用与节能教育部重点实验室,能源与动力学院,大连 116024;2.中车大连机车研究所有限公司,大连 116021)

1 引言

流动沸腾广泛存在于能源动力、石油化工、低温制冷、航空航天及冷却电子设备等领域[1]。壁面过热度、通道尺寸和入口流速等因素对流型和流动沸腾换热特性有重要影响,并直接影响设备运行安全。因此,研究各因素对沸腾换热过程的影响规律具有重要意义。

国内外诸多学者已经对流动沸腾换热特性展开了大量研究。实验方面,Jakubowska等[2]发现制冷剂HFE7000在光滑垂直通道内传热系数随热流密度和饱和温度增加而增加,而质量流量对传热系数没有显著影响。Jige等[3]指出对于制冷剂R32在水平小口径管内流动沸腾而言,传热系数随管径减小而增大。数值模拟方面,Mukherjee等[4]基于Level-set方法指出流动沸腾过程中平均换热系数随壁面过热度增大而增大。Zhuan等[5]采用VOF方法分析了气泡生长及分离与聚合对微通道内水的流动沸腾换热过程的影响。

Level-Set和VOF方法需在初始时刻假设小气泡存在,因此无法实现对气泡成核过程的模拟。近年来,作为介观模拟方法的格子Boltzmann方法LBM(Lattice Boltzmann Method)因具有物理意义清晰、边界条件处理简单和程序易于实施等特点而受到研究者广泛关注。现有多相LB模型主要包括颜色模型[6]、伪势模型[7]、自由能模型[8]和相场模型[9],其中,伪势模型通过引入一种伪势直接描述不同相态间粒子相互作用,进而反映多相流体动力学物理本质,是目前应用最为广泛的一类模型。与Level-Set和VOF方法相比,伪势模型可模拟成核过程,并可实现气液相界面自动生成和演化,因此,其在模拟多相流和相变换热时具有很大优势。Gong等[10]提出一种针对能量方程中相变源项的解决方案,提高了数值稳定性。在此基础上,模拟了微通道中饱和流动沸腾中气泡形成过程[11]。Sun等[12]基于上述模型对水在竖直管内流动沸腾过程进行了研究。Li等[13]通过构造外力格式,对伪势模型的力学稳定性条件进行调整,实现了伪势模型的热力学一致性。而后,Li等[14]对原模型进行改进,消除了恢复到宏观方程存在的误差项及源项的离散效应。

流动沸腾不仅涉及两相流体在流道内流动,而且在相变过程中还伴随能量传递。流动和换热二者之间相互关联和影响,使得流动沸腾的模拟更加困难。此外,与众多池沸腾的数值研究相比,目前关于流动沸腾换热的模拟仍然有限。因此,本文采用LBM对二维水平通道内水的流动沸腾换热过程进行数值研究,并通过改变壁面过热度、入口流速和通道宽度等因素分析流动沸腾过程的换热特性。

2 数值模型

采用多松弛MRT(Multi-Relaxation-Time)双分布函数模型对二维水平通道内流动沸腾现象进行研究。该模型通过求解密度分布函数和温度分布函数,可实现对速度场和温度场的模拟。

2.1 MRT伪势LB模型

密度分布函数的演化方程为

fα(x+eαδt,t+δt)=fα(x,t)-(M-1ΛM)αβ(fβ-

(1)

(2)

(3)

(4)

(5)

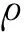
(6)

(7)

总作用力项F=(Fx,Fy)由粒子间相互作用力Fint和流固作用力Fads构成,即

F=Fint+Fads

(8)

对于单组分多相流,粒子间相互作用力Fint为

(9)

(10)

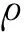
(11)

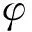
2.2 MRT热LB模型

温度分布函数的演化方程为

gα(x+eαδt,t+δt)=gα(x,t)-(M-1Λ′M)αβ×

(12)

Λ′=diag(s0,s1,s2,s3,s4,s5,s6,s7,s8)

(13)

(14)

(λT)-·(kT)

(15)

(16)

迁移步由式(17)给出,

(17)

(18)

2.3 液滴蒸发定律验证

液滴蒸发定律(D2定律)是涉及相变的数值模拟研究中的经典算例,即液滴直径平方随时间呈线性变化。网格数选取200×200,定容比热容cV=5.0,导热系数λ=2/3。如图1(a)所示,初始时刻,在计算域中心放置直径为D0=60的静止液滴,饱和温度为Ts=0.86Tc,气体温度Th=1.25Tc,四周边界均采用周期性边界格式。随着热量由四周向液滴内部传递,液滴直径有所减小。如图1(b)所示,液滴直径与初始直径之比的平方与时间呈线性关系,这与D2定律十分吻合,因此验证了本文程序的正确性。

图1 D2定律验证Fig.1 D2 law validation

3 模拟结果与分析

3.1 初始条件与边界条件设置

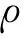
图2 计算域Fig.2 Computational domain

为便于分析各因素对沸腾换热过程的影响,引入下列物理量。壁面平均换热系数h(t)为

h(t)=q(t)/ΔT

(19)

(20,21)

3.2 不同壁面过热度下流型和换热特性

图3 不同壁面过热度下的流型Fig.3 Flow patterns under different wall superheat

图4 不同壁面过热度下的平均热流密度和平均换热系数Fig.4 Average heat flux and average heat transfer coefficient under different wall superheats

3.3 入口流速对沸腾换热特性的影响

本节Umax分别为0.005,0.0125,0.025,0.05,0.075和0.1,ΔT=0.0125,W=100。图5为当Umax=0.0125时气液相界面分布。可以看出,壁面附近气泡持续生长并发生聚合,逐渐达到与通道宽度相当的尺寸。由于忽略重力影响,气泡脱离主要依赖于液相拖曳力,表面张力则倾向于使气泡留在壁面上。曳力难以克服粘性力将气泡带离壁面,导致气泡尺寸不断增大。然而,由于通道宽度的限制,气泡无法沿宽度方向继续生长,只能沿长度方向拉长,此时流型呈现出受限气泡流特点。此外,与弹状气泡和壁面间存在一层薄液膜现象不同,此时气泡直接与壁面接触。如图6所示,当Umax=0.05时,上下壁面处气泡逐渐合并形成弹状流。如图7所示,当Umax=0.075时,较多小气泡生成,并在流道出口附近聚合。由此可知,提高入口流速能够促进气泡从壁面脱离,并使主流区气泡尺寸有所减小。

图5 Umax=0.0125时气液相界面分布Fig.5 Vapor-liquid interface distribution for Umax=0.0125

图6 Umax=0.05时气液相界面分布Fig.6 Vapor-liquid interface distribution for Umax=0.05

图7 Umax=0.075时气液相界面分布Fig.7 Vapor-liquid interface distribution for Umax=0.075

不同入口流速下壁面平均换热系数h随时间变化如图8所示。当Umax>0.05时,h较高,改变入口流速对h影响较小。当Umax=0.025时,h随t略有上升而后下降,且与Umax>0.05时相比h有所减小。对于Umax=0.005和0.0125两种工况,换热过程中h逐渐减小,在前180000步二者h基本趋于一致,180000步后,Umax=0.005时换热系数下降速率加快,h大大降低。如前所述,其原因是当入口流速较低时,气泡在壁面附近持续生长却难以脱离,大量气块附着在壁面导致热量难以穿过该区域,最终核态沸腾受到抑制,换热性能有所下降。

图8 不同入口流速下壁面平均换热系数随时间的变化Fig.8 Variation of the average heat transfer coefficient of the wall with time under different inlet velocities

3.4 通道宽度对沸腾换热特性的影响

本节W为50,75,100,150和200,ΔT=0.015,Umax=0.05。图9～图11为不同通道宽度下气液相界面分布。当W=200时,在流道内观察到大气泡,流型为泡状流,沸腾处于核态沸腾阶段。当W=100时,气泡逐渐合并形成弹状气泡,流型处于由泡状流向弹状流过渡的阶段。当W=50时,流道内主要以弹状气泡为主,其原因是当通道宽度减小时,气泡很容易就生长到和通道尺寸相当大小,由于受到通道宽度限制,气泡沿通道长度方向继续生长。

图9 W=200时气液相界面分布Fig.9 Vapor-liquid interface distribution for W=200

图10 W=100时气液相界面分布Fig.10 Vapor-liquid interface distribution for W=100

图11 W=50时气液相界面分布Fig.11 Vapor-liquid interface distribution for W=50

图12为不同通道宽度W下壁面平均换热系数h随时间的变化。随着W减小,h有所增加,当W减小至75和50时,改变W对h影响较小。这是由于当入口流速一定时,减小W导致工质质量流量有所减小,相同时间内加热更少质量流体并使之汽化需要更少热量,因此,在相同ΔT下,W越小越容易发生汽化。随着气泡生成数量增多,核态沸腾得到强化,h有所提高。