基于物理界面的双重介质有限裂隙渗流模型

吴 璇, 沈文豪*, 王志华, 黄隆州

(1.太原理工大学 应用力学研究所,太原 030024; 2.太原理工大学 机械与运载工程学院,太原 030024)

1 引言

含裂隙多孔材料的渗流可以在很多工程领域中遇到,目前常见的模型有经典连续介质模型[1]、双重孔隙度和双重渗透率模型[2,3]以及离散裂隙模型[4,5]等。连续介质模型根据裂隙面的开度和方位修正了Darcy定律的渗透率,能够描述裂隙面导致的各向异性渗流,在包含多裂隙的问题中只需要逐个将各裂隙面引起的渗透率的增量线性叠加[1],即

(1)

式中ni为第i条裂隙的单位法向矢量,Δni为第i条裂隙的开度,I为二阶单位张量。在描述跨尺度的渗流问题中需要考虑更多的细节,如裂隙的边界、裂隙面的曲率和裂隙面的粗糙度等,需要使用各种办法考虑这些细节以提升计算精度[6-9]。

离散裂隙模型[4,5]解决了多个裂隙面内流体输运问题。该模型将渗流空间分割并抽象为裂隙面网络,忽略固体内部的渗流流量,仅考虑网络内部的流体流动。一些流-固耦合问题中多孔介质和裂隙面耦合在一起,如油气开采、地热利用和碳封存中水力裂隙扩展问题[10-12],需要同时处理多孔介质块体和裂隙面内的流体输运。离散裂隙网络是二维空间,而多孔介质是三维空间,要将二者联系在一起,需要将裂隙面当作三维空间的边界,通过守恒关系建立两个空间上运动学和动力学量的联系。这种方法具有很好的精度[13,14],然而对于一些不能方便处理二维和三维流场耦合的计算方法,如纯Lagrange型无网格粒子类方法[15,16],大规模的裂隙面会使计算变得繁重。

裂隙是一个二维曲面,将其置于三维的多孔连续介质中需要定义一个三维的裂隙体的概念,也就是需要根据裂隙内流体的量构建一个有限厚度的界面。在这个有限厚度的界面上,流体信息需要等效于原始裂隙内的物理量信息。在表界面力学中区分物理界面和数学界面[17],如图1所示,宏观上看界面两侧的物理量间断,在数学上为不连续的零厚度的面,而在微观上看界面具有一定厚度,和两相材料的物性以及受力条件相关。

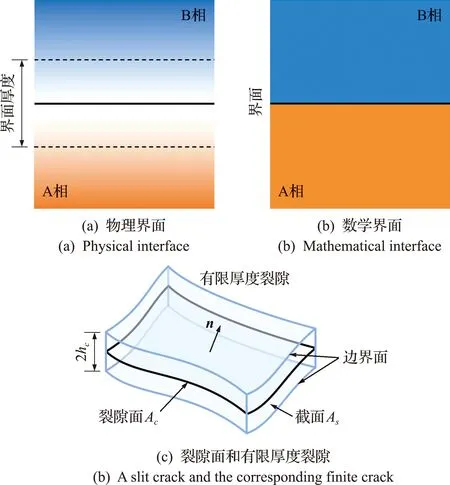
图1 界面和有限厚度裂隙Fig.1 Schematics of interface and finite crack

受物理界面的启发,提出一个有限厚度的裂隙模型,如图1(c)所示,有限裂隙厚度为hc,距离裂隙面越近的流体微团的性质越接近裂隙内的流体微团的性质,在边界面上退化到多孔介质内流体微团的性质。该模型将二维的裂隙面和三维的多孔介质联系在一起,把裂隙面微元看作是多孔介质体微团的一部分。

2 双重介质有限裂隙模型

构造一个不需要修正控制方程的统一模型,将一个二维-三维混合问题简化为纯三维的问题。建立该模型主要分为三步骤。

(1) 将二维裂隙内的物理量通过对应广延量守恒等效的办法转化为三维空间内的物理量。

(2) 等效的流场和多孔介质的流场耦合,形成统一的控制方程和初始-边界条件。

(3) 将计算结果通过步骤(1)的逆过程传回裂隙。

2.1 裂隙流场在三维空间的等效流场

将裂隙面当作多孔介质的一部分可以有效地避免处理二维和三维流场的耦合。如在使用损伤力学处理含裂隙的问题时,将渗透率定义为损伤变量的函数[18,19];使用相场动力学模拟时,流体输运的性质由相参数间接确定[20]。这些方法首先要解决的问题是将基质和裂隙面内的流体流速统一起来,流经某个含裂隙的多孔介质微团的总流量为

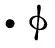
(2)

(3)

下标c为裂隙流体。式(3)和微团尺寸相关,在数值计算中体现为和网格尺寸相关,这由裂隙面和多孔介质的维度不同导致,需要解决广延量守恒性的问题。

(4)

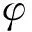
(5)

这种表示方法类似SPH的核近似[15],选用SPH核函数为权函数W(x-xc;h)。权函数需要满足一些附加条件,如归一性、紧致性、非负性、单调递减、对称性、光滑性和在h→0时趋近于Dirac函数的性质。所以权函数满足在裂隙面上取值最大,随着与裂隙面距离的增加取值逐渐减小,并且其积分值为1(图2)。

图2 物理量从裂隙面到对应有限裂隙的定义域延拓Fig.2 Extended domain of definition of quantity from a slit crack to the corresponding finite crack

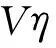
并非所有的物理量都可以使用式(5)延拓其定义域。一些同时出现的多个物理量的组合不能简单地用式(5),如使用压强和速度计算流体做功功率,物理量延拓之后的乘积与物理量乘积的延拓并不相同。解决办法是判断各物理量在裂隙内和多孔介质内的差异,认为差异不大的物理量在有限裂隙和多孔介质内保持相同值,如弱可压缩流体的密度变化不大。这些缓变量Ψ可定义为

(6)

与式(5)对比可知,当待求点远离裂隙面时,或者积分区域截断时,抑或选取有限裂隙面的半厚度hc与网格尺寸相比过小时,物理量Ψ都可以有效地趋近于原始裂隙面上的物理量。

2.2 有限裂隙和多孔介质原有物理量的耦合

建立一个统一的控制方程,将裂隙面内的流体输运方程延拓至三维空间,并与多孔介质本身的物理规律结合起来,物理量定义域的延拓按照不修改三维空间中控制方程形式的原则。在二维和三维空间中流体输运方程具有相似形式,都可以表示为流速和压强梯度之间的关系,在Darcy定律和Darcy-Forchheimer方程等表现为不同渗透率。本文模型以Darcy定律为例。多孔介质内和裂隙内的控制方程分别为

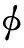
(7)

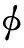
(8)

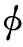
(9)

则多孔介质内和有限裂隙内的流体输运控制方程满足相同的形式,即式(7,9),以此为基础构建统一的流动控制方程。为了保持物理概念描述清晰且不失有效性,假设骨架不随流体流动发生变形或者运动,所以诸如孔隙度和渗透率等物性参数不随时间发生变化。

本模型基于物理界面认为多孔介质内的流体和有限裂隙内的流体完全混合,形成一个新流体的流动。类比两物体的完全非弹性碰撞可知,这种耦合导致各部分流体的流动细节信息丢失,混合后动能有损失,如果讨论热力学和传热学过程,两种流体的混合导致内部存在热量交换,系统熵增加。由混合引入的差异在两流场参数相差较大时可以忽略。

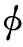
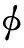
(10)

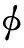
(11)

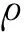
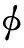
(12)

κf(x)=κfc(x)+κfp(x)

(13)

为了使方程封闭,需要补充连续性方程、描述流体密度改变的本构方程及初始和边界条件。对于弱可压缩流体的流动

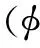
(14)

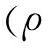
(15)

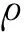
2.3 有限裂隙物理量向裂隙和多孔介质内的转换

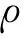
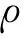
(16)

(17)

积分区域As和ls分别为有限厚度裂隙的截面和该截面沿裂隙面方向的长度,如图1所示。式(17)代表着变换前后裂隙流体流量相等,虽然物理意义明确,但是计算时需要合理选取有限厚度裂隙截面As,不容易直接应用。考虑到任意物理量都是基于式(5,6)将定义域延拓到更高维空间,所以可以取这两式的近似逆函数,得到

vc(xc)=kvf(xc),k=1/[Δc(xc)∬AcW(x-xc;h)dAc]

(18)

式中vf(xc)为计算结果通过插值得到三维空间内点xc处的速度。对于平直的裂隙面,系数k为常数,不同核函数W对应不同的系数k,一般可以直接手动积分获得。式(18)的优势在于计算简便,并且可以不通过数值积分直接得到裂隙内的流速。

将压强计算结果直接代入式(19)获得多孔介质内的物理量信息

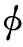
(19)

3 数值方法

选取SPH的指数型核函数作为插值函数,将物性参数定义域从裂隙面上拓展到整个实体空间,

(20)

式中r=|x-xc|为裂隙面上一点xc到待求点x的距离;h为光滑长度,数值越小代表物理量分布集中在中心位置的程度越高;指数型核函数的定义域为[0,∞),所以有限裂隙半厚hc应取完整流场,但是实际计算中可以根据结点间距或者光滑长度选取,如hc=3Δl。改变hc和h可以控制有限裂隙厚度和插值函数的紧致性,如图3所示。

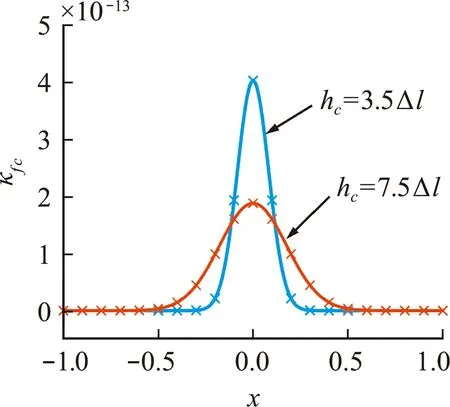
图3 平面裂隙在三维空间的等效渗透率(Δl=0.1,hc=3h)Fig.3 Equivalent permeability in the three-dimension space corresponding to a planar crack (Δl=0.1,hc=3h)

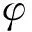
(21)

(22)

控制方程的求解可以使用各类经典方法,本文对三维空间的求解采用有限差分方法,使用等间距的六面体网格离散,并选取19点差分格式;对于二维平面问题和轴对称问题使用四边形网格离散,并选取9点差分格式。动态问题的时间积分使用四阶龙格-库塔公式。

(23)

当z=0时,等式右端的计算值和空间维度无关

(24)

将之和式(18)对比可得

k=1.77245(h/Δc)

(25)

式(25)对二维和三维问题均适用。对于正方形或正方体网格,当hc=3h=3.5Δl时,通过式(25)计算结果的相对误差为 2.4×10-4。

使用有限裂隙模型求解裂隙-多孔介质耦合渗流问题的具体步骤如下。

(1) 使用式(26)计算裂隙面的渗透率

(26)

(2) 使用式(5)延拓裂隙孔隙度和渗透率,使用式(6)延拓初始-边界条件中的密度、速度和压强。

(3) 使用式(10,11,13)耦合有限裂隙和多孔介质内的孔隙度、渗透率、密度、速度和压强。

(4) 使用统一的控制方程(12,14,15)计算整体的流动参数场,对于不可压缩流体,式(14)中密度为常数,并且忽略式(15)。

(5) 使用式(16)计算裂隙内的密度和压强,使用式(17)或式(18)计算流速,使用式(19)计算多孔介质内的流速。

4 数值案例

以典型实例的形式分别对平面问题、三维问题和轴对称问题介绍有限厚度裂隙模型的应用方法,并验证模型的有效性。各验证算例中使用的参数列入表2。当Δl=0.1 m,hc=3h=3.5Δl时,多孔介质孔隙度是有限裂隙等效孔隙度的414倍;有限裂隙内等效裂隙流量是多孔介质自身流量的97.5倍,满足有限裂隙模型的假设。

表2 数值算例中的重要参数Tab.2 Some major variables in the numerical tests

4.1 平面裂隙

首先使用一维流动来验证模型的有效性。在边长为2 m的正方体内存在一水平方向的平面裂隙,弱可压缩流体在压强驱动下在多孔介质和裂隙内流动。压强边界条件满足

p(-L,y,z,t)=1×106Pa,p(L,y,z,t)=0

(27)

流体沿x轴方向流动,该流场可以看作三维或者二维。计算过程需要合理设定时间步长,由控制方程易知等效的非均质材料的特征时间为

(28)

特征时间随不同位置的渗透率变化,为了保证计算稳定,时间步长小于较短的特征时间。本文使用增加裂隙面的方式,将裂隙面向边界外延拓hc的距离,消除了边界引入的截断误差。

分别通过式(17,18)计算流动达到平衡状态时裂隙面上的总流量,二维和三维计算结果的最大相对误差分别不高于0.23%和0.02%,证明在一定精度范围内式(18)满足计算要求。图4绘制了裂隙面内压强分布和解析解的对比,说明有限裂隙模型对于动态问题有很高的精度。

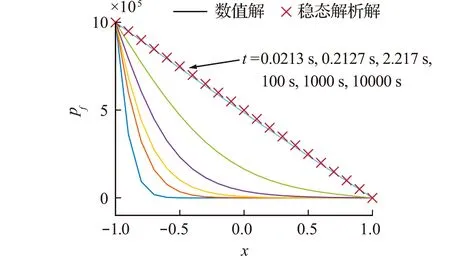
图4 压强沿流动方向的分布Fig.4 Distribution of the pressure in the fluid flow direction

4.2 弯曲裂隙

本算例为Oxy平面内弯曲裂隙内部压力驱动的流动问题,沿x和y方向的流场边界分别为4 m和2 m,裂隙面的参数方程为

(29)

裂隙面上各离散的结点间距为 Δl=πRΔs,各结点的自然坐标为si=(i+1/2)/(N+1),N为裂隙离散的单元个数,R=1 m。边界条件为

p(r,2H)=0,p(r,0)=1×106Pa

∂p(0,y)/∂x=∂p(4R,y)/∂x=0

(30)

渗透率通过方程(26)计算。

弯曲的裂隙面增加了求解难度,主要体现在材料物性参数随空间的不规律变化,以及计算结果向裂隙的转化。当裂隙面曲率较大时,式(12,14)联立时需要谨慎处理渗透率κf,因为渗透率的左散度影响较大,材料的非均质性不能忽略不计。

从图5的算例证实有限裂隙的厚度越大,渗透率非均质性引入的误差越小,所以在等效渗透率κfc远大于多孔介质本身渗透率κfp的情况下,应尽量增加有限裂隙的厚度。合理增加网格数量和裂隙面厚度可以减小误差(图6)。然而裂隙厚度增加相当于曲面相对曲率增加,式(18)的系数k随着曲率增加计算误差逐渐增大。综合图5和图6可以看出,网格尺寸越小,有关微分运算的精度越高;在相对有限裂隙厚度(hc/Δl)不变的情况下,有限裂隙厚度越大,物性参数变化越大,非均质性引起的计算误差升高;相对有限裂隙厚度越大,在网格尺寸不变的情况下,物性参数非均质性引入的误差降低,但是在裂隙面曲率的约束下,不能无限制地增加有限裂隙的厚度。

图5 不同厚度有限裂隙的流速大小分布Fig.5 Velocity magnitude distributions for various widths of the finite crack

图6 裂隙内物理量的计算结果Fig.6 Numerical results in the original crack

5 讨 论

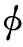
有限裂隙模型可以推广到多孔介质中含宏观孔隙的问题。由于在宏观上看孔隙本身是一条曲线,有限厚度的孔隙则成为轴线为曲线和半径为h的柱体。仿照式(5,6),分别对孔隙度和渗透率使用公式

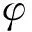
(31)

式中la为孔的轴线。如果圆孔中为层流流动,Darcy定律修改为

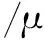
(32)

式中D为圆孔的直径,el为孔隙轴线的切向单位矢量,下标fa为有限孔隙内的流体,a为原始孔隙内的流体。对速度、密度和压强等其他物理量使用公式

(33)

将孔隙内的物理量重新定义在有限厚度的孔隙内。计算完成之后,仿照式(16,17)或式(18)可以求出原始孔隙内的压强和速度。

6 结 论

本文提出了一种双重介质有限裂隙连续介质渗流力学模型。受数学界面和物理界面的启发,该模型将零厚度的裂隙通过定义域延拓看作有限厚度和具有高渗透率的连续介质,并通过质量、动量和总压力等效和控制方程不变的原则,获得有限裂隙的孔隙率和渗透率物性参数、流速和压强等物理量。在网格满足精度要求情况下,有限裂隙面越薄,结果越准确。该模型的使用包含三个步骤,首先将数学裂隙面的各物理量和物性参数等效为有限裂隙模型的物理量和物性参数;然后将等效流场和多孔介质自身的流场耦合,求解得出总体流场的结果;最后将计算结果映射到裂隙面上,得到裂隙内的流速和压强。

该模型的优点在于将二维的裂隙面看作三维的多孔介质实体,使用统一的输运方程描述裂隙-多孔介质耦合的流动,并且该模型可以方便拓展到孔隙-裂隙-多孔介质耦合的流动。这一模型在三维空间求解低维-高维耦合的流动问题,可以应用于不方便在几何上实施高维度-低维度耦合求解的数值计算方法。