基于新息自适应卡尔曼滤波算法的多类型结构响应重构
2023-10-26丁怡渊彭珍瑞
丁怡渊, 殷 红, 彭珍瑞
(兰州交通大学 机电工程学院,兰州 730070)
1 引言
各类结构动态响应的精确度是影响结构健康监测系统性能的关键因素。然而在实际工程中,传感器布置的位置和数量往往会受到经济因素和传感器安装条件的限制,结构上很多位置并未安装传感器,这就会造成监测数据的不完备。因此,利用有限数量传感器测量响应得到结构未测量处响应的结构响应重构技术具有十分重要的研究意义[1]。
目前,针对结构响应重构的研究可依据是否考虑误差分为结构响应重构的确定性方法和不确定性方法。结构响应重构的确定性方法基于准确的有限元模型,建立已测量响应与待重构响应之间的关系,实现对未知响应的重构。具体方法包括基于模态分析[4,5]、传递率或传递矩阵[6,7]、经验模态分解[8]和马尔科夫链[9,10]等。然而获取精确的有限元模型对于复杂的大型结构来说较为困难,并且其结构参数随着服役时间必然有所改变。若有限元模型精度得不到保证,必然会影响确定性方法的重构精度。结构响应重构的不确定性方法不必基于精确的有限元模型,并可以考虑在一定的模型误差和测量误差下重构结构的响应。卡尔曼滤波KF(Kalman filter)算法是一种采用递推形式的时域滤波算法,能够有效地处理模型误差和测量误差,实现对系统状态的最优估计。张笑华等[11]基于KF算法对二维桁架的位移和应变响应进行重构,且发现利用两种信息重构得到的响应比用单种信息重构的结果精度更高。徐幼麟等[12]使用KF对大跨度悬索桥进行应变、位移和加速度响应进行重构,并结合逐步消去法对多类型传感器进行优化布置。
目前大多数基于KF算法的结构响应重构方法,需要预先假定过程噪声方差和测量噪声方差已知且为常数。然而,其大部分情况下是未知且时变的。使用不准确的噪声方差显然是不合理的,可能导致较大误差的状态估计,甚至导致滤波器发散。新息定义为测量估计值与实际测量值之差,其表示存在于测量响应中而滤波器无法预测的那部分信息,可以用于噪声方差的估计。因此,Lai等[13]提出了一种移动窗口扩展卡尔曼滤波算法,通过新息分别估计过程噪声方差和测量噪声方差。Zhang等[14]在此基础上使用移动窗口卡尔曼滤波MWKF(moving-window Kalman filter)算法对一简支梁的应变和位移响应进行了重构,验证了此方法在多类型响应重构中的有效性,但上述方法均需要利用经验选取移动窗口的大小。张志勇等[15]根据新息统计特性结合扩展卡尔曼滤波算法,提出一种增益和状态估计误差协方差矩阵的自适应调整策略,但该方法并未对测量噪声方差进行实时的估计。
基于以上背景,针对噪声方差无法准确获得而导致KF滤波器性能降低,进而造成响应重构精度低的问题,研究有限测点下基于新息自适应卡尔曼滤波IAKF(innovation adaptive Kalman filter)算法的多类型结构响应重构。首先,通过新息的理论协方差矩阵和实际协方差矩阵计算得到调整因子,利用调整因子对卡尔曼滤波增益和状态估计误差协方差矩阵进行实时自适应调整。然后,利用有限测点的加速度响应,结合模态法对结构各处的加速度、速度、位移和应变响应进行重构。最后,对起重机桁架和简支梁分别进行数值模拟和试验分析,验证了所提方法的有效性和可行性。
2 理论基础
2.1 结构运动状态空间方程
线性系统的结构动力学方程可写成连续的状态空间方程。由于实测数据都是离散的,且存在反映建模误差的过程噪声和反映传感器以及外界误差的测量噪声,则连续的状态空间方程经过离散后,可得到离散时间随机状态空间为
(1)
式中各项具体表示为
(2)
(3)
(4)
(5)
(6)
式中下标k为第k时刻,x,y和u分别为离散后的状态向量、观测向量和外部激励向量,q为模态坐标向量,A和B分别为离散化后的状态矩阵和输入矩阵,C和D分别为输出矩阵和直接传输矩阵,Δt为采样时间间隔,I为单位矩阵,w和v分别是过程噪声向量和测量噪声向量,w和v假定为均值为零且互不相关的高斯白噪声,其方差矩阵分别为Q和R,ξ为阻尼矩阵,ω0为模态频率矩阵,L为激励映射矩阵,Φ为模态位移振型矩阵,T为应变位移转换矩阵。
2.2 卡尔曼滤波算法
卡尔曼滤波算法是一种利用线性系统状态方程,通过观测数据对系统状态进行最优估计的算法。该算法一般包括先验和后验两个部分,即预测和更新。其中预测即先验状态估计和先验估计误差协方差;更新即结合先验状态估计和卡尔曼增益计算得到后验状态估计和后验估计误差协方差,
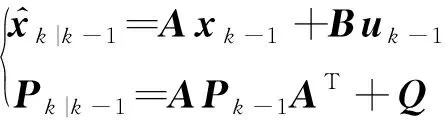
(7)
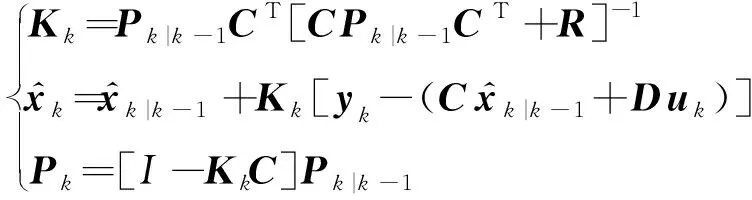
(8)
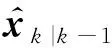
2.3 移动窗口卡尔曼滤波算法
在结构响应重构中,过程噪声主要包括有限元建模误差,测量噪声主要包括传感器测量误差以及外界环境噪声。传统KF算法中Q和R通常需要凭经验评估,且常假定为恒定的常数。然而在实际工程中,Q和R通常是时变的。文献[14]首次引入MWKF算法对测量噪声方差进行估计,由于在响应重构过程中真实的测量响应难以获得,从而各个时刻真实的测量噪声vk无法估计,故采用前一时刻、当前时刻和后一时刻这三个时刻的权值相加作为当前时刻的真实响应,
(9)
式中λi为加权系数(i=1,2,3,λ1+λ2+λ3=1),上标r为真实值,上标m为测量值。测量噪声可表示为
(10)
通过测量噪声vk结合移动窗口法得到测量噪声的均值E[vk]和测量噪声方差Rk为
(11)
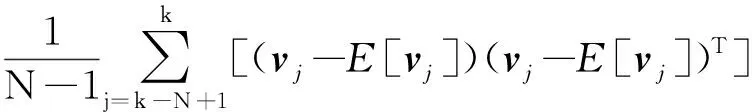
(12)
式中N为移动窗口长度,即统计样本个数。
对选取不同移动窗口得到的Rk进行加权平均处理得到最终的测量噪声方差,
(13)
式中σi为加权系数。
2.4 新息自适应卡尔曼滤波算法
在上述MWKF算法中,假设真实的测量响应是通过三个时刻的响应加权得到的,而加权系数λi需要通过经验选取,存在不确定性。由于新息反映测量值与估计值的差异,所以可以通过新息序列对噪声方差进行自适应调整,从而实现对卡尔曼滤波增益和状态估计误差协方差矩阵进行自适应调整,保证滤波器性能并降低估计误差。因此,本文提出了新息自适应卡尔曼滤波算法,在噪声方差未知的条件下,对R可以进行实时估计。
新息定义为测量值与估计值之间的误差[15]
(14)
新息的理论协方差矩阵可以定义为
(15)
在实际过程中,新息的协方差受建模误差和测量误差的影响,所以新息的实际协方差矩阵为
(16)
式中M为移动窗口的长度。

(17)
式中trace为矩阵的迹。
在更新卡尔曼滤波增益矩阵时,对R进行如下的自适应调整,
Kk=Pk|k-1CT(CPk|k-1CT+αkRk)-1
(18)
为了提高卡尔曼滤波算法的估计精度,测量噪声方差矩阵与过程噪声方差矩阵一般作相反调整[17],在更新先验估计误差协方差矩阵时,对Q进行如下的自适应调整,
Pk|k-1=APk-1AT+Qk-1/αk
(19)
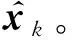
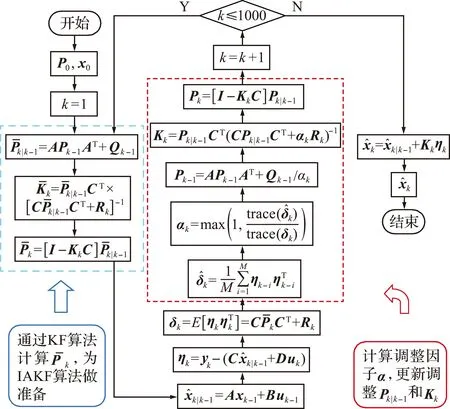
图1 IAKF流程Fig.1 Flow chart of the IAKF

2.5 多类型结构响应重构
由IAKF得到的预测状态向量可以得到测量方程和重构方程,
(20)

为了在相同的条件下对基于KF,MWKF和IAKF这三种算法进行重构效果的比较,使用相对百分比误差RPE(relative percentage error)来衡量重构的精度,
RPE=std(ye-yr)/std(yr)×100%
(21)
式中std为标准差。
3 数值模拟
采用起重机二维桁架来模拟整个响应过程,以验证所提方法的有效性。该桁架结构共有56个单元,30个节点和56个自由度,如图2所示。其弦杆和腹杆截面积分别为2 cm2和3 cm2;弹性模量分别为70 GPa和210 GPa;密度为7850 kg/m3;泊松比为0.3。由于低阶模态更容易受外界激励,其模态振型包含的信息也更重要,而高阶模态对结构响应贡献很小可忽略,因此选取前六阶模态振型为目标模态进行响应重构。在本算例将一白噪声激励施加于30节点的Y方向,激励的频带宽度范围为10 Hz~250 Hz,其最大值为35 N。随机选取11节点Y方向和24节点Y方向,通过式(20)可计算其加速度响应,并加入均值为0、方差为2.56的高斯白噪声作为测量响应。

图2 起重机桁架Fig.2 Crane truss
作为对照,表1列出了在设定不同Q时基于MWKF、KF以及IAKF这三种方法进行重构的各个节点或单元的加速度、速度、位移和应变响应的平均RPE值。由表1可知,当通过经验选取Q1为1×10-14时[18],使用三种重构方法进行响应重构的精度均较高,加速度、速度、位移和应变响应的平均RPE值均在4%以下,而采用IAKF对4种类型响应的重构精度均有较大幅度的提高,平均RPE值均在1%以下;当Q未通过经验调整选取时,即假设Q2和Q3分别取为1×10-13和1×10-12时,采用传统KF算法和MWKF算法由于Q选取不合理而导致其滤波器性能急剧下降,从而严重影响响应重构的精度,而采用IAKF算法仍然可以保证滤波器的性能,且四种类型响应的重构精度几乎没有受到影响,证实了采用新息自适应卡尔曼滤波算法在过程噪声未知情况下进行响应重构的有效性,且在过程噪声未知的实际工程结构中具有重要现实意义。

表1 不同过程噪声协方差Q下的平均RPE值Tab.1 Average values of the RPE under different process covariance Q
图3为11节点Y方向的测量噪声方差时程曲线。可以看出,使用IAKF算法估计的测量噪声方差在整个过程中随着时间推移不断变化,且围绕预设的真实值上下波动,证实使用IAKF算法估计的测量噪声方差都趋于预设值,可用于后续的响应重构计算。

图3 传感器测量噪声方差Fig.3 Measurement noise variance of the sensor
图4为结构各处的重构响应与计算响应对比,采用IAKF进行响应重构的各类响应时程曲线与计算响应时程曲线吻合良好,可以用于过程噪声和测量噪声方差未知情况下的响应重构。
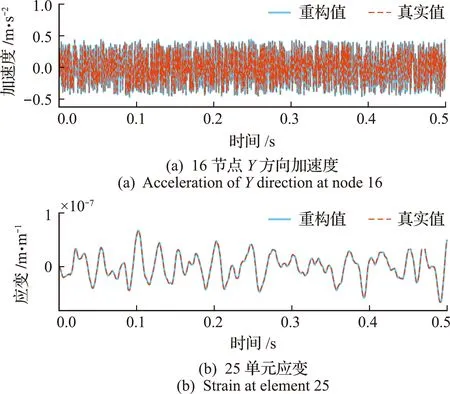
图4 重构响应与计算响应对比Fig.4 Comparison of reconstructed and computed responses
图5为所有56个自由度的加速度和位移响应重构的RPE值。可以看出,基于KF算法和MWKF算法进行加速度响应重构时,在个别自由度的响应重构精度较低,基于KF算法重构响应的RPE值在部分自由度甚至超过8%,基于MWKF算法重构响应的RPE值在部分自由度超过了5%。而基于IAKF算法在进行响应重构时对所有自由度重构精度较高,其RPE值均在2%以下。证明IAKF算法对多自由度结构进行响应重构更具优势。
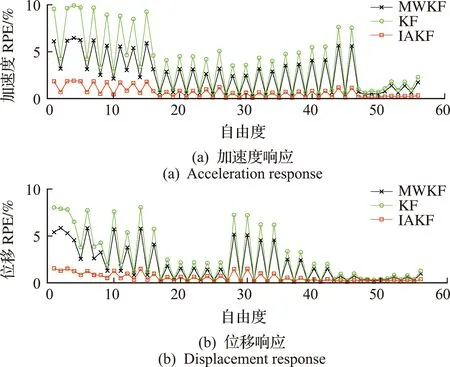
图5 所有节点各类响应的RPE值Fig.5 RPE of various responses at all nodes
为了探究在传感器位置发生改变时,基于IAKF的结构响应重构精度是否下降,即对测点的随机变化是否具有一定的鲁棒性。将测量位置改为另外两组进行对比,第一组选取22节点Y方向和30节点Y方向加速度响应,第二组选取17节点Y方向和25节点Y方向加速度响应。再次进行响应重构并对比重构精度。由表2可知,更改测点后此方法仍能较好地重构其他位置的响应,对比各类重构响应的平均RPE值,重构精度并未发生较大变化,验证了所提方法的鲁棒性。

表2 平均RPE值Tab.2 Average values of the RPE
4 试验分析
为了进一步验证所提方法的有效性,采用简支梁作为试验对象来进行试验验证。其传感器布置如图6所示,梁长2000 mm,宽100 mm,厚10 mm,弹性模量为128 GPa,材料的密度为6440 kg/m3,泊松比为0.3。将简支梁划分为20个单元,21个节点和19个自由度。选取前6阶模态振型作为目标模态进行响应重构。简支梁以及实验设备实物如图7所示,采用型号为INV9821的加速度传感器来实时记录结构的加速度响应,采用500 kg力锤进行模态试验,采用5000 kg力锤对结构进行激励;采集仪型号为INV3062-C2;采样频率为4000 Hz,采样长度设为4096。对11节点的Y方向施加锤击激励,激励的最大值为10.8 N。在第9和第13节点位置分别布置1个加速度传感器测量其加速度响应作为测量响应值,在第5节点和第17节点位置Y方向布置传感器作对比以检验重构效果,并采用频域积分法[19]将测得加速度响应转换为速度响应和位移响应。表3列出前6阶的模态频率值以及振型的MAC(modal assurance criterion)值,可知频率测量值与Workbench计算值相比,最大误差为1.35%,其余误差基本都低于或接近于1%。且前6阶模态振型的MAC值均近似于1,表明建立的有限元模型与实际试验模型的动力学特性具有很高的相似度,即有限元模型可以预测实际结构的动力学特性,因此可以不对有限元模型进行模型修正。

图6 传感器位置布置Fig.6 Sensor location layout

图7 简支梁试验实物Fig.7 Simply supported beam test object
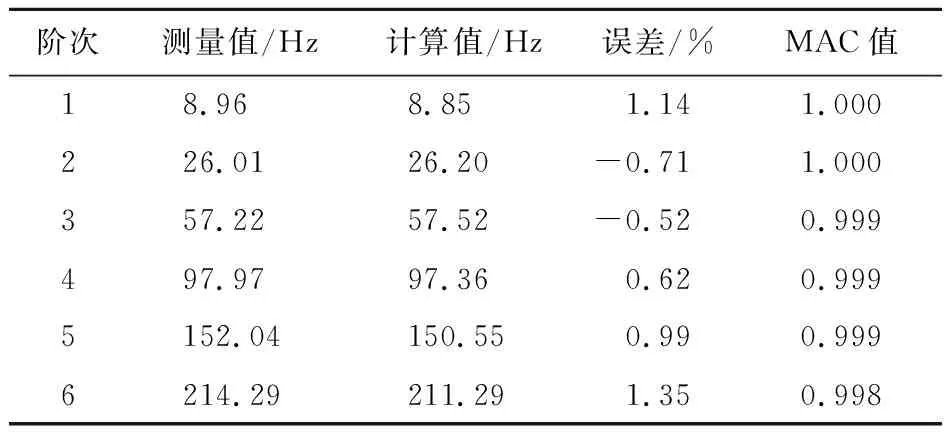
表3 前6阶频率值及MAC值Tab.3 First 6 order frequency and MAC values
基于MWKF和IAKF算法分别对简支梁5节点和17节点Y方向的加速度、速度、位移和应变响应进行重构,图8为分别采用两种方法的重构响应时程和测量响应时程对比,可以看出,这两种方法重构的响应曲线均能与测量响应曲线较好地吻合,证实了所提方法在噪声方差未知的情况下,仅使用加速度传感器可以对其他位置的加速度、速度、位移以及应变响应进行重构,均能得到比较理想的重构结果。
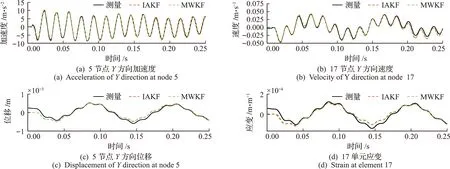
图8 重构响应与测量响应对比Fig.8 Comparison of reconstructed and measured responses
需要指出的是,频域积分法对均值非零的信号进行积分时会在初始值上产生偏差,由于采集得到的加速度数据是离散的,其均值并不能严格等于采样区间连续信号的均值,从而导致重构的位移响应与积分得到的位移响应在初始部分存在较大的误差,这一问题还未得到很好解决。
5 结 论
本文提出采用IAKF算法进行多类型响应重构,用起重机桁架的数值算例和简支梁试验案例验证了方法的可行性,得出以下结论。
(1) 在噪声方差未知,且仅测得部分节点加速度响应时,基于IAKF算法进行响应重构可以对结构其他位置的加速度、速度、位移以及应变响应信息进行重构,各类重构响应时程与计算响应或测量响应时程曲线可以较好地拟合。
(2) 相比基于MWKF算法进行响应重构,IAKF算法避免了权值λ经验选取导致的不确定性,并可以有效地实时调整过程噪声方差,算法中在Q设定不合理的情况下仍然可以保证重构精度。
(3) IAKF算法可以对测量噪声方差进行实时估计,估计结果与预设值误差较小,与固定的测量噪声方差相比,采用时变的测量噪声方差更符合工程实际。
由于卡尔曼类滤波算法基于高斯模型推导而来,故系统噪声和测量噪声需限制为高斯白噪声,作者目前也正在研究基于粒子滤波PF(particle filter)算法响应重构的研究,该方法对噪声没有任何限制,相比于KF类算法具有独特优势。
