化归思想在解方程（组）教学中的应用

王志宇 苗凤华

【摘要】随着课程改革，在数学课程和教学中渗透一些数学思想方法越来越重要，其中化归思想是数学中重要的数学思想方法之一，在数学知识学习和数学解题中都经常用到.初中数学解方程（组）教学主要包括：一元一次方程、二元一次方程组、可化为一元一次方程的分式方程.尽管每类方程（组）的解法不尽相同，但是归根结底是利用化归的基本思想将方程（组）转化为最基本的一元一次方程的问题，文章主要介绍化归思想在这些内容中的应用.

【关键词】化归思想；二元一次方程组；一元二次方程；分式方程

一、历史上的化归思想应用综述

化归思想是数学中常用的数学思想方法，无论在新知学习还是在数学解题中都经常用到.很多著名学者都对化归思想有过比较深入的研究.下面举几个典型的例子.

17世纪，法国数学家笛卡尔发明了解析几何，解析几何实现了用代数的方法研究几何问题，按照他的观点，所有问题都可化归为数学问题，进而可化归为代数问题，最终化归为解方程的问题.笛卡尔建立的平面直角坐标系，成功实现了几何问题向代数问题的转化.

古希臘数学家欧几里得著的《几何原本》是古希腊数学的代表作，这本书构建了几何公理化体系.将众多几何命题的证明都归结为最基本的定义、公设和公理，几何公理化体系是化归思想的典型应用.

我国古代著名的《九章算术》在历史上有着非常重要的价值.书中的每一个题目都由“问、答、术”组成.“术”即解决问题的方法.书中很多解决问题的方法都体现了化归思想.此外，很多问题都是将实际生活中的问题转化为数学问题.这种将生活中的实际问题转化成数学问题的过程充分体现了化归的数学思想.

二、化归思想的概念

化归思想是指在解决数学问题时通过变换条件使之转化，进而解决问题的一种方法，即转化和归结.它是一种非常重要的数学思想方法，化归思想往往能够将一些未知的、复杂的问题，转化为已知的、简单的问题，并使之得到解决.

三、解方程（组）教学中出现的一些问题

（一）忽视学生主体性

在实际教学中，存在着教学过于注重“基”的落实，而忽视了学生的主体性的问题.解方程（组）作为数学教学中的重点内容，很多教师过于强调基础知识，注重对解方程（组）步骤的归纳，并通过机械训练实现对学生解题的强化，忽视了对数学思想方法的渗透，同时忽视了学生自己去探究的过程，学生仅仅知道“怎么做”而不知道“为什么这样做”，这就难以使学生了解化归思想的作用，难以利用化归思想学习知识.

（二）忽视化归思想渗透

在初中数学方程（组）的实际教学当中，许多教师把教学重点放在归纳解方程的步骤上，忽视了化归思想的渗透，忽略了知识生成的过程，不肯花费时间让学生探索知识的形成过程，抑制了学生的思维，导致其逐渐丧失了学习数学思想方法的欲望.

（三）缺乏精讲精练指导

现在很多初中数学教师在开展方程（组）有关内容的教学讲解和练习时引导学生套用步骤进行机械训练.而精讲精练应该是把讲解重点放在对学生思路的引导：即面对新的知识如何思考，将其转化为已有的知识，并有针对性地进行练习，否则学生只会死板地套用，并不知道知识间存在的内在联系，学生则记忆困难，面对陌生一点的题目就无从下手.

四、化归思想在解方程（组）教学中的应用

方程求解的模式基本为化归为一元一次方程进而化为ax=b（a≠0）的形式进行求解.如二元一次方程组相比一元一次方程，多了一个未知数，在解二元一次方程组时无论是代入消元法还是加减消元法目的都是实现消元，将二元一次方程组转化为一元一次方程的问题；三元一次方程组，是先通过消元的方法化归为二元一次方程组，再化归为一元一次方程的求解问题；可化为一元一次方程的分式方程则通过“去分母”转化为整式方程；一元二次方程则通过“降次”转化为一元一次方程的求解问题.

教师教学前先要对教材内容进行分析，在进行教材分析时就应具有化归意识，找到其中运用的化归方法及其相关联的化归思想，厘清各部分知识之间的化归关系，更好地对教材相关知识进行整体把握.教师通过教材分析，挖掘出教学内容中能够渗透的化归思想，引导学生掌握化归方法，实现化归思想的有效渗透.以华师版初中数学教材为例，方程这一部分知识编排如表1所示.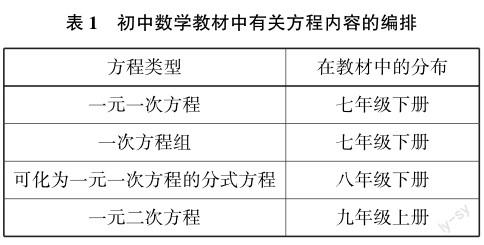

从表1可以看出，虽然不同类型的分布在不同年级的教材中，但是它们之间是存在着一定联系的，如图1所示，各种类型的方程之间存在着化归关系.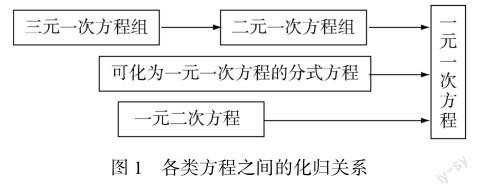

下面对化归思想在几种不同类型的方程中应用的进行举例分析.

（一）化归思想在二元一次方程组教学中的应用

学生在学习解二元一次方程组之前，学习过解一元一次方程，因此，可以通过化归，把“二元”变为“一元”.但是，很多数学教师往往侧重于求解的步骤的教学，忽视了对“化归”思想的渗透.《义务教育数学课程标准（2022年版）》将“能用代入消元和加减消元法解二元一次方程组”变为“能用消元法解二元一次方程组”，这可以看出新课程标准不再限定学生用“哪种消元”，而重点是达到“消元”的目的.如果教师能将化归思想的渗透落到实处，这样学生的分析问题能力、思维能力、逻辑推理能力都会有所增强.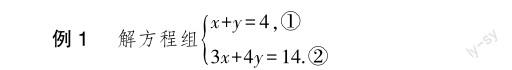

求解这个方程组时，学生通常用常规的代入消元和加减消元得出答案.但是要想让学生深入理解“化归思想”的精髓，教师在教学中可以这样引导学生：

【问题引入】出示二元一次方程组，请同学们思考：方程中有几个未知数？这和我们之前学过的方程有何区别？引导学生想出解决思路———消掉其中一个未知数，将其转化为学过的一元一次方程.

【问题】消掉哪个未知数更好？（引导学生观察方程）

在这个过程中学生能够充分观察思考，体现了学生的主体性.

【归纳】学生会用各种方法找出解题思路.

把x+y看成一个整体，再将方程②变形为3（x+y）+y=14，③

那么将方程①整体代入③，可得3×4+y=14，

这样就非常容易将二元一次方程组转化成了一个一元一次方程问题.

【总结与强化】教师归纳总结：由于整体代入后容易消掉未知数x，所以没有必要按照传统的固定模式去套用.看到一个二元一次方程，要先观察、思考，核心是“消元”，而消元方法是多样的.

这样就实现了对学生学习方法的指导和精讲精练的目的，在具体问题中渗透了化归思想.

（二）化归思想在三元一次方程組教学中的应用

三元一次方程组属于《义务教育数学课程标准（2022年版）》中规定的选学内容，不做考试要求，因此很多教师认为学习三元一次方程组会增加学生负担，但是如果领悟到解三元一次方程组的基本思想———化归为二元一次方程组，即可将复杂问题简单化.而且，消元的方法不是一成不变的，是灵活的，为了让学生意识到这一点，深刻体会转化的思想，可以设计如下的例题.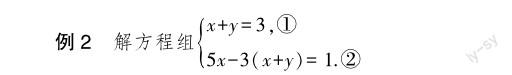

【思路分析】观察后发现方程①的左边是x+y，而方程②的括号里也是x+y，可以把x+y视为一个整体，把方程①直接代入到方程②中，将方程②直接转化为一元一次方程，从而达到“消元”的目的.

这样的设计，可以让学生通过例子体会到通过“整体代入”达到“消元”的目的，很容易地将三元一次方程组的问题转化为简单的二元一次方程组进而转化为解一元一次方程的问题.

（三）化归思想在一元二次方程教学中的应用

对学生而言，一元二次方程的学习难度是比较大的.而一元二次方程根与系数的关系，可以在不解方程也能得到一元二次方程的两根和与两根积的值.因此，它在一些求参数的值以及取值范围时非常适用.此外，有时可以将非一元二次方程的问题转化为一元二次方程，将复杂问题简单化.

学生在完成两个任务时可先进行思考，再进行讨论.

【总结】请同学思考，我们把这个问题化归为了一个什么问题？

这样的教学过程，将复杂的题目转换成为一元二次方程，进而转化为一元二次方程根与系数的关系问题.这样解决了问题的同时让学生有了化归意识，体现了学生学习的主体性以及对学生学习方法的指导.

（四）化归思想在换元法解决方程问题中的应用

中学数学学习的分式方程仅仅局限于可化为一元一次方程的分式方程，对于超出这个范围的分式方程，我们可以通过换元的方法将其转化为学过的方程，实现化归.

换元法就是用一个新的符号将未知式子代替，将复杂问题简化.它可以将不熟悉的问题转换为熟悉的问题，进而提高解题效率.在解一些较复杂的分式方程时，换元的一种常用方法，它还可以起到降次的作用，把高次方程转化为低次方程，这是化归思想的体现.

这个问题能让学生意识到，陌生问题可以通过化归，转化为熟悉的问题.学生通过这个问题的解决进一步理解了化归思想，避免了遇到新问题“束手无策”的情况.

结 语

在解方程（组）的教学当中，化归思想是非常重要的数学思想之一，化归思想可以将复杂的问题转化为简单的问题.让学生抓住核心问题、深刻理解，更好地培养学生的思维.教师在日常教学中，要积极融入化归思想，不断激发学生的探究数学新知的兴趣，提高课堂教学效率.

【参考文献】

[1]钱佩玲，邵光华.数学思想方法与中学数学[M].北京：北京师范大学出版社，1999.

[2]贾应龙.整体思想在解决初中数学一元二次方程中的应用[J].数学学习与研究，2021（10）：36-37.

[3]马艳，马贵.化归思想方法在中学数学教学中的应用———以解方程为例[J].北京教育学院学报（自然科学版），2012，7（03）：1-4.