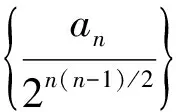构造常数列解决数列中累乘法求通项问题

刘琳琳

(山东省泰安市宁阳县第一中学,山东 泰安 271400)

2022年高考全国Ⅰ卷对数列的考查再次打破了2021年高考的考查模式,回归到独立单一递推关系式,采用了分式型递推关系式,这类试题在求数列通项公式时反复练过,应该是熟题,但考前模拟训练相对较少,所以有部分学生感到不适.

(1)求{an}的通项公式;

本题的主要问题集中在求解数列通项公式上,第(2)问只是一个裂项相消求和问题,比较简单,所以我们主要研究第(1)问.

1 试题求解

解法1(基于项的累乘法)因为a1=1,

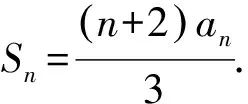
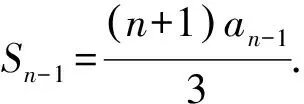
整理,得(n-1)an=(n+1)an-1.

两边同除以n,得

点评解法1是我们平时求数列通项常用的累乘法,根据数列的递推关系求通项公式,目前绝大多数的教学辅导用书上所介绍的方法都是累加法、累乘法、待定系数法等．

解法2是通过构造常数列把一个变化的数列转化为常数求解,这样往往减少很大的计算量,也不必再对a1=1进行检验,达到四两拨千斤的效果．

定义已知数列{an},若an+1=an,则称数列{an}为常数数列.

若数列{an}是常数数列,则an=a1,所以求常数数列的通项公式只要求出首项a1即可．

2 类题研究

类型1An+B,A(n+k)+B是相邻两项,即k=1.

所以(n+1)an+1=nan.

因此{nan}是常数列,所以nan=1×a1=2 .

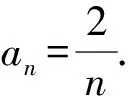
例2 已知数列{an}中,a1=1,(2n+1)an+1=(2n-1)an,求{an}的通项公式.

解析由(2n+1)an+1=(2n-1)an,得{(2n-1)an}是常数列.

所以(2n-1)an=a1=1.

方法小结关注递推关系式中的项,把关于n的两个式子与项对应起来,构建项与项数的乘积或者商的结构形式,形成常数列,直接可以写出数列的通项公式[1].

类型2An+B,A(n+k)+B中的项数k间隔一位.

(2n+1)an=(2n-3)an-1(n≥2).

两边同时乘以2n-1,得

(2n-1)(2n+1)an=(2n-1)(2n-3)an-1(n≥2).

故{(2n-1)(2n+1)an}是常数列.

故(2n-1)(2n+1)an=1×3a1=1.

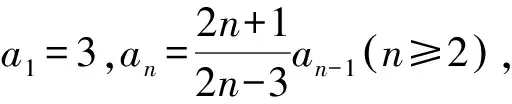
两边同时除以2n-1,得

可得an=(2n-1)(2n+1)=4n2-1．

方法小结变形递推关系式,两边同乘或同除以某个项数,直接构造常数列,从而求出{an}的通项公式,这样操作往往比累乘法更简单,仅仅需要关注递推关系式的结构特点．

以上两种情形都是以构建常数列为基准,相对于累乘法还是要简单些,至于项数相隔再多的递推关系,一般不会出现,也就没有研究的必要了.

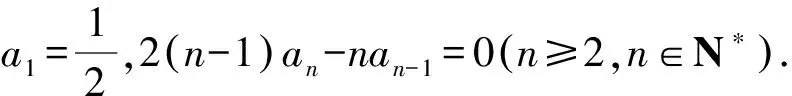
解法1(累乘法)当n≥2时,2(n-1)an-nan-1=0,则2(n-1)an=nan-1.

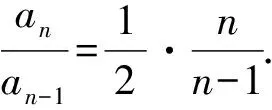
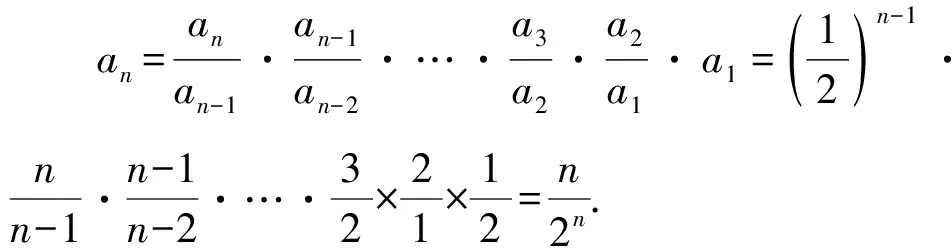
n=1也满足上式,

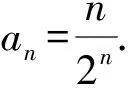
解法2(构造等比数列)由2(n-1)an-nan-1=0(n≥2),得2(n-1)an=nan-1(n≥2).

把以上n-1个式子相乘,得

两边同乘以n+1,得

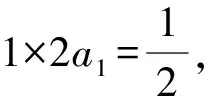
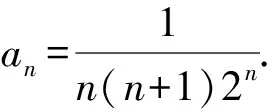
例7在数列{an}中,a1=2,(n2+1)an+1=2(n2-2n+2)an,求数列{an}的通项公式．

解法1(累乘法)依题意,a1=2,(n2+1)an+1=2(n2-2n+2)an.

即(n2+1)an+1=2[(n-1)2+1]an,

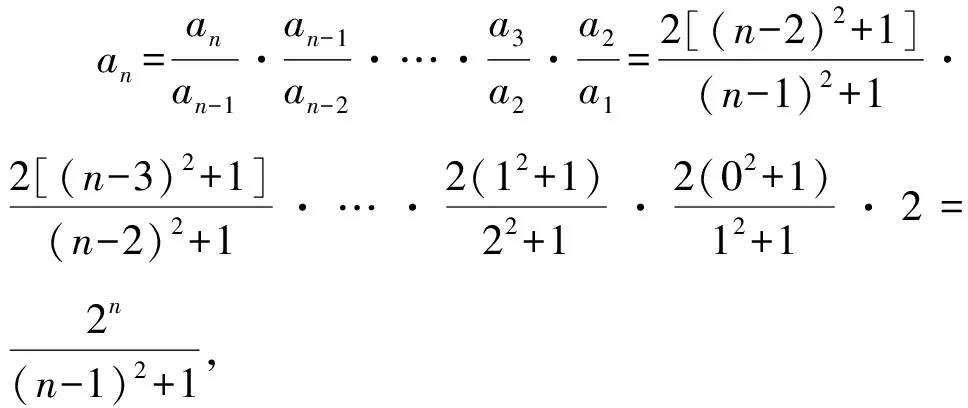
当n=1时也满足上式,

解法2(构造等比数列)由(n2+1)an+1=2(n2-2n+2)an,

配方得(n2+1)an+1=2[(n-1)2+1]an.

所以{[(n-1)2+1]an}是等比数列,首项为2,公比q=2,得

[(n-1)2+1]an=2n.

3 其它形式累乘法

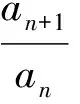
例8在数列{an}中,a1=1,an+1=2nan,求数列{an}的通项公式．

解法2(构造常数列 )因为an+1=2nan,