内螺纹管湍流特性的数值模拟

张定才,马静云,梁 冰,王长通,黄军亚

(1.中原工学院 能源与环境学院,河南 郑州 450007; 2.中原工学院 学报编辑部,河南 郑州 450007)

换热器作为一种重要的热传导和流体传输装置,在化工、能源和航空航天等领域得到了广泛应用[1]。换热器性能对工业生产的影响很大,故提高其效率、强化其传热及探索强化传热的新技术已成为研究的焦点。提高换热器性能,有利于实现能源的高效利用。目前换热器中大量采用的内螺纹管,因具有换热效率高、结构紧凑和成本低廉等优点而受到了广泛关注。受内螺纹管复杂结构影响的非线性流动特性,是近年来的一个研究热点。随着数值模拟和实验技术的发展,越来越多的学者曾致力于内螺纹管流动阻力与其几何参数之间关系的研究。刘爽等以空气为工质研究内肋管换热和阻力特性的实验结果表明:三维内肋管比光管的强化传热效果显著;不同结构参数的内肋管具有不同的强化传热效果;对内肋管强化传热效果的影响由高到低的内肋管结构参数依次为肋高、肋间距、肋宽[2]。Raj等用乙二醇、水两种流体,通过实验研究了螺纹角、螺纹高度在层流和湍流状态下对内螺纹管传热性能的影响[3]。其研究结果表明:在层流状态下,以乙二醇作为流体时管内表面换热效率可增强 34%;在湍流状态下,以水作为流体时管内表面换热效率可增强 18%。李隆键等通过实验发现:三维内肋对内螺旋管的对流换热效果具有较大的强化作用,同时流阻也有一定程度的增加;在测试的雷诺数范围内,与光管相比,所用内螺旋管的平均传热强化比为1.27～2.0[4]。李占锋等通过数值模拟得出:螺旋槽管在湍流工况下的平均努赛尔数Nu大约是光管的1.6～2.1倍,平均阻力系数大约是光管的1.5～4.0倍[5]。孙东亮等通过数值模拟得出:在层流状态下增大螺旋角,能够在很大程度上提高换热能力;增大肋条数也可以提高换热能力,但提高程度较小[6]。靳遵龙等采用CFD技术的研究发现:适当减小螺距可有效提高对流侧换热能力;随着肋高的增加,换热性能会得到改善,且摩擦系数增加的比例与肋高增加的比例大致相同[7]。陈嘉璐通过数值模拟研究内凸式螺纹管的管程流动和传热过程,并分析了流体雷诺数、螺纹管肋高和螺纹间距对流体流动的影响[8]。李论通过模拟研究发现,在流体流入含肋段时,肋的迎流面和背流面均能通过诱导产生涡流,从而达到强化传热的效果[9]。杨晶通过数值模拟对不同几何参数内螺纹管的研究表明,肋高对换热与流动的影响最大,其次是内螺旋角,影响最小的是螺纹肋条数[10]。

本文将通过数值模拟研究内螺纹管的螺旋角、流速、肋高和肋条数等参数对其阻力特性的影响,并探讨其物理机制,为内螺纹管的优化设计和应用提供参考。

1 物理模型及数学模型

1.1 物理模型

本文主要研究目前应用广泛的梯形肋内螺纹管(见图1)。内螺纹管的重要参数有螺纹肋条数Ns、螺纹肋高度(可简称肋高)e和螺旋角α。

图1 梯形肋内螺纹管示意图

1.2 数学模型

针对流体流动的Navier-Stokes方程,可假定:流体物性为常数;管内流动是定常的充分发展湍流;不考虑流体中的质量力;管壁温度为常数。

2 离散方法及数值方法

2.1 离散方法

采用微分方程法生成适体坐标网格,令内螺纹管的e=0.30 mm,Ns=20,α=25°;在其边界附近划分出4种典型的区域,即拐角处的肋间区域a、与之相邻的肋顶区域b、其他肋间区域c、其他肋顶区域d,且除区域a外使所有网格均匀分布;针对区域a,b,c,d,e,分别利用Poisson方程法生成网格,并采用Thomas/Middlecoeff方法来控制网格;在来流方向 (x方向)上选取螺纹肋扭转角度γ为1°的轴向长度,作为1个轴向控制容积。这里,适体坐标系下计算空间的每个方向上控制容积均为1个单位长度。本文划分的内螺纹管横截面网格和三维网格如图2所示。

(a) 横截面网格 (b) 三维网格

在使用有限体积法建立离散方程时,可通过节点物理量的插值求出控制体积界面上的物理量及其导数。引入插值法是为了建立离散方程,不同的插值方式对应于不同的离散结果。

采用离散方法计算时,应尽量选用具有较高精度和稳定性且能适应不同流动形式的离散格式。但实际上,理想的离散格式是不存在的,即没有普遍适用的既稳定又准确的离散格式,应根据实际问题选择不同的离散格式。参考相关文献并通过计算比较,本文针对流项采用二阶迎风格式。

2.2 数值方法

对于进出口为周期性边界条件的内螺纹管,根据充分发展流动及所计算内螺纹管的特点可知,由横截面上同一个网格扭转而来的沿程所有网格上的物理量具有下列特点:标量相等;矢量的模相等,但方向随相对位置而变。由此可列出下列式子:

(1)

式中,Θ(x,y,z)为无量纲温度。其定义为:

Θ(x,y,z)=(T(x,y,z)-Tw)/(Tb(x)-Tw)

(2)

管道壁面的边界条件为:

(3)

2.3 网格独立性验证

表1 5套网格数下平均努赛尔数Nu和阻力系数fRe0.25的计算结果

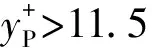
3 雷诺数与肋条数对流动阻力的影响

3.1 雷诺数对流动阻力的影响

在内螺纹管的肋高e=0.30 mm、螺旋角α=35°时,雷诺数变化对单位管长压降的影响如图3所示。

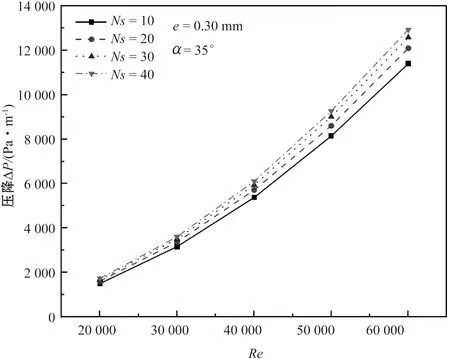
图3 雷诺数变化对单位管长压降的影响

从图3可以看出,随着雷诺数的增加,单位管长压降呈现逐渐增大的趋势,而在雷诺数较大的情况下,这种趋势更为明显。可以说,雷诺数对单位管长压降的影响很大。此外,对比不同肋条数下的单位管长压降变化趋势后发现,它们的增长趋势基本相同。流体在管道内流动时,管道壁面的摩擦力和流体的惯性力是影响流动阻力的两个主要因素。当雷诺数较小时,黏性力作用占主导地位,流体黏附于管道壁面,流体的速度分布较为均匀,流动状态相对稳定,流动阻力较小。但是,当雷诺数增大时,流体的惯性力逐渐增大,流体的速度分布变得不规则,流动状态变得不稳定,从而会增大流动阻力。

为方便与光管Blasius公式(fRe0.25=0.316 4)比较,这里定义fRe0.25为阻力因子。在内螺纹管的肋高e=0.30 mm,肋条数Ns=10、20、30、40时,不同螺旋角的内螺纹管阻力因子随雷诺数的变化如图4所示。

(a) Ns=10 (b) Ns=20

从图4可以看出,随着雷诺数的增大,阻力因子呈现增大趋势,但阻力系数曲线呈现不断降低的趋势。这是由于湍流边界层随雷诺数的增大而逐渐变薄,摩擦阻力会不断减小。在内螺纹管中,边界层变薄使得管内流体在径向的受扰程度降低,从而导致了阻力系数的减小。此外,螺旋角α的增大能增强肋条附近的流体旋转程度,诱发并增强管壁附近的二次流,从而增强对流体的扰动,并产生更大的阻力。内螺纹管中存在湍流时,阻力系数随雷诺数的增大而减小,这与层流下阻力随雷诺数的变化趋势相同。在层流状态下,由于雷诺数较小,黏性效应占主导,流体不易发生扰动。无论是在层流还是在湍流状态下,流动摩擦阻力都会随雷诺数的增大而减小,且高雷诺数下更薄的边界层会导致流场径向扰动的减弱,从而会减小阻力系数。需要指出的是:湍流状态下边界层更薄,流动分离现象仅发生在肋条附近,且总阻力仍以摩擦阻力为主,导致湍流状态与层流状态的阻力系数变化趋势相同。结合压降的分析可知,尽管阻力系数曲线随雷诺数的增大呈现下降趋势,但压降曲线仍呈现上升趋势。

3.2 肋条数对流动阻力的影响

内螺纹管肋条数的增加,意味着管的表面积增大,因此其摩擦效应会略有增强。在较小的雷诺数下,肋条数对压降的影响很小,且随着肋条数的增加,因内螺纹管表面积的增大,单位管长压降会略有增大。在较大的雷诺数下,随着肋条数的增加,压降会明显增大。但是,增加肋条数,由内螺纹管表面积增大引起流体扰动增强的作用很小,导致单位管长压降的变化较小。因此,内螺纹管的肋条数对单位管长压降的影响较小。

与相同半径的光滑管道相比,内螺纹管与流体接触的表面积较大,且随着肋条数增加,该表面积会进一步增大。因此,有必要进一步研究湍流状态下,阻力系数随肋条数的变化趋势。4种螺旋角下内螺纹管肋条数变化对阻力因子的影响如图5所示。

(a) α=15° (b) α=25°

从图5可以看出,阻力系数随着肋条数的增大而增大。这是由于肋条数增大,内螺纹管表面积会增大,使得湍流边界层产生了较大的摩擦阻力。相比于层流,湍流边界层中摩擦阻力随肋条数的变化更大,壁面的剪切应力也更大。这尽管未对流体产生更强的扰动,但是会额外增加摩擦阻力。在层流状态下,内螺纹管表面积增大,对流体扰动增强的作用很小,无法增强内螺纹管的换热效应,导致其总的阻力系数变化不大。

4 肋高与螺旋角对流动阻力的影响

4.1 肋高对流动阻力的影响

内螺纹管肋高的增加对流体流动的影响主要体现在:流体受到的扰动增强;流道内更容易产生二次流;流动混合作用增强。当流体在内螺纹管内流动时,肋高的变化对流体流动速度分布、摩擦阻力和压降等都有着重要的影响。肋高的增加会导致流体流动速度的不均匀分布,使流体在肋条上方的流动速度增大,而在肋条两侧的流动速度减小。这是由于肋高的增加会导致流体的流线发生弯曲,使流体在肋条上方受到剪切力和强制升力的作用,造成流体流动速度分布的变化。这种流动速度的不均匀分布会增大内螺纹管的摩擦阻力,使流动阻力增大。同时,肋高的增加会导致流体与管道壁面之间的距离变小,使内螺纹管的摩擦阻力增大。此外,肋高的增加会导致局部高速流动和局部低速流动现象的发生,从而造成局部的压力损失。这种局部压力损失会增大内螺纹管总的阻力。

本文先后研究了在雷诺数一定、螺旋角一定的条件下,内螺纹管阻力因子随肋高的变化(见图6)。

(a) 雷诺数一定(Re=40 000) (b) 螺旋角一定(α=25°)

从图6可以看出:在雷诺数一定的条件下,随着肋高的增加,阻力因子呈线性增加趋势;在螺旋角一定的条件下,随着肋高的增加,阻力系数也呈线性增加趋势;相比而言,同样是线性增加趋势,但雷诺数大于螺旋角对阻力系数的影响。

分析可知,肋高增大会导致肋条附近流体局部的分离更容易,从而在肋条间引起二次涡,而这种二次涡会增大阻力系数。

4.2 螺旋角对流动阻力的影响

螺旋角描述了肋条的横向倾斜程度,即肋条的旋转程度。随着肋条旋转程度的增大,流体的径向受扰强度增强,会进一步对流动阻力产生影响。当内螺纹管肋高e=0.30 mm、肋条数Ns=40时,在不同雷诺数下螺旋角对单位管长压降的影响如图7所示。

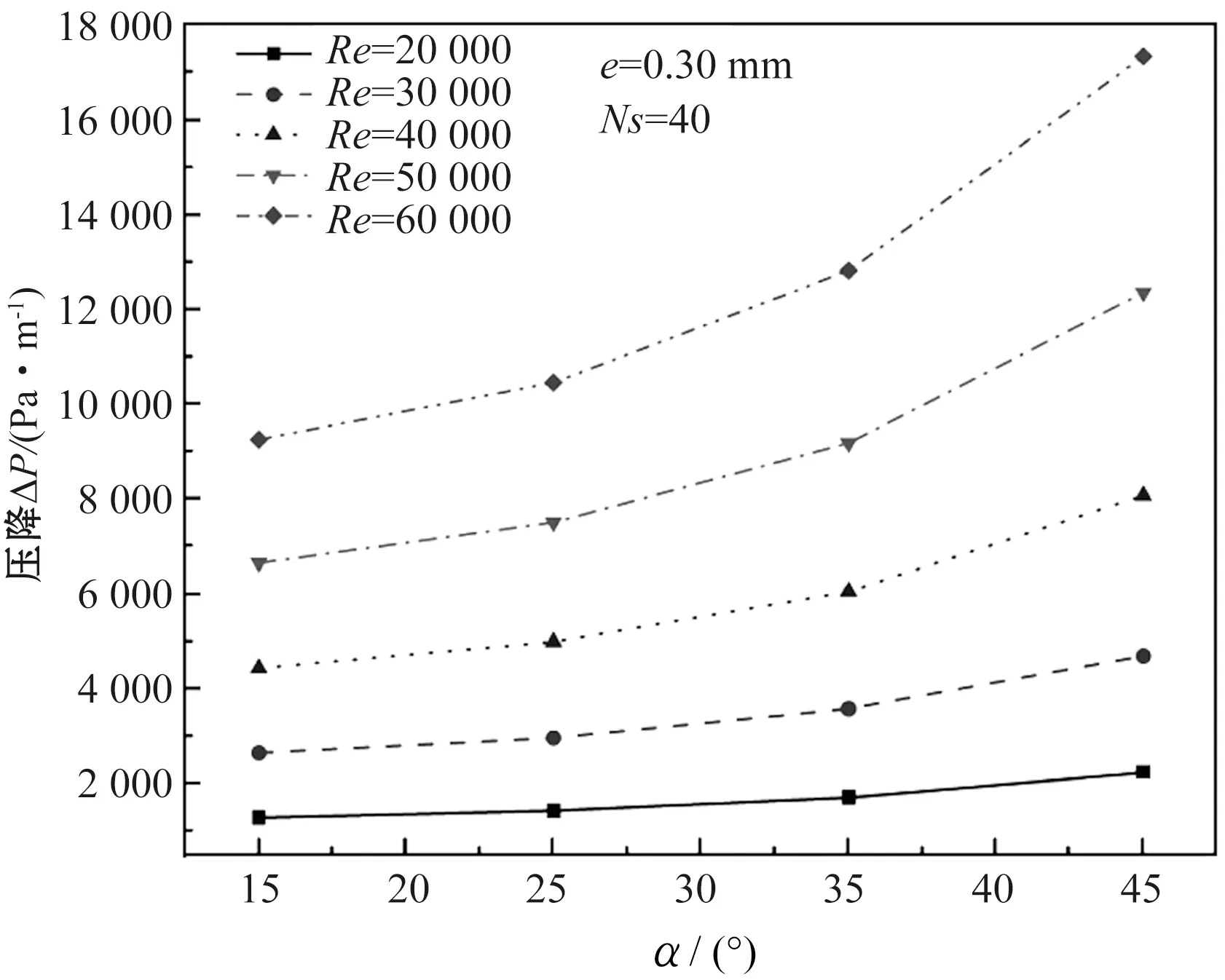
图7 不同雷诺数下螺旋角对单位管长压降的影响

从图7可以看出:随着螺旋角的增大,单位管长压降逐渐增大;随着雷诺数的增大,螺旋角增大导致单位管长压降增大的程度会增加;在较低雷诺数下,增大螺旋角对单位管长压降没有太大的影响。值得注意的是,对于不同的肋条数来说,单位管长压降的变化趋势基本一致。

分析可知,螺旋角对内螺纹管流动阻力的影响主要体现在两方面:一是影响流体流动速度分布的均匀性,使流体的流动速度分布不再是均匀状态,而是在肋条上方随着螺旋角的增大而增大,在肋条两侧随着螺旋角的增大而减小;二是影响流体的湍流程度,当螺旋角增大时,流体在内螺纹管内流动时会发生剪切作用而形成不规则的涡流,从而增大流体的湍流强度。若流体流动速度分布不均匀,则会导致内螺纹管摩擦阻力的增大,从而增大流动阻力。此外,湍流强度的增大也会导致内螺纹管摩擦阻力的增大,从而增大内螺纹管的总体阻力。4种肋条数下内螺纹管螺旋角变化对阻力因子的影响如图8所示。

(a) Ns=10 (b) Ns=20

从图8可以看出,随着螺旋角的增大,阻力系数会逐步增大,且具有较明显的变化趋势。螺旋角增大,表明肋条对流体的径向扰动增强,同时在流动方向上产生了更大的阻滞作用,使边界层的扰动更大。这一变化能够增强流体的混合作用甚至产生二次流,使得换热效果增强,阻力系数增大。从研究结果来看,在螺旋角为45°以下时,阻力系数随螺旋角的增大是单调增加的。这不同于层流中阻力系数存在峰值的情况,也说明了内螺纹管湍流流动与层流流动之间存在的差异。

5 结论

通过模拟分析,在流动参数和管道结构参数变化时,可以获得一些流体流动阻力变化的结论。

(1) 随着雷诺数的增大,单位管长压降呈增大趋势,且雷诺数越大,单位管长压降越大,流动阻力也越大;随着螺旋角的增大,流动阻力会增大;随着肋高的增大,单位管长压降呈线性增长趋势,且增长率随雷诺数的增大而增大;肋条数对内螺纹管流动阻力的影响不像其他参数的影响那样显著,但在更高的雷诺数下,单位管长压降会随着肋条数的增大有一定程度的增大。

(2) 随着雷诺数增大,阻力系数呈现下降趋势,且下降速率随雷诺数的增大而减小;随内螺纹管肋条数的增加,阻力系数会增长,且增长率随着肋条数的增大会出现先增长后减小的趋势,当肋条数在16-20之间变化时,阻力系数的增长率达到峰值;阻力系数随肋高的增大呈线性增长趋势,且相同条件下改变螺旋角对随肋高变化的阻力系数影响不大;随着螺旋角的增大,阻力系数呈指数增长趋势,且在其他条件相同时,若雷诺数越大则阻力系数增长的程度越大。