高速永磁电机三段式转子模态分析与实验验证

胡洪益,晏才松,曾 纯,金海善

(湖南中车尚驱电气有限公司,株洲 412001)

0 引 言

高速电机相比传统电机,不需要中间传动装置,可直接驱动高速负载,具有效率高、可靠性高、体积小、噪声低、维护少等优点,被广泛应用于制冷、制药、氢能源以及污水处理等领域,具有广阔的应用前景[1]。转子设计是高速永磁电机设计的核心内容之一,需要综合考虑电磁、强度以及转子动力学特性要求[2]。其中转子动力学是高速电机转子设计的核心,是保证电机在高速时稳定运行的关键因素。

高速永磁电机转子通常有三种结构:第一种是内嵌式结构,转子铁心通过硅钢片叠压而成,永磁体插入硅钢片设计的磁钢槽中;第二种是表贴式结构,瓦片式永磁体粘贴于轴的表面,永磁体靠过盈配合的碳纤维或合金护套保护;第三种是三段式结构,圆柱或圆环形永磁体与两段轴用胶粘接一体,外圆过盈热套高强度合金护套进行保护固定。三种转子结构不一样,转子动力学建模方法也不一样,而建模会影响计算的准确性。为了准确预测转子的临界转速,可以通过转子模态实验来修正转子动力学模型从而使得转子动力学分析结果更准确。文献[3-4]以表贴式转子为研究对象,建立转子三维模型进行模态仿真分析并通过实验验证。文献[5]以内嵌式转子为研究对象,建立转子三维模型进行模态仿真分析并通过实验验证。而三段式转子建模仿真的研究目前较少,其建模方法的准确性还有待验证。

本文对某磁悬浮高速电机三段式转子进行研究,建立转子三维模型,用有限元仿真软件分析得到固有频率仿真值,然后用锤击法模态实验得到固有频率实验值,两者对比验证了建模方法的合理可行,为三段式转子电机设计以及动力学分析提供参考。

1 转子模态分析

1.1 转子建模

高速永磁电机转子在实际运行时受到轴承支承、单边磁拉力以及负载等多种约束,边界条件复杂,仿真分析很难模拟实际工况。下面简化边界条件对转子做自由模态分析[6],即忽略轴承支撑、单边磁拉力以及负载等约束,减少变量,更直观地验证转子建模的准确性。自由模态仿真得到转子的固有频率,为电机的转子动力学分析提供参考。

以某电机三段式转子为例,该电机采用磁悬浮轴承,用于驱动离心空气压缩机,转子剖面图如图1所示。转子由内部永磁体、两段轴、护套、径向磁轴承、传感器检测环、推力盘以及叶轮、锁紧螺母、拉杆等零件组成。

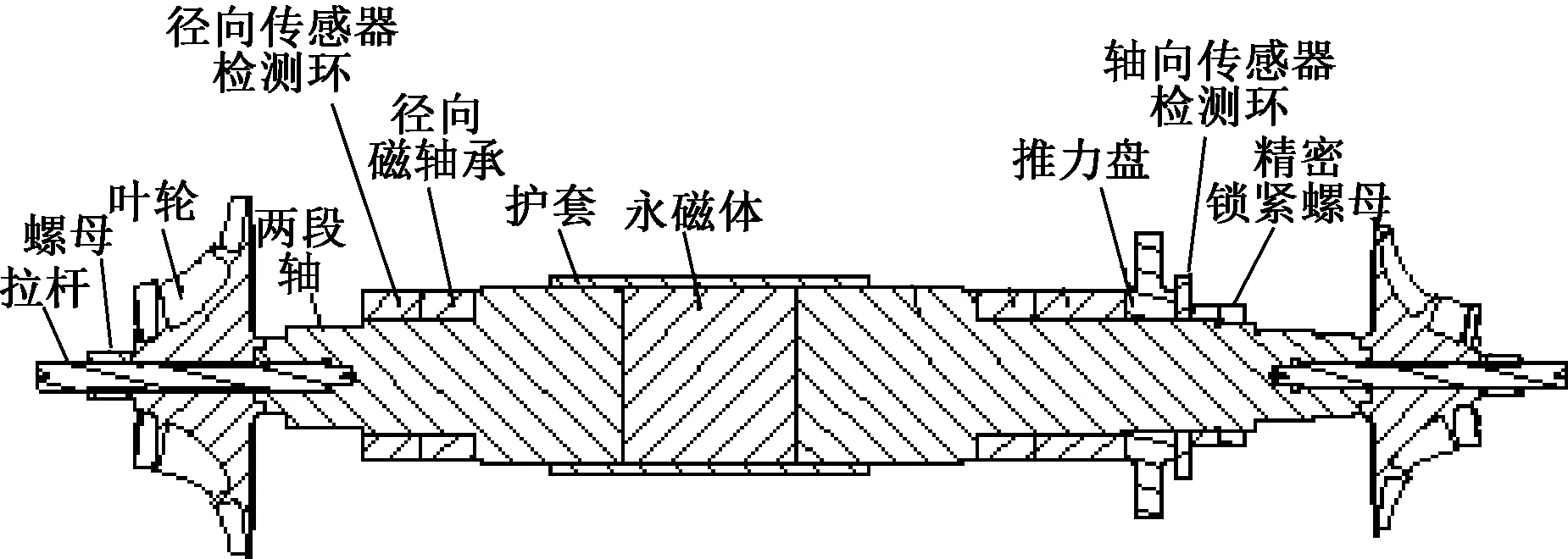
图1 磁悬浮电机转子剖面结构

转子各个零部件的接触关系按如下定义:两段轴端面与磁钢按绑定接触,护套与轴、磁钢过盈配合设置摩擦接触,磁钢弹性模量仅考虑一半。转子轴上的热套的各个零部件材料均需要考虑正交异性,即轴向刚度减弱,横向刚度按材料实际进行设置,接触关系均设置为摩擦接触。电机径向磁悬浮轴承是由0.27 mm厚硅钢片叠压而成,这部分对转子的横向刚度贡献较少,建模按整体建模。轴上其他零部件包括传感器环、推力盘、锁紧螺母、拉杆等均按钢材设置密度,但刚度进行一定程度的削弱。转子装配各零部件材料参数如表1所示,其中材料弹性模量为轴向方向的,因为轴向弹性模量主要影响转子横向振动。

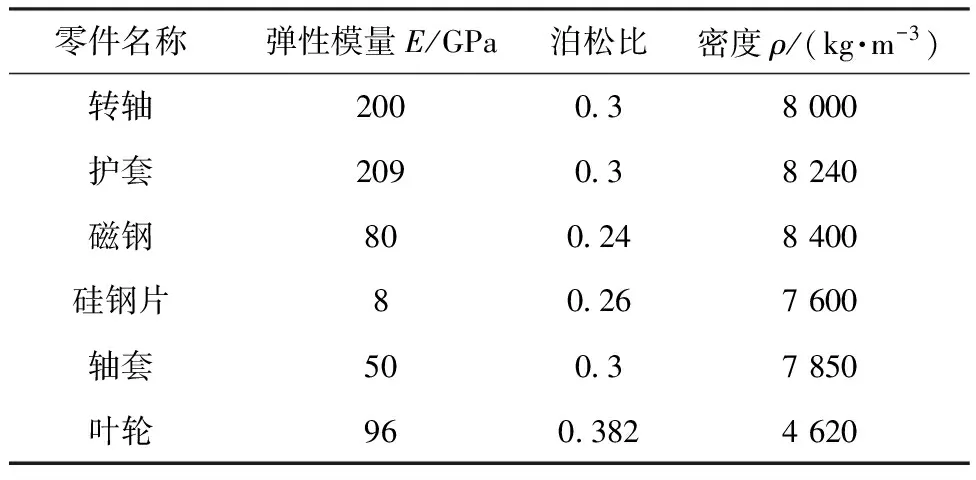
表1 转子各零部件材料参数

1.2 运动方程

转子动力学通用运动方程:

(1)

式中:M为质量矩阵;C为阻尼矩阵;K为刚度系数矩阵;F(t)为激励。

简化边界条件对转子做自由模态分析,转子为自由振动时不考虑阻尼,且没有外界激励,即阻尼矩阵C和激励F(t)均为0,则运动方程可以简化:

(2)

假设系统做简谐振动,即x=Xsin(ωt)时,则式(2)可简化:

(K-Mω2)X=0

(3)

式中:X为特征向量;ω为转子的固有角频率,通过f=ω/(2π)可以计算出转子的固有频率。

矩阵求解可以转化为特征值和特征向量的求解问题,即:

|K-Mω2|=0

(4)

系统质量刚度为固有属性,特征向量X为转子的主振型。从公式可以得出,转子的固有属性质量以及刚度决定转子的固有频率和振型。

1.3 有限元仿真分析

将建好的转子三维模型导入ANSYS软件进行自由模态仿真分析。为了验证建模的准确性,分别对单转子(转子不装配叶轮)和转子带叶轮两种状态进行自由模态分析。在实际工况中,转子工作转速一般靠近低阶固有频率,所以仅分析转子前10阶模态[7]。单转子和转子带叶轮前10阶固有频率分析结果如图2所示。结果显示,前6阶固有频率均接近0,且未出现明显变形,不是固有模态。固有频率和振型如图3所示。从振型云图可以看出,8阶、10阶为前2阶固有模态。

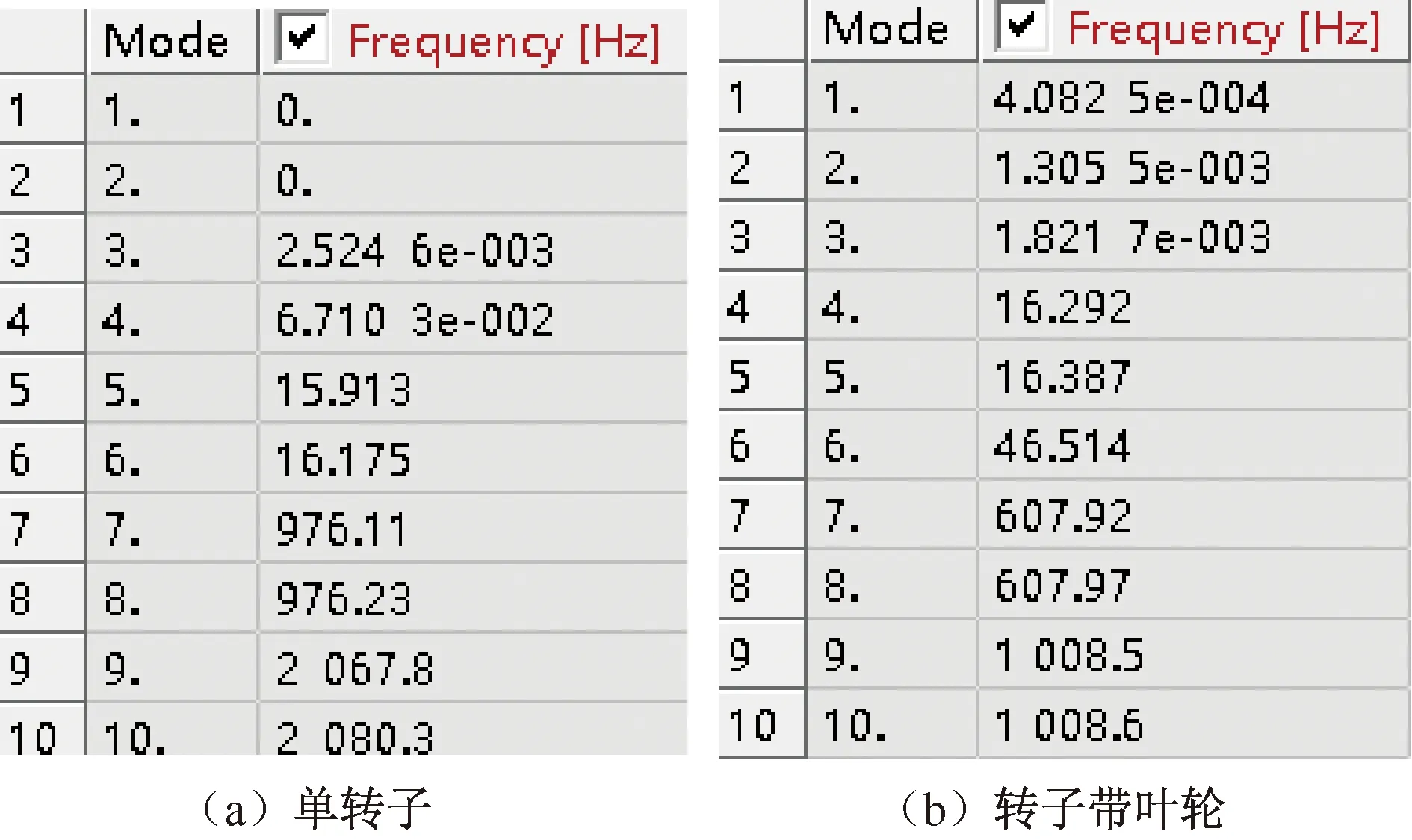
图2 固有频率计算结果

从图3可以看出,转子模态振型中存在振动几乎为0的点,这些点称作节点。并且可以看出,1阶弯曲有2处节点,如图3(a)、图3(c)所示;2阶弯曲有3处节点,如图3(b)、图3(d)所示。在后续模态实验时,力锤敲击需要避开节点,才能将对应阶次的模态激发出来。

2 模态实验

2.1 实验原理

为了验证本文转子建模方法的合理可行,需要进行实验验证。为了准确获得转子模态频率,可以对转子进行锤击法模态实验[8]。模态实验测试示意图以及现场实验如图4、图5所示。实验装置包括数据采集系统和计算机、弹性绳、转子、激励锤、加速度传感器等。为了模拟转子模态分析的自由边界条件,忽略转子的支撑影响,实验时采用弹性绳将转子悬挂起来,此时可以近似认为转子处于自由状态,测得的频率可以认为是转子固有频率。加速度传感器沿转子轴向均匀布置,力锤和加速度传感器信号接入数据采集系统。

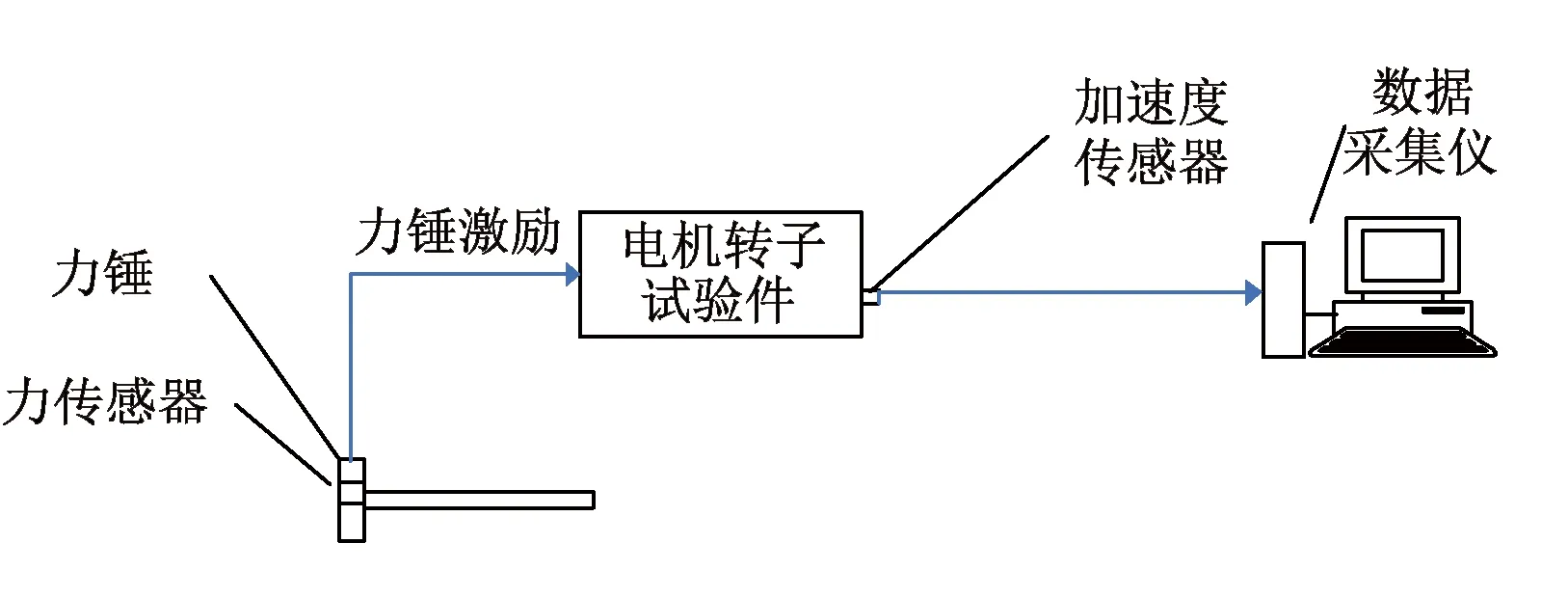
图4 模态测试及分析系统示意图

图5 转子自由模态实验

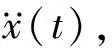
通常结构的频率响应函数:

(5)

对式(5)两边同时做拉式变换,由于初始值不会影响转子的固有特性,所以将初始值设为0,则可以得到:

{s2m+sc+k}X(s)=F(s)

(6)

式中:X(s)和F(s)对应x(t)和f(t)拉式变换,其中s=δ+jω为拉式变换因子,忽略阻尼的影响,通过拉式变换可以获得激励位置的频率响应函数:

H(ω)=1/(-ω2m+k)

(7)

通过式(5)得到转子的频率响应函数,即力锤激励输入和加速度传感器输出信号经过数据采集仪做数据处理就能测得转子的频率响应曲线,根据频率响应曲线可以识别转子各阶固有频率和振型。

模态实验用力锤对转子进行锤击时,锤击点要避开模态节点,因为锤击点与某一阶模态节点重合时无法激发出该阶模态。根据模态仿真分析得到的模态振型确定锤击点,避开模态节点。

2.2 结果分析

通过力锤单点激励测得实验数据,实验时在转子上多点位置进行激励,并且每个点取3次敲击实验平均值。单转子和转子带叶轮实测频率响应曲线如图6、图7所示。固有频率值为频率响应曲线峰值点对应的横坐标值,根据实测频率响应曲线,得到前2阶固有频率值。固有频率仿真值与实验值对比如表2所示。

表2 模态仿真值和实验值对比

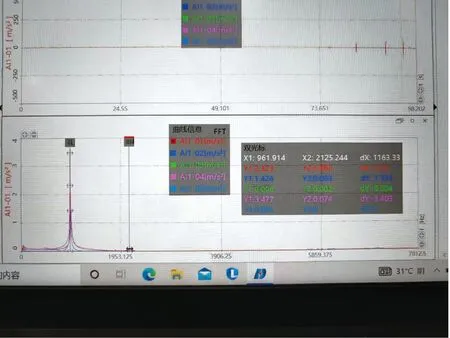
图6 单转子频响曲线

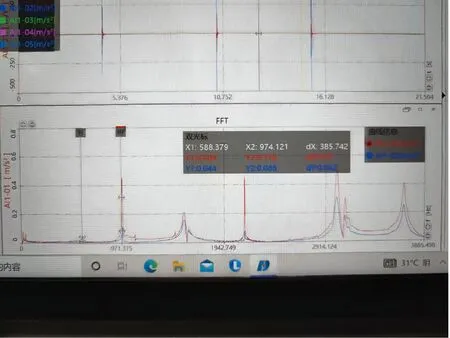
图7 转子带叶轮频响曲线

通过表2比较转子模态仿真值和实验值,本文转子模型计算的1阶和2阶固有频率与转子实际固有频率最大误差为3.54%,验证了本文建模方法的合理可行性,为后续三段式转子高速永磁电机转子动力学设计优化提供参考。

3 结 语

针对三段式转子结构,本文提出一种建模方法,并将这种方法应用于某磁悬浮高速电机转子(额定转速30 000 r/min)的仿真分析,得出如下结论:

1)转子上各零部件根据装配关系设置接触关系,各零部件材料参数按正交异性设置弹性模量,轴向弹性模量进行一定程度的削弱,通过仿真计算获得了转子前2阶弯曲固有频率和振型;

2)通过锤击法自由模态实验,得到转子前2阶固有频率与仿真计算值进行比较,两者误差率小于5%,证明了建模方法的合理可行,为后续三段式转子高速永磁电机设计以及转子动力学优化提供参考。