基于新型指数趋近律的PMSM滑模控制研究*

陈德海，曹永康，邵 恒，杨 程，邱福亮

（江西理工大学 电气工程与自动化学院，江西 赣州 341000）

0 引 言

由于永磁同步电机（permanent magnet synchronous motor，PMSM）具有结构简单、体积小、效率高、稳定可靠等优点，应用前景良好，吸引了国内外众多专家人士，其相关领域目前主要集中在数控机床、机器人、新能源汽车等。

由于PMSM系统具有非线性、多变量、强耦合等特点，而传统的PI控制虽然具有算法简单、可靠性高、易于调节等优点，但当控制系统遭受外界干扰或者电机内部参数发生改变时，PI控制抗干扰能力较弱，鲁棒性差。为此，形成了许多新的控制算法，如自适应控制、模糊控制、神经网络控制、滑模控制（sliding mode control，SMC）等。其中SMC由于抗扰性强、响应速度快、稳定性高等特点，所以经常被应用于PMSM控制系统中，由于SMC中的开关切换会导致出现抖振，使其难以发挥优越性，于是研究者们通过对传统趋近律的改进，并构建了新的滑模速度控制器，以达到削弱抖振以及提高系统响应速度的目的。文献［1］在传统指数趋近律等速项和指数项中，引入了系统状态变量的幂次项，抖振得到削弱，但力度不足。文献［2］在传统指数趋近律的等速项上引入了系统状态变量的绝对值项，并且以饱和函数sat（s）取代符号函数，曲线平滑度得到提高，补偿效果良好。文献［3］采用了一种新型的指数趋近律，简单引入了系统状态变量，并设计了滑模控制器，加快了响应速度，并且无超调，更快到达稳定状态。文献［4］引入了系统状态变量和状态变量导数的多项式，并且去除了传统的符号函数，控制效果得到提升。文献［5］引入状态变量幂次项，将等速项系数和指数项系数改成倒数关系。文献［6］提出一种带饱和函数的幂次趋近律，针对不同阶段进行速度的自适应调节，系统动态品质得到一定改善。文献［7，8］用饱和函数代替了符号函数，新加入一个函数，抖振和超调得到控制，但计算较复杂。文献［9～13］改变了传统的等速项，对符号函数做了优化或替换，使之具备趋近速度的自适应调节能力，但较复杂，参数较多。文献［14］在传统指数趋近律之中，结合了终端吸引因子以及状态变量的幂函数，控制效果显著。

本文设计了一种新型指数趋近律，将趋近速度与滑模面函数的绝对值结合起来，在等速项中引入包含对数项的分数多项式，并对符号函数进行平滑处理。

1 PMSM数学模型

设PMSM满足以下条件：1）三相定子绕组相互对称且相同；2）转子永磁体在气隙磁场中以正弦波分布；3）忽略定子铁心饱和，磁路为线性，电感参数不变；4）转子上没有阻尼绕组。

选用id＝0的转子磁定向控制方法，在此选择转子坐标系下的数学模型，PMSM定子电压方程为

式中 ud，uq为d轴、q轴定子电压分量；id，iq为d轴、q轴定子电流分量；R为定子电阻；φd，φq为d轴、q轴永磁体磁链分量；φf为永磁体磁链；ωe为电角速度。

电磁转矩方程为

式中 Te为电磁转矩，Pn为电机极对数。

机械运动方程为

式中 J 为转动惯量，TL为负载转矩，ωm为机械角速度，ωe＝Pnωm。

2 新型指数趋近律设计

2.1 传统指数趋近律

指数趋近律算法［15］如下

式中 ε为趋近系数，q为指数趋近系数，ε ＞0，q ＞0。s为滑模面函数，sign（s）为不连续的符号函数，-εsign（s）为等速趋近项，-qs为指数趋近项。当系统状态点离滑模面较远时，处于趋近运动过程，此时由等速趋近项和指数趋近项共同作用，其中指数趋近项起主要决定作用，q 值越大，到达滑模面越快，ε 值越小，到达滑模面时的速度越小，抖振越小；当系统状态点到达滑模动态时，处于滑模运动过程，此时指数趋近项趋近为零，主要由等速趋近项起决定作用。合理准确地调节ε与q的大小，才能达到加快系统响应速度的效果，同时还能削弱抖振，提高系统的动态品质。

2.2 新型指数趋近律

设计了一种新的指数趋近律，表达式如下

其中，ε ＞0，q ＞0，a ＞0，b ＞1。

在传统指数趋近律的等速项中加入一个f（s）函数，将运动点的趋近速度与离滑模面的远近结合起来，使得系统能够自适应地调整趋近速度。改进的指数趋近律相比传统指数趋近律，当运动点离滑模面较远时，处于趋近运动阶段，此时｜s｜较大，f（s）趋于无穷，εf（s）大于ε，在远处的趋近速度得到提升，趋近时间加快，提高了系统响应速度。当离滑模面较近时，处于滑模运动阶段，此时｜s ｜较小，趋近于0，f（s）则趋近于a／（1 ＋a），小于1，则降低了在滑模面附近的趋近速度，削弱了抖振，控制精度得到提高。

由于符号函数sign（s）不是连续的，是造成抖振的一个重要因素，所以对它进行平滑处理，如下所示

式中 σ为数值较小的正数。

2.3 新型指数趋近律性能分析

为了验证新型指数趋近律的有效性，采用经典的控制系统［16］对趋近律方法进行对比。被控对象如下

滑模面函数

其中，c ＞0，跟踪误差

其中，θd为期望位置，θ为实际位置。经过计算得到

式中 slaw为趋近律。整理可得控制输出

式中 c ＝15，期望位置信号θd（t）＝sin t。将传统指数趋近律和新型指数趋近律代入控制输出表达式内，其中传统指数趋近律与新型指数趋近律系数q ＝30，ε ＝15，a ＝50，b ＝10，σ ＝1。经过仿真，两种趋近律作用效果对比如图1所示。

图1 两种指数趋近律性能对比

从图1中可得出，相比传统指数趋近律，新型指数趋近律在趋近速度方面有所提高，趋近过程时间缩短，以及抖振的抑制得到提升。新型指数趋近律总体性能高于传统指数趋近律。

3 滑模速度控制器设计

3.1 控制器设计

在id＝0转子磁场定向控制策略下，并满足Ld＝Lq＝Ls，定义PMSM系统状态变量

式中 ωref为电机的给定转速，是一个常数，ωm为实际转速（机械角速度），Ls为定子电感。

令D ＝1.5Pnφf／J，u ＝iq，由上式得到空间状态表达式

对滑模面函数进行定义

式中 c 为待定系数，c ＞0，x1为速度差，x2为速度差的导数。然后对上式进行求导，可得

求得控制器表达式

继而可得q轴参考电流

由控制器表达式和q轴参考电流可知，两者都含有积分项，所以在削弱抖振的同时，稳态误差也得到了降低，系统动、静态品质得到提高。

3.2 控制器稳定性分析

定义李雅普诺夫（Lyapunov）函数

对其求导，则有

由于ε ＞0，q ＞0，s·sign（s）＞0，f（s）也大于0，所以V˙＜0，满足可达性条件。

4 仿真与实验分析

建立系统仿真模型，旨在验证新型指数趋近律的可行性，本文采用PMSM双闭环调速系统控制，其中电流环采取传统的PI控制方法，速度环从早前的PI 控制替换为SMC法，并基于新型指数趋近律构建改进型滑模速度控制器。系统框图如图2 所示，并且与PI 控制、传统指数趋近律SMC作仿真对比。电机参数与仿真条件如表1所示。

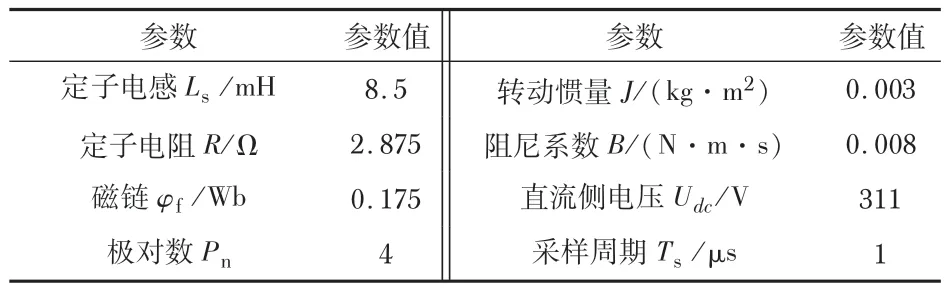
表1 电机参数

图2 PMSM调速系统

滑模速度控制器参数设置：c ＝100，q ＝250，ε ＝50，a ＝1，b ＝6，σ ＝0.008。PI电流环参数设置：比例系数kp＝10，积分系数ki＝400。仿真时间0.5 s，初始给定转速N*＝600 r／min，零时刻负载转矩T1＝0 N·m，在t ＝0.2 s 时，外加负载TL＝10 N·m。

从图3 中可以看出，在系统启动过程中，PI 控制超调最大，约在0.13 s处稳定；传统指数趋近律SMC超调较小，约在0.1 s处稳定；新型指数趋近律SMC接近无超调，约在0.09 s处稳定。由图4 可得，三者之中，新型指数趋近律SMC抖振幅度最小，约为89 r／min，波动率14.83%，并最先稳定下来，趋近过程时间短，波动范围最小；传统指数趋近律SMC抖振幅度次之，为99 r／min，波动率16.5%，趋于稳定时间居中；PI 控制抖振幅度最大，为123 r／min，波动率20.5%，趋于稳定的过程较长。

图3 转速曲线

图4 突加负载的转速曲线

由图5结果表明，在PMSM调速系统的启动过程中，采用新型指数趋近律SMC和传统指数趋近律SMC能够使电磁转矩更加快速稳定地到达稳态，并且无超调，PI 控制的电磁转矩曲线回归稳态时存在明显的超调。在0.2 s突加负载后，PI控制稳定过程最长，约0.08 s；传统指数趋近律SMC稳定时间次之，约0.06 s；新型指数趋近律SMC最快，约0.05 s，其稳定后波动范围也最小。

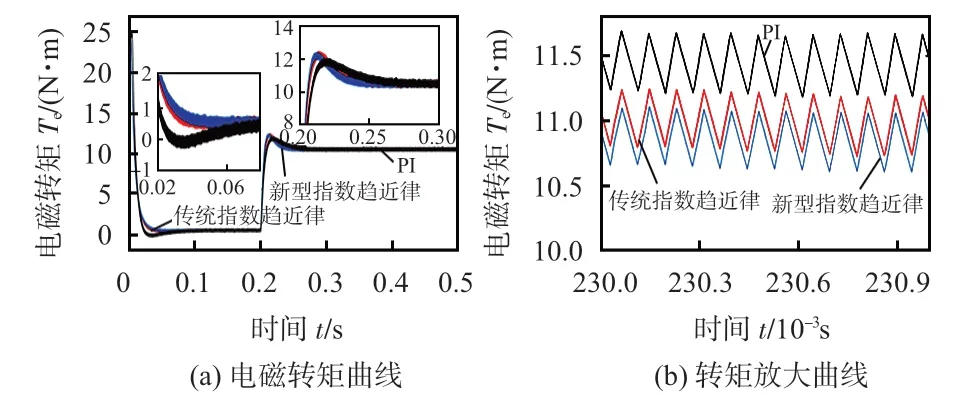
图5 电磁转矩曲线性能对比

从图6中可以得出，PMSM调速系统刚启动时，PI控制振幅较大，并且电流曲线紊乱，分布不均匀；而传统指数趋近律SMC和新型指数趋近律SMC 振幅较小，曲线稳定平缓有序。在0.2 s突加负载后，新型指数趋近律SMC 电流波动幅度最小，只有1.2 A，三相电流曲线最为平整，并且更快稳定下来；传统指数趋近律与PI 控制效果稍显差异，前者电流波动约1.9 A，后者约1.8 A。

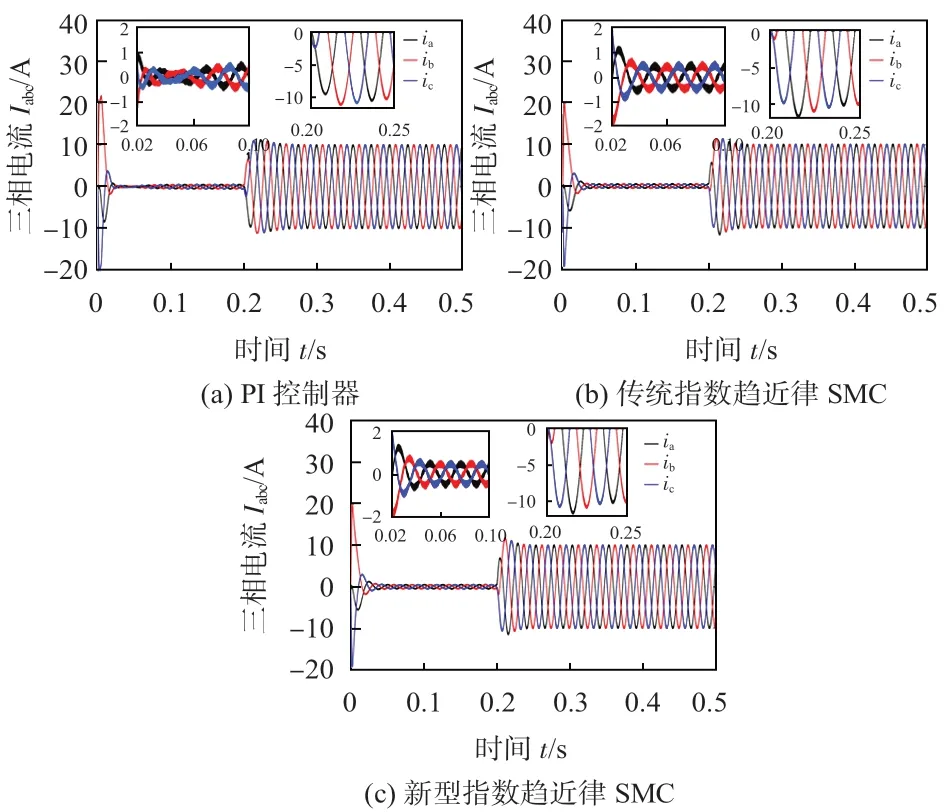
图6 PI控制器和传统／新型指数趋近律SMC下的电流波形

综合仿真图和分析解释，可知改进后的指数趋近律相比于传统指数趋近律和PI控制，超调更小，抖振更小，能够快速稳定地达到稳态，控制精度更好，鲁棒性更强。

5 结束语

本文基于传统指数趋近律，在等速项中引入一个涵盖对数项的分数多项式，将趋近速度和滑模面函数的绝对值结合，实现趋近速度的自适应调整；而后对符号函数进行平滑处理。并且进行模型的搭建以及仿真，构造对应的滑模控制器与传统指数趋近律、PI控制方法进行对比实验。实验结果表明：采用新型指数趋近律能够很好地降低系统超调量，快速稳定地达到稳态，鲁棒性有了显著提高，控制效果得到改善。