基于四叉树的ORB-LBP改进算法*
2023-10-25陈易文储开斌冯成涛
陈易文,储开斌,张 继,冯成涛
(1.常州大学 微电子与控制工程学院,江苏 常州 213164;2.常州大学 阿里云大数据学院,江苏 常州 213164)
0 引 言
图像的特征提取和匹配是同时定位与地图构建(simultaneous localization and mapping,SLAM)[1,2]的基础问题,影响着整个SLAM系统的效率与精度。Lowe D G在1999年首次提出尺度不变特征变换(scale-invariant feature transform,SIFT)算法[3],并在2004 年进一步改进该算法。Bay H等人在2008 年借鉴SIFT 算法提出了加速鲁棒特征(speeded up robust feature,SURF)算法[4],在一定程度上解决了SIFT 算法计算复杂度高、计算时间长等缺点;Rublee E 等人提出了定向二进制简单描述符(oriented FAST and rotated BRIEF),ORB)描述算法[5],该方法图像匹配速度快,但其匹配效果较差。
近年来,出现了很多ORB算法的改进方法。姚晋晋等人[6]提出了一种基于改进四叉树ORB 特征均匀算法,有效提高了特征提取的均匀度和效率;孙浩等人[7]通过区域划分的方式,使提取到的特征点分布更为均匀,同时速度也有较大的提升;汪永生等人[8]通过改进的ORB 特征描述子方法对待匹配的特征点进行描述,有效提高了图像匹配质量;董永峰等人[9]在SURF 算法基础上融合二值稳健独立基本特征(binary robust independent element feature,BRIEF)描述子,在提升匹配效率和准确度的同时,可以满足实时性的要求;Li S等人[10]提出一种融合BRIEF和FREAK描述子的改进ORB算法,在尺度变化、明暗度变化时,特征匹配率和鲁棒性都有了很大的提升。
上述改进在一定程度上提升了ORB匹配精度,但ORB特征点在图像平面仍然分布不均匀,在图像变化不明显的区域,不能检测到特征点,而在一些图像变化剧烈的地方容易出现特征点聚集现象,对后续特征匹配与位姿估计的精度会有巨大的影响。
本文针对特征点分布不均匀、匹配精度差的问题,对ORB算法进行了改进,通过建立四叉树及融合BRIEF—局部二值模式(local binary pattern,LBP)的方法,以期达到在少量增加计算时间的前提下,特征点分布更为均匀、匹配精度更高。
1 传统ORB算法
ORB是一种局部特征提取方法,它利用加速分割测试特征(features from accelerated segment test,FAST)[11]关键点检测器提取图像特征关键点,利用BRIEF[12]描述子提取图像特征描述子。
1.1 FAST角点检测算法
以待检测像素为圆心,3 个像素值为半径,做一个圆,与圆相交的共有16 个像素,检测16 个像素中与中心点的像素差大于某个阈值T 时,计数n 加1,若16 个点检测完成时n >N(N 一般取11 或者9),则认为该待检测像素为角点,然后循环此过程检测每一个像素[11]。
1.2 BRIEF描述子
以检测到的角点附近框选一个方形窗口,在这个窗口内随机挑选出n组点对,再对每一个点比较亮度值,对所有n组点对都进行比较后生成了一个长度为n的二进制字符串,即BRIEF描述子[12]。
图1为传统ORB的特征点检测结果,可以看出所检测到的特征点都容易集中于部分区域,特征点分布极度不均匀;只有在一部分特征明显的区域存在密集的特征点,而在大部分区域都未能检测到特征点,因此会导致后续匹配精度差。

图1 传统ORB特征点检测
图2为传统ORB特征点结合暴力匹配得到的匹配结果,可以看出:所匹配的精度不高,匹配效果差,多处出现了误匹配现象。

图2 传统ORB特征点匹配
2 基于融合描述子的改进ORB算法
图3为算法整体流程。首先,构建图像金字塔,通过划分网格计算角点提取阈值来提取FAST角点;其次,通过构建四叉树使角点分布均匀;然后,通过融合BRIEF-LBP的方法对提取的角点进行特征描述;最后,利用随机抽样一致性(random sampling consistency,RANSAC)的方法进行特征匹配。

图3 本文算法流程
2.1 构建图像金字塔
本文通过建立图像金字塔,以最底层金字塔为原始图像,每向上1层,进行一定比例的缩放,得到不同分辨率的图像,匹配不同金字塔层上的特征点,实现了尺度不变性。
图4为不同金字塔层所检测的特征点结果,分别建立了7层、5层、3层金字塔,可以看出在不同层数金字塔下图像所提取到的角点都有所区别。通过实验,最终建立3层金字塔层,达到效果最优。

图4 不同金字塔层特征点
2.2 角点提取
将图层划分为M×N的网格,记录每个网格中任意一个像素点的灰度值为Ip,网格平均值灰度值为Iq,并定义阈值T
式中 α为一个自适应变量,本文α取1.2;m为网格内像素点数量。在每个网格中对各像素与阈值T 进行比较,进行角点提取,若在该网格中未提取到角点,则将阈值T降低为原有的1/2,再进行角点提取。遍历所有网格,直至提取到的角点数量满足设定的角点数量。
图5为自适应阈值下的角点提取,可以看出角点的分布情况较图4(c)3 层金字塔提取到的特征点分布相比已经有了改善,但提取到的角点在一定程度上仍会在部分网格内密集分布。由于这部分角点对阈值的响应较大,角点占据极大一部分所要求的角点数量,导致一些网格内还未检测到角点就结束角点提取操作。

图5 角点提取
2.3 构建四叉树
首先,通过2.2节的方法对整张图像进行角点检测;然后,将整个图像空间划分为4个相同的子空间,若在子空间内检测到的角点数量大于1,则继续将该子空间分裂为4个新的子空间继续检测;但若特征点数量太多,会导致四叉树的深度过深,在进行空间检索时效率会比较低下。因此,本文限制了四叉树的深度为4 层,若深度达到4 层后子空间内的角点数量仍大于1,则留取子空间内响应值最大的角点,舍弃其他角点,如图6所示。

图6 四叉树示意
2.4 BRIEF-LBP融合描述子
ORB使用改进的BRIEF进行特征描述,减少了特征匹配所需的时间,但是其描述符的相关性仍然很大,使得图像信息的利用不完整,容易导致特征点的不匹配。针对上述问题本文将BRIEF描述子与LBP描述子融合的方法,其融合流程如图7所示。

图7 BRIEF-LBP描述子融合流程
首先,通过FAST 角点检测算法进行特征点的提取。以特征点为中心,选取S ×S的邻域窗口,在窗口内随机选取2 ×2的像素点块,比较两者像素点块像素平均值大小,进行二进制赋值,如式(2)所示
式中 I(r1,c1)和I(r2,c2)分别为(r1,c1)和(r2,c2)处像素的强度。如果I(r1,c1)小于I(r2,c2),则λ =1;否则,λ =0。重复操作,最终形成一个256位的二进制编码。
其次,以特征点为中心,半径为R 做圆形区域。一个中心像素点(x,y)周围的其他像素点gk的坐标(xk,yk)可以表示为
式中 R为圆形LBP 半径,r 为第r 个采样点,k 为样本点数量。对计算得到的坐标采用双线性内插值取整,以取整后的坐标作为选取像素点的坐标,比较中心像素点与选取像素点的灰度值,若中心点的灰度值大,则记为0,否则为1。重复操作,直至得到128 位二进制值,并将此二进制值循环排列直至得到最小的一组二进制值便作为该像素点的LBP值。
本文将得到的256 位BRIEF 描述子与128 位LBP 描述子级联得到新的384 位的二进制描述符,将该新的描述子作为特征点的描述子。
2.5 特征匹配
本文采用暴力匹配方法对特征点的进行匹配,对所有待匹配的特征点进行汉明距离测试,舍弃汉明距离较大的特征点,对于剩下的匹配点利用RANSAC[13]方法进行进一步的剔除。
3 实验验证
所用的实验平台配置为Intel®CoreTMi5—8265U,内存1.60 GHz。采用了EuRoC公开数据集[14]中的图片,该数据集包括了视觉(双相机)测量得到的数据。将本文算法与ORB算法、SIFT算法以及文献[9,10]中改进的ORB 算法进行对比实验验证,分别做了特征点分布均匀度实验,算法耗时实验和算法匹配召回率实验。本文采用了基于区域统计信息计算分布均匀度的方法[15],如图8 所示。通过将图像划分为上、下、左、右、左上、右下、左下、右上、中心和外围10个区域。统计每个区域所检测到的特征点数量,然后统计每个区域分布向量的方差V。计算所得特征点的分布均匀度u如下

图8 图像分割示意
式(4)为朱海峰等人[15]给出的特征点分布均匀性的客观评价标准,利用式(4)可以计算得到整幅图像内特征点的分布均匀度,该数值越小,就表示不同区域内的特征点数量差别越小,分布均匀度越好。
对实验结果进行均匀化可视化计算,本文选取了Eu-Roc数据集中的部分图像进行特征点均匀化实验以及耗时实验,实验结果分布记录于表1 和表2。由表1 分析可知,对比传统的ORB算法和文献[9,10]改进算法,本文算法对特征的均匀度有较大的提高。
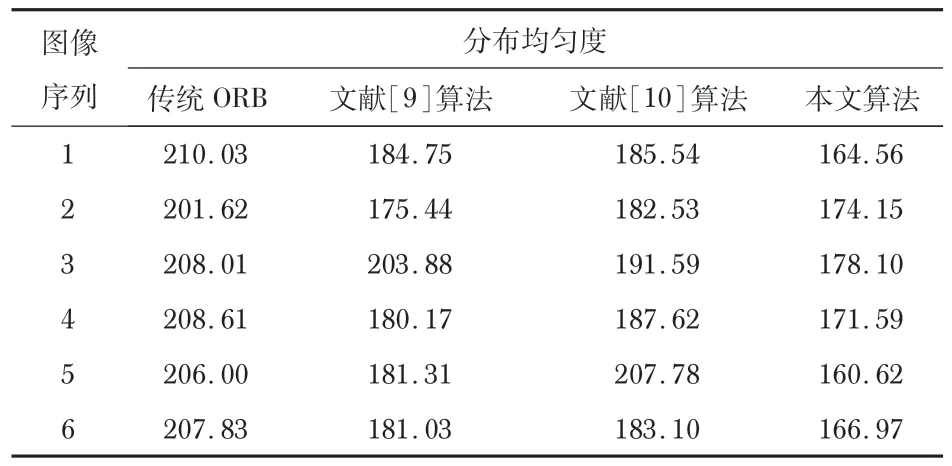
表1 不同算法分布均匀度比较

表2 不同算法时间比较
表2为不同算法所耗时间比较,可以看出:本文算法比ORB算法所耗时间稍增加了一些,但比文献[9,10]所改进算法仍稍快一筹。
图9为传统ORB算法、SURF 算法和本文算法特征点提取结果,从图中可以看出传统ORB算法的提取结果极为不均匀,大部分都集中于一部分地区,无法有效得到整幅图像的信息;SURF算法提取结果比与ORB算法相差不大;而本文算法提取到的特征点遍布整幅图像。

图9 特征点提取结果
选取EuRoc数据集,并将数据集中的图像做明暗度变化、缩放、旋转操作,通过本文算法提取400 个特征点进行匹配实验,实验结果如图10所示。图10(a)为原始图像匹配结果,图10(b)为改变图像明暗度后匹配结果,图10(c)为图像缩小50%后的匹配结果,图10(d)为旋转90°后的匹配结果。匹配实验结果可以看出,本文算法对于特征匹配结果质量高,匹配结果都未出现误匹配。结果表明:本文算法对于图像明暗度变化、图像缩放、旋转等操作都具有较强的鲁棒性。

图10 本文算法匹配结果
本文通过大量实验比较了5 种算法的平均所用时长,结果如表3。结果表明,SURF 算法所用时间最长,ORB 算法所用时间最短,本文算法略高于ORB 算法,仍远低于SURF算法,对比文献[9,10]改进ORB 算法,本文算法速度更快。

表3 不同算法平均所用时间 s
召回率可以反映匹配算法的查全率,即正确匹配占实际全部匹配的比例。本文经过了多次实验,得到的结果如表4。对比ORB算法,本文算法的召回率有明显的提升;比SURF算法仍有不足之处,因为SURF 是构造尺度空间,通过高斯微分函数识别兴趣点,而不是直接提取角点,鲁棒性好。文献[10]改进ORB算法对于正常的图像,具有较高的召回率,但其对于旋转的鲁棒性较差。而本文算法在改变明暗度、对图像进行缩放、旋转操作时,召回率变化不大,可以看出,本文算法对图像明暗变化,缩放旋转等操作时都有较强的鲁棒性。

表4 不同算法平均召回率 %
4 结束语
本文算法通过构建四叉树和融合BRIEF-LBP 描述子的方法来实现ORB算法中特征点的均匀分布以及特征匹配的准确性。首先,对输入图像构建金字塔尺度空间,在每一图层上进行FAST关键点的检测;其次,通过构建四叉树来限制特征点分布;最后,在生成描述子的过程中用128 位LBP描述算子融合BRIEF中256位描述子形成新的384位的特征描述子,新的描述子可以更充分的表达图像信息,使得匹配结果更为精确。实验结果表明:对比传统ORB,本文算法虽然在速度上比ORB算法降低了5%,但均匀度提升了66左右,召回率也提升了10%;与其他改进算法[9,10]相比,本文算法速度提升了2%~5%的同时,特征点分布均匀度提升了48 和49,召回率也提升了36.63%和4.925%。实现了在少量增加计算量的同时,特征点均匀度和匹配精度方面效果有较大提升。
