极坐标像素平铺法获取整体式立铣刀螺旋槽端截面廓形的研究＊

游明琳

（贵州师范大学机械与电气工程学院，贵州 贵阳 550001）

整体式立铣刀因具备良好的切削加工性能而在制造业中得到广泛应用[1]。螺旋槽是整体式立铣刀的重要组成部分，其几何结构直接影响铣刀的切削性能和加工零件的表面质量，因此需要通过建模仿真的方式进行预先分析，并计算前角、芯径和槽宽等关键几何参数[2-3]。分析和计算方式可以先精确获取螺旋槽截面廓形再求相关参数，或者先对螺旋槽准确建模再测算相关参数[4]。近年来众多学者致力于研究螺旋槽建模及重要参数求解，主要提出了3 种方法：解析法、布尔运算法和图形法[5]。（1）解析法以啮合原理为核心，根据砂轮与刀具的包络运动关系，求出砂轮与螺旋槽之间的瞬时接触线方程。Kang S K 等[6-7]建立了刃磨过程中砂轮与铣刀之间的接触线方程，并给出了螺旋槽的计算方法。Dogrusadik A[8]将包络运动关系应用在球头铣刀螺旋铣削中，给出了螺旋槽横截面轮廓的方程。Rababah M[9]详细介绍了解析法在刀具加工和建模中的应用。Habibi M 等[10]提出了利用虚拟磨削曲线特征求解螺旋槽几何轮廓的方法。Chen Z 等[11]

基于砂轮与刀具的包络运动关系，用迭代法计算铣刀螺旋槽二开槽磨削的算法。Shen C 等[12]实现了砂轮加工刀具螺旋槽的参数化设计。

（2）布尔运算法借助于三维建模软件的布尔（Boolean）运算功能，按照加工轨迹细分，不断调整砂轮与被磨刀具之间姿态，连续进行布尔运算操作，从而获得螺旋槽三维模型。Kim J H 等[13]利用三维软件建立了立铣刀螺旋槽的实体模型，并定义了前刀面前角、芯径等刀具几何参数。Pei Q 等[14]利用三维软件建立了球头铣刀数控磨削建模与仿真的实用方法。Li G C 等[15]通过布尔运算方法模拟实际螺旋槽的磨削过程，提出了由已知的砂轮几何外形得到螺旋槽模型的方法。Tost D 等[16]对刀具的横截面进行动态布尔运算并重建了螺旋槽三维模型。

（3）图形法，主要是将砂轮进行离散化表达，然后根据砂轮与被磨刀具之间的相对空间位姿几何关系，将螺旋槽描述为若干切削轨迹叠加包络形成[17]。图形法所采用的几何理论简单，几乎适用于任何类型砂轮形状的加工计算，但每个离散点都由迭代运算产生，所以识别或提取螺旋槽截面离散点的边界成为图形法研究的难点。众多学者纷纷在图形法的廓形识别和提取方法上不断进行创新，研究出各种各样图形图像法，使得算法能够更高效、更高精度识别或提取理论截面廓形边界。

Li G C 等[18]将螺旋槽刃磨过程转化为离散点云处理，并将立铣刀端截面离散为一系列圆环，通过这些离散圆环内边界点的计算获得螺旋槽端面轮廓。中国台湾的吴育仁等[19]提出RRS （radial-ray shooting）用以取代传统的齿轮包络原理进行圆柱形成形磨齿及模拟加工的计算求解出精确的工件齿形。沈志煌等[20]提出DSG（digital scanning graphic），通过扫描屏幕上刀具切削轨迹包络面的像素点，从而获得转子的轮廓数据。

本研究探索了一种图形图像法求解螺旋槽廓形的新算法，能获取满足设计和加工要求精度的刀具螺旋槽端截面廓形，简称极坐标像素平铺法（polar pixel method，PPM）。该方法直接由离散点云结合数学形态快速求解螺旋槽横截面轮廓点云图像提取边界，运算过程直观，解值稳定，避开求解接触线方程，是图形法又一创新研究和应用。

1 砂轮磨削螺旋槽包络原理

砂轮磨制螺旋槽的实际运动过程是砂轮以确定的位姿沿棒料轴线运动，同时棒料绕轴线旋转运动，二者共同构成螺旋运动。在对螺旋槽磨制过程进行分析时通常将棒料看作固定不动，砂轮在棒料坐标系下做螺旋运动，这样就将两个物体的运动关系转换为只有砂轮的运动。建立刀具坐标系[o;x,y,z]和砂轮坐标系[o′;X,Y,Z]，如图1 所示。其中砂轮轴线和刀具轴线间的夹角为Σ（安装角），两坐标系原点沿y轴方向的距离为a（中心距），沿x轴方向的距离为e（ 偏心距），沿z轴方向的距离为d（安全距离）。

设砂轮轴截面轮廓方程f(t)，在砂轮坐标系[o′;X,Y,Z]中建立砂轮回转面方程（1）。

式中：t为参变量，t∈[0,b]；b为砂轮厚度； φG为参变量，φG∈[-π,π]，表示在砂轮某一厚度t对应的平面内绕砂轮轴线旋转过的角度。

如图1 所示，根据砂轮安装位置关系和坐标变换原理，容易得出刀具坐标系 [o;x,y,z]与砂轮坐标系[o′;X,Y,Z]的变换关系变换矩阵M为

根据变换关系可得到砂轮回转面点云转换到刀具坐标系[o;x,y,z]下的方程为

则可求得在刃磨过程中砂轮轮廓面点云形成的曲线簇方程为

用垂直于刀具轴线的平面z=0 截取螺旋槽点云形成的曲线簇，获得曲线簇在该平面上留下的点云，令z=0，由式（5）可得θ=-zg/p，进而可求得砂轮做螺旋运动包络形成的运动轨迹点的端截面投影为

设刀具半径为r，则螺旋槽端截面包络点满足在限制条件x2-y2≤r2内。

2 螺旋槽轮廓提取方法

PPM 法是借用计算机图像处理的原理，将大量点云数据转成极坐标像素后结合数学形态学快速获得点云边界的一种方法。首先将砂轮离散化处理，并根据砂轮与刀具之间的相对位姿关系（即加工安装参数）进行砂轮与刀具的坐标变换，提取刀具外圆内所包络数据点云，即刀具螺旋槽端截面点云。然后将螺旋槽端截面点云由笛卡尔坐标转换为极坐标，生成二值图像并结合数学形态学提取图像边界，最后将图像边界还原获得螺旋槽廓形边界。

2.1 包络运动的点云生成

根据图1 设定砂轮与刀具的空间位置关系，将离散的砂轮面点云在刀具坐标系下绕z轴做螺旋运动，收集在平面（z=0）留下的所有包络点，如图2所示。

图2 螺旋槽端截面的包络点云图

设定边界条件为刀具半径r，按式（6）收集端截面在刀具外圆范围内所有包络点云，称为目标点云，即满足要求的刀具端截形点云，如图3 所示。

图3 符合刀具半径内的包络点云图

2.2 极坐标像素的数据转换

本文所研究的立铣刀螺旋槽的端面截形为圆形分布的图像，为了便于存储和计算，提出一种适合数学形态学的极坐标像素平铺方案。PPM 法采用扇区像素而不是直角像素进行平铺排列，沿圆径向均匀分为U层圆环（U为正整数），每层圆环按等弧长单位均匀划分多个扇区，设V是最内层区段中包含的扇区数（V为正整数），则第k层圆环从原点极轴开始按弧长均匀地划分为kV个扇区，其中最外圆环被分为VU个扇区部分，整个圆面就被分成个扇区部分[21]，PPM 法像素平铺方案如图4 所示。

图4 极坐标像素平铺方案

V和U的值应该正确设置，设置过小，计算效率高，但可能不能充分表示图像信息，易失真；设置较大，有利于图像的表示，但会增加计算复杂度。所以V和U的值在设定时要尽量满足所划分的极坐标像素面积大小合理，使坐标系统转换引起的图像失真处在较低水平，从而保持必要的图像分辨率。在实践中，根据扇区像素面积与直角像素面积近似和扇区像素弧长与直角像素边长近似，设置V=4。由此，螺旋槽点云在极坐标像素平铺方式如图5 所示。

图5 极坐标像素平铺法表示的螺旋槽

在整个圆面上按照等弧长方式进行平铺极坐标像素，则每个像素点是可以通过对应各自的极坐标进行转换，设极坐标系为O-ρOθ，则有任意螺旋槽点云的笛卡尔坐标(xj,yj)可转换为极坐标(ρj,θj) 。极坐标和极坐标像素之间存在相应的转换关系，如图6 所示。

图6 极坐标与极坐标像素转换

设定U和V值后，每层圆环的宽度为

在每层圆弧上按等弧长平铺扇形像素，则有每个像素的外圆弧长为

设m为圆环从原点极轴开始均分的层数序列，n(m)为第m层的扇形像素的个数，则有n(m)=mV。

此时可以将螺旋槽点云的极坐标(ρj,θj) 转成m-n坐标图。

先按式（9）计算点云所在圆环层数mj。

式中：int为取整符号。

然后按式（10）计算点云所在的扇区位置。

代入δρ=r/U和δs=2πr/UV得到

由此完成笛卡尔坐标下螺旋槽点云转换为极坐标像素的图像点阵形式，如图7 所示。

图7 螺旋槽m-n图像点阵

2.3 数学形态学提取图像边界

螺旋槽极坐标像素的图像点阵要进行数学形态学运算，需进行数据点转化为二值图像矩阵。处理方法为遍历(mj,nj)点的位置坐标置元素值为“1”，即前景像素（pixel value= 1）其余矩阵位置设置为“0”，即背景像素（pixel value= 0）[22]，建立螺旋槽点云的二值矩阵，则点云坐标完成二值化处理，所生成的螺旋槽点云极坐标像素平铺的二值图像如图8 所示。

图8 点云转换的二值图像

设A为原始二值图像，B为“结构元素”，通过膨胀运算操作见式（12），可将图像填充为连通的二值图像，如图9 所示，D(A)为膨胀后图像像素集合[23-24]。

图9 膨胀操作后图像图

式中： ⊕为膨胀运算符。

然后使用膨胀运算相同的结构元素B 进行腐蚀运算操作，见式（13），E(A)为腐蚀后图像像素集合，则可得到与元素图像等大小且连通的二值图像[23-24]。

式中： ⊕为腐蚀运算符。

再选用相同的结构原始B，进行边界β(A)的运算操作，见式（14），便可获取二值图像的边界[23-24]，如图10 所示。

图10 腐蚀操作后提取边界图

2.4 螺旋槽边界轮廓还原

由于数学形态学运算操作后的图像边界是极坐标像素二值图像廓形，将极坐标像素边界轮廓还原为笛卡尔坐标的点阵形式时，需要先将轮廓像素点坐标变换还原操作，获得螺旋槽边界点在极坐标像素坐标下点阵形式，如图11 所示。

图11 极坐标像素边界图

最后将极坐标像素边界转换为笛卡尔坐标形式，设任一极坐标像素边界点的坐标为pj(mj,nj)，则变化为对应笛卡尔刀具工件坐标(xj,yj)的表达式为

代入δρ=r/U和δs=2πr/UV得到：

转换后即可得到还原为实际比例尺寸的螺旋槽廓形点。

3 实例分析

有一实际需磨削加工的硬质合金平底立铣刀CYXV21204，其刀具参数、砂轮参数、安装参数见表1～表3。

表1 刀具参数表

表2 砂轮参数表

表3 安装参数表

在该参数条件下，离散砂轮参数φG=10 000和t=1 000，收集的螺旋槽初始目标点云数为256 365，PPM 法选择极坐标像素平铺参数U=1 000 和V=4，计算的廓形图如图12 所示。

图12 PPM 法 U=1 000 时计算的廓形图

在同等参数条件下使用解析法计算螺旋槽截面廓形，计算采样数据点为425 个，廓形图如图13 所示。

图13 解析法计算的廓形图

显然，PPM 法所求截面廓形的精度与平铺参数U和V直接相关，本实例取V=4，并分别选择PPM法在U=100、U=500 和U=1 000 时的求解情况与接触线法进行廓形比较。比较方法是沿接触线法廓形点的法线方向与PPM 法还原后廓形的交点距离作为误差的值。

（1）PPM 法U=100 时，所提取的截面廓形两者比较的误差分布情况如图14 所示，其中最大误差小于10.032 4 μm。

图14 PPM 法 U=100 与解析法廓形的误差图

（2）PPM 法U=500 时，所提取的截面廓形两者比较的误差分布情况如图15 所示，其中最大误差小于3.354 1μm。

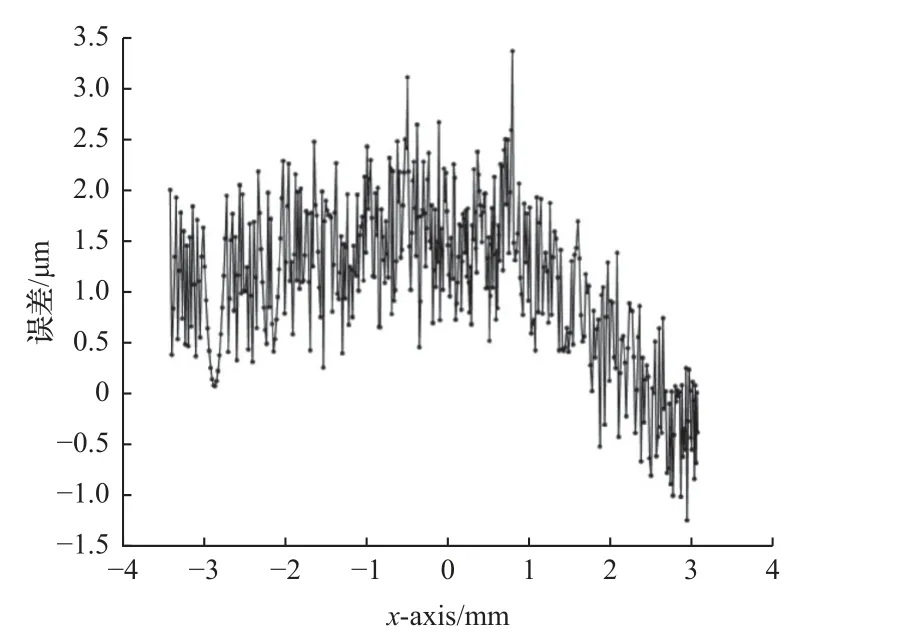
图15 PPM 法 U=500 与解析法廓形的误差图

（3）PPM 法U=1 000 时，所提取的截面廓形两者比较的误差分布情况如图16 所示，其中最大误差小于1.349 6 μm。

图16 PPM 法 U=1 000 与解析法廓形的误差图

通过PPM 法在U=100、U=500 和U=1 000 的3种情况与解析法计算结果比较分析，发现廓形误差结果随着平铺参数U增加而减小。当U=1 000 时，其计算的廓形相对解析法的廓形，误差基本在(-2 μm, 2 μm)范围内，说明PPM 法U=1 000 时足够满足设计或加工的精度要求。

4 结语

为了准确又稳定地获得螺旋槽端截面廓形，本文提出了一种新型数字化图形解法——PPM 法。该方法通过砂轮面离散成点后绕被磨刀具z轴做螺旋包络运动，由极坐标像素平铺法转换为二值图像，然后结合数学形态学对二值图像开闭运算，提取螺旋槽端截形的边界廓形曲线。关于这一新方法的主要结论总结如下：

（1）本算法是以螺旋运动原理为基础，因此不仅适用于立铣刀螺旋槽的计算，也适用于各类圆柱螺旋槽加工计算。

（2）本算法无需求解接触线，避开了求解非线性方程，因此该方法解值稳定，无奇异解困扰。

（3）通过比较分析，PPM 法计算精度高，能够满足刀具实际加工中仿真计算的精度要求，并能提前预测加工刀具的重要参数和检验刀具结构的正确性。

（4）本方法基于像素图像的数学形态学，计算的数值解精度与点云数量直接相关，点云数量越多，计算精度越高，计算量就越大，常常影响计算的效率，但随着计算机计算性能的提高以及后期算法的优化，这一问题应该能够解决。