X80钢管道焊接致氢富集及热处理数值模拟

薛景宏, 白晨旭

(1. 东北石油大学 土木建筑工程学院, 黑龙江 大庆 163318;2. 东北石油大学 防灾减灾及防护工程重点实验室, 黑龙江 大庆 163318)

发展氢能既能缓解我国能源对外依存度高的问题,也能助力我国早日实现“双碳”战略目标。氢能被认为是最清洁的潜在能源,大力发展氢能也成为我国能源转型的迫切需求[1-2]。长距离管道输氢时,氢原子会进入金属材料内部,当金属材料中氢浓度过高时会引起氢脆,使管道材料发生塑性损伤甚至开裂。金属材料内部氢浓度过高的一个主要因素是管道焊接产生的残余应力。因此,研究管道焊接残余应力和应力诱导氢扩散规律对于管道输氢具有重要意义。

Gery等[3]建立了平板对接焊缝的二维和三维模型,比较发现三维模型的温度场更加符合实际。刁露阳等[4]采用高斯热源模型对管径为219 mm的X60钢管道进行了焊接模拟,分析了焊接温度场和应力场规律,但在建模时忽略了焊材的填充过程。刘维洋[5]采用双椭球热源模型对管径为1219 mm的X80钢管道进行焊接数值模拟,分析了管道内外表面残余应力场的分布规律,但该模拟仅将填充焊简化为一道。陈勇等[6]建立了304不锈钢管的二维环焊缝模型,分析了焊后热处理对残余应力的消除机制。蒋文春等[7]通过有限元软件对液化石油气球罐氢扩散的分布规律进行了模拟研究,发现在焊接残余应力作用下,氢向高应力区富集。Yan等[8]建立了X80管线钢焊接接头氢分布的三维模型,研究发现,提高预热温度和焊接热输入都可降低焊接接头中的氢浓度。目前,大口径管道多层焊接残余应力及氢扩散的模拟研究较少,尤其是通过焊后热处理降低焊接残余应力和氢富集的研究较少。鉴于此,笔者拟采用有限元软件Abaqus,建立含6层环焊缝管道模型,并进行模型验证。通过间接耦合方法进行温度场、应力场和氢扩散耦合分析,得出焊接残余应力及氢浓度的分布规律、静水应力和氢浓度关系以及热处理对焊接残余应力及氢富集的影响。

1 有限元模型的建立

1.1 有限元模型

X80钢含6层环焊缝管道的有限元模型见图1,管道长取1000 mm,圆心角取90°,管道外径为φ1219 mm,壁厚为18.4 mm,模型左端面为焊缝中心面,在焊缝处及附近网格加密,远离焊缝区域网格较稀疏,焊接工艺参考文献[9]。

1.2 材料参数

X80管线钢热物理性能参数见表1[8,10],其中ρ为密度,α为导热系数,Cp为比热容,k为线膨胀系数,σs为屈服强度,E为弹性模量,μ为泊松比,取0.3。除表1给出的特定温度下的物理参数值外,其余温度下的具体参数值通过插值法和外推法获取。

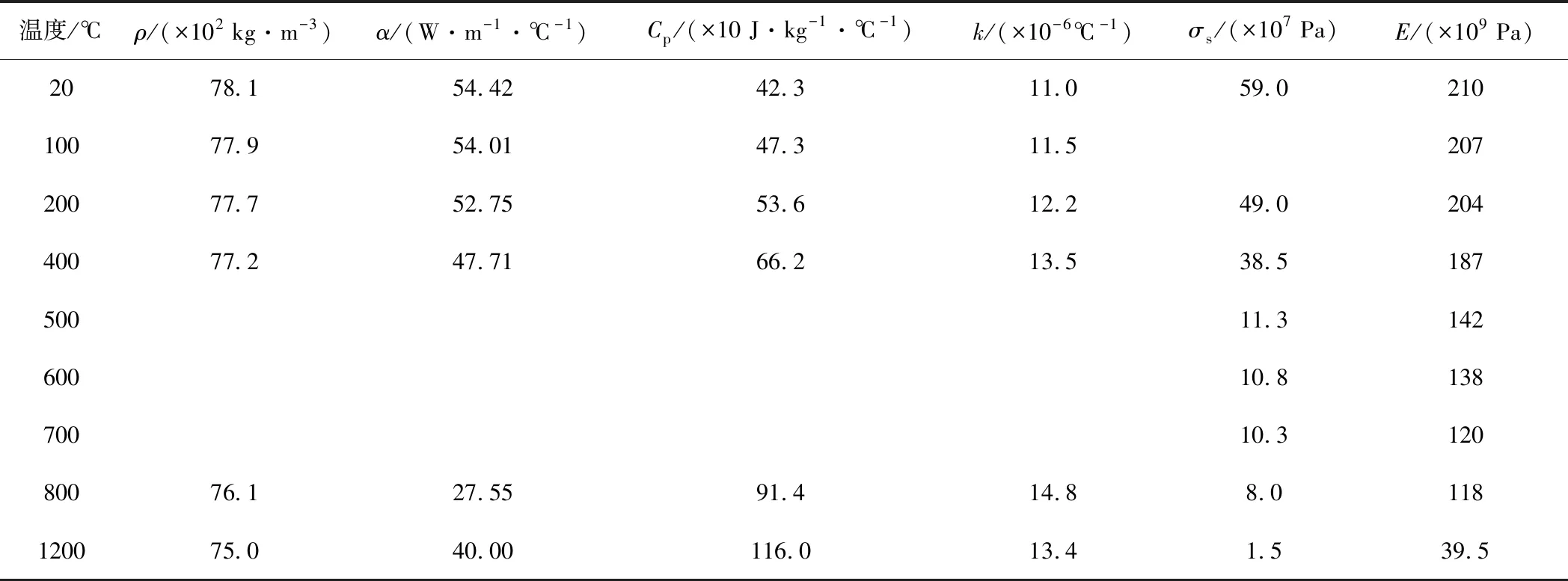
表1 X80管线钢的热物理性能参数[8,10]

1.3 边界条件

在热分析中,管道的初始温度为20 ℃,焊接时需考虑管道内外表面的对流散热和辐射散热,热辐射率取0.8,对流换热系数取25 W/(m2·℃),环境温度取20 ℃,焊接时的相对热效率η=0.9[9]。模型左端为焊缝中心面,与模型轴线平行的两个断面均为对称边界。

1.4 模型验证

Deng等[11]采用钨极气体保护焊对SUS304管进行焊接试验,并用应变片测量了焊接残余应力。本文为了验证焊接有限元模型与方法的准确性,按照Deng等[11]的试验建立了模型,并提取了管道外表面焊后轴向应力,对比分析如图2所示,可见有限元模拟得到的焊后轴向应力值与其试验测量值拟合度较高,从而验证了焊接有限元力学模拟的可靠性。

图2 X80钢管焊后轴向应力模拟值与试验值对比Fig.2 Comparison of simulation value and test value of axial stress of the X80 steel pipe after welding

2 焊接残余应力与热处理

管道焊缝和热影响区温度分布不均匀会产生较大的残余应力,因此应对管道进行焊后热处理,加热带应包含管道焊缝和热影响区,以及相邻的部分母材,焊缝每侧加热范围应不小于焊缝宽度的3倍,本研究对整个管道进行焊后热处理,将管道匀速升温至600 ℃,恒温6 h,然后匀速降温至20 ℃。

2.1 Mises等效应力分布

管道焊后不均匀的应力场是由不均匀的温度场所引起,图3所示为管道焊接完成后经历10 800 s自然风冷至室温时的等效残余应力云图。从模拟结果可以看出,等效应力主要集中在焊缝区以及相邻的热影响区内,其中外表面产生的等效应力要高于内表面,外表面的等效应力峰值达到580 MPa,内表面的等效应力峰值为417 MPa,外表面的等效应力峰值已接近管材的屈服强度。热处理后等效应力峰值降为167 MPa,降幅为71.2%,且应力分布更加均匀。

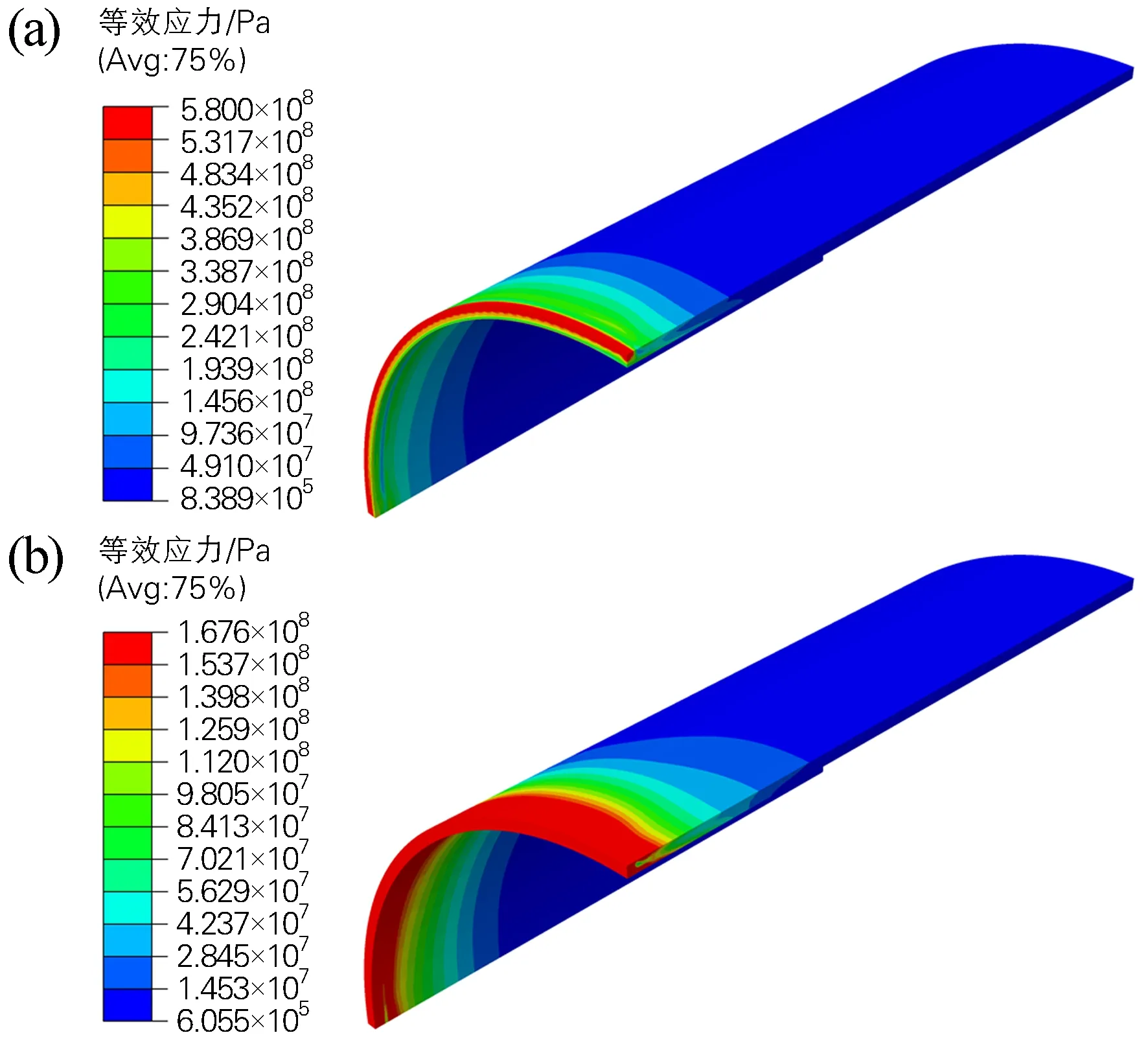
图3 X80钢管等效残余应力云图(a)热处理前;(b)热处理后Fig.3 Equivalent residual stress cloud of the X80 steel pipe(a) before heat treatment; (b) after heat treatment

2.2 管道外表面应力分布

从模型左端面(焊缝中心面)中点(距焊接起点45°位置),沿着与管轴平行方向提取外表面残余应力数据,得到焊后热处理前后外表面环向和轴向残余应力分布曲线,如图4所示。由图4(a)可以看出,在焊后热处理前,随着距焊缝中心面距离的增加,外表面环向残余拉应力先小幅度上升,在焊缝熔合线处达到最大值,然后迅速减小并转变为压应力,然后再缓慢降至0 MPa附近,环向拉应力和压应力峰值分别为623 MPa和165 MPa。在焊后热处理后,拉应力和压应力峰值分别降为190 MPa和31 MPa,降幅为69.5%和81.2%。从图4(b)可以看出,在焊后热处理前,外表面焊缝中心处表现为轴向残余压应力,随着距焊缝中心面距离的增加,压应力迅速下降并转变为拉应力,然后再缓慢降至0 MPa附近,拉应力峰值为277 MPa。在焊后热处理后,拉应力峰值降为183 MPa,降幅为33.9%。由此可见,经过焊后热处理,管道外表面环向和轴向焊接残余应力峰值均得到大幅下降。

图4 X80钢管外表面焊接残余应力(a)环向残余应力;(b)轴向残余应力Fig.4 Welding residual stress on outer surface of the X80 steel pipe(a) circumferential residual stress; (b) axial residual stress

2.3 管道内表面应力分布

从模型左端面(焊缝中心面)中点(距焊接起点45°位置),沿着与管轴平行方向提取内表面残余应力数据,得到焊后热处理前后内表面环向和轴向残余应力分布曲线,如图5所示。由图5(a)可以看出,在焊后热处理前,随着距焊缝中心面距离的增加,内表面环向拉应力迅速减小并转变为压应力,然后再逐渐降至0 MPa附近,环向拉应力和压应力峰值分别为413 MPa和322 MPa。焊后热处理后,拉应力和压应力峰值分别降为167 MPa和158 MPa,降幅为59.6%和50.9%。由图5(b)可以看出,在焊后热处理前,随着距焊缝中心面距离的增加,内表面轴向拉应力减小并转变为压应力,然后再逐渐降至0 MPa附近,压应力峰值为225 MPa,热处理后压应力峰值降为179 MPa,降幅为20.4%。由此可见,经过焊后热处理,管道内表面环向和轴向焊接残余应力峰值都均到大幅下降。

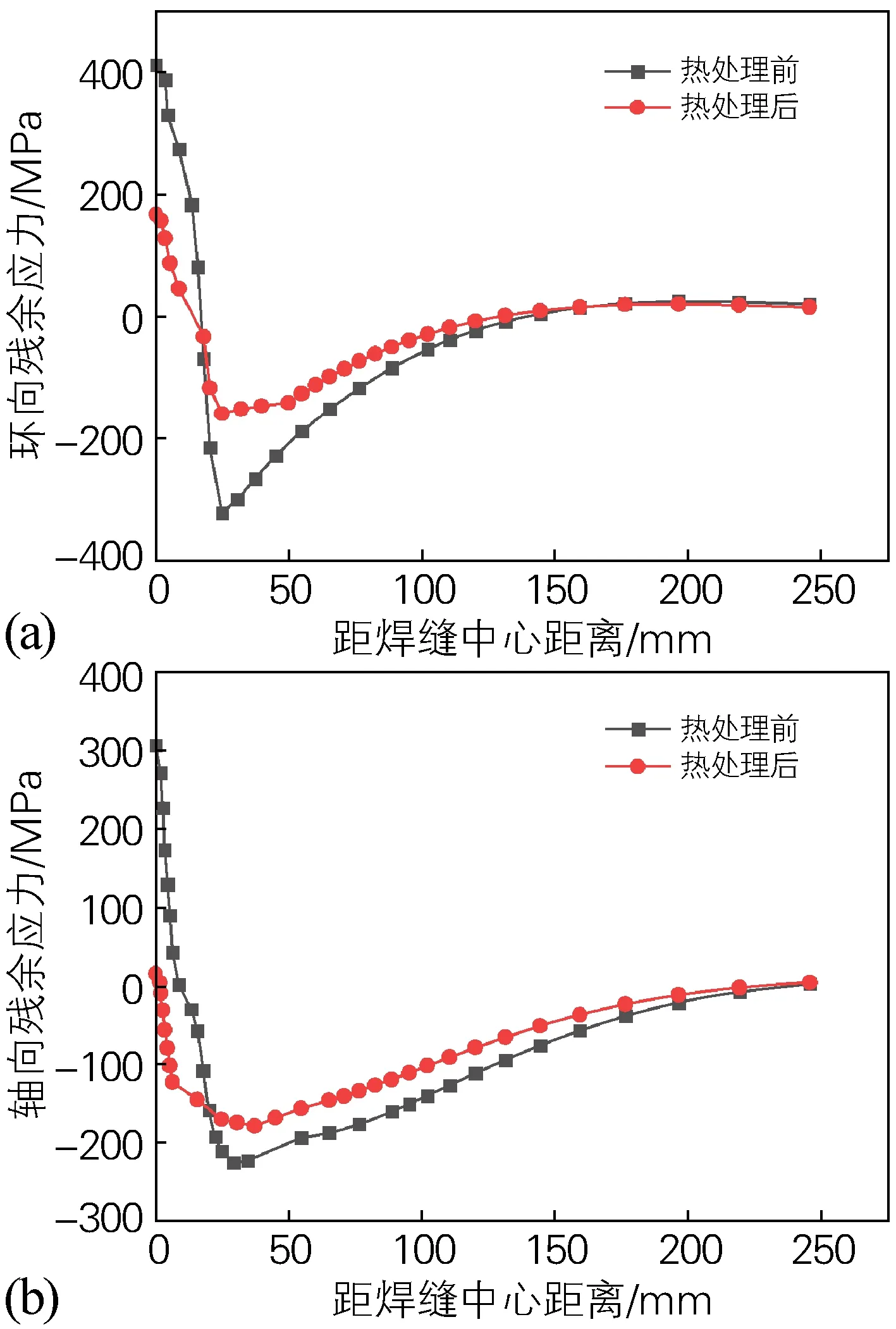
图5 X80钢管内表面焊接残余应力(a)环向残余应力;(b)轴向残余应力Fig.5 Welding residual stress on inner surface of the X80 steel pipe(a) circumferential residual stress; (b) axial residual stress

综上可知,X80管道内外表面在经过焊后热处理后,焊接残余应力得到了较大的释放,应力松弛效果明显。

3 静水应力与氢扩散

3.1 静水应力分布

静水应力为管道环向应力、轴向应力和径向应力的平均值。图6为热处理前焊缝附近的压力分布云图,其值为静水应力的负值,可以间接看出静水应力较高区域主要集中在第4、第5焊层交界处。为了更好地观察静水应力及氢浓度的分布规律,在焊缝处取路径P1和P2,定义P1位于焊缝中心面上,由管道内表面指向外表面,定义P2沿着管道轴向,距离管道内表面12 mm处(即第4、第5焊层交界处)。

图7为路径P1、P2上的静水应力分布。由图7(a)可知,沿路径P1,管材内的静水应力呈波动分布,热处理前静水应力在距离管道内表面12 mm处达到最大值347 MPa,热处理后的静水应力峰值降为109 MPa,降幅68.6%。从图7(b)可知,沿着路径P2,静水应力在热处理前呈单调降低分布,热处理后其接近直线分布。

3.2 氢扩散基本假设与氢浓度分布

本文在进行氢扩散分析时做出如下的基本假设:①不考虑焊缝处组织不均匀;②氢在管线钢中扩散时只以氢原子的形式进行,扩散至管道外结合成氢分子,氢浓度变为0;③忽略管线钢中的夹杂、微孔洞;④忽略管线钢冶炼时引入的氢,认为初始状态时管线钢内部的氢浓度为0;⑤扩散系数为各向同性。假设管道焊缝和母材区的氢扩散参数相同,根据文献[12],设管道内表面的吸附氢浓度为0.0235×10-6,管材的溶解度和氢扩散系数分别为4.797×10-11·Pa-1/2和3.302×10-6cm2/s。

图8(a)为无残余应力时管材的氢浓度分布,氢从管道内表面向外表面均匀扩散,沿着管道轴向的氢浓度值相等。图8(b, c)为有残余应力的管材氢浓度分布,可见未经热处理时氢会受静水应力梯度的影响,向静水应力高的第4、5焊层交界处进行富集,而经过热处理后管材的氢浓度分布与未经热处理时类似,但氢浓度值大幅度降低。

图8 X80钢管氢浓度分布云图(a)无残余应力;(b)热处理前的残余应力;(c)热处理后的残余应力Fig.8 Cloud maps of hydrogen concentration distribution of the X80 steel pipe(a) without residual stress; (b) with residual stress before heat treatment; (c) with residual stress after heat treatment

沿路径P1和P2进行氢浓度分析,如图9所示。由图9(a)可见,在无残余应力时,氢浓度由管道内表面向外表面呈直线递减分布,氢浓度最大值为0.0235×10-6,位于管道内表面。存在焊接残余应力时,热处理前的氢浓度在距离管道内表面12 mm处达到最大值0.0605×10-6。热处理后氢浓度在管道内表面处达到最大值0.0235×10-6,氢浓度在距管道内表面12 mm处出现与最大值接近的峰值(0.0203×10-6)。因此,存在焊接残余应力时,热处理前氢浓度的峰值是无残余应力时的2.6倍,且氢浓度的峰值位置由管道内表面转移到了距离内表面12 mm处;热处理后此位置氢浓度大幅下降,较热处理前下降66.4%,同时最大氢浓度位置转移到管道内表面。

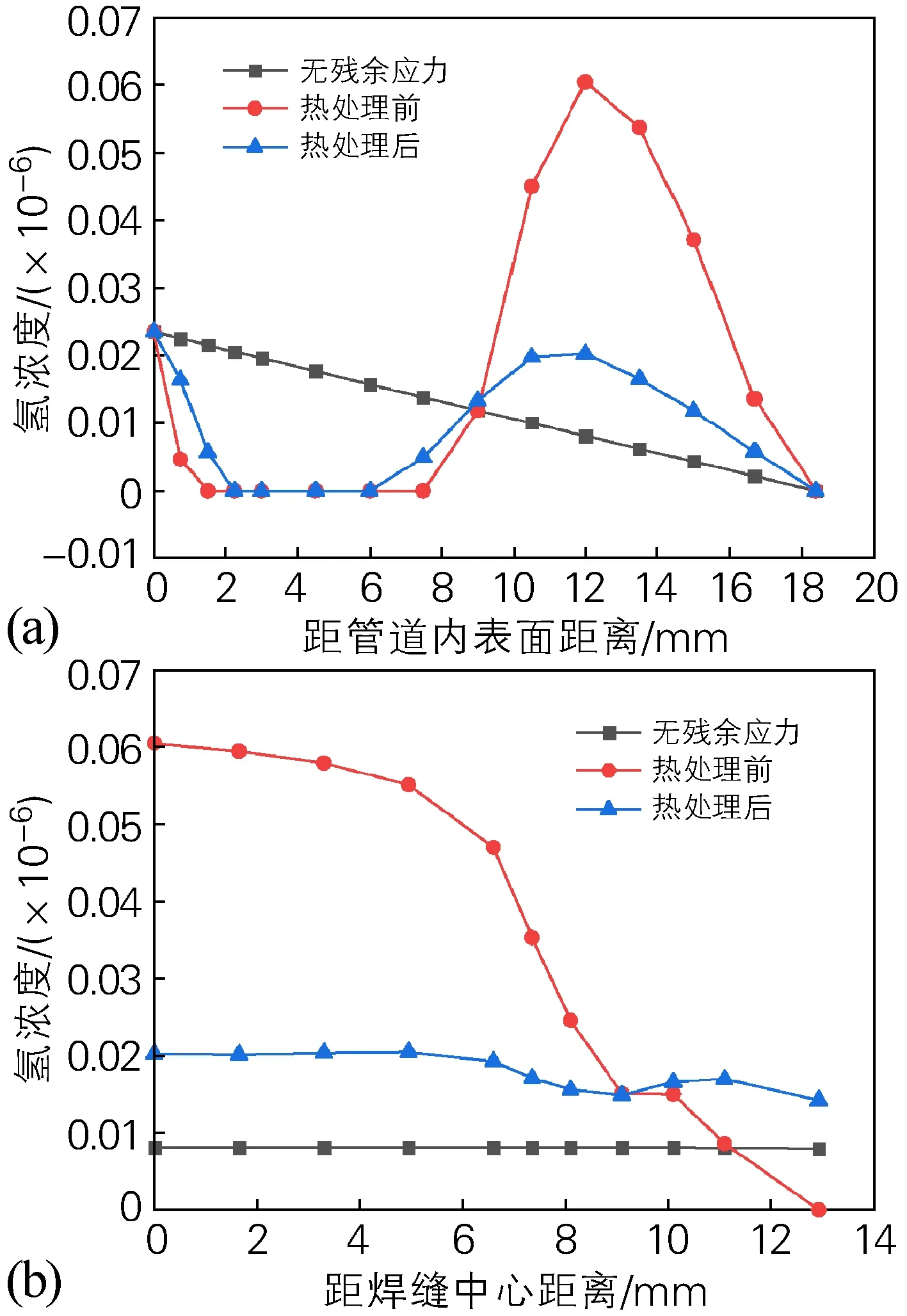
图9 X80钢管沿路径P1(a)和P2(b)的的氢浓度分布Fig.9 Hydrogen concentration distribution along path P1(a) and path P2(b) of the X80 steel pipe

由图9(b)可见,无残余应力时,焊缝及其毗邻区域内氢浓度沿着路径P2方向的分布呈直线型分布,浓度值较小,为0.0081×10-6。存在焊接残余应力时,热处理前的氢浓度随着距焊缝中心面距离的增加由最大值0.0605×10-6快速下降。热处理后氢浓度在距离焊缝中心面5 mm范围内接近直线型分布,浓度值约为0.020×10-6,之后出现一定的波动。由此可见,热处理后焊缝及其毗邻区域氢浓度明显下降(66.9%),且分布更加均衡。

对比图7和图9可知,氢浓度的分布规律与静水应力的分布规律相似,氢富集于高静水应力区域,可以认为静水应力是驱动氢富集的因素,而且热处理可以有效降低氢富集浓度。

4 结论

1) 焊缝区Mises等效应力峰值高达580 MPa,已接近X80钢管材屈服强度,管道外表面的等效应力高于内表面。热处理后焊缝区Mises等效应力峰值降为167 MPa,且焊缝处应力集中明显缓解,应力分布更加均匀。

2) 随着距焊缝中心面的距离增大,管道内、外表面的环向残余应力和管道内表面的轴向残余应力均由拉应力迅速减小并转变为压应力,然后逐渐降至0 MPa附近,管道外表面轴向残余应力由压应力迅速减小并转变为拉应力,然后逐渐减小至0 MPa附近。热处理后残余应力峰值都大幅降低。

3) 热处理前,静水应力沿管材径向由内表面至外表面呈波动分布,沿管轴向随距焊缝中心距离的增加呈下降分布,很快趋于平稳,静水应力峰值347 MPa出现在距离管道内表面12 mm的第4、第5焊层交界处,热处理后静水应力峰值降为109 MPa。

4) 静水应力与氢浓度分布规律相同,驱动氢扩散并可表征氢富集程度。热处理前径向氢浓度在距离管道内表面12 mm处达到最大值0.0605×10-6,热处理后降为0.0203×10-6。热处理可显著降低输氢管道氢富集浓度,从而减少焊缝处氢脆现象的发生。