求简单多面体外接球的两妙招

田向红

摘要：在高三复习备考中，有很多求简单多面体外接球表面积、体积的问题，这类题最终的落脚点就是求外接球的半径，本文中结合历年高考试题，重点介绍常用的补形法和交轨法两种妙招.

关键词：补形法；交轨法；多面体的外接球；立体几何

简单多面体外接球问题是高考中的重点和难点问题，近年来在高考考查中呈上升的趋势，涉及到的题型主要是求多面体外接球的表面积、体积以及球心到指定截面的距离等问题.

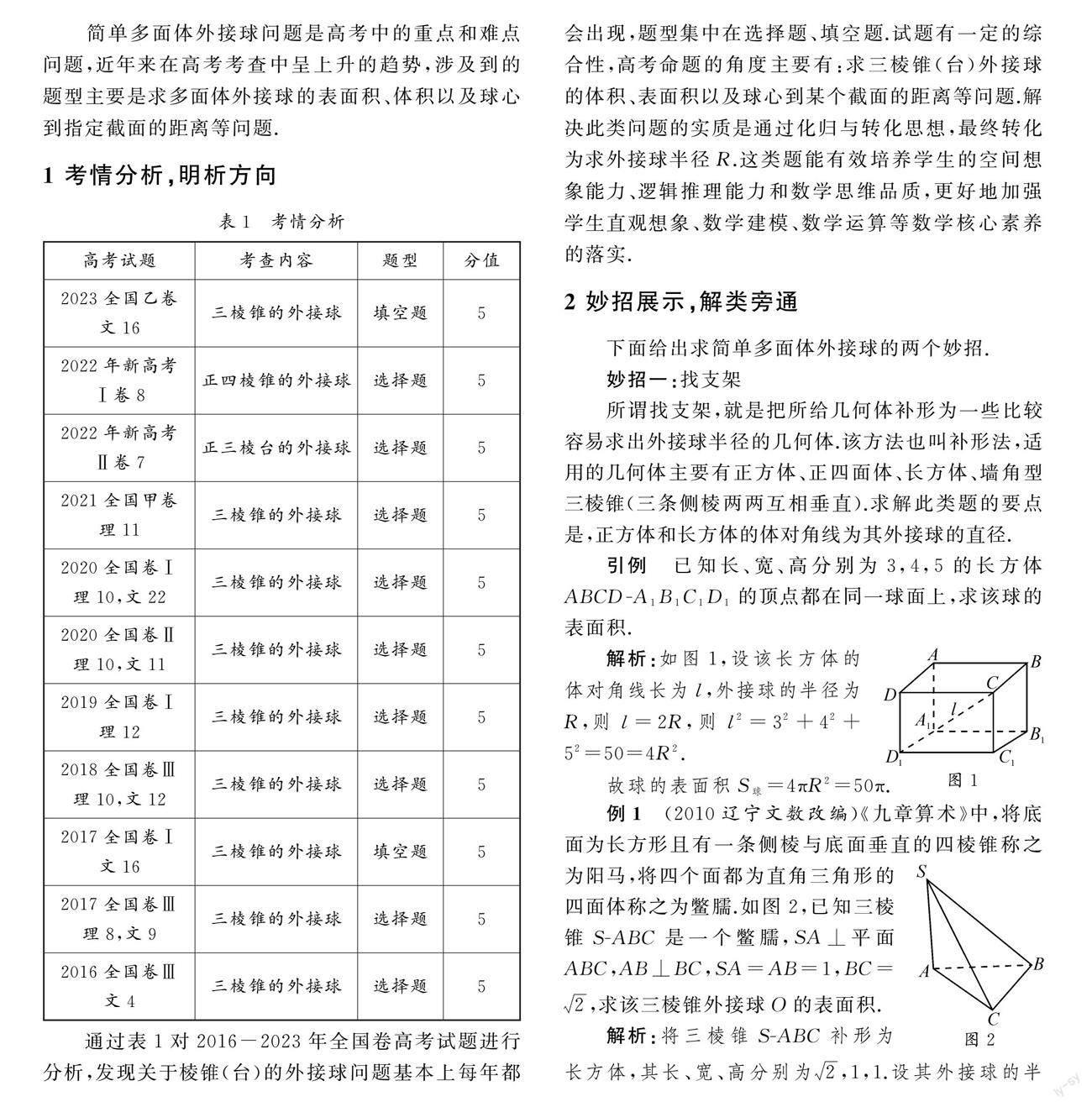
1 考情分析，明析方向

通过表1对2016-2023年全国卷高考试题进行分析，发现关于棱锥（台）的外接球问题基本上每年都会出现，题型集中在选择题、填空题.试题有一定的综合性，高考命题的角度主要有：求三棱锥（台）外接球的体积、表面积以及球心到某个截面的距离等问题.解决此类问题的实质是通过化归与转化思想，最终转化为求外接球半径R.这类题能有效培養学生的空间想象能力、逻辑推理能力和数学思维品质，更好地加强学生直观想象、数学建模、数学运算等数学核心素养的落实.

2 妙招展示，解类旁通

下面给出求简单多面体外接球的两个妙招.

妙招一：找支架

所谓找支架，就是把所给几何体补形为一些比较容易求出外接球半径的几何体.该方法也叫补形法，适用的几何体主要有正方体、正四面体、长方体、墙角型三棱锥（三条侧棱两两互相垂直）.求解此类题的要点是，正方体和长方体的体对角线为其外接球的直径.

引例 已知长、宽、高分别为3，4，5的长方体ABCD-A1B1C1D1的顶点都在同一球面上，求该球的表面积.