影响环形聚能装药侵彻能力的单因素分析及正交优化设计

吴海军,王可慧,柯 明,杨 慧,李 明,段 建,张庆明

(1. 北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2. 西北核技术研究所,西安 710024)

环形聚能装药是一种特殊结构的线性聚能装药,具有体积小、破甲能力强及侵彻孔径大的特点,能实现对靶板的大口径开孔,其独特的作用效果受到了国内外学者的关注。Chick等[1]将线性聚能装药弯曲为环形形成环形射流,但实验中发现这种方法形成的射流不稳定。针对环形聚能装药的非对称性导致射流内偏的现象,根据等动量守恒原则,吴成等[2]提出了内壁加厚或外壁减薄使药型罩内外壁质量相等的质量补偿设计方法;王成等[3]设计的W型聚能装药不仅内外壁质量相等,且对应的装药质量也相等;段嘉庆等[4]使内外壁顶部厚度相同,外壁底部厚度减为顶部2/3,内壁底部厚度稍减,确保内外壁压垮同步,在一定程度上克服了环形射流易偏斜及断裂的问题。为进一步提升环形射流的侵彻能力,王伟力和李永胜等[5-7]采用数值模拟方法对环形聚能装药的药型罩材料、药型罩锥角、起爆控制、装药形状及炸高等因素分别进行了研究,指出60°锥角及柱锥状装药的环形聚能装药对靶板的切割效果最理想。吴建宇等[8]、吴海军等[9]和何降润等[10]分别研究了炸高、环形同步起爆点数、壳体厚度及材料(铝、钢或钨)对环形射流成型和侵彻深度的影响;王成等[11]分析了起爆环直径和装药长径比对铝合金环形聚能装药成型过程的影响。

如前所述,影响环形射流成型和侵彻性能的因素很多,如药型罩、装药、起爆方式及壳体等,针对单一因素的研究并不能取得理想效果。近年来,许多学者采用多种优化设计方法,开展了环形聚能装药的优化设计。吴国东等[12]设计了一种弧锥结合的变壁厚环形药型罩结构,基于灰度理论对圆弧曲率半径、锥角、罩顶厚、装药高度及壳体厚度等因素进行了灰关联分析,找出了影响侵彻能力的最主要因素。傅磊[13]等采用正交试验方法对环型聚能装药结构进行了优化设计,得到了药型罩开口角度、药型罩壁厚、装药高度及炸高的影响规律。马焱等[14]采用灰度理论对正交实验数据进行了分析,然后应用基于支持向量机回归、粒子群优化及遗传算法等参数寻优算法的支持向量机网络回归模型对灰色关联度进行预测,实现了环型聚能装药侵彻靶板能力的预测。徐文龙等[15]设计了一种带有隔板和辅助装置的环形聚能装药,基于正交试验方法,给出了药型罩壁厚、药型罩曲率半径、聚焦装置锥角、喷孔直径及壳体厚度对射流头部轴向及径向速度的影响及优化参数。刘宏杰等[16]设计了一种双锥罩环形聚能装药,采用灰度理论研究了不同结构参数(双锥罩上锥角、壁厚、罩高及上锥罩高占比)对环形射流头部速度和长度的影响,获得了优化的双锥罩设计参数。杨世全等[17]采用正交试验方法研究了药型罩壁厚、装药高度和起爆直径对等壁厚球缺药型罩杆式射流成型和侵彻性能的影响。

总之,环形射流的研究起步较晚,传统聚能射流的设计方法和经验不能直接应用于环形聚能装药的设计,采用正交试验和灰度理论等方法对其进行多变量联合优化,为环形聚能装药的设计和应用提供了更加直接的指导。本文利用显示动力学有限元软件LS-DYNA,分析得到了药型罩锥角、药型罩厚度、装药高度和炸高4个因素对侵彻能力的影响规律,以环形聚能射流对钢板的侵彻能力为指标,采用正交试验方法对环形聚能装药进行了优化设计,改善了射流成型,增强了侵彻能力。

1 计算模型

1.1 环形聚能装药初始结构

图1为本文设计的环形聚能装药及药型罩部分的初始结构截面示意图。由图1(a)可见,环形聚能装药结构参数为:壳体厚度a=2 mm,装药高度H=160 mm(2.00d);由图1(b)可见,药型罩结构参数为:药罩口径d=80 mm,锥角α=60°,壁厚δ=4 mm(0.05d),装置外侧半径Router=200 mm,中空部分半径Rinner=120 mm,药型罩锥顶环形半径R0=160 mm。起爆方式为环向8点同步起爆,初始炸高h取80 mm(1.00d)。

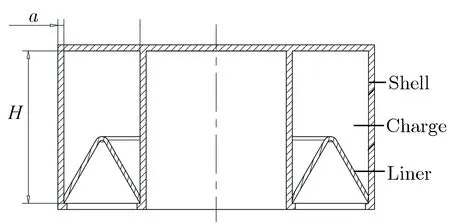
(a) Annular shaped charge

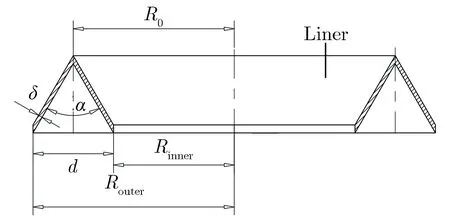
(b) Liner图1 环形聚能装药及药型罩初始结构截面示意图Fig.1 Schematic diagram of the initial structure of annular shaped charge and the liner

1.2 几何模型

环形聚能装药及靶板几何模型如图2所示,主要由药型罩、装药、壳体、空气及靶板5部分组成。其中,靶板为100 mm厚的921A船用钢板。壳体和靶板采用Lagrange单元,药型罩、装药和空气采用ALE单元,它们之间的相互作用采用流固耦合算法。使用Solid164实体单元对模型进行划分,将药型罩、装药和空气划分为共节点单元,用空气网格包围药型罩和装药,并延伸至射流运动的整个区域。为空气网格的上下表面及侧面添加无反射边界,模拟无限条件。靶板侧面固定支撑,被侵彻区域局部网格加密,设定网格特征尺寸为2 mm,匹配药型罩网格,提高计算精度。

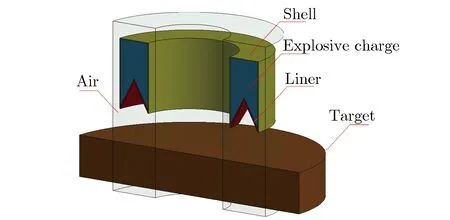
图2 环形聚能装药及靶板几何模型Fig.2 Geometric model of the annular shaped charge and the target

1.3 材料模型及参数

药型罩材料为无氧紫铜,壳体材料为45#钢,靶板材料为921A钢,均采用Johnson-Cook材料模型和Gruneisen状态方程来描述材料在动力学作用下的响应行为。装药为Octol炸药,采用HIGH_EXPLOSIVE_BURN本构方程,状态方程为JWL(Jones-Wilkins-Lee)。对于多物质ALE算法,需建立覆盖整个侵彻体飞行区域的空气网格。空气采用NULL本构方程,状态方程由LINEAR_POLYNOMIAL模型描述。主要模型参数如表1-表3所列。

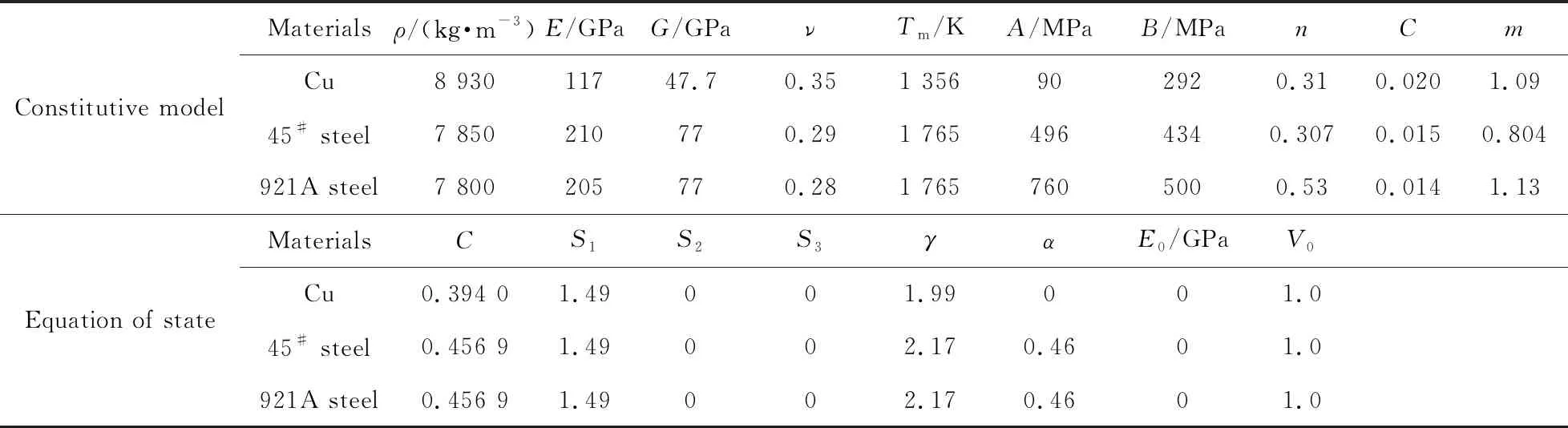
表1 紫铜、45#钢和921A钢的材料模型参数[18-19]Tab.1 Material parameters of red cooper, 45# steel, and 921A steel[18-19]

表2 Octol炸药的材料模型参数[18]Tab.2 Material model parameters of Octol explosive[18]

表3 空气的材料模型参数Tab.3 Material model parameters of air

2 影响环形聚能装药侵彻能力的单因素分析

选择药型罩锥角、药型罩厚度、装药高度及炸高4个因素为研究对象,通过数值模拟找出这些因素对环形聚能装药侵彻能力的影响规律,为进一步的优化设计提供参考。

2.1 药型罩锥角的影响

其他参数同初始方案保持一致,分别对药型罩锥角α为40°, 50°, 60°, 70°, 80°, 90°, 100°, 110°, 120°的环形聚能装药侵彻钢靶进行数值仿真,得到不同药型罩锥角的环形聚能装药对靶板侵彻的模拟结果,如图3所示。侵彻深度随药型罩锥角的变化关系如图4所示。由图3和图4可见:当药型罩锥角小于90°时,侵彻深度随锥角的增大而增大;当药型罩锥角大于90°时,侵彻深度随锥角的增大而减小;侵彻深度的极大值出现在90°锥角附近;当药型罩锥角为80°, 90°, 100°时,在弹坑底部外侧出现明显的剪切破坏,剩余靶板几乎被剪断。

(a) α=40°

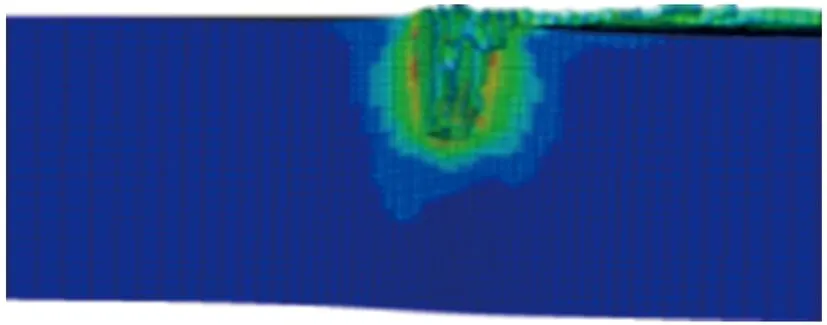
(b) α=50°

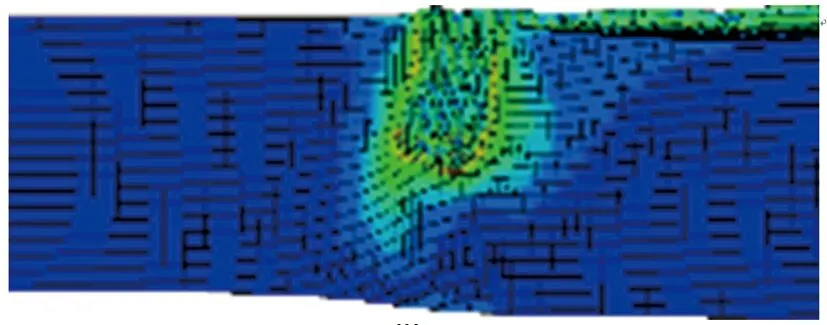
(c) α=60°

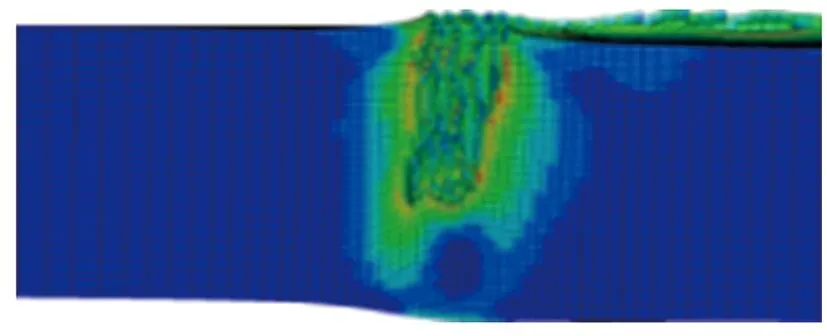
(d) α=70°

(e) α=80°

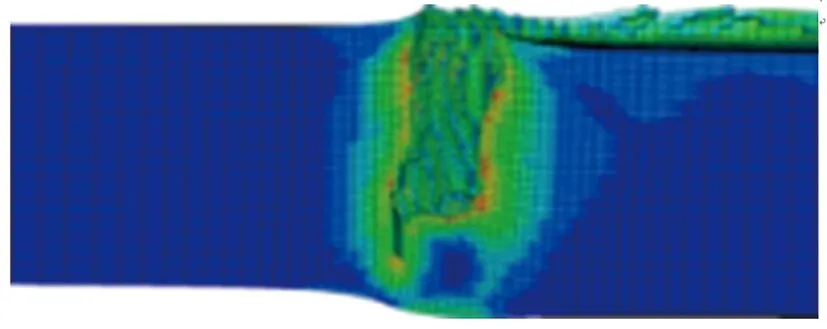
(f) α=90°

(g) α=100°

(h) α=110°

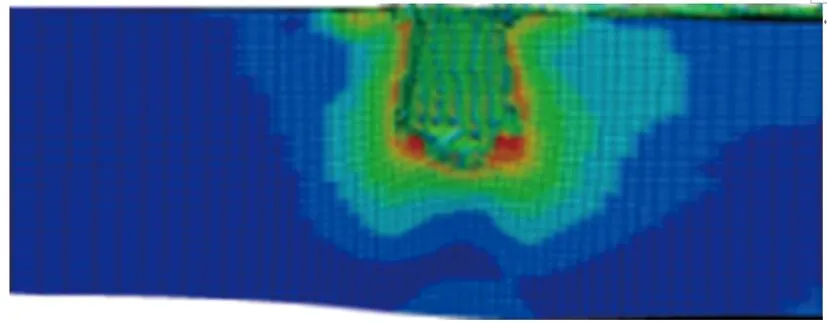
(i) α=120°图3 不同药型罩锥角的环形聚能装药对钢靶侵彻的模拟结果Fig.3 Simulation results of the annular shaped charge penetrating steel target with different liner cone angles

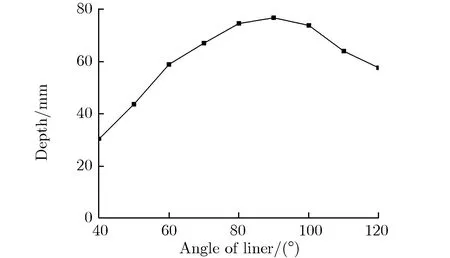
图4 侵彻深度随药型罩锥角的变化关系Fig.4 Penetration depth vs. the cone angle of liner

2.2 药型罩厚度的影响

其他参数同初始方案保持一致,分别对药型罩厚度δ为0.02d(1.6 mm),0.03d(2.4 mm),0.04d(3.2 mm),0.05d(4.0 mm),0.06d(4.8 mm),0.07d(5.6 mm),0.08d(6.4 mm),0.09d(7.2 mm),0.10d(8.0 mm)的环形聚能装药侵彻钢靶进行了数值仿真。不同药型罩厚度的环形聚能装药对靶板侵彻的模拟结果如图5所示。侵彻深度随药型罩厚度的变化关系如图6所示。

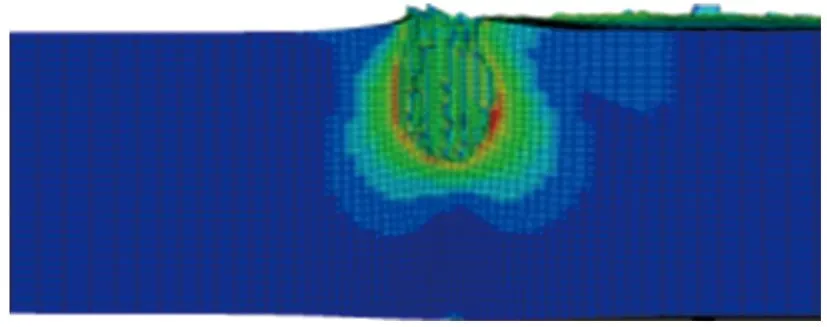
(a) δ=0.02d

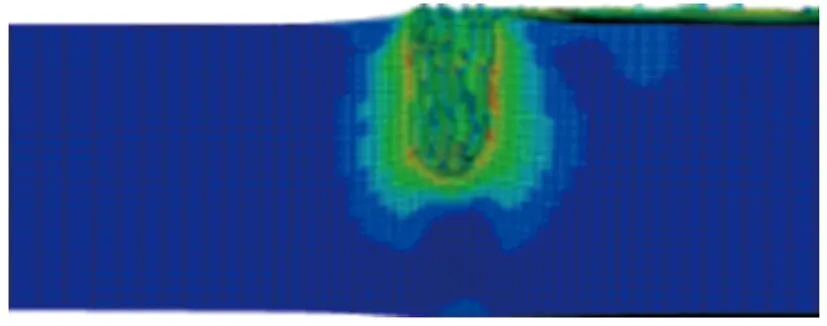
(b) δ=0.03d

(c) δ=0.04d

(d) δ=0.05d

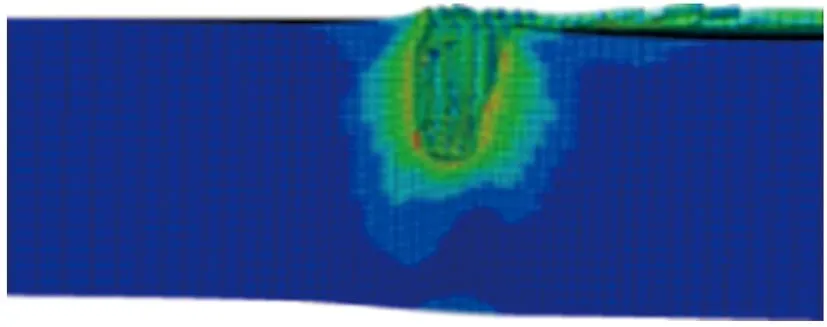
(e) δ=0.06d

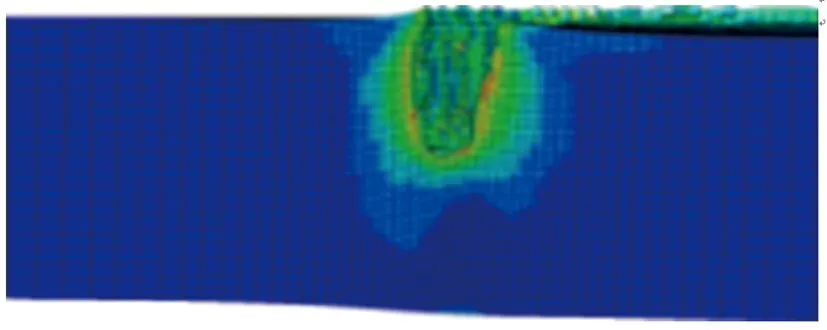
(f) δ=0.07d

(g) δ=0.08d

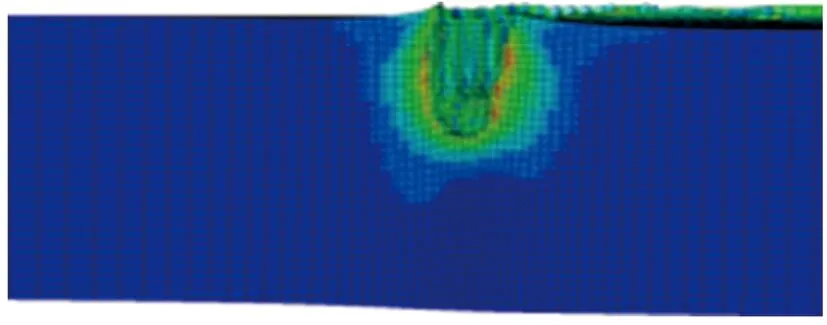
(h) δ=0.09d

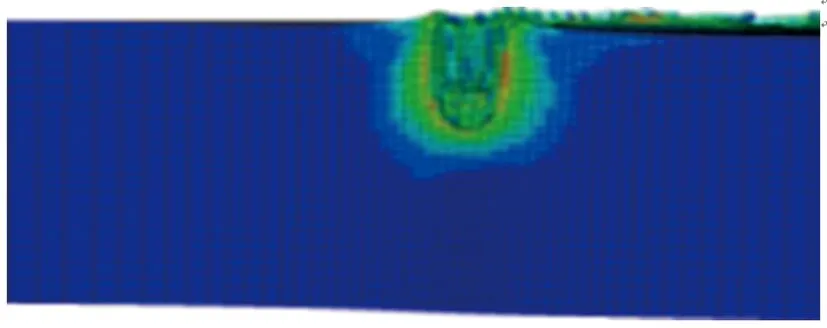
(i) δ=0.10d图5 不同药型罩厚度的环形聚能装药对钢靶侵彻的模拟结果Fig.5 Simulation results of the annular shaped chargepenetrating steel target with different liner thickness

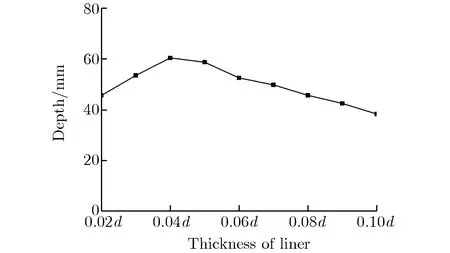
图6 侵彻深度随药型罩厚度的变化关系Fig.6 Penetration depth vs. the thickness of liner

由图5和图6可见,当药型罩厚度为0.02d～0.04d时,侵彻深度随药型罩厚度的增加而逐渐增加;当药型罩厚度大于0.04d时,侵彻深度又随药型罩厚度的增加而逐渐减小;侵彻深度的极大值出现在0.04d附近。这是因为单纯增加药型罩厚度可增加射流的质量,但射流速度会随之降低,射流有效能量并不能增加,因此在一定范围内增加药型罩厚度可提高侵彻深度,当药型罩厚度过大并无益处。

2.3 装药高度的影响

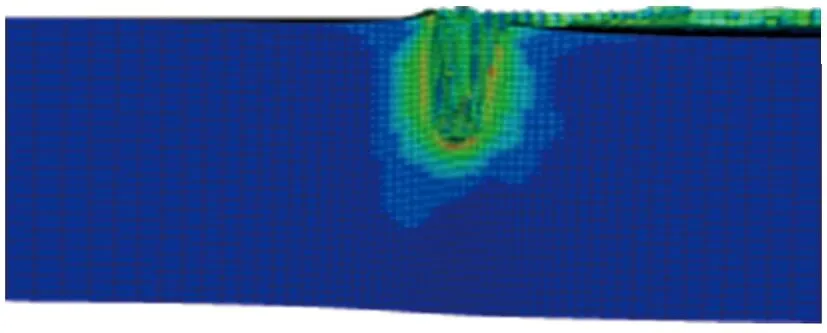
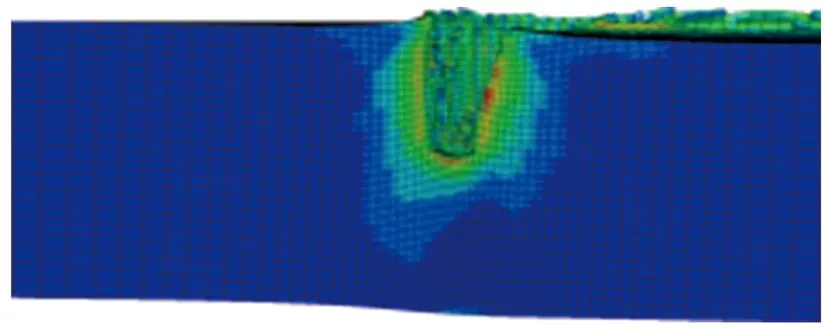
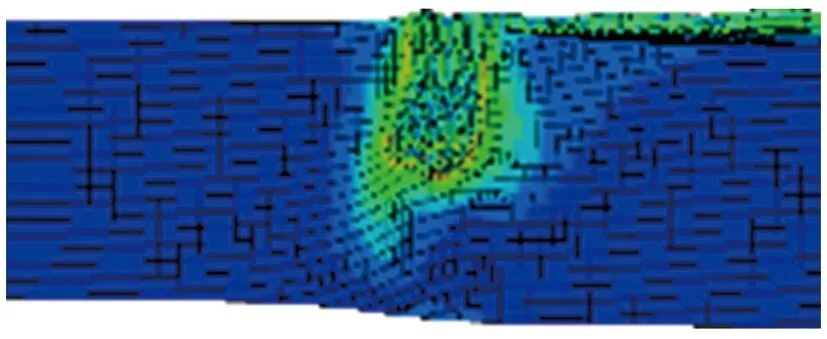
其他参数同初始方案保持一致,分别对装药高度H为1.00d(80 mm),1.25d(100 mm),1.50d(120 mm),1.75d(140 mm),2.00d(160 mm),2.25d(180 mm),2.50d(200 mm)的环形聚能装药侵彻钢靶进行了数值仿真。不同装药高度的环形聚能装药对靶板侵彻的模拟结果如图7所示。

(a) H=1.00d

(b) H=1.25d

(c) H=1.50d

(d) H=1.75d

(e) H=2.00d

(f) H=2.25d

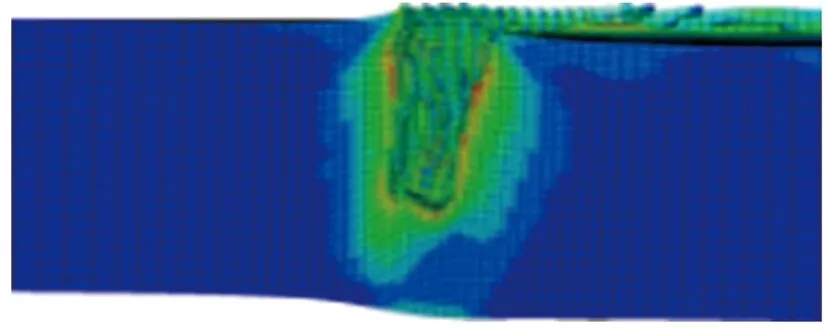
(g) H=2.50d图7 不同装药高度的环形聚能装药对钢靶侵彻的模拟结果Fig.7 Simulation results of the annular shaped charge penetrating steel target with different loading heights

图8为侵彻深度随装药高度的变化关系。由图7和图8可见,当装药高度为1.00d～2.50d时,弹坑深度随装药高度的增加而逐渐增加,但增加幅度逐渐减小。这是因为增加装药高度也即增加装药量,射流能量随之增加,在一定范围内增加装药高度可提高侵彻深度,但单纯依靠增加装药高度来提高侵彻深度并不经济,降低了炸药能量的利用率。

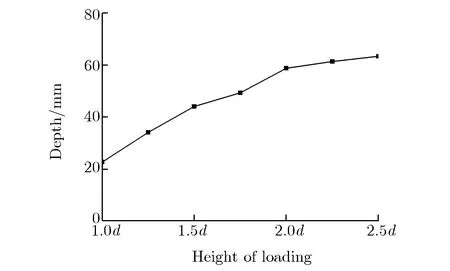
图8 侵彻深度随装药高度的变化关系Fig.8 Penetration depth vs. the height of loading

2.4 炸高的影响

其他参数同初始方案保持一致,分别对炸高h为0.50d(40 mm),0.75d(60 mm),1.00d(80 mm),1.25d(100 mm),1.50d(120 mm),1.75d(140 mm),2.00d(160 mm)时,环形聚能装药侵彻钢靶进行了数值仿真。不同炸高时环形聚能装药对靶板侵彻的模拟结果如图9所示。

(a) h=0.50d

(b) h=0.75d

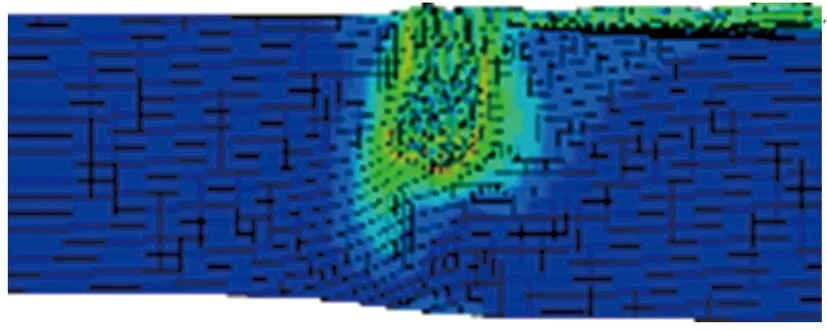
(c) h=1.00d

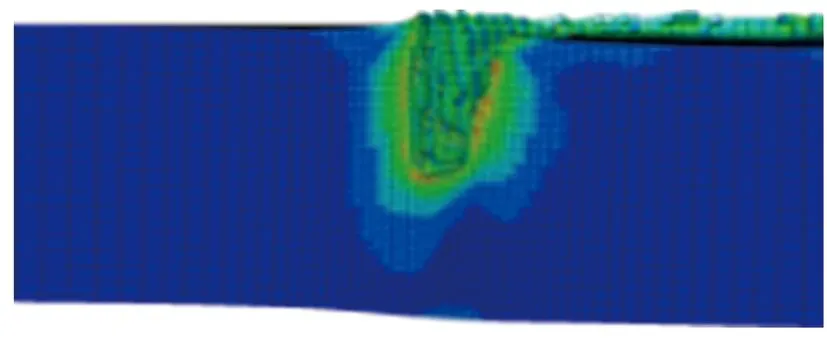
(d) h=1.25d

(e) h=1.50d

(f) h=1.75d

(g) h=2.00d图9 不同炸高时环形聚能装药对钢靶侵彻的模拟结果Fig.9 Simulation results of the annular shaped chargepenetrating steel target with different burst heights

图10为侵彻深度随炸高的变化关系。

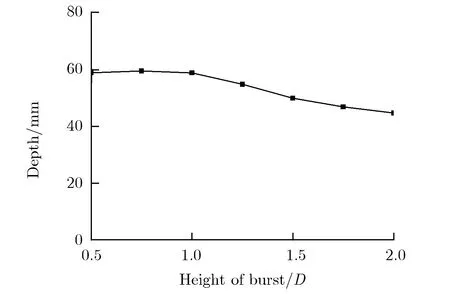
图10 侵彻深度随炸高的变化关系Fig.10 Penetration depth vs. the height of burst

由图9和图10可见,炸高为0.50d～1.00d时,侵彻深度变化幅度不大;炸高大于1.00d时,侵彻深度随炸高的增大而减小;侵彻深度的极大值出现在0.75d附近。这是因为在一定范围内增加炸高有利于射流在成型过程中充分伸展,增大射流长径比,有利于提高侵彻深度,但炸高过大时,射流在运动过程中易发生断裂,降低侵彻能力。

3 环形聚能装药正交试验设计

由第2节分析可知,影响环形聚能装药侵彻能力的因素较多,规律各不相同,且这些参数的影响不是相互独立的,针对单一变量的优化难以确定最佳方案,环形聚能装药结构设计过程中需进行多变量联合优化,才能有效提高环形射流的侵彻能力。对药型罩锥角、药型罩厚度、装药高度及炸高这4个因素,每个因素4个变化水平的优化问题而言,若采用单因素轮换的方法,将有44共256种组合,试验数量庞大,效率较低。

正交试验设计又称正交设计或多因素优选设计,是合理安排、科学分析各试验因素的一种有效数理统计方法。它借助正交表这一工具,从众多的试验条件中挑选出部分具有代表性的试验点,科学安排试验,然后对试验结果进行综合比较和统计分析,找出各因素水平的最佳组合,从而得到最优或较优的试验方案。正交试验设计的特点是用不太多的试验次数,就能找出试验因素的最佳水平组合,了解试验因素的重要程度及交互作用情况,减少试验的盲目性,避免资源浪费[20]。

3.1 正交试验方案

在开展环形聚能装药的优化设计过程中,有的文献以射流轴向速度和径向速度作为优化指标[15],有的以轴向/径向速度和密实度作为优化指标[12],有的以射流速度和长度作为指标[16],也有的以环形射流穿靶时间及剩余速度作为优化指标[13],但环形聚能装药的侵彻深度不仅和射流的轴向和径向速度有关,射流的形状(如截面积及长径比等)也会对侵彻深度产生影响。因此,选用侵彻深度Xij作为试验指标更有针对性。

影响环形聚能装药侵彻能力的因素主要包括:药型罩材料、形状、锥角、厚度;装药性能、高度;壳体厚度;起爆方式;炸高等因素。其中,药型罩的材料、形状,装药种类、性能,起爆方式均已选定,不在本次优化范围内。药型罩口径主要受总体参数制约,壳体厚度对侵彻深度的影响较小,暂不考虑。选定药型罩锥角α、药型罩厚度δ、装药高度H、炸高h共4个因素作为试验因素,分别记作A,B,C,D,每个因素取4个参数值。选择正交表L16(45),正交试验方案如表4所列。

表4 正交试验方案Tab.4 Orthogonal experiment scheme

3.2 正交试验结果分析

3.2.1 极差分析

针对正交试验方案中的参数组合进行16次的数值仿真,计算出不同条件下环形聚能装药的侵彻深度。正交试验结果的极差分析如表5所列。

(1) 确定因素的主次顺序

根据表5中极差Rj的大小,可判断各因素对试验指标影响的主次顺序。药型罩锥角因素的极差最大,药型罩厚度因素的极差最小,各因素主次关系为:药型罩锥角>炸高>装药高度>药型罩厚度。

(2) 确定试验因素的优水平和优组合

极差分析中所得到的最优组合并不在正交试验方案中,为考察优化结果,重新计算得到侵彻深度为72.88 mm,可知其侵彻能力确实高于表中其他参数组合方案。

3.2.2 方差分析

方差分析的基本思路是将数据的总变异分解为试验因素引起的变异和偏差引起的变异,从统计角度量化各因素对试验指标的影响程度,判断各个因素的作用是否显著。正交试验结果的方差分析如表6所列。

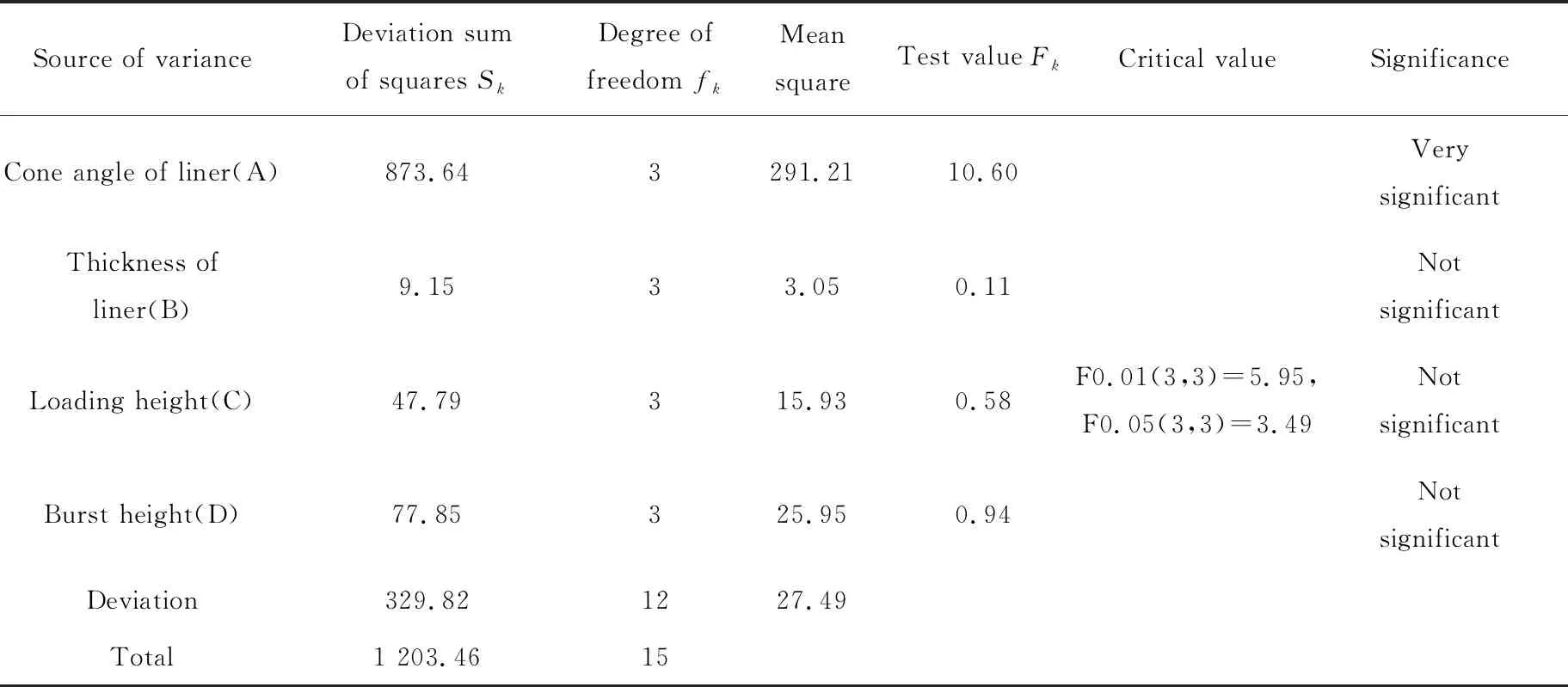
表6 正交试验结果的方差分析结果Tab.6 Variance analysis of orthogonal experiment results

方差分析结果从统计角度量化了各因素对环形聚能装药侵彻深度的影响,由表6可知,在所选因素及所选水平条件下,药型罩锥角对侵彻深度的影响非常显著,而药型罩厚度、装药高度及炸高的影响相对较小。

3.3 对药型罩锥角的进一步优选

通过正交试验设计的方法,得到了各因素的优化水平组合:药型罩锥角α为100°,药型罩厚度δ为0.05d,装药高度H为2.00d,炸高h为1.25d。同时,由第3.2节分析可知药型罩锥角对侵彻深度具有非常显著的影响,而正交试验设计中锥角的变化间隔较大。因此保持其他参数不变,对药型罩锥角α为80°, 85°, 90°, 95°, 100°的情况进行数值模拟,对药型罩锥角进行进一步优选。图11为侵彻深度随细化药型罩锥角变化关系。

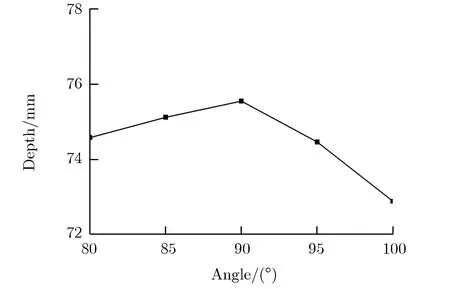
图11 侵彻深度随细化药型罩锥角变化关系Fig.11 Penetration depth vs. the refined cone angle of liner

由图11可见,当药型罩锥角为80°～90°时,侵彻深度随药型罩锥角的增加而略有增加,但增加幅度不大;当药型罩锥角大于90°后,侵彻深度随药型罩锥角的增加而明显减小;侵彻深度在药型罩锥角为90°时达到极大值。因此,最终优化方案选择药型罩锥角为90°。

优化方案侵彻深度计算结果如表7所列。由表7可知,初始方案的侵彻深度为0.66d,而正交试验方案的侵彻深度为0.91d,经过进一步优选药型罩锥角之后,侵彻深度可达0.94d,与初始方案相比,提高了约43%,优化效果明显。

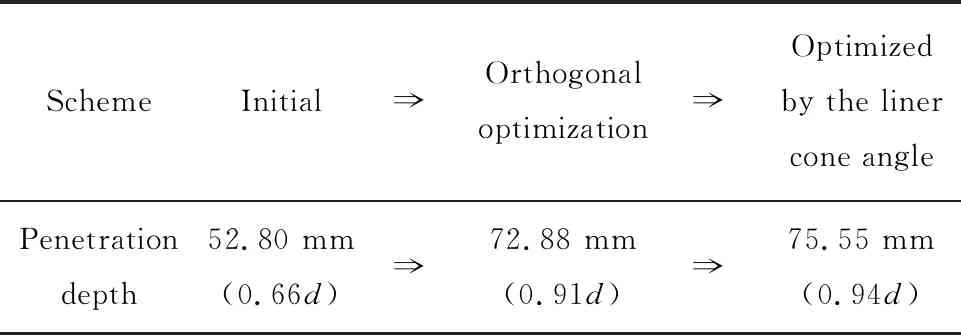
表7 优化方案侵彻深度计算结果Tab.7 Calculation results of penetration depth for the optimization schemes

4 结论

通过对影响环形聚能装药侵彻能力的单因素分析及正交试验设计,可得到以下结论:

(1) 药型罩锥角、药型罩厚度和炸高对侵彻能力的影响非单调变化。当药型罩锥角为40°～120°时,侵彻深度的极大值出现在90°附近;当药型罩锥角小于90°时,侵彻深度随药型罩锥角的增大而增大;当药型罩锥角大于90°时,侵彻深度随药型罩锥角的增大而减小。当药型罩厚度为0.02d～0.10d时,侵彻深度的极大值出现在0.04d附近;当药型罩厚度小于0.04d时,侵彻深度随药型罩厚度的增大而增大;当药型罩厚度大于0.04d时,侵彻深度随药型罩厚度的增大而减小。当炸高为0.50d～2.00d时,侵彻深度的极大值出现在0.75d附近;当炸高为0.50d～1.00d时,侵彻深度的变化幅度不大;当炸高大于1.00d时,侵彻深度随炸高的增大而减小。随装药高度的增大,侵彻深度逐渐增大,但幅度逐渐减小。

(2) 对正交试验结果的分析表明,各因素对环形聚能装药侵彻能力的影响主次顺序为:药型罩锥角>炸高>装药高度>药型罩厚度,药型罩锥角对侵彻深度的影响非常显著,而药型罩厚度、装药高度及炸高的影响相对较小。

(3) 对药型罩锥角的进一步优选表明,当药型罩锥角为80°～100°时,侵彻深度在90°时达到极大值;当药型罩锥角为80°～90°时,侵彻深度随药型罩锥角的增加而略有增加,但增加幅度不大;当药型罩锥角大于90°后,侵彻深度随药型罩锥角明显减小。

(4)环形聚能装药的最终优化方案:药型罩锥角为90°,药型罩厚度为0.05d,装药高度为2.00d,炸高为1.25d。该方案的侵彻深度可达0.94d,与初始方案0.66d相比,提高约43%。