磁场对重介质旋流器介质稳定性的影响

杜鹏涛,赵世永,肖雨辰,杨珍妮

(西安科技大学 化学与化工学院,陕西 西安 710054)

0 引 言

重介质旋流器因结构简单,单位处理量大,分选效率高,在选煤行业应用广泛。然而重介质悬浮液是磁铁矿粉与水组成的非均相体系[1],在离心浓缩作用下,极易造成悬浮液稳定性变差,分选精度降低等实际生产问题[2-3]。重浮液稳定性与表观黏度相关,表观黏度越高,稳定性越好[4]。因此,为提高重悬浮液的稳定性,诸多学者进行了大量研究。赵卫等[5]探究了重介质粒度对悬浮液稳定性的影响,以浓缩度、澄清度、分层度以及浓缩效率作为重悬浮液稳定性的评价标准。研究发现重介质粒度越小,悬浮液稳定性越高,同时黏度也越大。当重介质粒度小于0.045 mm、含量大于90%时,悬浮液稳定性最高。段福山[4]研究表明当分选密度较低时,采用细粒级重介质;分选密度较高时,采用含煤泥的粗粒级重介质,可使悬浮液表观黏度保持正常。张志军等[6]分析了煤泥含量对重悬浮液稳定性和流变性的影响。研究发现,煤泥含量越高稳定性越好,但表观黏度的增加导致流变性变差,分选精度降低。悬浮液密度1.5 g/cm3,煤泥质量分数为20%时,悬浮液稳定性达到最佳。祁泽民等[7]认为煤泥含量代表悬浮液的黏度,兼顾悬浮液稳定性和流变性的同时,存在煤泥含量的最佳值。路永广等[8]利用表面活性剂增强重悬浮液的稳定性,研究发现非离子型表面活性剂在不影响重悬浮液双电层的同时增加了空间位阻效应[9],提高了重悬浮液表观黏度和稳定性。

采用细粒级重介质颗粒,可提高重悬浮液的稳定性,但同时表观黏度的提高降低了重悬浮液的流变性,增加错配几率且工业化成本较高;表面活性剂的大规模使用会提高工业化成本且会间接影响煤炭分选系统的其他环节;适量煤泥可提高重悬浮液的稳定性,但工业生产中煤泥含量的实时控制有待解决。上述方式均通过增加悬浮液的表观黏度来提高其稳定性,但也损失了重悬浮液的流变性,二者无法同时满足。

重悬浮液并不具备保持悬浮状态的能力,需引入外加能量来降低浓缩作用的不利影响[10]。利用磁场改变重介质的分布状态,削弱重悬浮液所受浓度作用,提高其稳定性。在不改变重悬浮液表观黏度和流变性的前提下,提高重悬浮液稳定性。

1 理论基础

根据沉降末速理论,在径向浓缩的作用下,不同粒度的重介质颗粒具有不同的离心沉降末速,从而在轴向浓缩作用下,密度分布不同。

1.1 重介质颗粒在离心场中的沉降末速

在离心沉降过程中,重介质颗粒先加速后减速,在离心力Fc、压差阻力fp以及流体曳力fd达到平衡时,颗粒速度vr在离心场中达到离心沉降末速vr0。此时有

vr=vr0,Fc=fp+fd,

(1)

即

(2)

式中,d为固相颗粒直径,mm;ρs为固相颗粒密度,g/cm3;ρ为液相密度,g/cm3;ω为固相颗粒离心转速,r/s;r为固相颗粒离心旋转半径,mm;λ为流体阻力系数;S为固相颗粒的帆面面积,S=(π/4)d2,mm2;vr为固液两相间的相对速度,m/s。

不同粒度的重介质颗粒拥有不同的离心沉降末速vr0[11],粒径越大vr0越高:

(3)

1.2 重介质颗粒在磁力复合场中的沉降末速

在离心力场中,引入指向轴心的径向磁场力fm,颗粒受到离心力Fc、压差阻力fp、流体曳力fd和磁力fm,受力情况如图1所示。

图1 复合场中重介质颗粒受力分析Fig.1 Force analysis of particles in compound field

磁性颗粒所受磁力可表示为

(4)

式中,χ为比磁化系数;H为磁场强度,A/m;gradH为磁场梯度。

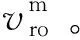
(5)

即

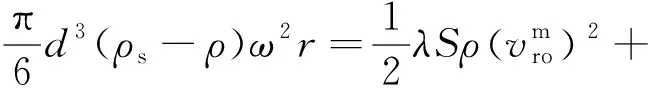
(6)

将式(3)代入式(6),则有:

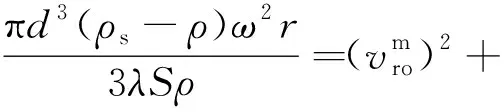
(7)

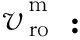
(8)

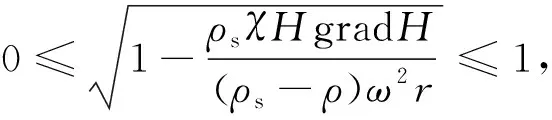
2 试 验

2.1 重介质性能检测

试验选用某选煤厂纯磁铁矿粉作为试验原料,真密度为4.29 g/cm3,磁性物质量分数为95.3%。对于选煤用磁铁矿粉,一般要求粒径小于325目(45 μm)质量分数大于85%[12],原样粒径分布见表1。原样中粒径小于325目(45 μm)的重介质颗粒,筛下累计产率为86.92%,主导粒级为<500目(29.96 μm),质量分数为68.46%。

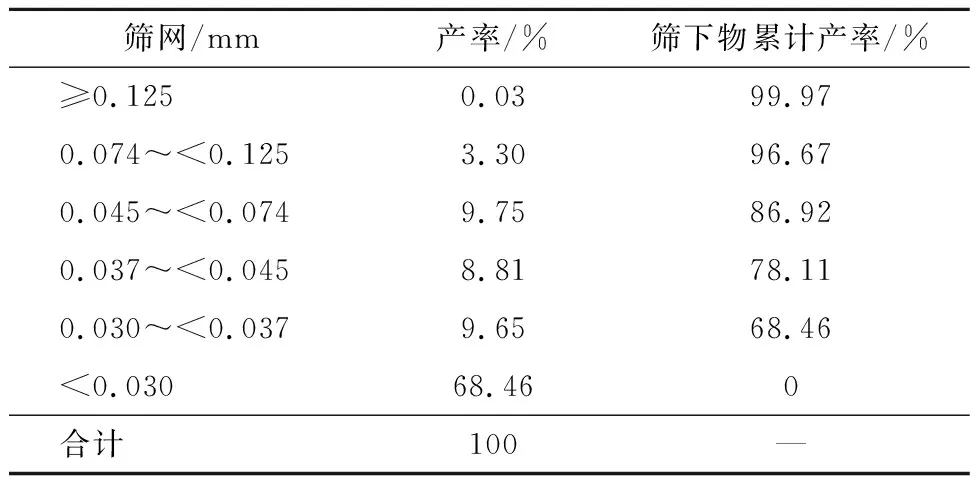
表1 磁铁矿粉粒度分析Table 1 Size analysis of magnetite powder

2.2 试验平台

试验采用自主研发的磁力调控型重介质旋流器[10],主要应用于重介质旋流器内悬浮液稳定性的在线调节,结构如图2所示,包括旋流器主体和磁力调控系统,其中磁力调控系统由内外磁极和励磁线圈组成。由导磁材料制成的内外磁极在几何结构上也是旋流器的圆柱体、上锥体和溢流管,具体参数见表2。由于内外磁极表面积存在较大差异,在励磁线圈的作用下,内磁极溢流管附近的磁场强度更大,因此形成沿径向向内逐渐增大的磁场强度,即重介质颗粒在径向上受指向轴心的磁场力。通过调整励磁电流大小和线圈匝数以改变磁场强度,对重介质旋流器内磁铁矿粉的运动规律进行磁力调控,从而提高重悬浮液的稳定性。

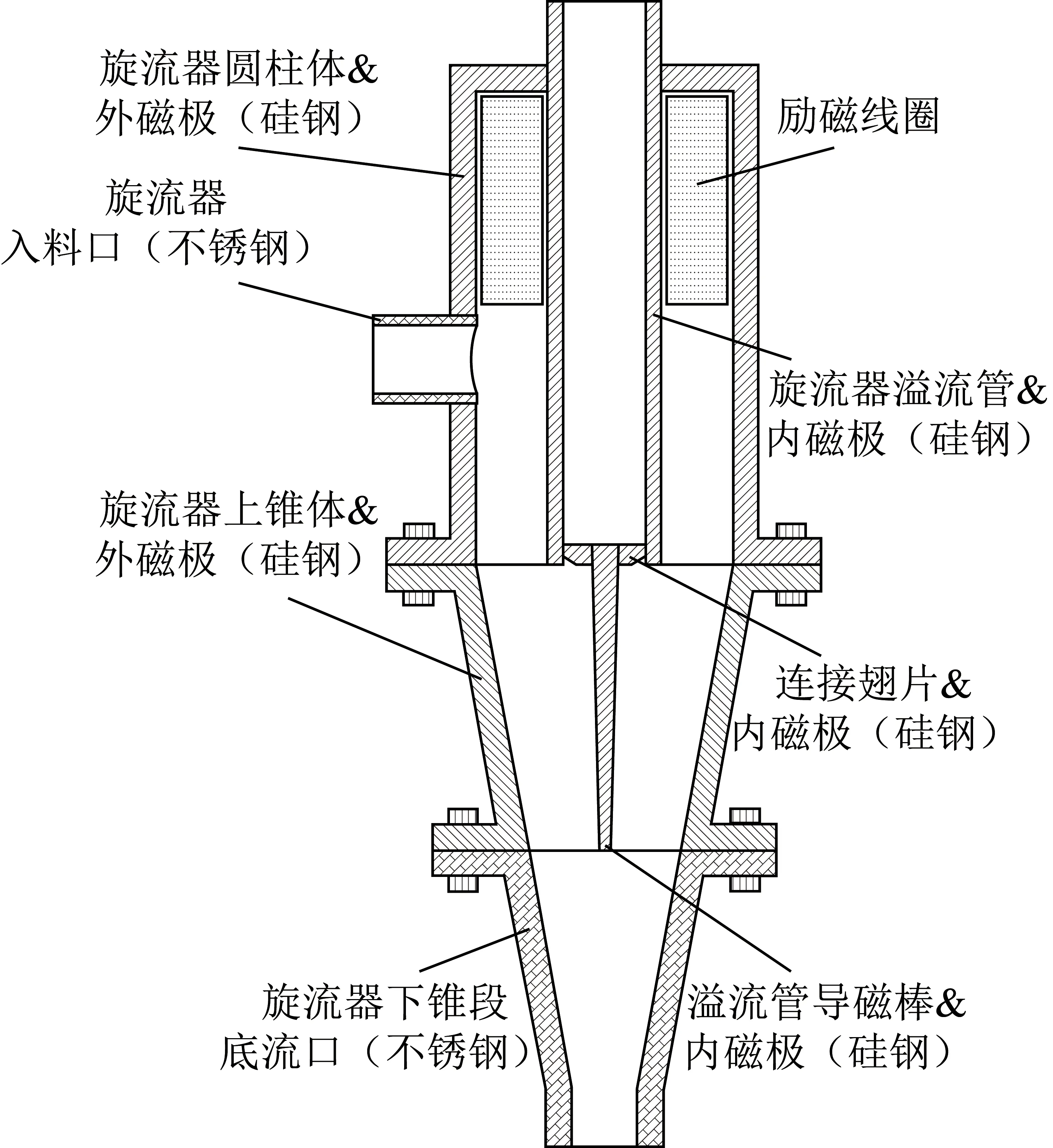
图2 磁力调控型重介质旋流器结构Fig.2 Structure of magnetic dense medium cyclone

2.3 试验内容与评价标准

在单因素试验中,为更好探究磁场对重悬浮液稳定性的影响规律,首先进行入料压力单因素试验,寻找最优试验参数,也作为磁场对重悬浮液稳定性影响的对照试验;磁场强度与电流强度、线圈匝数密切相关,如式(7)所示。进一步以线圈匝数和电流强度为试验因素进行重介质分配试验,其步骤为配置一定密度的重悬浮液,充分混合均匀,以一定入料压力由渣浆泵给入重介质旋流器,待其运行平稳后,利用密度壶同时称取溢流、底流悬浮液各1 000 mL,计算溢流、底流重悬浮液密度,同时以式(9)中的浓缩度C1、澄清度C2、分层度C3及浓缩效率Eth系统表征重悬浮液的稳定性[13]:

(9)

式中,N为励磁线圈匝数;I为励磁电流强度,A;Le为有效磁路长度,mm。

在单因素试验的基础上,确定合适因素及水平,利用Design Expert正交设计软件确定各因素与响应值浓缩效率Eth的数学模型,深入探究磁场对重介质分配和悬浮液稳定性的影响规律及内在机理。

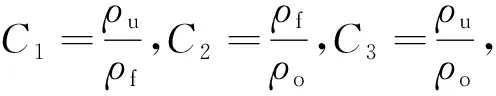
(10)

其中,ρf为入料悬浮液密度,g/cm3;ρo为溢流悬浮液密度,g/cm3;ρu为底流悬浮液密度,g/cm3;δ为重介质密度,g/cm3。若C1=C2=C3,即ρf=ρo=ρu,此时重悬浮液未发生浓缩作用,旋流器内部密度分布均匀。若C1>1时,C2、C3>1,重悬浮液发生浓缩并产生密度梯度分布[14]。

3 单因素试验

3.1 重介质分配试验

在入料压力试验中,配置密度1.4 g/cm3的重悬浮液,探究0.03、0.04、0.05和0.06 MPa入料压力对介质分配的影响规律,并确定入料压力试验参数。不同因素对溢流和底流悬浮液密度的影响如图3所示。由图3(a)可知,随入料压力增加,溢流悬浮液密度逐渐降低,底流悬浮液密度逐渐升高。说明随入料压力的增大,颗粒离心沉降末速增加,更多重介质颗粒从底流排除。入料压力的增加,可提高旋流分选效率[15],但也加剧了悬浮液所受浓缩作用,降低其稳定性[16]。因此,为兼顾悬浮液稳定性和分选效率,选取入料压力0.04 MPa为试验条件,探究磁场对重介质旋流器介质稳定性的影响规律。

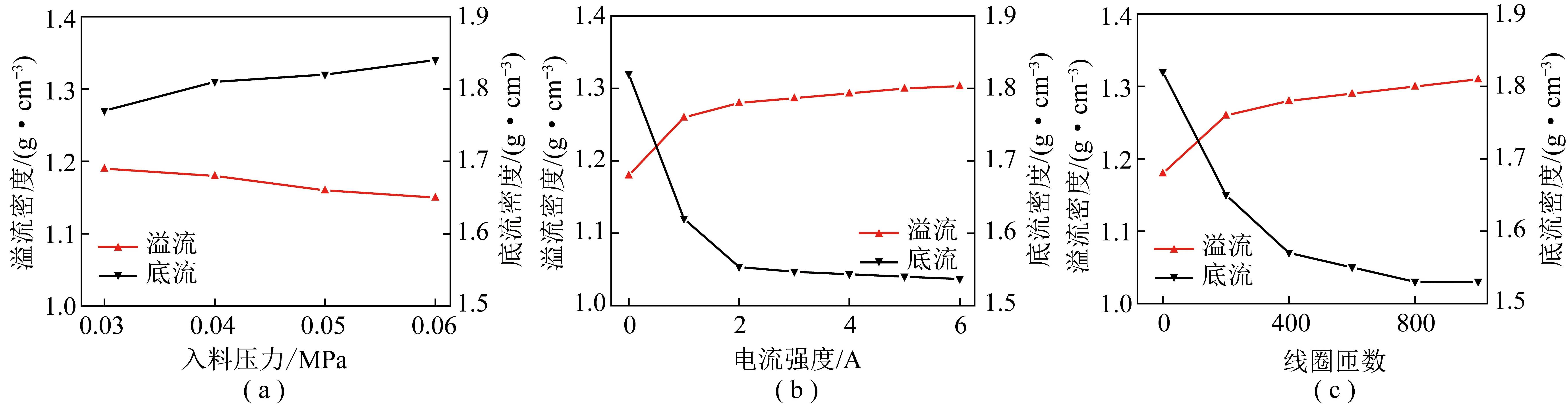
图3 不同因素对溢流和底流悬浮液密度的影响Fig.3 Influence of different factors on overflow and underflow density

在电流强度试验中,重悬浮液密度为1.4 g/cm3、入料压力0.04 MPa、线圈匝数600,探究0、1、2、3、4、5和6 A电流强度对介质分配的影响规律,并确定电流强度试验参数。由图3(b)可知,随电流强度增加,溢流密度逐渐升高,同时底流密度逐渐降低,在电流强度2 A后基本保持平稳。这说明随电流强度增加,沿径向向内的磁场力逐渐增大,颗粒离心沉降末速逐渐降低,溢流介质产率逐渐升高,底流逐渐降低。在电流强度2 A后基本保持平稳,是因为随磁场力的增加,进一步减弱了重介质颗粒的沉降末速,使其进入溢流,但不足以干扰从底流排出沉降末速较高的重介质颗粒,因此溢流、底流密度未发生明显变化。因此选取电流强度2 A进行线圈匝数单因素试验。

在线圈匝数试验中,重悬浮液密度为1.4 g/cm3,入料压力为0.04 MPa,电流强度为2 A,探究线圈匝数200、400、600、800和1 000对介质分配的影响规律,并确定线圈匝数试验参数。由图3(c)可知,随线圈匝数增加,溢流密度逐渐升高,底流密度先降低,在线圈匝数800后保持平稳。说明随线圈匝数增加,磁场强度同样增加,颗粒离心沉降末速降低,溢流介质产率逐渐升高,底流逐渐降低。线圈匝数对重介质分配的影响规律与电流强度相似,但从变化趋势上看,其略强于电流强度的影响。

3.2 各因素对悬浮液稳定性的影响规律

C1、C2及C3理论上数值越接近1,浓缩作用越小,悬浮液稳定性越高[14]。不同因素对悬浮液稳定性的影响如图4所示,由图4(a)可以看出,当入料压力在0.03～0.06 MPa时,随入料压力增加,旋流器浓缩效率Eth、悬浮液浓缩度C1、澄清度C2、分层度C3均逐渐增加。这与入料压力对重介质分配的影响规律相似。这说明随入料压力增加,颗粒离心沉降末速增大,溢流介质产率降低,底流产率升高,悬浮液所受浓缩作用增强,密度梯度分布更加显著,稳定性变差。

由图4(b)可知,随励磁电流强度增加,旋流器内部Eth、C1、C2及C3均逐渐降低。说明随电流强度增加,溢流介质产率升高,悬浮液所受浓缩作用减弱,稳定性提高,密度分布更加均匀;电流强度在0～2 A,悬浮液稳定性提高显著,随后趋于平稳。说明在2 A电流强度下的磁场力使大多数离心沉降末速较低的重介质颗粒进入溢流;而后在2～6 A,稳定性提升并不明显。对照图2(b)溢流、底流密度变化也可得到相同结论。

图4(c)与图4(b)趋势相似,随线圈匝数增加,Eth、C1、C2及C3均逐渐降低,相较图4(b)的变化趋势更加明显。说明线圈匝数对悬浮液稳定性的影响强于电流强度,线圈匝数为1 000时,悬浮液稳定性最优。

4 正交试验

磁场对Eth、C1、C2和C3的影响相似,因此取Eth作为正交试验响应值。利用Design Expert进行正交试验设计,判断因素间交互作用,寻找各因素与响应值的关系模型,进一步探究磁场对重悬浮液稳定性的影响规律。

4.1 Box-Behnken正交试验

根据单因素试验可知,入料压力为0.04 MPa、电流强度为2 A以及线圈匝数为800时,可更好探究各因素对响应值的影响,并将压力、电流、线圈匝数分别定义为因素A、B和C。正交试验水平选取见表3。

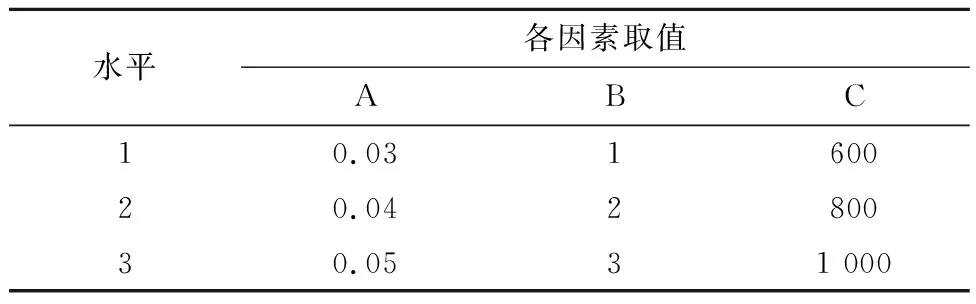
表3 正交试验因素及水平Table 3 Factors and levels of orthogonal experiment

根据Box-Behnken正交方案进行三因素三水平正交试验设计,正交结果见表4。正交试验中,如果一个因素水平选取的好坏会影响另一个因素水平的选取,则考虑2个因素间的交互作用[17]。

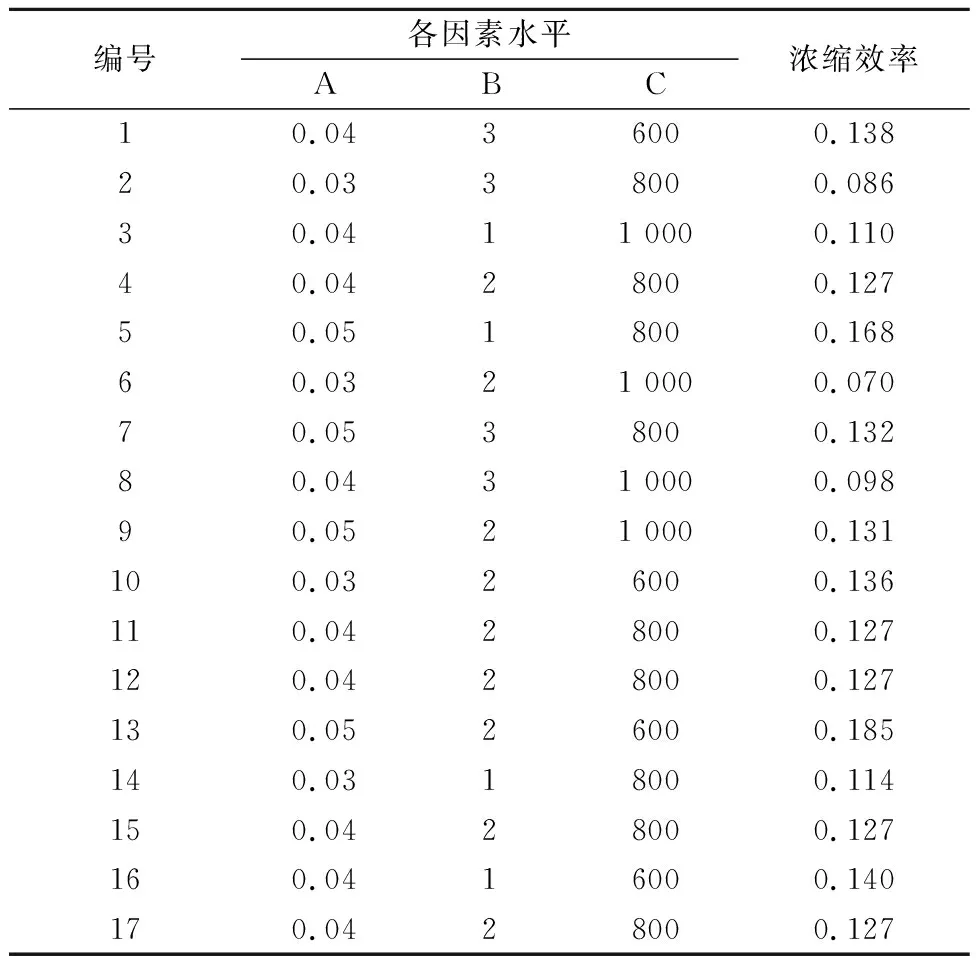
表4 正交试验方案及结果Table 4 Results of orthogonal experiment

对比2、5和7、14两组数据发现,无论因素A为0.03 MPa还是0.05 MPa,因素B水平的变化对响应值Eth无影响。因素B水平的选取与因素A对响应值的影响也无关,即因素A B无交互作用;观察1、3和8、16两组数据以及6、9和10、13两组数据,也可以发现BC以及AC无交互作用。即因素A、B和C相互独立,对浓缩作用的影响可简单叠加并存在主效应因素。

因此进行全模型拟合以及方差分析,得到各因素对Eth的数学模型。

4.2 各因素对浓缩效率的数学模型

将正交数据进行全模型拟合分析。表5、6分别为浓缩效率和不同因素之间的全模型方差分析以及R2综合分析。

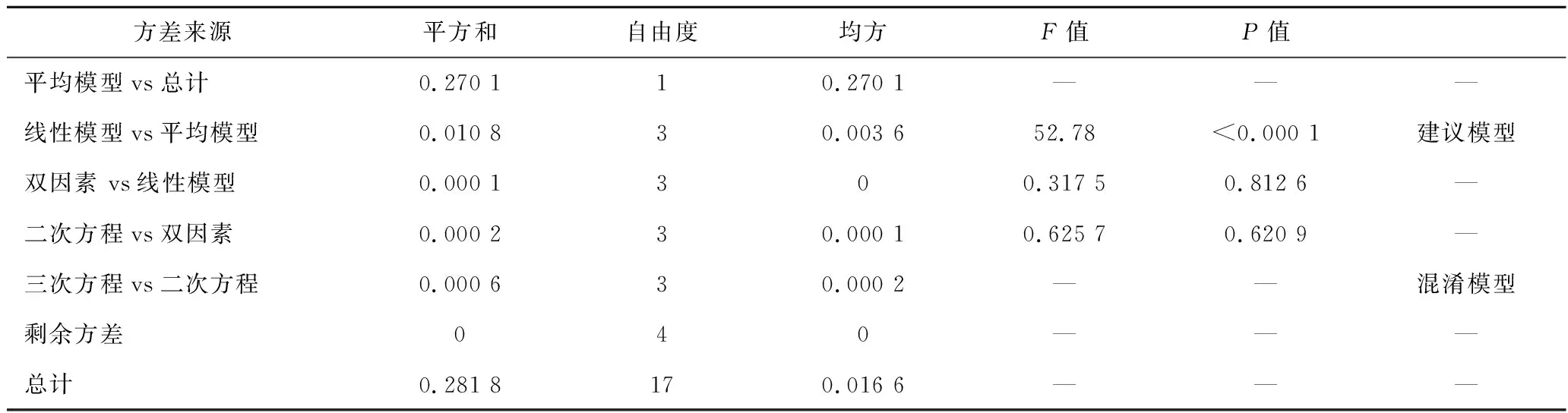
表5 全模型方差分析Table 5 Variance analysis of multiple models

表6 R2综合分析Table 6 Summary of R2 model analysis for box-behnken design

在全模型方差分析中,F越大,P越小,拟合结果越可靠[18]。在R2综合分析中,R2、R2校正值以及R2预测值越接近,拟合结果越可靠[18];R2越大,预测残差平方和越小,说明模型越合理[19]。由表5、6可知,线性模型拟合程度最高。说明入料压力、电流强度和线圈匝数与浓缩效率Eth为线性关系。

为寻找主效应因素和数学模型,进行线性模型置信度分析,结果见表7。参数估计值既表示各因素对响应值的影响程度,也为代码方程的各项系数,其绝对值越大,对响应值影响越显著[20]。

表7 浓缩效率线性方程模型置信度分析Table 7 Reliability analysis of linear equation model to concentraion efficiency

由表7可知,因素A、B和C均为高度显著影响因素,其中A为正相关因素,B和C为负相关因素,影响程度按大小排序为:A>C>B。

由表7中的参数估计值,可得到各因素与浓缩效率Eth的代码因素方程见式(11):

Eth=0.126 1+0.026 3A-0.009 7B-0.023 8C。

(11)

为了使所得方程更符合各因素的原始单位,Design Expert将其按实际比例进行缩放,得到各因素与浓缩效率Eth的实际因素方程(12):

Eth=0.135 559+2.625 00A-0.009 750B-0.000 119C。

(12)

图5为浓缩效率学生化残差分布,其表示线性模型对正交数据的拟合程度,拟合结果越可靠,残差值越小,数据点越接近直线[21]。图中17个点基本处于直线两侧,说明模型拟合结果可靠。

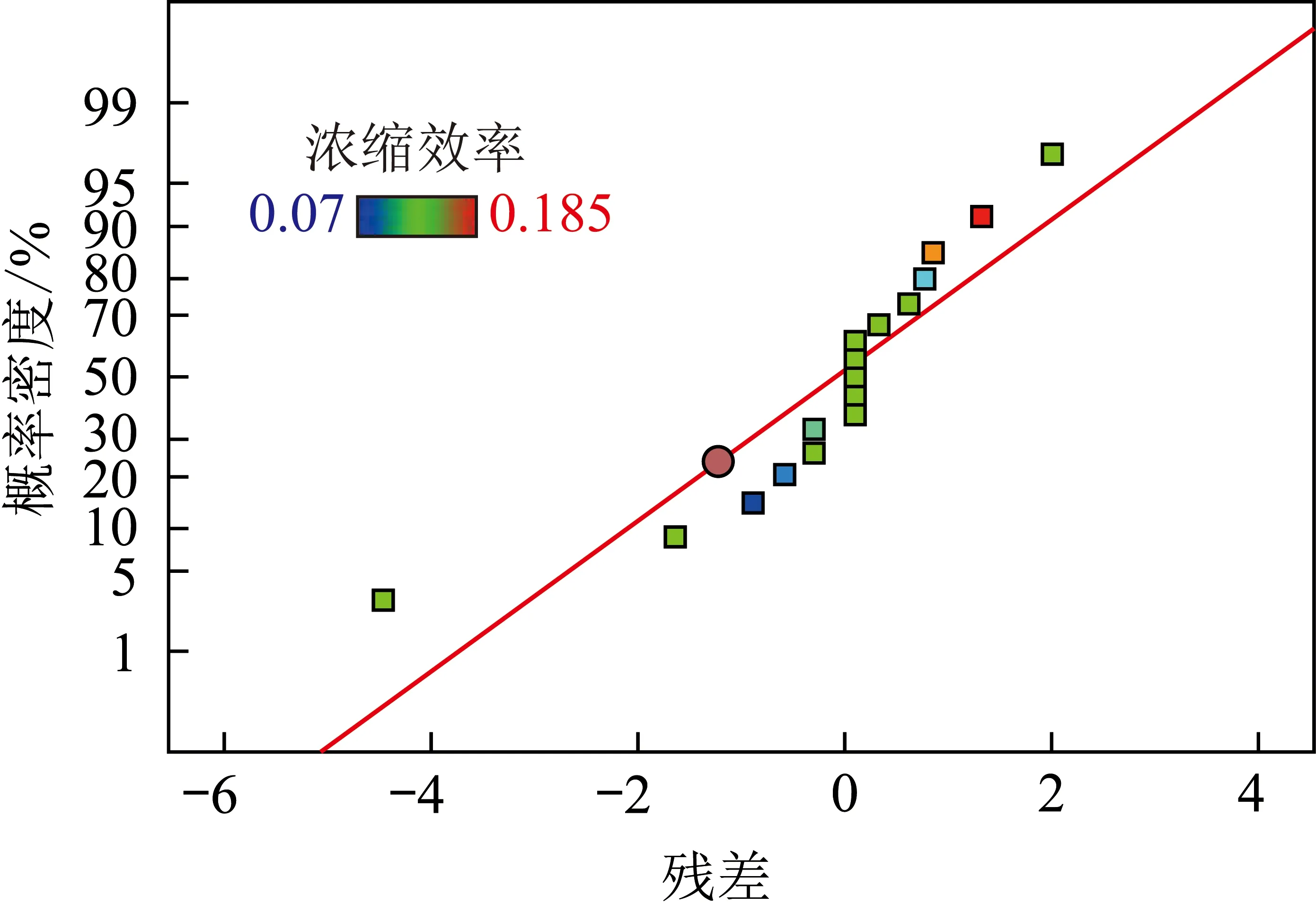
图5 浓缩效率标准差正态分布Fig.5 Normal plot of residuals to concentration efficiency

4.3 响应面优化与验证

在线性模型基础上,通过Design Expert响应面法进一步优化试验条件以寻求最优解。当浓缩效率取得极小值时,重悬浮液稳定性达到最高。试验参数的最优解见表8,并对预测值进行试验验证。

表8 浓缩效率最优方案Table 8 Optimization of concentration efficiency

将预测值取整,即当入料压力为0.03 MPa,电流强度为3 A,线圈匝数为1 000时,预测浓缩效率为0.069;将预测结果进行试验验证,实际浓缩效率为0.067,预测值与实际值误差为2.90%,未超过5.00%[22]。因此通过Design Expert得到各因素与浓缩效率Eth的线性模型结果可靠。此时浓缩效率相较于无磁场状态下的浓缩效率0.370,重悬浮液稳定性提高了81.89%。

5 结 论

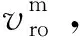
2)随入料压力的增加,重悬浮液的C1、C2、C3及Eth均呈相似增加的趋势,重悬浮液浓缩作用增强,稳定性变差;随电流强度和线圈匝数的增加,则呈现相似降低的趋势,重悬浮液浓缩作用减弱,稳定性提高。

3)浓缩效率Eth与入料压力呈正线性相关,与电流强度和线圈匝数呈负线性相关,各因素间相互独立。影响程度按大小排序为:入料压力>线圈匝数>电流强度。

4)在正交数据基础上,利用Design Expert软件拟合得到了浓缩效率Eth与各因素间的线性模型:Eth=0.135 559+2.625 00A-0.009 750B-0.000 119C。

5)利用Design Expert得到最优试验参数,即在入料压力0.03 MPa,电流强度3 A,线圈匝数1 000时,预测浓缩效率为0.069,并通过试验验证得到0.067的浓缩效率,相较无磁场状态下的浓缩效率0.370,重悬浮液稳定性提高了81.89%。在不改变表观黏度的前提下,大幅提高重悬浮液的稳定性。