应变模态振型指标下的泡沫铝夹层梁损伤识别

何欣宇,安 逸

(1.南京工业大学机械与动力工程学院,江苏 南京 211816) (2.南京工业大学数理科学学院,江苏 南京 211816)

泡沫铝为功能、结构一体化材料,具有质量轻、比刚度高、吸声隔音等特点,在轨道交通、船舶运输、航空航天等领域有着广阔的应用前景[1]。为了提高泡沫铝的力学性能,制作时常采用夹芯结构,但夹芯结构产品在生产、运输和使用时难免出现损伤,存在安全隐患,因此需要对其健康状态进行监测。传统的无损检测方法如超声检测、射线检测、红外热成像、涡流检测等,均为局部损伤诊断方法[2],且检测周期长、成本高,难以实现在线监测、全局监测和全天候监测。运用应变模态对泡沫铝夹层梁进行损伤识别研究能很好地解决这类问题。李德葆等[3]对应变模态基本理论进行了详尽论述,管德清等[4-9]从不同的角度、不同的侧面对该方法进行了讨论,做了大量的研究工作,运用应变模态结合灰色相关性理论、小波变换等方法识别了不同结构的损伤信息,并改进了模态试验技术以获取更为准确的应变模态参数。本文建立了基于修正Timoshenko梁理论的泡沫铝夹层梁的弯曲振动解析式,提出了归一化应变模态振型差指标和增强应变模态振型差指标,总结了泡沫铝夹层梁损伤引起的频率、振型的变化规律。

1 应变模态分析理论

基于位移的结构自由振动微分方程可以表述为:

(1)

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;y(t)为位移向量;t为时间。

设结构的位移、应变关系为:

y(t)=Bε(t)

(2)

式中:B为位移、应变的转换矩阵;ε(t)为应变向量。将式(2)代入式(1),方程两端同时左乘BT,整理得:

(3)

式中:Mε、Cε、Kε分别为应变模态的质量矩阵、阻尼矩阵和刚度矩阵。通过式(3)求解方程的特征值和特征向量,获得系统的固有频率及应变模态振型,记位移模态振型为φ,应变模态振型为ψ,令ε(t)=ψq,q为振型反应向量,则式(3)可以改写为:

(4)

将式(4)两端同时左乘ψT,将ψ=B-1φ代入式(4),整理得:

(5)

(6)

式中:Mr、Cr、Kr分别为主质量矩阵、主阻尼矩阵和主刚度矩阵。

可以发现,基于应变和基于位移建立的系统振动方程具有同一主质量阵、主阻尼阵以及主刚度阵,当结构出现损伤时,质量基本不变,而局部损伤部位的刚度会减小,因此结构的固有频率及振型在损伤前后会发生改变,可以通过求解结构动力学逆问题获取损伤信息。

2 泡沫铝夹层梁模态参数解析解

梁的弯曲振动理论发展先后经历了Euler梁、Rayleigh梁、剪切梁、Timoshenko梁几种梁理论,梁单元理论正在逐渐完善并接近现实情况。本文在Timoshenko梁理论的基础上进一步考虑由剪切变形引起的转动惯量对梁体振动的影响,可以得到修正的Timoshenko梁理论。参阅文献[10]建立泡沫铝夹层梁的微分振动方程。

图1 Timoshenko梁微元受力图

根据材料力学,可知剪切角表达式为:

γ=Q/(μAG)

(7)

(8)

根据梁体微元受力图列写y方向的力平衡方程以及截面形心的力矩平衡方程为:

(10)

式中:q(x,t)为梁所受的荷载函数。

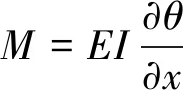
(11)

(12)

(13)

(14)

将式(13)代入式(14),整理得:

(15)

由式(15)可以发现,修正后的Timoshenko梁的微分振动方程比修正前少了一个剪切变形和转动惯量耦合项,这是由于剪切变形引起的转动惯量与该项互相抵消导致。

设n(t)=esin(ωt+η)+fcos(ωt+η),其中e、f为通解函数的待定常数,ω为圆频率,η为相位,则y=φ(x)n(t),φ(x)为模态振型。采用分离变量法求解式(15),由于模态分析是在自由振动情形下进行的,令q(x,t)=0,因此可以得到:

(17)

φ(x)=asin(αx)+bcos(αx)+csinh(βx)+dcosh(βx)

(18)

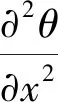
(19)

将h2、y=φ(x)n(t)以及式(18)代入式(19)可以得到梁截面的转角振型函数Θ(x):

(20)

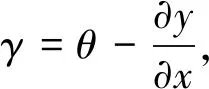
Γ(x)=(U-α)acos(αx)-(U-α)bsin(αx)+(V-β)ccosh(βx)+(V-β)dsinh(βx)

(21)

(22)

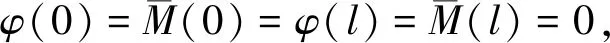
(23)

将前文中的h2、p2代入U、V,可得Uα+Vβ=α2+β2,故b=0,d=0,又因为βl为正值,则sinh(βl)只能为正值。由式(23)可以解出c=0,sin(αl)=0。故α可以表示为:

(24)

n为sin(αl)根的个数,对应梁固有频率和振型函数的阶数,通过α可以解得ωn、φn(x)和ψn(x)为:

(25)

式中:ωn、φn(x)、ψn(x)分别为第n阶固有频率、位移模态振型和应变模态振型;h1为梁高。将式(25)应用到泡沫铝夹层梁中,记泡沫铝夹层梁上、下面板的厚度为tfp,弹性模量和剪切模量分别为Efp、Gfp;芯子的厚度为tc,弹性模量和剪切模量分别为Ec、Gc。文献[11]指出,夹层梁的等效抗剪刚度(GA)eq和等效抗弯刚度(EI)eq为:

(26)

(27)

式(26)、(27)分别除以矩形梁的截面积和梁截面对中性轴的惯性矩得到泡沫铝夹层梁的等效剪切模量Geq和等效弹性模量Eeq:

(28)

(29)

将式(28)、(29)代入式(25),可以得到式(30),式(31)为夹层梁的密度公式,通过式(30)、(31)计算泡沫铝夹层梁的前4阶固有频率的解析解,结果见表1。取梁l=0.54 mm,b=0.04 mm,tfp=0.003 m,tc=0.018 m,面板材料为工业纯铝,弹性模量Efp=72 GPa,剪切模量Gfp=26.7 GPa,泊松比υfp=0.35,密度ρfp=2 700 kg/m3;芯子材料为闭孔泡沫铝,弹性模量Ec=206.4 MPa,剪切模量Gc=80 MPa,泊松比υc=0.29,密度为ρc=540 kg/m3。

表1 前四阶固有频率解析解

(30)

(31)

3 泡沫铝夹层梁损伤识别数值模拟

本文采用和闭孔泡沫铝相似的十四面体模型进行建模,但在求解时显示计算机内存不足,因此根据泡沫铝夹层梁的结构特点,做一些必要的简化。下文将夹层梁模型修改为矩形实心梁。

为探讨泡沫铝夹层梁损伤位置、损伤程度、损伤数量和模态参数之间的规律,仿真将梁离散为100个单元,在夹层梁芯子的第35、65单元设置损伤,各工况参数见表2。

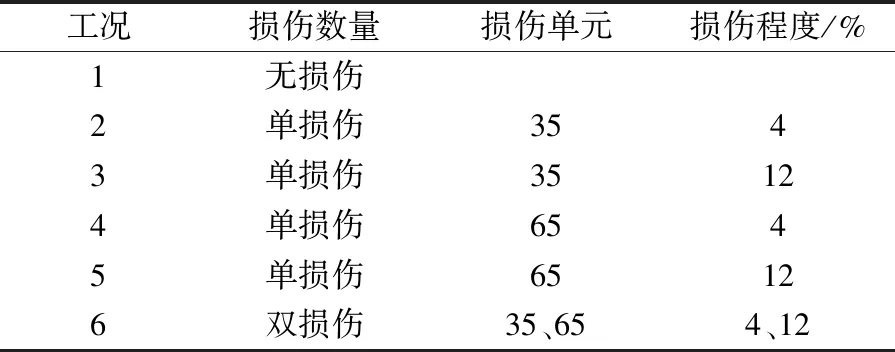
表2 模型损伤工况

采用折减单元抗弯刚度的方法模拟损伤,以两端简支边界条件为例,提取各工况的前4阶固有频率,见表3。

表3 各工况前4阶固有频率数值解

表3中δ1为健康梁固有频率解析解和数值解的误差。从前四阶固有频率的误差可见,本次仿真的结果是有效的。误差主要来源于夹层梁等效弹性模量、等效剪切模量的理论模型,以及软件中Timoshenko梁理论和文中修正Timoshenko梁理论之间相差了一个剪切变形和转动惯量耦合项,故解析解偏小,且误差随着模态阶数的增加而增加。δ2到δ6分别为工况2到工况6与健康梁固有频率的相对变化率。可以发现,总体来讲阶数越高频率的相对变化率越大,但第4阶固有频率变化率比前3阶都要小,所以有联合多阶频率识别损伤信息的必要。损伤量越大,通常频率的变化率也越大,但频率对泡沫铝夹层梁的微损伤不怎么敏感,因此固有频率变化率仅能识别泡沫铝夹层梁的普通损伤,而识别微损伤及其损伤位置则需要借助振型。

ANSYS Workbench在获取某一单元的振型值时需要定义路径导出数据,在实际测试中,应变片通常粘贴于梁的上表面,因此将路径定义于泡沫铝夹层梁上表面纵向对称轴的位置。通过导出的振型数据绘制点线图,位移模态振型如图2所示。

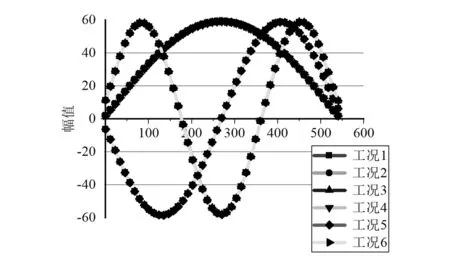
图2 各工况前3阶位移模态

泡沫铝夹层梁的位移模态振型幅值为59.168,由于损伤数值太小,因此被幅值淹没了。可见,位移模态振型对微损伤也不敏感。为了放大损伤信息,提取了泡沫铝夹层梁的应变模态振型,如图3所示。图3中应变模态振型的幅值为5.055 7E-03,可以发现,应变模态振型对损伤识别的敏感度较位移模态振型要好,但同样不够显著。下文通过损伤梁和健康梁的应变模态振型相减来放大损伤信息,提高识别效率。

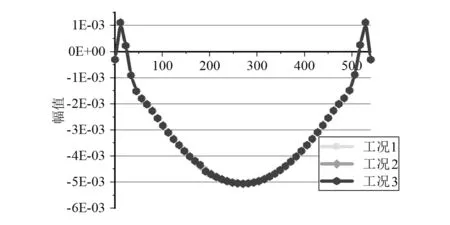
图3 第35单元损伤后的第1阶应变模态曲线

应变模态振型差分为单损伤和双损伤两类情形,如图4、图5所示。从图中可以发现,健康单元受到损伤单元的影响,应变模态振型差出现了明显的波动,而且随模态阶次和损伤程度的增加,影响也随之增加。从单损伤工况的第1阶应变模态振型可以发现,工况2中损伤量为4%的第35单元的应变模态振型差为1.73E-05,工况3中损伤量为12%的第35单元的应变模态振型差为5.45E-05,约是损伤量为4%的第35单元的应变模态振型差的3倍。另外,工况4中损伤量为4%的第65单元的应变模态振型差为1.76E-05,工况5中损伤量为12%的第65单元的应变模态差为5.52E-05,可以看出,第65单元的损伤识别敏感度要优于第35单元。从双损伤的前3阶应变模态振型差可以发现,单损伤数据叠加之后即为双损伤的应变模态振型差,其中,损伤量为12%的第65单元相邻的几个单元的应变模态振型差是不容忽视的,这些健康单元的振型差相比损伤量为4%的第35单元的振型差还大,影响了损伤识别的精度。

图4 单损伤工况的前3阶应变模态差曲线

图5 双损伤工况的前3阶应变模态差曲线

在某些情况下,有些阶数的模态数据对损伤并不敏感,为了综合多阶模态数据进行损伤识别,提出归一化应变模态振型差指标,记为ΨNΔ(i)(图6)。为了更加直观地反映损伤位置信息,在损伤数据中引入阈值,建立增强应变模态振型差指标,记为ΨENΔ(i)(图7)。ΨNΔ(i)、ΨENΔ(i)可以表示为:

图6 双损伤工况归一化应变模态指标

图7 双损伤工况增强应变模态指标

ΨENΔ(i)=u(ΨNΔ(i)-ξ)

(32)

式中:(i)、Ψdn(i)分别表示泡沫铝夹层梁第n阶的第i个损伤单元和未损伤单元的应变模态振型;u(x)为单位阶跃函数;ξ为损伤阈值。本文n取3,ξ取35%。

从图6可以发现,梁的189 mm和351 mm邻近区域分别对应第35单元和第65单元,第35单元归一化应变模态振型差对微损伤的识别效果良好,指标值为37.25%,约为第65单元归一化应变模态振型差的三分之一。从图7可以看出,增强应变模态差指标,在第65单元附近判定的损伤单元较多。通常情况下,损伤就在这些相邻单元的中间位置,通过引入阈值可以将因损伤导致梁的健康单元中产生的错误信息剔除,便于计算机程序识别。

4 结束语

采用修正Timoshenko梁理论计算泡沫铝夹层梁固有频率,与有限元数值解基本吻合,验证了夹层梁等效弹性模量、等效剪切模量理论应用到泡沫铝夹层梁的可行性,本文中的弯曲振动理论除了可应用于泡沫铝夹层梁,还可以推广至其他夹层梁当中。固有频率和位移模态振型对泡沫铝夹层梁的微损伤识别不够敏感。通常,泡沫铝夹层梁损伤单元的应变模态振型差会随着损伤量以及模态阶数的增加而增加,但某些阶数的模态对损伤并不敏感。归一化应变模态振型差指标能够综合多阶模态信息,有利于损伤识别,增强应变模态指标具有一定的抗噪功能,对实验模态分析和运行模态分析能起到一定的指导作用。两项指标为泡沫铝夹层结构在线监测、全天候监测扩充了理论依据,并提高了损伤识别的效率和精度。