文本约束下基于表示学习的知识图谱补全研究

曹 越

（西南交通大学制造业产业链协同与信息化支撑技术四川省重点实验室，成都 611756）

0 引言

知识图谱是现今非常热门的一个研究领域，现已存在以Freebase［1］、WordNet［2］为代表的几大知识图谱，它们都包含了大量表示事实的三元组，这些三元组通常的形式为头实体、关系和尾实体。但是知识图谱常是不完全的，从而有了对知识图谱补全技术的研究以完善图谱。

知识图谱补全也可称图谱中实体的链路预测，链接预测就是根据已观测到的节点和链接，来判断某个链接出现的可能性有多大。链接预测是将复杂网络与信息科学联系起来的重大纽带，主要处理信息科学中的基本问题——确定信息的还原和预测［3］。知识图谱补全可以分作基于规则和基于表示学习的两类［4］，本文的研究工作围绕隐式关联信息挖掘能力较强的知识表示学习进行。

现今TransE 等［5-14］许多经典基于表示学习的知识图谱补全模型主要围绕图谱三元组结构、网络结构特征的提取工作构建，这使得知识图谱本身的文本信息缺乏有效利用，也存在利用文本信息的补全模型如KG-BERT［15］，但其计算成本高并且不能充分提取图谱的结构特征。但是很多时候实体的文本信息不免会对相邻实体的向量表示产生影响，因此本文尝试结合两部分特征，以聚合相邻实体关系特征作为自身实体特征表示的图卷积神经网络为基础，尝试使用预训练语言模型获取邻域实体文本描述信息的文本向量表示，以供加权约束来影响实体关系的知识表示。

1 相关工作

知识表示学习，也被称为知识图谱嵌入，旨在学习知识图谱中实体和关系的分布式嵌入，即将实体和关系通过一定约束映射为低维向量，现有的知识表示学习方法主要可以分为三类，一类是以TransE［5］为代表的平移思想模型，TransE 通过向量平移将实体和关系映射到同一个向量空间；后续提出的TransH［6］、TransR［7］等衍生模型通过不同方法将关系做出区分来处理TransE 无法有效处理一对多、多对一和多对多关系的问题并进一步提升了模型性能。一类是以RESCAL［8］、DistMult［9］、ComplEx［10］为代表的模型，核心思想是用一个关系矩阵表示两个实体间潜在关系的交互作用。最后是结合深度学习的表示学习模型，ConvE［11］结合卷积神经网络，先连接一对头实体和关系的重塑向量表示，然后用二维卷积来预测尾部实体；InteractE［12］在ConvE 的基础上增加了特征交互；R-GCN［13］、CompGCN［14］则是引入了图神经网络将相邻的实体和关系一起进行编码后使用特定解码器进行评分。另外也有部分学者做了结合文本表示的相关模型研究，如NTN［16］提出使用外部语料库学习词向量并将实体表示为其包含词向量的平均值；KG-BERT［15］将图谱中的三元组看作文本序列，将三元组中实体和关系的名称或描述作为输入微调BERT［17］计算三元组分数。

2 实体文本表示约束的图卷积知识图谱补全模型

本文以图卷积神经网络为基础，参考Comp-GCN［14］模型并在其基础上使用BERT预训练语言模型获取实体文本描述信息的向量表示，用于计算关联度以作为文本加权约束来影响实体关系向量表示的学习。

2.1 相关定义

本文定义知识图谱为G=(E,R)，E、R分别代表知识图谱中实体和关系的集合，e∈E和r∈R分别代表实体集合中的实体和关系集合中的关系，定义三元组为(eh,r,et) ∈G，其中eh、et∈E分别表示头尾实体，r∈R表示头尾实体间的关系。知识表示学习就是基于现存三元组学习知识图谱G中实体e∈E和r∈R的向量表示e∈Rd和r∈Rd，其中R 表示实数集，d是向量表示的维度。表示学习的下游任务是链路预测，本文给定头实体e∈E和关系r∈R的向量表示e∈Rd和r∈Rd，预测尾实体e'∈E，即预测(e,r,e') ∈G是否存在。

然后定义任意实体e∈E经输入BERT 模型后得到的实体文本描述向量表示为te∈Rh，h是BERT 模型输出文本向量的维度。同时，与CompGCN 的工作一样，需要对数据集的所有关系做一个反向关系和所有实体自环关系的补充［14］，即对每一条存在的三元组(e,r,e') ∈G都补充一条逆向三元组(e',rinv,e) 于G中使得(e',rinv,e) ∈G（其中rinv为r∈R的逆关系）；以及对每一个存在的实体e∈E都补充一条自环三元组(e,rself,e)于G中使得(e,rself,e) ∈G（其中rself为e∈E的自环关系），即按如下公式更新G为

由此存在关系集合R的逆关系集合Rinverse=以及实体集合E的自环关系集合Rself=。将R赋值于Rori，即Rori=R，然后同时按如下公式更新R为

最后，在该模型中需要聚合与任意实体e∈E直接相连的所有实体和关系集合中（在这里称为邻域实体和其对应邻域关系）的特征作为实体e的向量表示，因此本文定义N(e)为实体e的邻域三元组集合，Nent(e)为实体e的邻域实体集合，Nrel(e)为实体e的邻域关系集合。

2.2 模型框架

本文采用R-GCN中提到的编码器-解码器模型框架［13］。编码器在CompGCN 的基础上结合文本权值约束构建，解码器采用ConvE 模型，将三元组信息包含的任意实体e∈E和关系r∈R的初始向量eini∈Rd和rini∈Rd输入到编码器进行文本加权约束下的图卷积聚合操作一次后得到对应的eaggr∈Rd'和raggr∈Rd'，再通过解码器即链路预测打分函数的约束来评价，这是模型的前向过程，然后反向更新eini和rini等其他相关参数，并反复进行该过程以实现模型的训练，模型训练完成后得到的eini和rini就是实体e∈E和关系r∈R的最终向量表示。框架结构如图1所示。

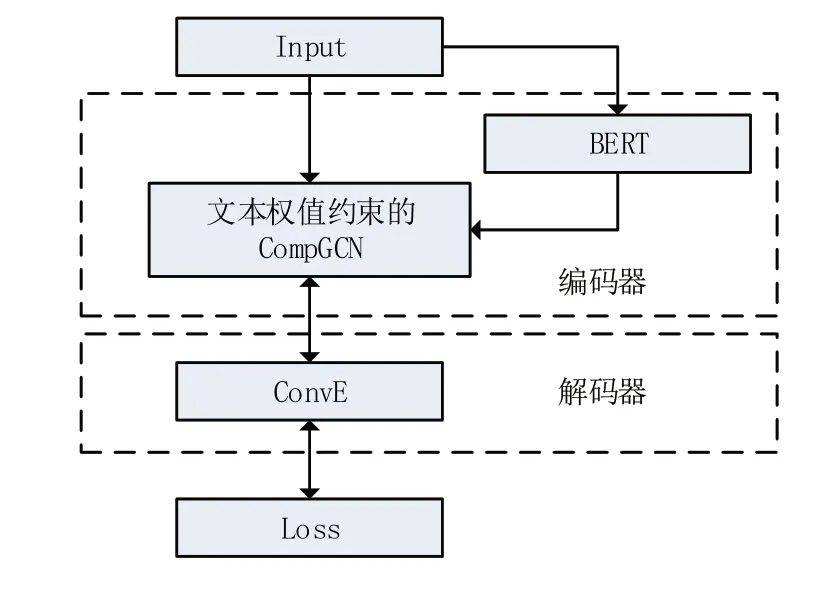
图1 模型框架

2.3 编码器

本文采用CompGCN 模型作为编码器的基础，并且考虑在图谱中常有一种情况：对于一个示例实体eexp∈E， 其邻域实体集合为Nent(eexp)， 对于集合中一个邻域实体ei∈Nent(eexp)，若它与Nent(eexp)中其余的实体的关联度较小，则它的特征信息于该集合中相对独特，对实体e的影响相对较大，相反若它与其余实体的关联度较大，其特征信息相对普通，对实体e的影响相对较小。

因此本文约定对于实体eexp∈E，任一邻域实体ei∈Nent(eexp)，其与邻域实体集合中其余实体的关联度由αi来衡量：

其中cos 表示余弦相似度，式（3）中∑表示的是αi需要累加ei和eexp的所有邻域三元组中相邻实体ej（考虑重复）的余弦相似度绝对值，同时因为eexp和ej无法确定唯一的三元组，即无法确定唯一的关系r，因而此处写作rk，rk∈Nrel(eexp)。并如前述可得，ei对eexp的影响系数可表示为

由式（3）、（4）可知，对于实体ei∈Nent(eexp)，它与Nent(eexp)中其余实体的关联度越小，其对实体eexp的影响系数越大；相反关联度越大，影响系数越小。

并于此设置可训练参数γ使得聚合权值pi可表示为

而后对所有实体进行其邻域实体和关系特征的聚合操作，聚合示意图如图2、图3 所示，图中以聚合实体e1、e2、e3、e4的初始向量得到e3的聚合表示为例。

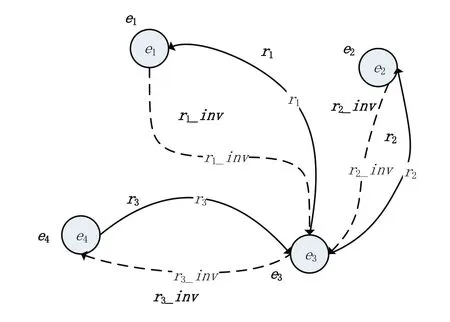
图2 关系结构

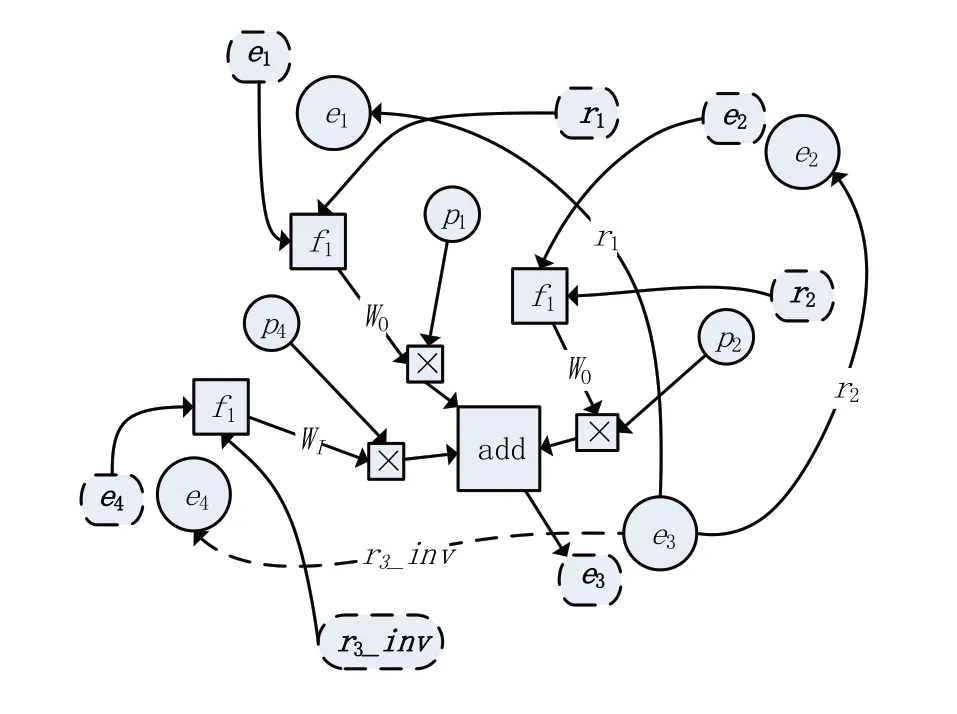
图3 聚合方式

本节后续公式均基于CompGCN 模型［14］展开，围绕上述示例实体eexp来阐述聚合过程，eexp的具体聚合公式为

其中，m表示向量的第m列。

其中Wtype(r)∈Rd'×d根据2.1 节相关定义分为三个可训练参数，公式为

聚合得到实体eexp的向量表示后，通过可训练参数矩阵Wrel∈Rd'×d获取每一个对应相邻关系rt的向量表示：

2.4 解码器

本文采用使用二维卷积的ConvE 模型［11］作为解码器，基于2.3 节每次模型前向聚合得到的实体和关系的向量表示和打分函数进行链路预测，并通过优化链路预测的效果来更新模型的可训练参数。针对任意三元构成的三元组(e,r,e')，打分函数如下：

其中：f2是ReLU 非线性映射函数用于加快模型训练；eaggr,raggr,e'aggr为通过2.3节编码器学习到的相应向量表示；,是eaggr,raggr的二维重塑形式；表示拼接操作；ω为卷积的过滤器；vec 代表的是对卷积层获取的特征进行的维数重塑操作；W是参数转换矩阵，最后通过W将特征映射输出与e'aggr同维并与其做内积操作获取得分。

3 实验和结果

3.1 数据集

本文实验采用两个经典公开数据集FB15k-237［19］和WN18RR［11］，数据集基本信息见表1，实体文本描述信息数据取自文献［15］。

表1 数据集信息

3.2 实验配置与环境

本文实验在远程服务器上进行，服务器搭载ubuntu18.04 系统，GPU 配置为1 张RTX3090（24 GB），CPU 配置为Intel（R）Xeon（R）Gold 6330@2.00 GHz，内存配置为160 GB，BERT 使用了Google提供的BERT-base（uncased）模型。

3.3 实验结果与分析

实验中对CompGCN 模型和本文模型分别进行了同环境下（见3.2 节）的训练与测试，另外同样作为对比模型的TransE 模型、ConvE 模型、KG-BERT 模型分别引用文献［14］、文献［11］和文献［15］中报告的结果，实验结果见表2。

表2 实验结果

由表2可以得出，相比于几个基准模型，本文引入邻域实体文本权值约束改进的CompGCN模型在FB15k-237 数据集上的评价指标MRR、Hit@3和Hit@1均取得了最优值，Hit@10仅次于CompGCN；在WN18RR 数据集上的评价指标Hit@10 和Hit@3 取得了最优值，MRR 和Hit@1仅次于CompGCN。综上，本文模型在对比基准模型时都取得了相对较好的实验表现，相比于基础模型CompGCN 也有一定程度的性能提升，这证明了该模型具有一定的有效性。

另外本文同CompGCN 模型一样设置相同阈值的早停操作来防止模型的过拟合。从表3中的早停Epoch值可以看出本文提出的模型在两个数据集上训练收敛所需时间均比CompGCN 模型少约30%，这也在一定程度上说明引入邻域实体文本权值约束可以提高模型训练的收敛速度。

表3 早停Epoch

4 结语

本文针对现存部分基于知识表示学习的知识图谱补全模型未有效利用知识图谱丰富的文本信息的问题，以及部分利用文本信息的模型对图谱结构特征的缺失问题，提出了一种融合实体文本加权约束的知识表示学习方法，即以CompGCN 模型为基础，使用预训练语言模型BERT 获取邻域实体文本描述信息的文本向量表示并用于计算实体关联度以作为文本加权约束使得图卷积的聚合过程具有偏向性，以影响实体和关系的向量表示，最后在两个公开数据集上与部分模型做的对比实验也证明了该方法的有效性。在后续的研究中会尝试加入关系的文本表示而不仅限于实体文本信息，会尝试探索更多的结合文本信息作表示学习的知识图谱补全方法、更充分地利用文本信息以提高模型的表现。