裂纹长度对泡桐木材声学振动性能的影响

万珂,周静,张艺馨,张海洋,刘镇波,陈文帅

(生物质材料科学与技术教育部重点实验室(东北林业大学),哈尔滨 150040)

某些种类的木材因具有优良的振动特性,被广泛应用于制作乐器的共鸣部件[1]。木材的声学振动特性在很大程度上影响着乐器的质量。木制乐器共鸣部件对木材质量要求较高,乐器的不同部件对木材的要求亦不相同[2]。通常,乐器共鸣部件具有比动弹性模量大、声辐射品质常数大、声阻抗小等特性[3-4],要求木材不能有开裂等缺陷。但是,木材缺陷是一种常见现象,因此乐器音板用木材的出材率相对较低。当今,许多国家面临森林资源日益减少的严重问题,适合制作乐器的木材也越来越少,而中国乐器制造业近年来飞速发展,供需矛盾日渐突出[5-6]。

利用声学振动方法可实现木材缺陷的无损检测[7-9],如振动法可在不破坏木质材料本身的前提下,采集木材2个端面之间反射的混叠声波,通过傅里叶变换以等处理方法,获取信号的固有频率及样品的弹性模量、固有振型等参数,通过这些参数反映出木材的缺陷状况(位置、大小),基于振动法对木材缺陷的研究多集中于节子、孔洞、腐朽等缺陷[10-13]。Yang等[14-15]采用振动法研究了节子、孔洞缺陷对木材动弹性模量、模态振型的影响,研究表明,缺陷材与无缺陷材的动弹性模量、模态振型不同,并可以通过模态振型确定缺陷的位置。Roohnia等[16]探讨局部不均匀性的方向与位置对弯曲振动频率的影响,在木材试件不同方向和不同位置钻孔洞,并测定钻孔前后的振动频率,发现孔洞的位置和方向不同,自由弯曲振动的特性也不同。而采用振动法对于裂纹的研究相对较少,林文树[17]研究了天然裂纹与人工裂纹对声速的影响,研究表明,裂纹会使传播速度变小,随裂纹深度的增大,传播时间延长。钟旻良等[18]分析了开裂对木材共振频率、模态振型及虚频图的影响,研究表明,可通过共振频率、模态振型、虚频图检测裂纹并判断开裂的位置。

基于振动法且采用声学振动参数作为评价指标的研究主要集中于对乐器用材的改性[19-21]以及探究乐器用材各种构造因子对振动性能产生的影响[22-23],而基于振动法并采用这一评价指标针对裂纹对木材声学振动性能影响的研究相对较少。而乐器在加工中可能产生开裂缺陷,或实际使用中其共鸣部件受到环境条件(温湿度变化等)的影响,音板木材产生变形或开裂,这些现象均较为常见。因此,十分有必要开展裂纹对木材声学性能品质影响规律的系统研究。笔者以民族乐器常用材——泡桐为研究对象,研究不同位置及不同长度的裂纹对木材声学振动性能的影响,以期为裂纹对乐器共鸣板的声学振动性能产生何种影响提供一定的理论依据,对合理利用木材资源制作乐器共鸣部件也具有一定意义。

1 材料与方法

1.1 试验材料

试验选取无开裂变形、节子、腐朽等缺陷的泡桐(Paulowniaelongata)木材,加工成规格为335 mm(纵向,L)×33 mm(径向)×11 mm(弦向,T)的试件,共20块,试件各表面均刨光,加工平整。将试件置于温度20 ℃、相对湿度65%的环境下平衡1个月,调整试件含水率至12%左右。将试件平分为2组,分别记作D组、Z组,其中D组为端部裂纹,Z组为中部裂纹,裂纹均为顺纹方向,即试件的长度方向。裂纹尺寸分别为1/8L×1T、2/8L×1T、3/8L×1T、4/8L×1T4种水平,裂纹宽度均小于0.5 mm,裂纹的具体情况如图1所示。

图1 裂纹预制示意图Fig. 1 Schematic diagram of crack prefabrication

1.2 试验方法

基于梁的横向振动理论,采用试材两端自由的边界条件,用双通道快速傅里叶变换分析仪(CF-5220Z)测定木材的声学振动性能。在试样的基频节点处(与试件端头距离为0.224L)用弹力三角架将试件水平支起,用刀片敲击试件的一端,由试件另一端的信号传感器接收振动信号,并经前置放大器、滤波器后,由快速傅里叶变换(fast Fourier transform, FFT)分析处理可得试件的振动频谱及振动频率,进而计算得到试件的比动弹性模量、声辐射品质常数、声阻抗、损耗角正切、动弹性模量与动态刚性模量之比等各项声学振动性能参数[24]。以端部裂纹D组为例,首先对无裂纹试件进行测试,然后采用美工刀片先在泡桐木材一端宽度方向的中部预制出1/8L×1T规格的顺纹方向裂纹,并测试其声学振动性能,之后在此基础上预制出2/8L×1T规格的顺纹方向裂纹,并再次测试其声学振动性能,而后按此方法在此基础上预制出3/8L×1T、4/8L×1T规格的顺纹方向裂纹,并分别测试声学振动性能。将预制裂纹的泡桐木材试件得到的声学振动参数(X′)与无裂纹状态参数(X)相比较,得到预制裂纹后各声学振动参数的变化率。

各声学振动参数变化率(c)的计算公式为:

(1)

2 结果与分析

2.1 裂纹长度对泡桐木材频谱的影响

频谱分析是将时域信号通过傅里叶变换至频域进行分析的方法,可以得出各个频率的幅值和能量分布。裂纹长度对泡桐木材振动频谱的影响如图2、3所示。

图2 端部裂纹对泡桐木材振动频谱的影响Fig. 2 Effect of end crack on vibration spectrum of Paulownia wood

从图2可以看出,端部裂纹对泡桐一阶频率无影响,但随着裂纹的出现,高频部分会出现双峰,且裂纹长度越大,对高频部分影响越大。从图3可以看出,中部裂纹对泡桐的一阶频率无影响,随着裂纹长度的增加,频谱也基本不出现双峰。这是由于木材的裂纹间隙比低频部分的波长小很多,声波能够绕过裂纹,而高频部分裂纹的尺寸与高阶模式的波长接近,因此振动信号传递过程易产生反射、衍射和干涉现象,同时缺陷的边界会激发其他高频成分,影响其频谱特性。而端部裂纹对泡桐木材振动频谱的影响大于中部裂纹,这可能是因为中部裂纹受到的挤压力要大于端部,使得裂纹两侧相互贴合得更紧密。

图3 中部裂纹对泡桐木材振动频谱的影响Fig. 3 The effect of middle crack on the vibration spectrum of Paulownia wood

2.2 裂纹长度对泡桐木材声学振动参数的影响

2.2.1 裂纹长度对比动弹性模量的影响

比动弹性模量(E/ρ)是表征木材声振动性能的重要指标,代表顺纹方向细胞壁的平均动弹性模量,其中动弹性模量(E)采用横向振动法测得,其计算方法见公式(2)。E/ρ值越大,表示木材的声学性能越好[23,25]。裂纹长度对泡桐木材的比动弹性模量E/ρ及其变化率的影响如图4所示。

E=48π2ρL4f2/(m4T2)

(2)

式中:ρ为试件密度,kg/m3;L为试件长度,m;f为试件横向振动的频率,Hz;T为试件厚度,m;m为振动阶数所决定的系数。

从图4a、b中可以看出,端部裂纹长度与二至五阶的E/ρ、E/ρ变化率呈显著的线性负相关,相关系数均在-0.723以下,但与一阶的E/ρ、E/ρ变化率的相关性较弱;其中四阶、五阶E/ρ降低的幅度随端部裂纹长度增大而增大的程度相较于一至三阶明显,当端部裂纹长度为1/8L时,一阶E/ρ几乎不产生变化;端部裂纹长度为4/8L时,四阶E/ρ变化率最大,但也仅有-3.0%。从图4c、d中可以看出,中部裂纹长度与一至四阶的E/ρ、E/ρ变化率呈显著的线性负相关,相关系数均在-0.749以下,但与五阶的E/ρ、E/ρ变化率的相关性较弱;其中一阶至三阶E/ρ降低的幅度随中部裂纹长度增大而增大的程度相较于四、五阶明显,且裂纹长度为1/8L时,二阶E/ρ几乎不产生变化;当中部裂纹长度为3/8L、4/8L时,一阶E/ρ变化率最大,但也仅为-1.3%。对比图4b、d可知,一阶、三阶E/ρ降低的幅度随裂纹长度增大而增大的程度中部裂纹比端部裂纹明显,而四、五阶次的规律正好相反。总体来说,随着端部和中部裂纹长度增大,各阶E/ρ呈减小的变化趋势。这可能因为随着裂纹长度的增大,声速减小,木材的共振频率减小,导致木材的动态弹性模量(E)减小,所以E/ρ随裂纹长度增大而减小。而且随着端部裂纹长度的增大,高阶E/ρ变化率大于低阶E/ρ变化率,这可能是因为裂纹长度越大,高频部分衍射和干涉现象严重。而随中部裂纹增大,高阶E/ρ变化率不一定大于低阶E/ρ变化率,且端部裂纹E/ρ变化率高于中部裂纹E/ρ变化率,这可能是因为中部裂纹受到的挤压力大于端部。

2.2.2 裂纹长度对声辐射品质常数的影响

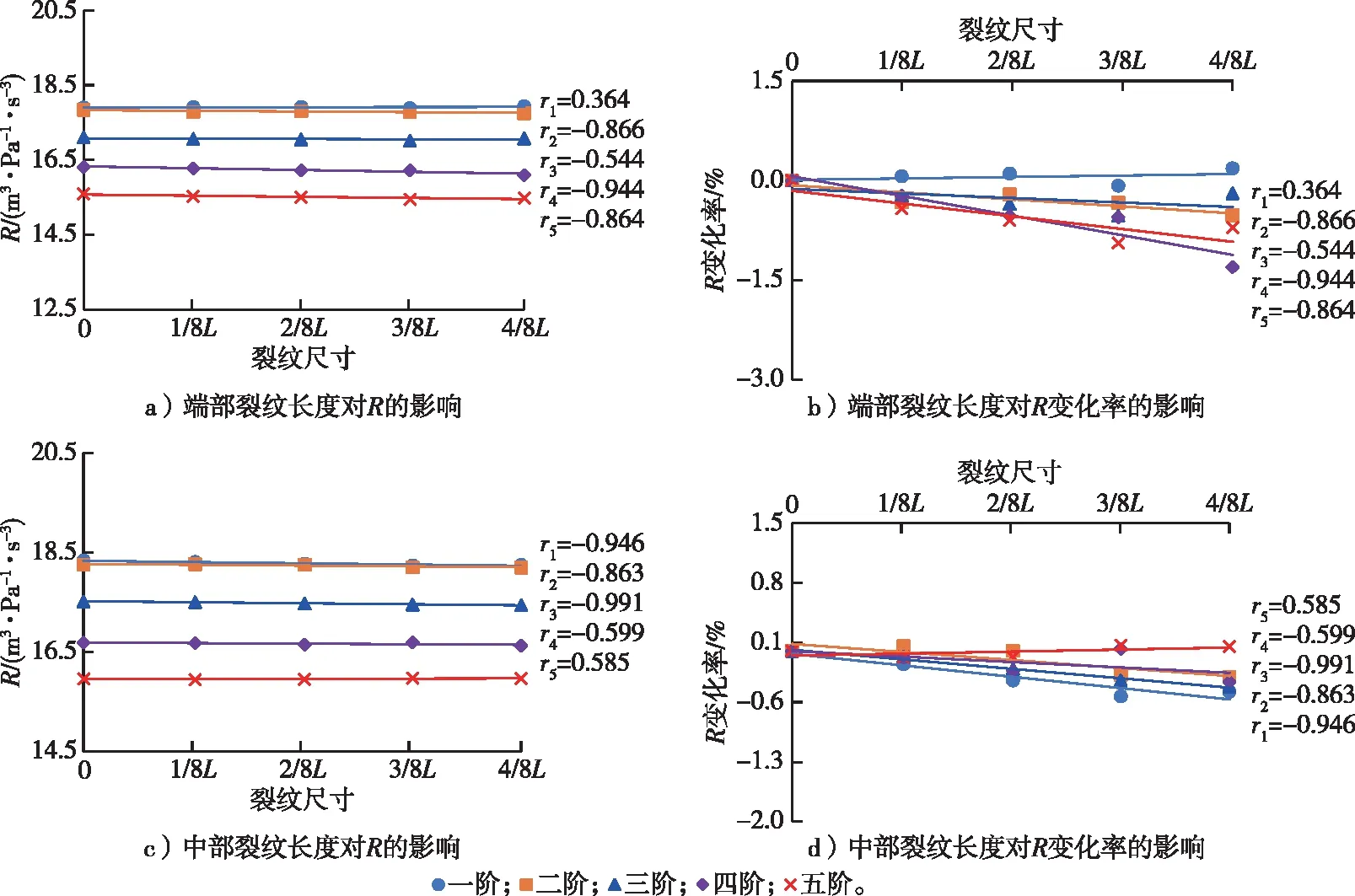
图5 不同位置裂纹长度对R及其变化率的影响Fig. 5 Effect of crack length at different positions on R and its change rate

从图5a、b可以看出,端部裂纹长度与二至五阶的R、R变化率具有明显的线性负相关,相关系数均在-0.544以下,但与一阶的R、R变化率的相关性较弱;其中四阶、五阶R降低的幅度随端部裂纹长度增大而增大的程度相较于二、三阶明显,当端部裂纹长度为1/8L时,一阶R变化率最小,仅为0.1%;端部裂纹长度为4/8L时,四阶R变化率最大,但也仅有-1.3%。从图5c、d中可以看出,中部裂纹长度与一至四阶的R、R变化率具有明显的线性负相关,但与五阶的R、R变化率具有明显的线性正相关,相关系数的绝对值均在0.58以上;其中一阶至三阶R降低的幅度随中部裂纹长度增大而增大的程度相较于四阶明显,裂纹长度为2/8L时,二阶R几乎不产生变化;当中部裂纹长度为3/8L时,一阶R变化率最大,但也仅为-0.5%。对比图5b、d可知,一阶、三阶R变化率随裂纹长度变化的程度中部裂纹比端部裂纹明显,而四、五阶次的规律正好相反。总体来说,随着端部和中部裂纹长度增大,除端部裂纹一阶R、中部裂纹五阶R外,各阶R呈减小的变化趋势,这可能是因为随着裂纹长度的增大,声速减小,导致R随裂纹长度增大而减小。随着端部裂纹长度的增大,高阶R变化率大于低阶R变化率,这可能是因为裂纹长度越大,高频部分声波衍射现象越严重。而随中部裂纹增大,高阶R变化率不一定大于低阶R变化率,但端部裂纹R变化率高于中部裂纹R变化率,这可能是因为中部裂纹受到的挤压力要大于端部。

2.2.3 裂纹长度对声阻抗的影响

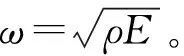
图6 不同位置裂纹长度对ω及其变化率的影响Fig. 6 Effects of crack length at different positions on ω and its change rate

从图6a、b可以看出,端部裂纹长度与一至五阶的ω、ω变化率呈显著的线性负相关,相关系数均在-0.757以下;其中四阶、五阶ω降低的幅度随端部裂纹长度增大而增大的程度相较于一至三阶明显,当端部裂纹长度为1/8L时,一阶ω变化率最小,仅为-0.1%;端部裂纹长度为4/8L时,四阶ω变化率最大,但也仅有-1.7%。从图6c、d中可以看出,中部裂纹长度与一至五阶的ω、ω变化率呈显著的线性负相关,相关系数均在-0.760以下;其中一阶至三阶ω降低的幅度随中部裂纹长度增大而增大的程度相较于四、五阶明显,且裂纹长度为1/8L时,二阶ω变化率最小,仅为-0.1%;当中部裂纹长度为4/8L时,一阶ω变化率最大,但也仅为-0.8%。对比图6b、d可知,一阶、三阶ω降低的幅度随裂纹长度增大而增大的程度中部裂纹比端部裂纹明显,而四、五阶次的规律正好相反。总体来说,随着端部和中部裂纹长度增大,各阶ω呈减小的变化趋势,这可能是因为随着裂纹长度的增大,声速减小,导致ω随裂纹长度增大而减小。而且随着端部裂纹长度的增大,高阶ω变化率大于低阶ω变化率,这可能是因为裂纹长度越大,高频部分衍射和干涉现象越严重。而随中部裂纹增大,高阶ω变化率不一定大于低阶ω变化率,且端部裂纹ω变化率高于中部裂纹ω变化率,这可能是因为中部裂纹受到的挤压力要大于端部。

2.2.4 裂纹长度对损耗角正切的影响

损耗角正切(tanδ)表征振动周期内热损耗能量与介质存储能量之比,tanδ较低的木材适合制作乐器共鸣板[28],其值为tanδ=δ/π,其中δ为对数衰减率。裂纹长度对泡桐木材的损耗角正切及变化率的影响如图7所示。

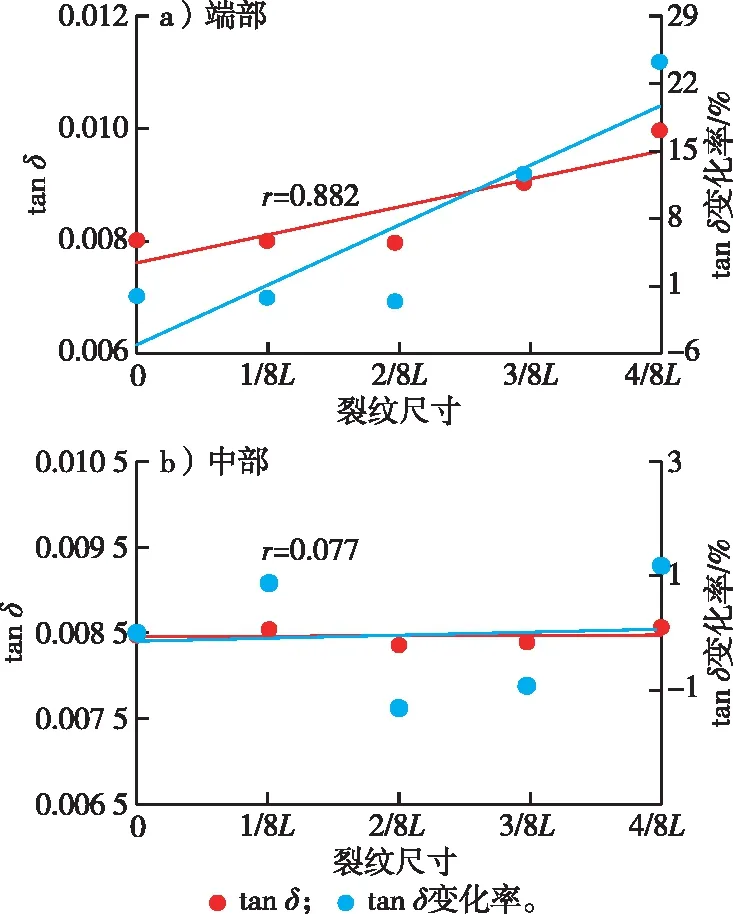
图7 不同位置裂纹长度对tan δ及其变化率的影响Fig. 7 Effects of crack length at different positions on tan δ and its change rate

从图7a可以看出,端部裂纹长度与tanδ、tanδ变化率呈显著的线性正相关,相关系数为0.882;当端部裂纹长度为1/8L时,tanδ变化率最小,仅为-0.2%;端部裂纹长度为4/8L时,tanδ变化率最大,为24.3%。从图7b可以看出,中部裂纹长度与tanδ、tanδ变化率线性相关不明显。对比图7可知,tanδ变化率随裂纹长度增大而增大的程度端部裂纹比中部裂纹明显。总体来说,随着端部裂纹长度增大,tanδ呈增大的变化趋势,这可能是因为裂纹破坏了木材原有的多胞状微观结构,改变了木材的局部密度,并且裂纹改变了木材局部的黏滞特性,所以裂纹长度越大,木材的局部密度和局部黏滞特性变化越大,tanδ变化越大。端部裂纹tanδ随裂纹长度增大而增大的程度比中部裂纹更明显,这可能是因为中部裂纹受到的挤压力要大于端部。

2.2.5 裂纹长度对E/G的影响

动弹性模量与动态刚性模量之比(E/G)可表达频谱特性曲线的“包络线”特性,能较好地评价共鸣用材振动效率和音色的综合品质。E/G值大时,说明音色效果好[22]。裂纹长度对泡桐木材的E/G及变化率的影响如图8所示。

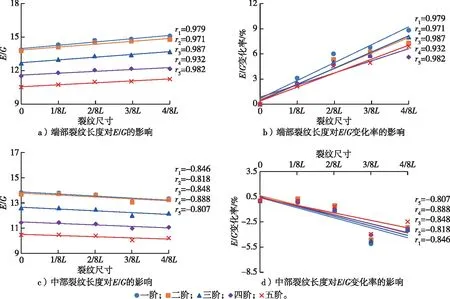
图8 不同位置裂纹长度对E/G及其变化率的影响Fig. 8 Effects of crack length at different positions on E/G and its change rate

从图8a、b可以看出,端部裂纹长度与一至五阶的E/G、E/G变化率呈显著的线性正相关,相关系数均在0.932以上;其中一至三阶E/G变化率随端部裂纹长度增大而增大的程度相较于四、五阶明显,当端部裂纹长度为1/8L时,五阶E/G变化率最小,仅为2.1%;端部裂纹长度为4/8L时,一阶E/G变化率最大,为8.8%。从图8c、d可以看出,中部裂纹长度与一至五阶的E/G、E/G变化率呈显著的线性负相关,相关系数均在-0.807以下;其中一阶至三阶E/G降低的幅度随中部裂纹长度增大而增大的程度相较于四、五阶明显,且裂纹长度为1/8L时,三阶E/G几乎不产生变化;当中部裂纹长度为3/8L时,一阶E/G变化率最大,但也仅为-5.1%。对比图8b、d可知,一至五阶E/G变化率随裂纹长度变化而变化的程度端部裂纹比中部裂纹明显。总体来说,随着端部裂纹长度增大,各阶E/G呈增大的变化趋势,这可能是因为端部裂纹使振动增强并辐射出去;而随中部裂纹长度增大,各阶E/G呈减小的变化趋势,这可能是因为声波经历了多次传播介质的变化,能量消耗变大,使振动的辐射减小。端部裂纹E/G变化率高于中部裂纹E/G变化率,这可能是因为中部裂纹受到的挤压力要大于端部。

结合“裂纹长度对频谱和声学振动参数的影响”这两部分可知,端部裂纹对泡桐一阶频率无影响,但高频部分影响较大;端部裂纹长度为1/8L时,一阶E/ρ、一阶R、一阶ω几乎不产生变化,裂纹长度为2/8L～4/8L的E/ρ、R、ω3个指标的一阶变化率均较小,且均小于对应裂纹长度四阶和五阶的变化率。中部裂纹对泡桐的一阶频率无影响,且随裂纹长度的增加,频谱也不出现双峰;中部裂纹E/ρ、R、ω变化率小于端部裂纹E/ρ、R、ω变化率。所以端部裂纹对泡桐木材振动频谱的影响大于中部裂纹,这可能是因为中部裂纹受到的挤压力要大于端部。

3 结 论

通过研究端部和中部不同长度裂纹对泡桐木材声学振动性能的影响,得出如下结论:

1)从泡桐木材振动频谱来看,端部裂纹对一阶频率无影响,但随着裂纹的出现,高频部分会出现双峰,且裂纹长度越大,对高频部分影响越大;中部裂纹对振动频谱无影响,没有出现双峰。

2)从声学振动参数来看,端部与中部裂纹对各个振动参数的影响规律有所不同,裂纹长度对振动参数的各阶次影响程度也不尽相同。总体来说,裂纹长度较大时,才会相对显著影响各项振动参数,当裂纹长度是1/8L时,各个振动参数受影响程度很小;当端部裂纹长度为4/8L时,四阶的E/ρ、R、ω,一阶的E/G以及tanδ变化率最大;当中部裂纹长度为3/8L时,一阶的E/ρ、R、E/G变化率最大,中部裂纹长度为4/8L时,一阶ω变化率最大。

3)整体来看,各声学振动参数随裂纹长度的变化而变化,但变化率较小,尤其是裂纹长度为1/8L时的一阶声学振动参数变化率最小;相较于中部裂纹,端部裂纹对泡桐木材的振动频谱影响更大,同时也会引起声学振动参数产生更大的变化,这可能是因为中部裂纹受到的挤压力要大于端部。