瞬态激励法动态测试重组竹弹性模量、剪切模量和泊松比

徐齐云,谷晓雨,王正*,陈林碧,许斌,陈清平

(1. 南京林业大学材料科学与工程学院,南京 210037;2. 福建省有竹科技有限公司,永安 366023;3. 福建鑫恒达车厢底板有限公司,三明 366035)

中国是世界最大的竹产品产出国,其竹类资源、竹林面积、竹材蓄积量、竹材的产出量以及竹产品对外贸易量均处世界各国之首。目前,竹重组材、重组竹地板、竹木复合集装箱底板等竹产品已被广泛用于市政、建筑、家具、水利、能源、交通、包装、体育、军事和休闲等领域[1]。竹材纤维强度高[2-3],但由于其结构存在中空壁薄的特性,使其在现代建筑领域的运用较少。而重组竹是以竹束为构成单元,按顺纹组坯,经热压(或冷压)胶合而成的板材,完全弥补了原生竹材的结构缺陷,极大提高了原材料利用率,彻底改变了竹材原有的性能,具有力学性能优异、物理性能变化较大等特点[4-5]。重组竹的优异力学性能同样可满足建筑用材的需求,全球近年来在该方向的研究取得了较多成果[6-8]。

弹性常数是描述材料力学性质的一个重要参数,对于建筑材料更为重要。我国现行的规范GB/T 40247—2021《重组竹》和针对结构用重组竹的LY/T 3194—2020《结构用重组竹》,均根据弹性模量值对重组竹进行了产品质量分等。目前,静力学法[9-11]是学术界用于测试重组竹弹性常数的主要方法。张俊珍等[12]用静态拉伸试验法和静态轴压试验法对慈竹重组材的弹性模量、泊松比等基本力学参数进行了测试,结果表明,该重组竹的拉伸弹性模量为32.84 GPa,压缩弹性模量为37.73 GPa,重组竹的横纹、顺纹弹性模量以及泊松比变异系数均较小,表现出良好的稳定性能。常规的静力学方法在使用时通常存在破坏重组竹试件、试验过程较为烦琐等缺陷;而动态测试法在不破坏试件的基础上,可准确地、快捷地、无损地测试出材料的弹性常数,已成为当前研究的热点方向。因此,动态测试重组竹弹性模量、剪切模量和泊松比的研究工作很有必要。

目前,重组竹弹性常数的动态测试方法主要有波速法和振动法两大类[13-15]。周先雁等[16]采用悬臂横向自由振动法对重组竹的弹性常数进行了测定,研究分析了密度以及长厚比对弹性模量的影响,研究表明,当重组竹试件的长厚比小于15时,利用振动法测算得到的弹性模量偏低,但弹性模量有着明显的随密度增大而增大的趋势。Armandei等[17]对竹悬臂梁的振动数据采用频谱分析,证明了频谱分析具有成本低、准确性高的优点。动态测试木质人造板弹性常数具有快速、简便、可靠性高等优点[18-21],已被证明是一种常用的成功方法,其测定结果与传统静态法测定结果间有较好的一致关系。此外,许多研究采用概率方法研究材料的力学性能[22-24]。当前,重组竹的动态测试研究多使用悬臂法和波速法。前者可测试弹性模量和剪切模量,多数试验仅测试了重组竹的弹性模量,未能同时测量剪切模量,且其使用的公式未考虑尺寸效应,导致长宽比、宽厚比对于弹性模量、剪切模量的测试结果具有较大影响;后者仅可测试弹性模量,且存在应变率效应,即其强度随着应变率的提高而逐渐增大[25],测试对于试件尺寸有严格要求。

根据前人研究,笔者使用自由板瞬态激励法动态测试了重组竹试件的弹性模量、剪切模量,并使用跨中贴片的悬臂板瞬态激励法[18-20]同步测试弹性模量、剪切模量和泊松比。本研究使用的测试方法考虑到尺寸效应和材料致密度的影响,试件不需要特别定制,且测得的弹性常数结果更为准确;并利用静态四点弯曲法试验验证了动态测试重组竹弹性模量、剪切模量和泊松比的准确性及可靠性。

1 材料与方法

1.1 试验材料

重组竹规格为1 860 mm(长)×1 310 mm(宽)×18 mm(厚),福建省有竹科技有限公司生产。该重组竹以毛竹为基本材料,并经锯解、碾压、干燥、浸胶和热压等工艺加工制成。

分别从同一张厚度为18 mm的整板中:按照平行竹束方向下料出756 mm(长)×126 mm(宽)×18 mm(厚)的纵向试件7根,记为AZ试件;按照垂直竹束方向下料出756 mm(长)×126 mm(宽)×18 mm(厚)的横向试件7根,记为AH试件(图1)。14根试件进行自由板瞬态激励试验和悬臂板动态试验,测量其弹性模量、剪切模量和泊松比。

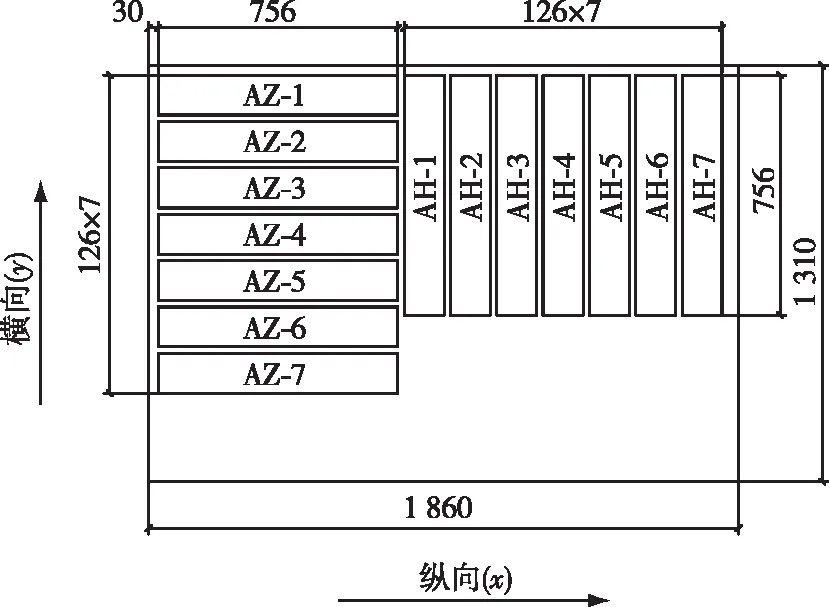
单位:mm图1 重组竹板试件下料图Fig. 1 Bamboo scrimber board cutting drawing

动态测试重组竹AZ、AH试件的弹性模量、剪切模量和泊松比后,各取1块纵向与横向板,将其锯成梁试件进行对称四点弯曲与非对称四点弯曲法静态验证试验。本次试验取AZ-6和AH-5试件,均制成380 mm(长)×18 mm(宽)×18 mm(厚)梁试件各5根,纵向编号为BZ,横向编号为BH。

1.2 测试仪器

CRAS振动及动态信号采集分析系统;CA-YD-125电压式加速传感器;JY501电子天平;游标卡尺;钢尺;HK-30感应式木材水分测试仪和橡胶锤。

1.3 弹性模量、剪切模量和泊松比动态测试

1.3.1 自由板弹性模量和剪切模量的动态测试

自由板瞬态激励法基于欧拉梁的横向弯曲理论,得到试件的弹性模量值。其自由梁的一阶弯曲频率与弹性模量E的关系为:

(1)

式中:ρ为气干密度,kg/m3;f1b为自由梁一阶弯曲频率,Hz;l为长度,m;h为厚度,m。

采用自由板扭转振型法中的自由板振型系数γ,计算重组竹自由板振型系数,得到剪切模量G。其自由板一阶扭转频率与剪切模量的关系为:

(2)

自由板振型系数γ的计算公式[26]为:

(3)

其测试原理为:在距离重组竹试件一端0.224l和0.776l处用牛皮筋进行悬挂,实现自由梁约束方式,同时在板的角点固定加速度计连接CRAS振动及动态信号采集分析系统与SsCras信号分析软件。通过锤击试件的角点激励板产生自由振动,由加速度计接收振动信号并转换为电信号输出。电信号经过调理仪放大、滤波后输入采集箱,经AD转换将模拟信号变为数字信号。经动态信号与采集分析系统软件SsCras处理得到试件频谱及其一阶弯曲和一阶扭转频率[26-27],最后经式(1)和(2)计算得到重组竹试件的E、G,如图2所示。

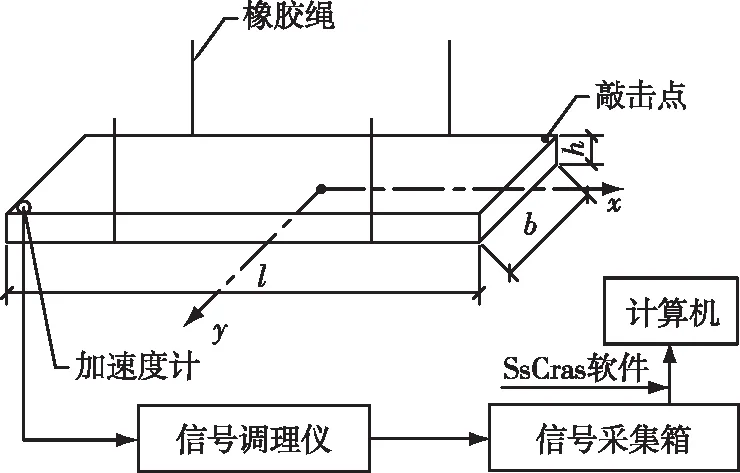
图2 重组竹自由板试件的瞬态激励测试框图Fig. 2 Block diagram of transient excitation test for bamboo scrimber free board

1.3.2 悬臂板的弹性模量、剪切模量和泊松比动态测试

基于欧拉梁的横向弯曲理论,悬臂板的一阶弯曲频率与弹性模量E的关系为:

(4)

式中,lw为悬臂外伸长度。

悬臂板一阶扭转频率与剪切模量的关系为:

(5)

式中,C1、C2为悬臂板振型系数。

悬臂板振型系数C1、C2的计算公式[27]为:

(6)

(7)

悬臂板泊松比μ为:

(8)

式中,ε90°和ε0°分别为纵向和横向应变增量。

在重组竹试件一端126 mm处用夹板夹持,实现固定约束方式(图3),形成悬臂长630 mm、宽126 mm、厚18 mm,实现其长宽比为5、宽厚比为7。在板距离固支端0.8l处安放加速度计连接CRAS振动及动态信号采集分析系统及其SsCras信号分析软件。

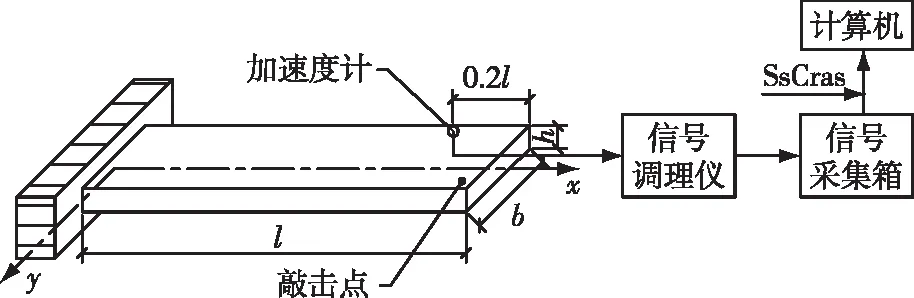
图3 重组竹悬臂板试件的瞬态激励测试框图Fig. 3 Block diagram of transient excitation test for bamboo scrimber cantilever board

其测试原理为:锤击试件角点激励板自由振动,通过加速度计接收振动信号并转换为电信号输出,再由AZ-802信号调理仪将电信号放大、滤波后输入采集箱,经AD转换将模拟信号变为数字信号,最后应用信号和系统分析软件SsCras处理得到试件频谱及其一阶弯曲频率和一阶扭转频率。

动态测试悬臂板试件的泊松比时,选择跨中贴片法,如图4所示。悬臂板上、下板面纵向应变片按半桥接法占用动态应变仪一个通道,悬臂板上、下板面横向应变片按半桥接法占用动态应变仪另一通道(2ch),即双通道测量。其应变仪的输出接信号调理仪进行放大、滤波,其滤波频率设置为频谱图上仅出现悬臂板一阶频率。

图4 悬臂试件的应变片跨中贴片图Fig. 4 Strain gauge span mid-patch diagram of a cantilever specimen

1.4 弹性模量、剪切模量和泊松比的静态验证试验

1.4.1 对称四点弯曲梁法的弹性模量和泊松比静态验证试验

对称四点弯曲梁加载示意图如图5所示。在该区段内梁的上、下表面不存在横向应力(沿梁宽度方向)等于零的点。

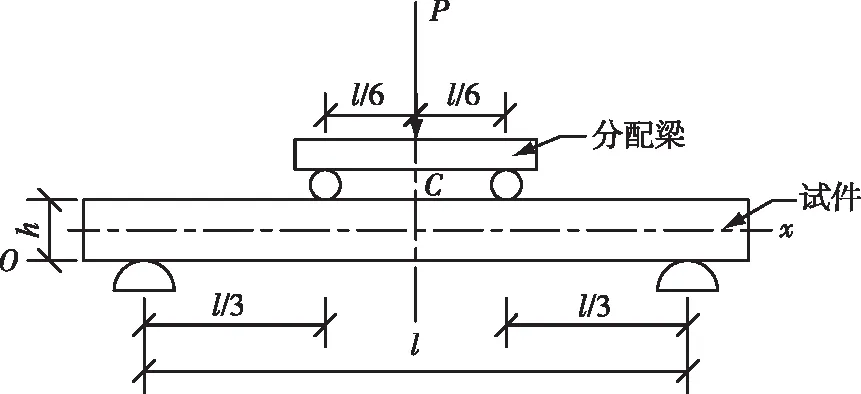
图5 对称四点弯曲梁加载示意图Fig. 5 Schematic diagram of the loading of a symmetrical four-point bending beam

对称四点弯曲梁(l/3-l/3-l/3加载)在纯弯曲段的梁上、下表面各点的正应力为:

σ=Pl/(bh2)

(9)

若梁上、下表面中心点的纵向应变为εx,则根据胡克定律,其弹性模量可表示为E=Pl/(bh2εx),写成便于测试的增量形式为:

E=ΔP·l/(bh2Δεx)

(10)

式中:ΔP为载荷增量,N;Δεx为纵向应变增量。

对称四点弯曲梁(l/3-l/3-l/3加载)在纯弯曲段的梁上、下表面中心点的横向应变和纵向应变测试值若分别为εy和εx,则泊松比可表示为:

μ=-Δεy/Δεx

(11)

式中,Δεy为横向应变增量。

在梁试件上、下表面中心点处粘贴90°(纵向)和0°(横向)应变片,对该梁施加对称四点弯曲载荷(图5),测量中心点C的纵向应变和横向应变。纵向应变和横向应变测量各占应变仪一个通道,上、下表面0°片和90°片各自采用半桥接法。

对称四点弯曲法实施2组半桥测试,将应变片分别与桥盒连接,并将桥盒接通YD-28A型动态应变仪连入AdCras信号分析系统。将试件置于支座上按图5所示位置定位,且安放辅助梁,使得加载点位于90°应变片的中心上方。分3次将1.275 kg的砝码置于辅助梁上,为四点弯曲系统施加载荷,并在每次放置砝码后利用软件记录试件应变值,进行后续计算。

1.4.2 非对称四点弯曲梁法的剪切模量静态验证试验

非对称加载四点弯曲梁试验装置示意图如图6所示。非对称四点弯曲梁法测试木材剪切模量基于剪切胡克定律和矩形截面梁中性轴上点的最大剪应力计算公式,通过测量中性轴上点的剪应变推算出剪切模量。

图6 非对称加载四点弯曲梁试验装置示意图Fig. 6 Schematic diagram of the asymmetrically loaded four-point bending beam test device

由于梁横截面中性轴上点的剪应力τmax=3Q/(2bh),故非对称弯曲加载时梁的侧表面中心点剪应力τ=3P/(4bh),梁侧表面中心点的剪应变γ=ε-45°-ε45°。

(12)

式中,Δε-45°和Δε45°分别为梁侧面中心点的-45°和+45°方向的线应变,且|Δε-45°-Δε45°|=2ε读数。

若采用全桥接法,则式(10)可写为:

G=3ΔP/(8bhΔε读数)

(13)

式中,Δε读数为全桥测量的应变增量读数。

在梁试件的前、后侧表面中心点处粘贴45°应变片。在图6中,该梁施加非对称四点弯曲载荷,测量中心点C的剪应变。梁前后侧表面的+45°和-45°应变片按全桥接法占用应变仪一个通道。

非对称四点弯曲法实施全桥测试,将应变片分别与桥盒连接,并将桥盒接通YD-28A型动态应变仪,连入AdCras信号分析系统。将试件置于支座上按图6所示位置定位,且安放辅助梁,使得加载点位于±45°应变片的中心上方。分3次将1.275 kg的砝码置于辅助梁上,为四点弯曲系统施加载荷,并在每次放置砝码后利用软件记录试件应变值,进行后续计算。

2 结果与分析

2.1 自由板弹性模量和剪切模量的动态测试结果

2.1.1 板试件结果

AZ-1板试件频谱见图7,测算的一阶弯曲频率为105.0 Hz,一阶扭转频率为210.0 Hz。

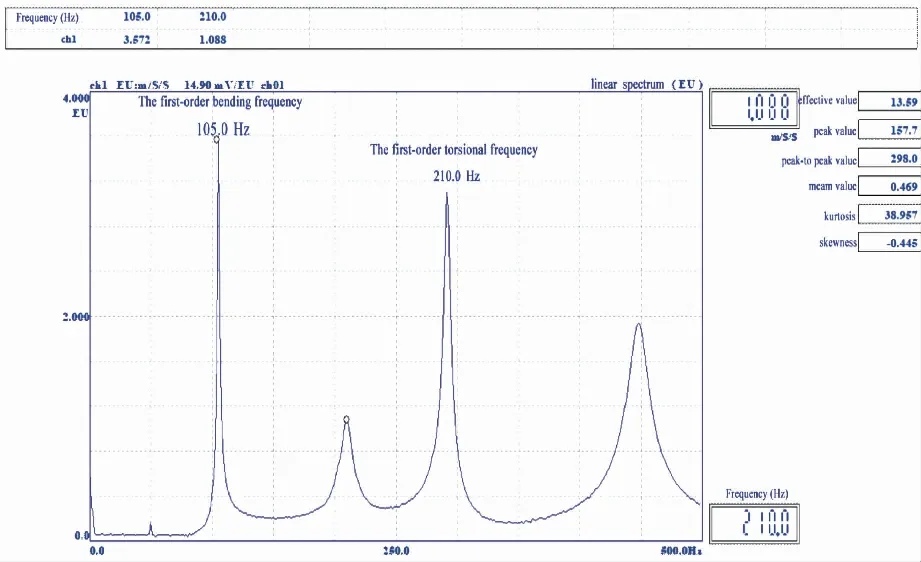
图7 AZ-1频谱图Fig. 7 AZ-1 Spectrogram

通过瞬态试验测得的AZ试件平均弹性模量为12 019 MPa(变异系数5.3%)、剪切模量为1 559 MPa(变异系数6.6%);测得的AH试件平均弹性模量为3 230 MPa(变异系数18.4%)、剪切模量为1 551 MPa(变异系数10.6%)。显然,重组竹纵向板的弹性模量约为其横向板的3.7倍,剪切模量相同。自由板瞬态激励法对横向板的测试结果误差较大,如表1所示,其原因主要在于重组竹的竹束铺装形态不一,有些是呈层层平行铺装状态,有些呈折叠铺装状态,故所得弹性常数变异较大。

表1 重组竹横、纵向弹性模量和剪切模量Table 1 Elastic modulus and shear modulus of horizontal and longitudinal bamboo scrimber

重组竹是由竹束单元构成,按顺纹组坯,经热压(或冷压)胶合而成的板材,其板材结构类似于实木径切板。竹束单元为维管束结构,其排列具有单向性,竹材的顺纹弹性模量较高,重组竹的纵向恰是顺纹方向,它不仅保留了竹材高强度的优点,还克服了竹材壁薄的缺点。且重组竹热压后胶黏界面主要分布在yz和xz面,决定了重组竹顺纹方向的弹性模量Ex将远大于横纹方向的弹性模量Ey,这与试验结果吻合。

由于剪切模量是反映材料某一面内性能的弹性常数,在本试验中测得的剪切模量均为xy面的扭转剪切模量,因此与试件长度方向无关。

2.1.2 梁试件结果

为验证动态测试重组竹试件弹性模量和剪切模量结果的正确性和可靠性,分别从AZ-6和AH-5板试件上锯切出纵梁试件BZ和横梁试件BH,对其进行自由瞬态激励测试,并识别其一阶弯曲频率,计算弹性模量,其结果平均值与原板试件结果对比见表2。BZ-1试件的一阶弯曲频率为398.8 Hz,如图8所示。

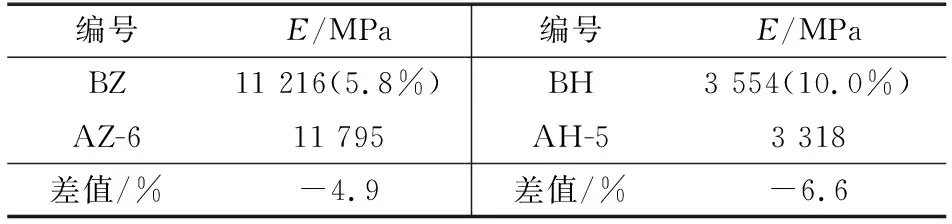
表2 自由梁瞬态激励测试结果与板试件对比Table 2 Comparison of free beam transient excitation test results with board specimens

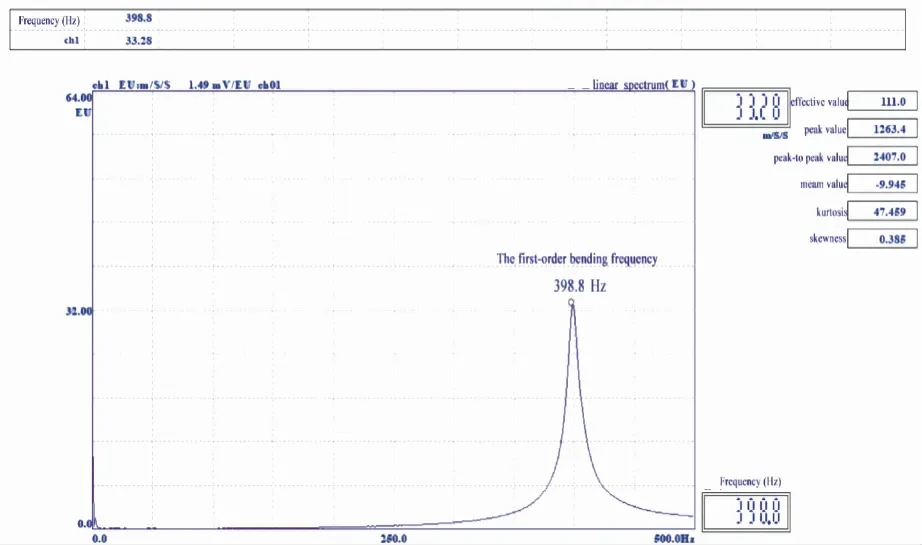
图8 BZ-1频谱Fig. 8 BZ-1 spectrogram

由表2可知,由AZ-6和AH-5加工出的梁试件弹性模量与原板材试件相差不大,且由于横截面较小的原因,测试中未能采集到扭转频率,因此结果未体现剪切模量。对于梁试件也存在纵向弹性模量为横向弹性模量3.1倍的关系,与板试件结果一致。其中,BH试件变异系数较大,与横板试件AH的平均结果类似。这与重组竹的组坯方式有关,竹束顺纹组坯,导致重组竹纵向具有紧密交错的三维网状结构,而横向由于胶层较多,且分布不均,同向材料也存在一定的差距。且其下料位置靠近板材边缘位置的梁,相对更易变形。测试时,5根BZ和BH梁试件的变异系数分别为5.8%和10.0%。其中,在5根BH梁试件中,有3根下料位置位于原板材边缘处。受材质影响,其测得的一阶弯曲频率相对较小,这就导致了BH试件平均结果的变异系数相对较大。

2.2 悬臂板弹性模量、剪切模量和泊松比的动态测试结果

采用悬臂瞬态激励法同步测量重组竹的弹性模量、剪切模量和泊松比,与自由悬挂测试结果相互验证,其频谱如图9所示,得到一阶频率和对应的x向、y向应变量,并计算出相应弹性常数。其悬臂法与自由板法的结果对比见表3。

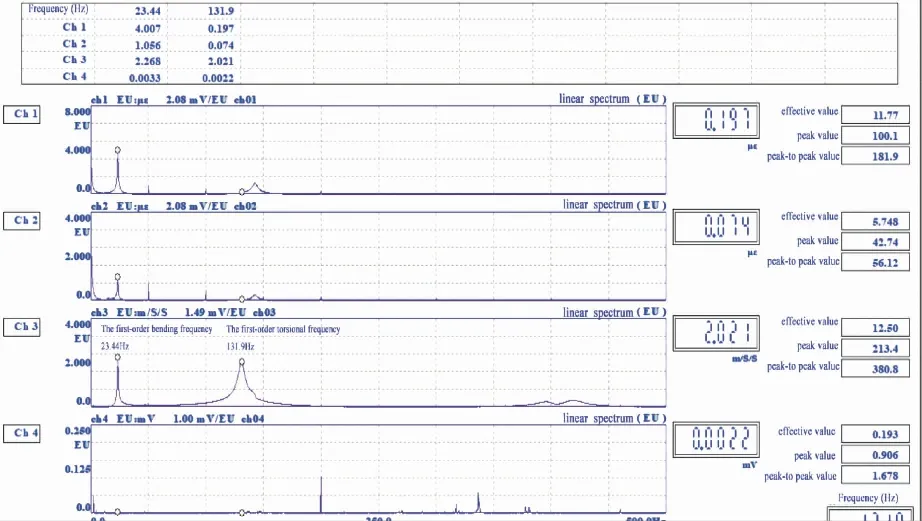
图9 AZ-1悬臂板频谱Fig. 9 AZ-1 cantilever board spectrum

由图9可知,AZ-1试件悬臂瞬态激励的一阶弯曲频率为23.44 Hz,一阶扭转频率为131.9 Hz,x向应变为4.007ε,y向应变为1.056ε。

由表3可知,悬臂法测得的纵向板AZ弹性模量Ex为11 797 MPa、剪切模量Gxy为1 579 MPa,泊松比μxy为0.311,横向板AH弹性模量Ey为3 401 MPa、剪切模量Gyx为1 561 MPa,泊松比μyx为0.105。悬臂板瞬态激励法所测得的结果与自由板瞬态激励测试法结果相吻合,相对误差在5%以内,且泊松比也存在纵向板为横向板3倍的数量关系。此结果表明,动态测试重组竹的E、G、μ是可行的,且测试结果准确。将测试结果代入各向同性验证公式G=E/2(1+μ),其等式不成立,因此认定重组竹为各向异性材料。

2.3 弹性模量、剪切模量和泊松比的静态验证试验结果

为验证动态试验重组竹试件弹性常数的准确性,本研究进行了静态四点弯曲法测试,结果如表4所示。此处主要对BZ和BH 2种梁试件的动态与静态弹性模量进行比较,且测试梁试件的静态泊松比用做判定重组竹是否各向异性的依据。由于对称四点弯测试中,加载实现上表面受压、下表面受拉,故测试结果为拉伸弹性模量和压缩弹性模量的均值,即弯曲弹性模量,而材料的纹理将会由于受力情况不同导致测得的应变量发生变化。为了排除竹束纹理对于重组竹弹性模量的影响,测试中将上、下表面定义为U面和D面进行2组试验,记为Ⅰ和Ⅱ。Ⅰ组试验中U面向上,Ⅱ组试验中D面向上。由表4可知,梁试件由对称四点弯曲试验法测得的纵向弹性模量Ex均值为12 317 MPa,横向弹性模量Ey均值为3 408 MPa。纵梁弹性模量与横梁弹性模量之比为3.6∶1,纵梁泊松比与横梁泊松之比为3.25∶1。测试中翻转试件上、下表面对于测试结果基本无影响。

表4 对称四点弯测试结果Table 4 Summary of symmetric four-point bending test results

此外,为验证动态试验的准确性,以静态非对称四点弯曲法试验测试纵、横向板的剪切模量G。梁试件由非对称四点弯试验测得的纵向板Gxy均值为1 639 MPa,横向板Gyx均值为1 407 MPa,测试结果相差14.2%;Gxy、Gyx测试值的变异系数均小于9%,证实了测试的可靠性。

2.4 E、G、μ动态测试和静态验证试验的对比

梁试件的动态与静态测试结果如表5、6所示。

表5 梁试件动、静态E测试结果Table 5 Dynamic and static E test results of beam specimens

由表5可知,纵向试件自由板瞬态弹性模量比静态弹性模量小2.42%,横向试件动态弹性模量比静态弹性模量小5.22%,可认定动态自由悬挂瞬态激励测试的准确性。纵向试件悬臂板瞬态弹性模量比静态弹性模量小4.20%,横向试件动态弹性模量比静态弹性模量小0.21%,可认定动态悬臂板瞬态激励测试的准确性。各试验对纵、横两向弹性模量的测试偏差相近,证实了各试验的可靠性。

由表6可知,自由悬挂纵向板剪切模量分别比非对称纵向梁小4.88%,悬臂板的纵向剪切模量比非对称四点弯纵梁的剪切模量小3.66%,而横向剪切模量的差值较大,分别相差10.23%和10.94%。此处使用的横向梁试件取自板试件AH-5,其本身动态剪切模量为1 492 MPa,与静态非对称四点弯横梁试件测得的剪切模量仅差6%,也能证明动静态吻合。出现AH试件平均剪切模量与非对称四点弯试件剪切模量相差较大的原因在于AH-5试件本身剪切模量较低,影响了由其制作的BH试件的剪切模量。

表6 板和梁试件动、静态G、μ测试结果Table 6 Dynamic and static test results of G, μ of plate and beam specimens

此外,根据已有研究[28-29]可知,胶合强度对于材料强度也有一定影响。胶合界面的纤维粗糙度、孔隙率、润湿性和胶黏剂的密度都将影响力学强度。对于重组竹来说,其横向胶合界面密布,且竹纤维横向不受力,导致胶合强度对弹性常数(E、G)的影响尤为明显。当前,竹束表面处理仍停留于实验室阶段,实际生产中少有对竹束表面进行处理,这也导致重组竹的胶合强度变异性较大,从而影响材料的E、G,其中,对重组竹横向的影响更为明显。但根据木材领域的研究,木材等天然材料弹性常数的实测值与理论值均存在一定差异,误差一般为15%～25%。因此,动静态测试结果的偏差均在10%证实了动态测试结果的可靠性。

比较不同材料和现有文献中有关重组竹弹性常数的测试结果(表7)[30-32]可知:重组竹纵向弹性模量要优于原生木材,但相比胶合木仍存在一定差距;重组竹横向弹性模量优于木材和胶合木,其主要原因在于重组竹纤维排列紧密,且不具有胶合木中较明显的胶缝。重组竹剪切模量大于木材和胶合木,证明重组竹的抗剪切应变能力优于木材和胶合木。

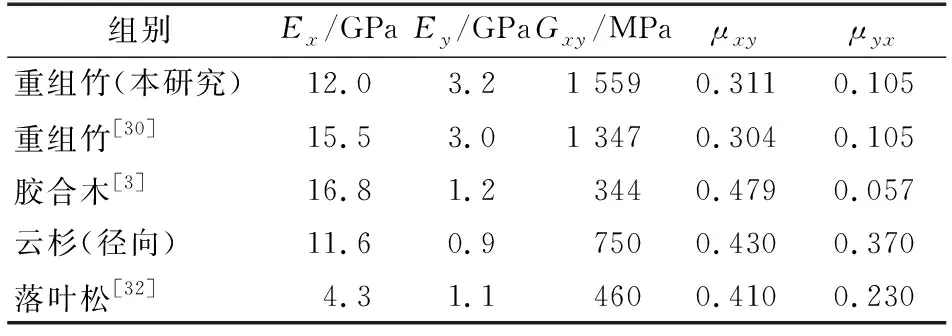
表7 相关测试结果对比Table 7 Comparison of relevant test results

2.5 重组竹的各向异性分析

由重组竹横、纵向弹性模量和泊松比的巨大差异及其纤维排布的单向性,可见本试验中的重组竹为各向异性材料,且各试验对纵、横向弹性模量的测试偏差相近,证实了动态试验的可靠性。

根据重组竹的组坯工艺可以将重组竹分为竹束和胶黏剂,竹束可细分为竹纤维(厚壁细胞组成的维管束结构)和基体(薄壁细胞)。根据已有研究,基体的力学性能弱于竹纤维,但优于胶黏剂。板材纵向为顺纹方向,其弹性模量可以理解为竹纤维、基体与胶黏剂固化后弹性模量的加权;而板材横向为横纹方向,其弹性模量为基体和胶黏剂的加权。从微观三维结构上看,竹纤维以线性结构存在,基体为蜂窝结构,二者间的界面与交接界面是整体结构的薄弱点。这些界面更多地存在于横纹方向,且横向竹纤维不受力,因此纵向弹性模量远大于横向弹性模量。此外,复合材料胶合界面不可避免地存在肉眼不可见的微型空隙,这种现象导致应力不能有效传导,在胶合界面上出现材料薄弱点,严重削弱材料弹性性能。对于重组竹来说,横向胶层密集排布,也将这一缺陷放大,导致变异性更强,出现同规格、同向试件弹性模量差距稍大现象。

3 结 论

1)使用动态测试方法测试了重组竹的纵向弹性模量、剪切模量和泊松比,其分别约为11 797 MPa,1 579 MPa和0.311,满足GB/T 40247—2021中结构用重组竹的技术要求。

2)重组竹为各向异性材料。本研究中测得的重组竹纵向E、G变异性较小,横向力学性能变异性较大。其纵向弹性模量为横向的3～4倍,纵向泊松比为横向的3倍,横、纵向的剪切模量相近。

3)本研究将动态测试结果与静态试验结果进行比较后,观察到二者对弹性模量、剪切模量以及泊松比的测试结果有着很高的一致性。该现象验证了动态测试的准确性。

4)动态测试重组竹弹性常数的方法相比于传统测试方法具有快速、简便、重复性好和精度高的优点。