介电弹性薄膜翼型的增升效应机理

康伟，胡仕林，王彦清

西北工业大学 航天学院，西安 710072

微型飞行器一般是指最大尺寸不超过15 cm、重量为10～100 g、有效载荷为20g以上、飞行速度为30～60 km/h的飞行器［1］，在军事侦察，战争危险估计、目标搜索、通信中继等领域具有重要的应用价值。微型飞行器在低雷诺数（Re＜2×105）飞行时所面临的问题逐渐显现出来，如翼型的升力较低，翼型表面剪切层的分离以及微型飞行器在大攻角时非定常效应显著等。

为了改善微型飞行器在低雷诺数下的气动特性，达到增升减阻、改善操稳的目的，人们注意到了自然界中蝙蝠可以通过控制肌肉收缩与扩张来主动改变翼翅形状以改善其飞行品质，而这种特征若应用于飞行器上则有助于改善飞行器的气动特性。电活性聚合物材料为这种思路提供了仿生途径与手段。作为电活性聚合物材料的代表，介电弹性高聚合物材料能够通过软电极材料在薄膜上下表面形成电荷差。这些不同的电荷相互吸引，迫使薄膜沿厚度方向压缩，随后导致平面拉伸变形。通过将介电弹性高聚合物材料应用到飞行器机翼蒙皮上，研究人员发现这种材料能够适应气流的变化进而改善剪切层内气流的附着效果，且随着外加电压的不同，飞行器翼型的形状能够主动变形。在其变形过程中，体现了2种主要的变形模式：气动弹性效应与来自于通过施加电场对薄膜材料形状的主动变形，而这2种效应使得介电弹性薄膜翼型在低雷诺数下的流动是一个综合考虑流场-电磁场-结构场的多物理场耦合问题。

目前针对柔性薄膜翼与介电弹性薄膜翼的研究主要采用试验与数值模拟2种方法。在实验方面，Song等［2］研究了柔性薄膜翼在不同流动状态下的行为特征，发现在给定雷诺数下，柔性薄膜翼屈曲程度与振动模态均随着来流攻角的增大而增大；Rojratsirikul等［3］对二维柔性薄膜翼进行了研究，发现柔性薄膜翼的振动有助于激发附面层涡流的产生从而改善薄膜翼的气动特性；随后Rojratsirikul等［4］又对柔性薄膜翼振动模式进行了研究，发现柔性翼表面的弦向振动与尾涡脱落频率存在一定的耦合关系。Sun等［5］将柔性薄膜材料直接应用到NACA0012翼型上，发现薄膜材料厚度与杨氏模量对翼型在失速攻角附近的气动特性有着直接的影响。在主动控制的研究上，Hays等［6］研究了介电弹性薄膜翼在不同外加电压下的气动特性，发现采取主动控制的介电弹性薄膜翼相对于被动控制能够表现出更大的升力系数；Curet等［7］对介电弹性薄膜翼施加正弦电压，发现施加的电压频率与薄膜的基频或第一谐波频率出现共振时薄膜翼的升力系数达到最大。

在数值模拟方面，Lian等［8-9］针对柔性薄膜机翼建立了气动弹性耦合计算策略。研究发现，薄膜翼表面存在的高频率振动能够有效地提升升力；Gordnier［10］针 对 柔 性 薄 膜 翼 建 立 了 六 阶Navier-Stokes（N-S）求解器，并与非线性结构响应的膜结构模型相耦合共同形成了一个高保真度的计算耦合策略，研究发现，随着来流攻角的增大柔性薄膜翼振动模式复杂程度大大增加，非定常特性越来越明显，并且还发现结构的振动频率与非定常流涡脱落的频率相似；Molki等［11］结合商业流场分析软件Fluent构建了对柔性薄膜翼的流固耦合分析框架，研究发现，柔性薄膜翼相对刚性翼表面的分离泡更均匀，气流分离点更靠后。在薄膜翼主动控制方面，Buoso等［12-13］采用商业软件Abaqus与StarCCM+对柔性薄膜翼建立了主动控制下的综合性数值计算方法，研究发现在电压驱动下，二维机翼气动特性提升了15%。国内近年来对柔性薄膜翼的低雷诺数流动机理开展了数值与试验研究，如中国航天空气动力技术研究院白鹏等［14］研究了低雷诺数翼型层流分离非定常效应流动结构，南京航空航天大学的肖天航等［15-16］针对柔性翼拍动飞行开发出了一种基于CFD/CSD耦合的双向流固耦合方法。本文针对低雷诺数薄膜翼提出了局部柔性翼面的自适应流动控制方法。通过数值分析与试验研究［17-19］，发现局部柔性翼型的耦合振动会与非定常涡脱落频率发生同步，诱发前缘涡在上翼面的连续形成，保持上翼面的负压区，提高机翼的气动特性。

介电弹性翼型的流动控制涉及了介电材料的力电特性、柔性结构与非定常低雷诺数涡流的耦合作用［20-21］。将介电弹性高聚合物材料应用于翼型上的研究与气动特性分析仍处于起步阶段，对其多物理场耦合机理有待进一步分析。

本文基于CFD/CSD耦合方法建立了介电弹性薄膜翼型的耦合分析方法，构建了一个综合考虑流场-结构-电磁场的耦合模型，对介电弹性薄膜翼型进行了气动特性分析，对介电弹性薄膜翼型的增升效应进行机理分析，为主动控制介电弹性薄膜翼型以进一步改善气动特性提供了技术支撑。

1 介电弹性薄膜翼型

层流翼型表面的气流往往在靠近翼型前缘部分发生分离，为了利用柔性结构改善翼型表面的气流分布，在NACA0012翼型的基础上选取上表面的3/4作为局部柔性部分，这部分的翼型由介电弹性高聚合物材料构成，从而形成如图1所示的介电弹性薄膜翼型。翼型弦长为300 mm，柔性部分厚度为2 mm，结构材料为介电弹性薄膜材料VHB4910，其弹性模量为341 500 Pa，材料密度为402.3 kg/m3，可通过两端的固定约束向其输入外加电压以达到不同的控制面效果。

图1 介电弹性薄膜翼型Fig.1 Dielectric elastic membrane airfoil

2 数值仿真计算模型

2.1 结构场建模与求解

介电弹性薄膜结构采用Neo-Hookean材料本构模型以及理想介电弹性聚合物假设，则介电弹性薄膜的Cauchy应力张量可以表示为

式中：σM表示由于薄膜结构特性引起的应力变化；σDE为由于介电特性引起的力电耦合变化。

基于美国哈佛大学锁志刚教授研究组提出的可变形电介质的热力学理论框架［22-23］，介电弹性体的力电耦合效应所贡献的Maxwell应力张量可以表示为

式中：EEF=F-T表示当前构型下的电场矢量，F为形变变形张量；ε为真空介电常数与材料相对介电常数的乘积表示参考构型下的电场矢量，V表示施加在结构上电压值，t表示结构的厚度，nref表示薄膜结构的单位法向量；定义电场等效弹性模量为用以表征外加电场对结构的力电耦合效应。

介电弹性体的应变能函数表示为

式中：μ=分别是结构的线性弹性模量与泊松比；J=det(F)。

在忽略结构阻尼的前提下，由虚功原理可得

式中：ρs为结构密度；u为结构位移；σ为考虑了力电耦合的结构内应力张量；fbody为结构所受的体积力；fCFD为作用在结构表面的气动力。

采用二阶四边形有限单元对结构域离散。单元内节点位移矢量u可以表示为

式中：指数A=1，2，…表示单元的节点；uA为节点位移；NA是形状函数。

采用Galerkin方法求解式（4）可以得到离散形式的结构控制方程为

该方程组可以通过显式Newmark方法对时间项进行离散，进而与流体CFD求解器耦合采用Newton-Raphson方法求解得到结构响应。

2.2 流场建模及求解

考虑带有网格运动的非定常可压缩流动控制方程的积分形式可以表示为

式中：Ω(t)为控制体的体积；∂Ω(t)为控制体的边界面。这是由于网格是运动的，所以控制体的体积和表面积都是时间的函数。Q为守恒变量向量；F*为守恒变量的对流项；Fv为黏性耗散项；网格运动矢量为[ug，vg，wg]T。各项的具体形式为

针对低雷诺数非定常非线性流动采用有限体积法求解N-S方程，空间离散格式采用具有高黏性分辨率的ROE格式，并采用MUSCL插值方法获得三阶空间离散精度。空间精度的提高有助于对黏性流动中涡结构的生成与演化的精确捕捉。时间推进采用LUSGS隐式时间推进方法，来描述薄膜翼绕流中的流动分离、涡系结构的非定常演化。利用高性能集群对非定常流动进行大规模计算。

图2给出了介电弹性薄膜翼型的流场计算网格图。采用O型结构化网格进行剖分，远场范围为40倍翼型弦长，网格数为257×55，第1层网格高度为1×10-5。

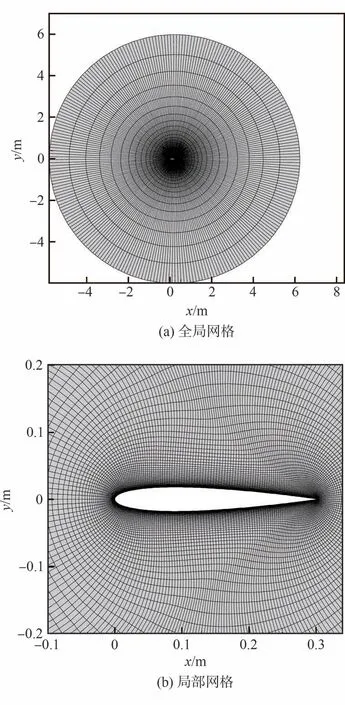
图2 介电弹性薄膜翼流场计算网格Fig.2 Computational grid of dielectric elastic membrane airfoil

2.3 流场-结构-电磁场耦合策略

按物理场的不同将耦合场求解器分为介电弹性体外加电压引起的Maxwell应力模块，结构求解模块和流体求解模块3个部分。图3给出了介电弹性薄膜翼型气动-电磁-结构耦合的流程。首先，用Maxwell应力张量量化介电弹性体的力电耦合效应，作为结构求解器的输入。而后采用松耦合方式处理结构域与流体域之间的耦合关系，2个物理域通过交界面交互数据。

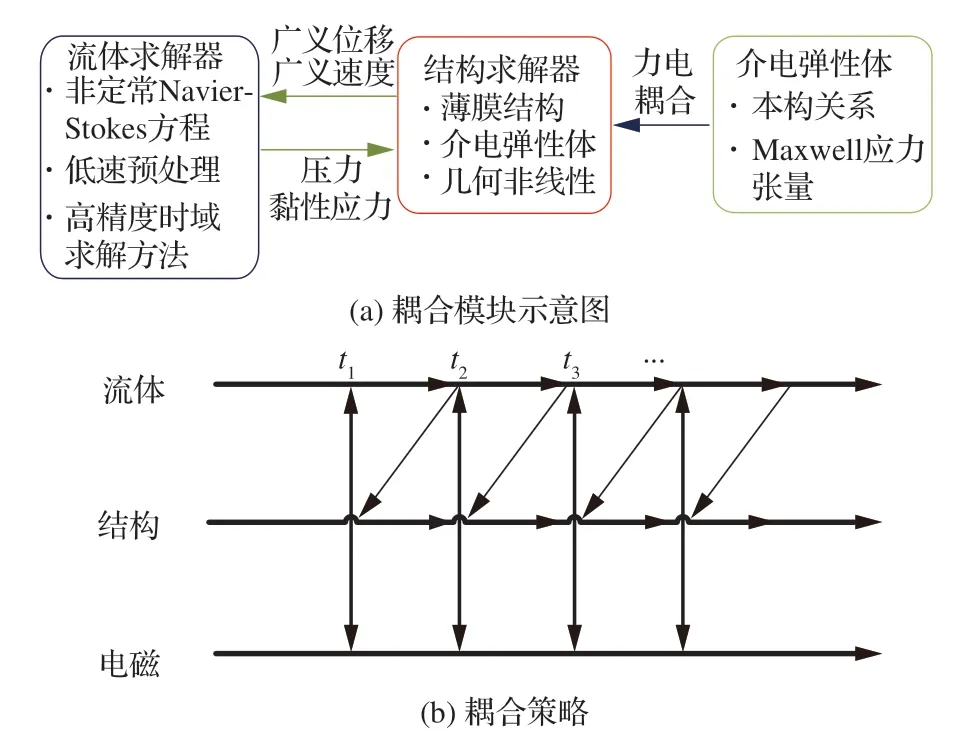
图3 介电弹性薄膜翼气动-电磁-结构耦合基本流程Fig.3 Flow chart of aero-electromagnetic-structural coupling of dielectric elastic membrane airfoil

2.4 模型验证

2.4.1 介电薄膜结构的力电耦合验证

为了验证所建立的力电耦合模型的准确性，与Sanchez等［24］的薄膜结构计算结果进行了对比。结构材料为介电弹性薄膜材料VHB4910，其相关结构参数参见表1。图4给出了在0.4 Pa的外加压力与外加电场等效弹性模量分别为2×106Pa与6×106V/m下的薄膜结构变形情况。从图4中可以看出不同外加电压越大，结构的变形越大。这说明外加电场所带来的力电耦合效应起到了减弱结构弹性的效应。同时，从图中与已有的文献结果比较可以看出所提方法能够准确描述介电弹性薄膜结构的响应特性。

表1 结构参数列表Table 1 List of structural parameters

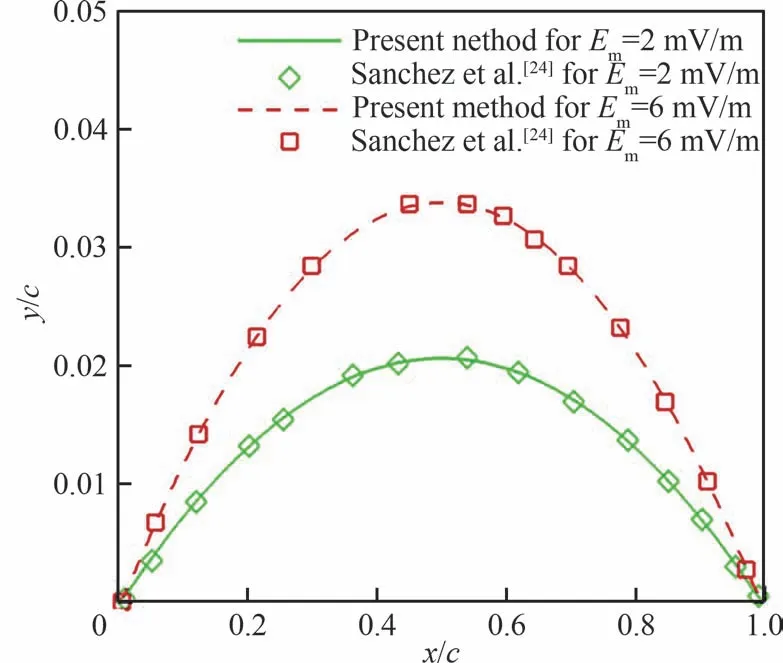
图4 薄膜结构在0.4 Pa压力下的变形比较Fig.4 Deformation of membrane at pressure 0.4 Pa

2.4.2 流固耦合验证

为验证本文所提方法在气动弹性问题上的准确性，采用Rojratsirikul的流固耦合模型［2］进行验证。该模型为两端固支的膜翼，流体与结构的相关参数如表2所示。

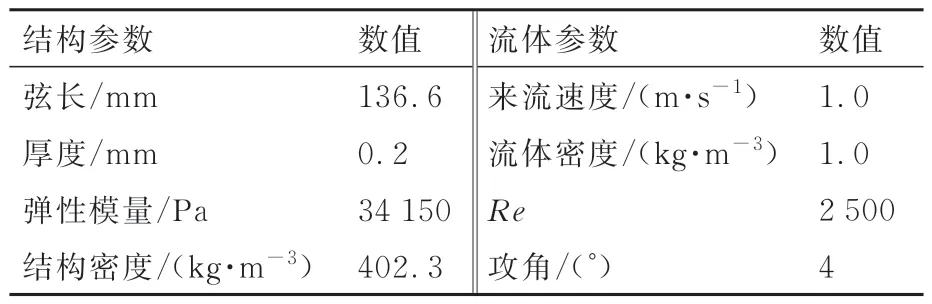
表2 流体与结构的相关参数Table 2 Parameters of fluid and structure

图5和图6给出了攻角为α=4°与Re=2 500时膜翼的流固耦合响应。与Buoso等［12］的计算结果对比看出膜结构的时均变形和翼面压强系数Cp与文献吻合良好。膜结构的时均变形的相对最大偏差仅为2.75%，说明了所提模型的可靠性与准确性。

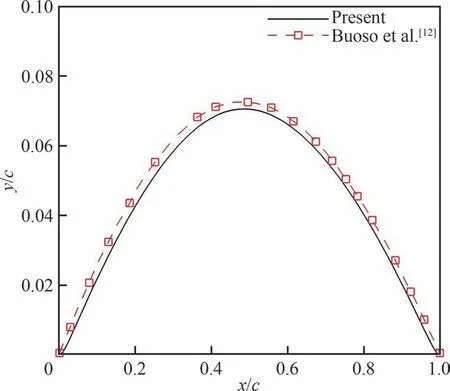
图5 Re=2 500和α=4°时智能薄膜翼的时均变形比较Fig.5 Mean deformation of membrane at Re=2 500 and α=4°

图6 Re=2 500和α=4°时智能薄膜翼的压强分布比较Fig.6 Pressure coefficient over membrane at Re=2 500 and α=4°

3 结果与分析

3.1 变形与振动对气动特性的影响

图7给出了介电弹性翼型上表面弹性部分在雷诺数为5 500，外加电压为0.1 kV时不同攻角下的时均位移变形。可以看到，介电弹性翼型的变形在翼型的前1/3部分表现为下凹变形，在后2/3表现为上凸变形。在攻角2°～8°范围内，翼型的时均变形基本没有变化，而在8°以后，翼型的“下凹”变形与“上凸”变形对应的变形量急剧增加，而在10°～12°范围内，翼型的变形又基本保持不变，但在攻角升高到14°时，翼型的时均变形再次增加。

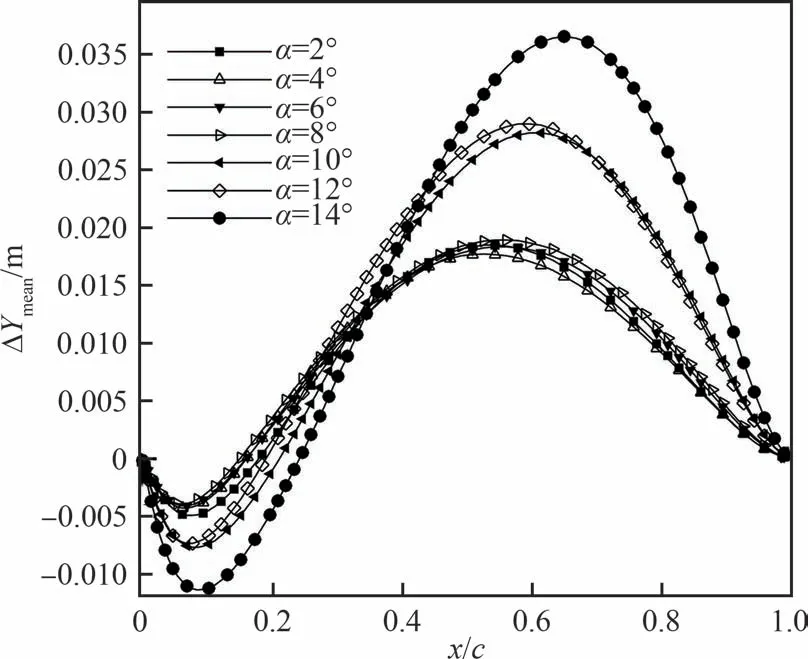
图7 介电弹性翼型不同攻角下的时均位移变形（Re=5 500，V=0.1 kV）Fig.7 Time-average deformation of dielectric membrane airfoil with different angles of attack at Re=5 500 and V=0.1 kV

图8给出了介电弹性翼型上表面弹性部分y方向位移振动幅度随攻角的变化。从图中可以看到，介电弹性翼型的振动幅度在低攻角范围内（2°～8°）较小，振动在攻角8°以后开始显著增加，在10°时达到最大，而后振动幅度有所下降，但仍保持在一个较大的振动幅度。

图8 介电弹性翼型在不同攻角下的振动幅度（Re=5 500，V=0.1 kV）Fig.8 Vibration amplitude of dielectric membrane airfoil with different angles of attack at Re=5 500 and V=0.1 kV

为了探究介电弹性薄膜翼型的弯度变形与振动效应分别对翼型升力的影响程度，本文将介电弹性翼型与刚性翼型、刚性弯度翼型在相同来流条件下进行对比，其中刚性弯度翼型为介电弹性翼型在对应来流状态的时均形状，旨在对比明晰振动效应对翼型气动特性的影响。

图9（a）给出了3种翼型在攻角为2°时的表面时均压强分布。介电弹性翼型与刚性弯度翼型上表面时均压强分布在靠近前缘的部分较刚性翼型有所提高。在图中表现为“下压”分布，甚至出现了上表面压强小于下表面压强的现象。联系图7可知，介电弹性翼型前缘部分发生了下凹变形，故造成了介电弹性翼型在靠近前缘部分的翼型弯度由正转负，从而导致其上表面时均压力的畸形分布。而在翼型上表面的后缘部分，3种翼型的压力分布基本吻合，可见在低攻角范围内，翼型弯度的变化对前缘压强分布有一定的影响。

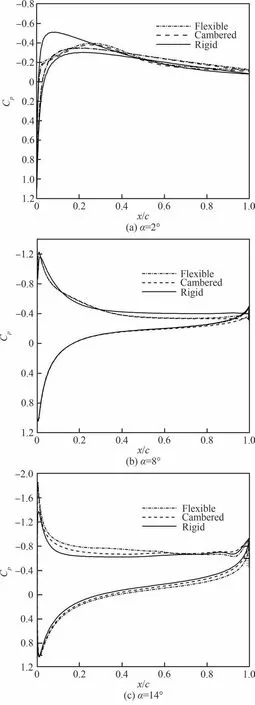
图9 3种翼型在不同攻角下的翼表面时均压力分布（Re=5 500，V=0.1 kV）Fig.9 Time-average pressure distribution of three airfoils with different angles of attack at Re=5 500 and V=0.1 kV

图9（b）给出了3种翼型在8°时的表面时均压强分布，可以看到介电弹性翼型与刚性弯度翼型上表面前缘部分的“下压”现象消失。当攻角在2°～8°时，介电弹性翼型时均变形基本保持不变，弯度维持不变，同时前缘压强分布发生了明显好转，这是由于前缘负弯度带来的负面效果与由于攻角增大带来的正面效果达到了平衡，从而促使3种翼型的压强分布基本保持一致。

图9（c）给出了3种翼型在14°时的表面时均压强分布。在翼型的上表面，介电弹性翼型吸力峰值明显高于其余2种翼型。通过比较刚性翼型与刚性弯度翼型，可以发现后者在大攻角下表现出来较大的吸力，且翼型后缘的弯度在大攻角下有明显的增大，虽然前缘部分下凹得更严重，但总体上翼型后缘弯度在翼型整体弯度中占据主导作用，故弯度翼型上表面表现出更大的吸力分布。

通过比较介电弹性翼型与刚性弯度翼型，可以发现前者在大攻角下表现出更大的吸力，虽然两者时均变形均相同，即弯度对2种翼型压强分布的影响是相同的，但是介电弹性翼型存在振动效应。结合图8振动变形来看，在大攻角范围内，介电弹性翼型的振动相对于小攻角时要更剧烈，因而在翼型上表面表现出更大的吸力，这同时也解释了在小攻角范围内，介电弹性翼型与弹性翼型的压强分布基本保持一致的现象，其原因在于小攻角下介电弹性翼型振动效应不明显，只有在大攻角下振动效应才会表现出一定的作用。因此，影响介电弹性翼型表面压强分布的主要原因有2个：① 翼型弯度的变化；② 翼型的振动效应。其中翼型弯度在攻角较小时甚至表现出了负弯度，而翼型的振动效应只有在攻角较大时才对翼型表面压强分布起到重要影响。

为了进一步探究介电弹性薄膜翼型弯度变化与振动效应对翼型增升的具体影响，图10对比了3种翼型的升力曲线。介电弹性翼型与刚性弯度翼型在攻角为2°～8°范围内基本保持线性变化，而刚性翼型在2°～8°范围内由于非稳态尾缘分离气泡的存在表现出非线性变化。注意到攻角在2°时，介电弹性翼型与刚性弯度翼型升力系数均比刚性翼型要低，结合之前对于表面压强的分析，可知是由于前缘出现负弯度造成的；而后随着攻角慢慢增大，后缘弯度的增升效应逐渐起主导作用，从而使得3种翼型的升力线基本保持一致；在攻角＞8°以后，介电弹性翼型与刚性弯度翼型的升力线开始分离，前者升力线斜率明显增大，而后者几乎没有发生改变，最终导致了介电弹性翼型在大攻角范围内的升力系数要大于刚性弯度翼型，故可以认为在攻角超过8°以后，介电弹性翼型的振动效应通过改变升力线斜率从而开始起到明显的增升作用。当攻角在14°时，介电弹性翼型相对刚性翼型增升12.33%，相对刚性弯度翼型增升4.45%，其中弯度变化对增升的贡献为59.44%，振动效应对增升的贡献为40.56%，两者贡献比约为3∶2。而对于刚性翼型，其在大攻角状态下由于流动分离而表现出非线性现象。

图10 3种翼型升力系数曲线（Re=5 500，V=0.1 kV）Fig.10 Lift coefficient curves of three airfoils at Re=5 500， V=0.1 kV

为了明晰振动效应对流动结构的具体影响以及增升机制，图11和图12分别给出了攻角在8°和10°时3种翼型在一个脉动周期内的流动结构。

图11 3种翼型的流动结构对比（Re=5 500，α=8°）Fig.11 Comparison of fluid structure at Re=5 500 and α=8°

图12 3种翼型的流动结构对比（Re=5 500， α=10°）Fig.12 Comparison of fluid structure at Re=5 500 and α=10°

当攻角为8°时，刚性翼型上表面气流在距离前缘大约1/4处的地方开始分离，而由于弯度的存在，刚性弯度翼型与介电弹性翼型上表面的气流分离点较刚性翼型要靠后，但分离点的后移并没有在实质上改变涡旋结构。当攻角为10°时，对于刚性弯度翼型，同样可以看到分离点的后移，但与攻角在8°时一样，其并没有在本质上改变涡旋结构；而对于介电弹性薄膜翼型，可以看到在前缘处形成了明显的分离气泡，而后随着涡的后移，气流不断分离而后再附在翼型表面，形成了近乎连续分布的分离泡，与刚性弯度翼型相比较，可以发现如此密集的涡流分布并不是由于翼型弯度的改变，而是由于介电弹性翼型振动效应的加强，这种振动效应在实质上改变了翼型的流动结构，从而使得介电弹性翼型升力增大。

为了进一步探究翼型振动特征与流场结构之间的关系，图13对比了刚性翼型与介电弹性翼型的流场、结构主频率随攻角的变化。其中取介电弹性翼型表面变形部分3/4处点的y方向位移频率作为结构场频率，并取对应部分剪切层边界位置的压强频率作为流场频率。可以发现当攻角在α=2°，4°，10°，12°，14°时，介电弹性翼型流场主频率与结构场振动频率相同；同时在大部分攻角下，介电弹性翼型流场主频率与刚性翼型的流场主频率均相同，由此可以看到介电弹性薄膜结构与流场结构发生了共振，从而使得翼表面的涡分布相对刚性翼型更密集，进而促使介电弹性翼型获得更大的升力。

图13 流场主频率与结构场主频率比较Fig.13 Comparison of dominant frequency of fluid and membrane structure

3.2 外加电压的影响

通过3.1的分析，可以发现介电弹性翼型的振动效应在攻角＞8°时对翼型产生增升作用，而通过改变介电弹性体材料两端的外加电压可以改变介电弹性体振动模式从而实现对翼型的主动控制。

为了比较不同外加电压下对介电弹性翼型升力的影响，选择攻角为14°的增升效果最显著的情况加以研究。图14给出了翼型在攻角为14°时，外加电压在0～0.9 kV范围内的时均升力系数比较。可以从图中发现，外加电压在0～0.8 kV范围内的翼型均表现出相对于刚性翼型的增升效果，且当V=0.1，0.3，0.5，0.7 kV时增升效果尤为显著，在V=0.3 kV时甚至达到了18.19%的增幅。介电弹性翼型升力系数随着外加电压的增大呈现出一个近似于周期性的变化，但这种周期性变化只在特定的外加电压范围内才能表现出来。当V=0.9 kV时，升力系数急剧下降，可能是因为外加电压过大造成薄膜电击穿从而导致介电弹性翼型逐渐失稳。

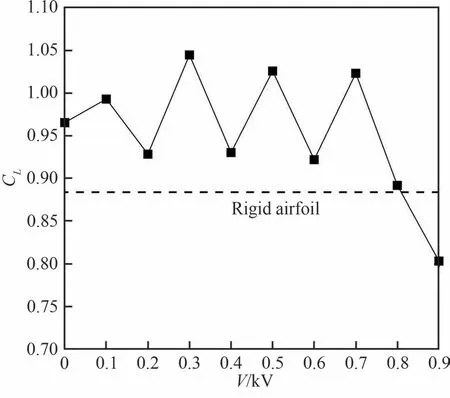
图14 介电弹性翼型在不同外加电压下的时均升力系数（Re=5 500，α=14°）Fig.14 Time-average lift coefficient of dielectric membrane airfoil with different actuated voltages at Re=5 500 and α=14°

图15比较了流场主频率与振动主频率的关系，并与刚性翼型的流场主频率进行了对比。可以看到外加电压在0～0.9 kV范围内，所有外加电压下介电弹性薄膜翼型的一阶流场主频率与一阶振动主频率均相同。在二阶主频的范围内，可以进一步发现对于外加电压为0.1、0.3、0.5、0.7 kV的介电弹性薄膜翼型，薄膜翼振动的二阶主频与流场的二阶主频均相同，而当外加电压为0.8 kV时，虽然二阶振动主频率与流场二阶主频率也发生了重叠，但其二阶频率并未达到对应刚性翼型的流场二阶主频率，结合介电弹性翼在0.8 kV时的增升效果，可知当振动的二阶主频与流场的二阶主频相同且不小于对应刚性翼型的流场二阶主频时，介电弹性翼型的升力才具有明显的增升效果。当V=0.2，0.4，0.6 kV时，其结构与流场的二阶主频没有发生直接的重叠，增升效果不明显。

图15 振动频率与前两阶频率比较（Re=5 500，α=14°）Fig.15 Comparison of first two frequencies of flow at Re=5 500 and α=14°

4 结 论

通过对介电弹性膜翼的增升机理进行研究，得出以下结论：

1） 提出了基于CFD/CSD耦合的介电弹性薄膜翼型的耦合分析方法，发展代码自主可控的气动-力-电耦合求解方法，对力电耦合与流固耦合模型的准确性进行了验证。

2） 介电弹性薄膜翼型增升效应在不同的攻角状态下表现不同。在攻角为8°以前，其相对刚性翼型的增升效果并不明显，而在攻角超过8°以后，柔性薄膜结构通过与流场结构发生共振，明显改善了翼表面涡流分布，有效地提高了翼型的升力。在攻角为14°时，翼型升力提高了12.33%。在攻角为14°时，弯度变化与振动效应对增升的贡献比为3∶2。

3） 对于介电弹性薄膜翼型，当外加电压使得柔性薄膜结构与流场结构在前两阶频率上发生重叠，且二阶主频不小于对应刚性翼型二阶主频时，介电弹性薄膜翼型相对刚性翼型增升比均在10%以上。

下一步将重点研究影响介电弹性薄膜翼型升力变化的参数化方法，从而实现利用外加电压对介电弹性薄膜翼型的主动控制。