基于混合状态机的航天器自主绕飞多模态控制

2023-10-17李敏袁利魏春岭

航空学报 2023年18期

李敏，袁利，魏春岭

1.北京控制工程研究所，北京 100190

2.空间智能控制技术重点实验室，北京 100190

3.中国空间技术研究院，北京 100190

近年来，在轨服务技术逐渐成为各国航天领域关注的重点方向。当在轨服务对象为非合作目标时，由于相关先验信息少，需要对其进行跟踪观测，识别其特征后才能开展后续的服务过程。通过绕飞从不同方位、不同光照条件下获取目标的观测信息是一种有效的跟踪观测方式，能够提炼更加全面的目标特征。然而绕飞观测是一个长时间过程，期间航天器可能面对许多未知不确定的情况，因而需要航天器控制系统具有自主控制能力，根据系统运行状态改变控制策略，调整控制器参数，从而应对不确定性情况，自主完成绕飞观测过程［1-2］。

针对自主绕飞控制问题，目前已经有一定的文献研究了相关控制方法。文献［3］针对不具备主动机动能力目标的绕飞控制问题，对近圆和椭圆轨道上的航天器间相对运动进行了分析和建模，求解了常值推力下相对运动模型的解析解，通过模型预测方法获得了全状态预期偏差，设计了相对位置保持和循迹绕飞任务下的全状态反馈控制器。文献［4］研究了对无控旋转目标的强迫绕飞控制问题，建立了视线坐标系的三维相对运动模型，并通过坐标变换将对目标绕飞的三维控制问题转化视线坐标系旋转平面内的二维控制问题，提出了模糊切换增益调节的滑模绕飞控制策略。文献［5］研究了对椭圆轨道上的非合作目标长期绕飞控制问题，建立了安全约束下的绕飞轨道非线性规划模型，采用最优控制理论设计了燃料最优的绕飞轨道保持控制策略。文献［6］研究了有限推力下的航天器轨道绕飞与保持控制问题，建立了线性化后的动力学系统模型，结合线性二次最优控制理论设计了最优反馈绕飞控制器。文献［7］利用T-H方程建立了航天器绕飞相对运动控制系统模型，基于模型参考控制思想，结合状态反馈和参数化前馈跟踪补偿设计了模型参考绕飞轨迹跟踪控制器。文献［8］建立了航天器控制任意方位快速绕飞相对运动模型，设计了基于期望相对绕飞轨迹的跟踪控制策略。

然而需要指出的是上述大多数结果中绕飞对象是不具备主动机动能力的目标，且控制策略单一，任务模式简单［9］。当目标具有主动机动能力时，由于其机动策略未知，可能会给绕飞过程会带来很多不确定性，甚至会给航天器造成碰撞风险。另一方面，空间环境的日益拥挤也可能会给航天器绕飞过程中带来了一定的碰撞风险，因此航天器控制系统需要具备保障航天器在完成自主绕飞任务的同时还能保障航天器与非合作目标以及其他空间目标之间的安全性的能力［10-11］。此外，在绕飞过程中，为了能够对目标进行有效观测，需要根据光照条件来自主决策观测窗口，在光照条件好的地方进行长时间观测，在光照条件差的地方不进行观测，其任务模式是复杂的，需要根据不同任务模式来自主改变航天器行为状态［12］。因此，针对具有主动机动能力的非合作目标进行绕飞，由于面临许多不确定性且任务模式复杂，需要航天器具备可靠且更加自主的控制能力，能够根据实际情况来选择合适的控制策略和参数，控制自身行为状态，例如相对位置保持、绕飞转移、碰撞规避等，即具有多种模态控制能力，来实现既定的控制任务目标的同时还能够有效规避空间目标的碰撞威胁事件。有限状态机能够有效描述系统运行逻辑和状态，并能够通过设计系统状态之间的转换函数来实现对系统运行状态之间切换的监控和决策管理，控制策略和控制参数的选择本质上也是根据系统运行状态来在已设计好的策略和参数当中进行切换，因此有限状态机整提供了一种可借鉴手段。综上所述，航天器自主绕飞多模态控制问题还是一个开放的问题，目前还没有得到较好的解决。

本文研究了对具有主动机动能力的非合作目标自主绕飞控制问题，提出了基于混杂系统的自主绕飞多模态控制方法。首先，建立了混杂系统模型，根据自主绕飞任务目标和安全性分析，定义了远程接近、近程接近、相对位置保持、绕飞转移、碰撞规避、撤离等状态以及各个状态下的控制目标；为了实现各个状态之间的协调，以状态机为基础建立各个状态的自主管理和监控方法，定义了状态之间相互转化的函数关系。其次，根据不同状态的控制目标，设计相应的控制策略，实现对混杂系统的多模态控制。最后，对提出的自主绕飞控制方法进行了仿真验证，仿真结果说明了所提出的方法的有效性。

1 自主绕飞控制系统建模

对非合作目标绕飞的全过程自主控制是一个非常复杂的过程，行为状态根据与目标之间的相对运动关系以及任务目标可分为远程接近、近程接近、相对位置保持、绕飞转移、碰撞规避和撤离6个状态。在绕飞的过程，航天器既要能够通过决策对行为状态转换进行自主控制，又要能够根据决策给出的行为状态对相对运动关系进行控制，被控对象特性混杂，属于一类典型的混杂系统，难以仅用微分方程建立系统模型，本文用混合状态机建立混杂系统模型［13］。自主绕飞控制系统的混合状态机模型主要分为3个部分：有限状态机模型、相对运动模型以及相互之间的转换函数。

1.1 有限状态机模型

在对非合作目标自主绕飞观测过程中，正常情况下，主要为远程接近、近程接近、相对位置保持、绕飞转移和撤离5个行为状态，其状态机如图1所示［14］。

图1 无碰撞风险下的自主绕飞过程Fig.1 Process of autonomous fly around without collision risk

然而，近年来随着空间碎片的增加以及大型星座的建造使得轨道空间越来越拥挤，航天器面临的碰撞风险激增。此外，非合作目标自身具有机动能力，也可能给航天器带来碰撞风险，使得航天器的安全性受到威胁。为了能够使得航天器在轨运行过程中能够有效规避碰撞威胁事件，从安全性考虑，需要引入碰撞规避状态，即检测到碰撞风险时，对碰撞威胁进行规避。由于航天器为高价值资产，任何时候都不希望出现事故，因此碰撞威胁规避的优先级最高，即任何行为状态下，一旦检测到碰撞风险都需要进入碰撞威胁规避行为状态。因此，在原来的基础上，对非合作目标绕飞过程设计为由远程接近、近程接近、相对位置保持、绕飞转移、碰撞规避和撤离6个状态组成的新状态机，如图2所示。

图2 对非合作目标自主绕飞状态机模型Fig.2 State machine model of autonomous fly-around for non-cooperative target

T={Ti} (i=0，1，2，3，4，5)表示状态之间的转换函数，决定航天器6个行为状态的转换。另外，为了方便后续描述，定义Q={q0，q1，q2，q3，q4，q5}分别表示表示远程接近、近程接近、相对位置保持、绕飞转移、碰撞威胁规避和撤离等6个行为状态。

1.2 相对运动模型

为了方便描述航天器的相对轨道运动行为，首先构建相关坐标系，如图3所示。其中：FI表示地心惯性坐标系，原点为地心，X轴指向春分点，Z轴指向天球北极，Y轴与其它两轴构成右手坐标系；Fo表示参考质点轨道坐标系，原点即为参考质点，Zo轴从参考质点指向地心，Yo轴垂直于瞬时轨道平面并指向轨道面的负法线方向，Xo轴指向与其他两轴构成右手坐标系。图3中航天器P和航天器E分别为绕飞航天器和非合作目标，航天器C为空间其他目标，存在一定的碰撞风险。

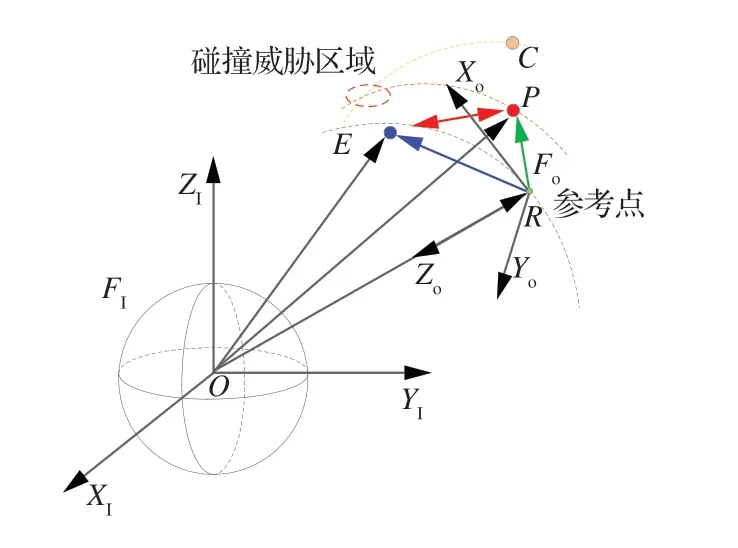
图3 相关坐标系Fig.3 Relevant coordinate system

假设航天器E具有主动机动能力，在不考虑轨道摄动及其他外部扰动情况下，根据文献［15］，可知在参考轨道坐标系Fo下，航天器P、航天器E以及空间其它目标C与参考质点之间的相对运动方程为

式中：ρi1=[xi，yi，zi]T表示坐标系Fo下航天器i与参考质点的相对位置矢量，其中i={P，E}；ρi2=[vxi，vyi，vzi]T表示坐标系Fo下航天器i的相对速度矢量；fi=-μri/r3i+μrR/r3R，rR=[0，0，-rR]T，rR表示参考质点的轨道半径，ri=为地球引力常数；ui=[uxi，uyi，uzi]T表示航天器i的控制输入；A1=-[ωR×]2；A2=-2ωR×；ωR×表示向量ωR=[0，-θ˙，0]T的反对称矩阵˙表示参考质点轨道角速度。

定义ρPE1=ρP1-ρE1和ρPE2=ρP2-ρE2表示航天器P和航天器E之间的相对位置矢量和相对速度矢量，根据式（1）和式（2）可得航天器P和航天器E之间的相对运动关系方程为

式中：ρPE1=[x，y，z]T；ρPE2==[vx，vy，vz]T；fPE=fP-fE=-μrP/r3P+μrE/r3E。

注释1航天器C泛指空间其他目标，不具有主动碰撞意图，航天器P在对航天器E自主绕飞过程中与航天器C之间的碰撞风险是随机突发事件。航天器P在碰撞威胁规避过程中与航天器C之间的相对运动与式（3）类似，这里不做详细说明，用ρPC和ρ˙PC表示两者之间的相对距离和速度。

根据式（3）可以看出航天器P和航天器E之间的相对运动受航天器P和航天器E的控制策略共同影响，由于航天器E是非合作目标，uE是未知的，因此具有博弈性质，相对运动关系的可控性和稳定性未知。此外，空间其它目标的轨道运动与航天器P的轨道运动存在交会，可能存在碰撞风险，航天器P要较好地实现绕飞任务且保障自身安全性，需要根据与空间目标的相对运动关系自主决策改变行为状态，并根据对应行为状态，建立控制任务目标设并计合适的控制策略使得系统满足指标要求。

分析各个行为状态下对相对运动关系的需求，建立相应行为状态控制目标如下所示。

1）远程接近状态

远程接近状态是指通过制导接近目标，使得与目标之间的相对距离满足期望要求，即

式中：d为与目标实际相对距离；||ρPE1||=为近程接近开始的期望相对距离；ε为允许的误差范围。

2）近程接近状态

近程接近状态是指通过高精度制导使得航天器P到达期望的绕飞位置，即

式中：ρn，ref为期望绕飞位置，ρn，ref满足||ρn，ref||＜d0，ref。

3）相对位置保持状态

相对位置保持状态的目的主要是航天器P用于状态调整或者在有利位置对航天器E进行成像观测，这个状态下要求航天器P与航天器E之间的相对位置保持稳定［14］，即

式中：ρPE1，k表示某一固定相对位置。

4）绕飞转移状态

绕飞转移是为能够对非合作目标进行多方位观测，更好的认知目标，一般为共面绕飞，即要求航天器P与航天器E始终共面。为了保障航天器P与航天器E共面，如图4所示，需要对绕飞轨迹进行规划，使得绕飞轨迹与航天器E共面，然后设计控制策略使得航天器P跟踪参考轨迹即可实现航天器P对航天器E的共面绕飞［15］。

图4 绕飞轨迹Fig.4 Track of fly-around

假设绕飞半径为r，绕飞轨迹所处的平面为W，根据几何关系可知，绕飞轨迹为平面与半径为r的球面与平面W的交线，即

式中：a、b和c为已知实数，可根实际情况进行选择。

根据绕飞任务要求，求解式（7）即可得到绕飞轨迹曲线参数ρr，ref和ρ˙r，ref。绕飞转移过程实际就是跟踪参考轨迹曲线过程，即

式中：表示期望轨迹跟踪速度。

5）碰撞规避状态

在碰撞规避状态，航天器的目标主要是进行碰撞威胁规避控制。设航天器之间安全距离为ds，航天器之间的碰撞预警距离为dc，当两者之间距离为||ρPi1||≤dc(i={E，C})，且1/||ρPi1||＞0时存在碰撞威胁，此时航天器需要改变行为状态，通过控制使得与目标之间保持在安全距离［16］，即

式中：ρPi1表示与航天器E以及其他空间目标C之间的相对位置；εs为允许误差。

6）撤离状态

撤离状态的目的是当航天器结束绕飞任务后，使其能够返回至既定的目标轨道，即

式中：ρc，ref、和分别表示参考轨道坐标系下既定目标轨道位置、轨道速度及轨道加速度。

注释2在对目标观测过程中，考虑到光学载荷对目标观测受到与目标是否逆光的条件影响，只有处于与目标的非逆光条件下才能对目标进行有效观测，因此对目标进行绕飞观测时，选取的观测点需要满足非逆光条件，即

式中：θ=2π/3，表示ρPE1与太阳光矢量之间的不被允许的逆光角度；εθ表示允许的偏差；s表示地心惯性系下太阳光矢量在参考轨道坐标系下的矢量投影，s=R(φ，φ，ϑ)sg，sg表示太阳光矢量在地心惯性坐标系下的投影；˙(φ，φ，ϑ)=-ωR×R(φ，φ，ϑ)，R(φ，φ，ϑ)表示地心惯性坐标系到轨道坐标系的转移矩阵［17］。此外，考虑到若相邻的2个观测点之间的弧度较小可能无法获取目标的新的观测信息，因此，从一个观测方位绕飞转移到另一个观测方位需要大于一定的弧度。

注释3式（5）、式（6）、式（8）以及式（10）所示的条件仅理论数值上成立，考虑到实际系统存在一定的误差，因此在实际情况下需要考虑允许的误差大小。

1.3 状态转换函数

为了实现对非合作目标绕飞的自主控制，航天器P的状态qh(h=0，1，…，5)之间要能够自主根据相对运动关系进行决策自主进行行为状态转换。因此需要根据定义的状态集合Q={qh}(h=0，1，…，5)，设计相应的状态转换函数Tl(l=0，1，…，5)实现状态qh1与qh2(h1≠h2；h1，h2=0，1，…，5)之间的自主转换。设计Tl为由一系列事件集和状态qh组合构成的逻辑函数。

定义事件集E={ej}(j=1，2，…，8)，其中e1表示绕飞任务；e2表示远程接近；e3表示近程接近，e4表示相对位置保持；e5表示目标观测；e6表示碰撞威胁规避；e7表示绕飞转移；e8表示撤离；ej=1或者ej=0(j=1，2，…，8)表示事件的发生或者结束（未发生）。为了实现事件的自主触发，根据1.2节当中的各个行为状态下的控制目标设计事件ei的触发条件如表1所示。

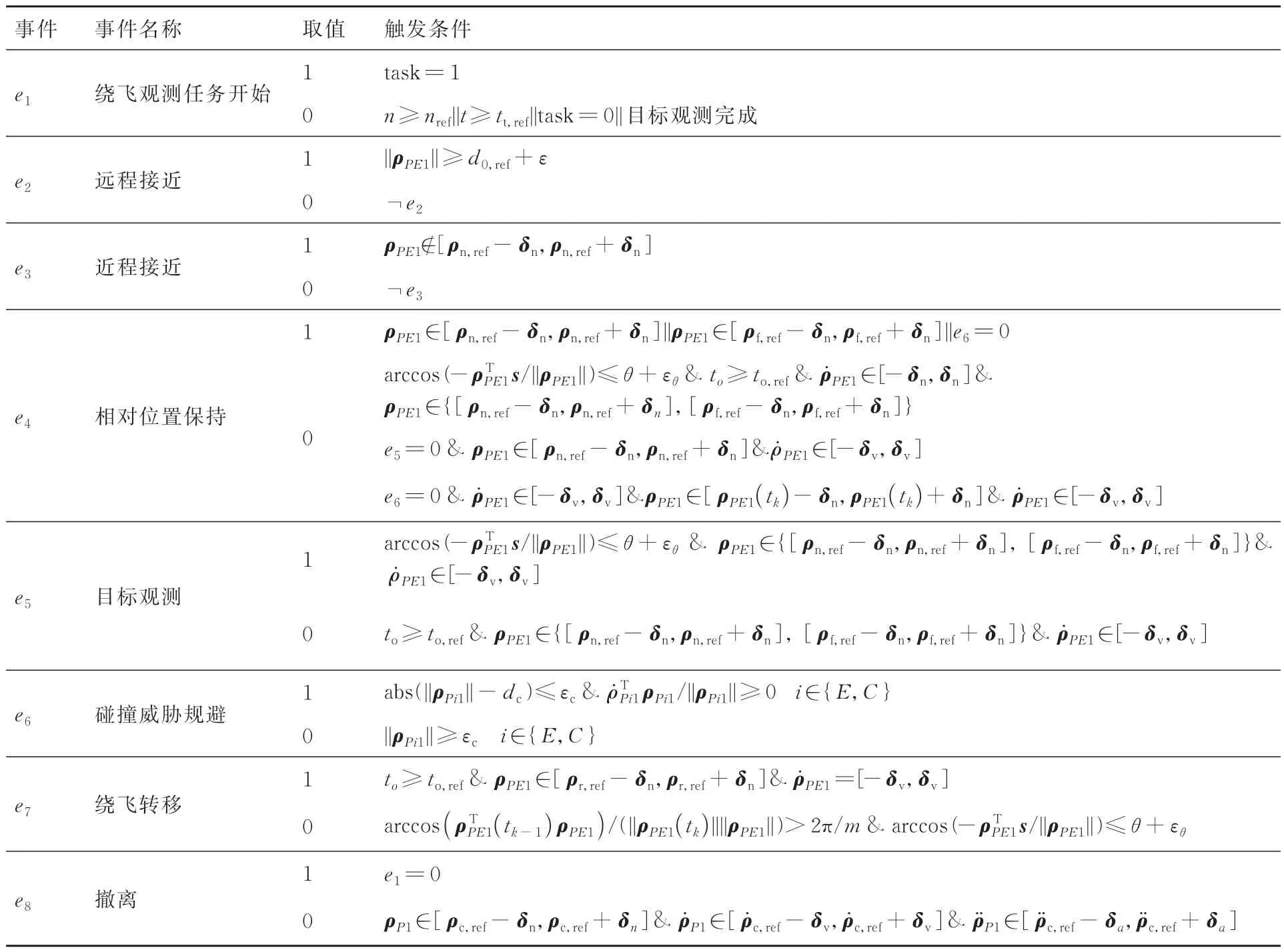
表1 事件集合及触发条件Table 1 Event collection and triggered condition

注释4表1中n表示绕飞圈数；nref表示期望的绕飞圈数；t表示绕飞花费的总时长，tt，ref表示绕飞任务期望的总时长；to表示某一观测方位上花费的观测时长；to，ref表示某一观测方位上期望的观测时长。

注释5ρn，ref表示近程接近过程中的期望绕飞位置，ρf，ref表示绕飞转移过程中arccos(ρTPE1(tk-1)ρPE1/(||ρPE1(tk-1)||||ρPE1||))＞2π/m&arccos(-ρTPE1s/||ρPE1||)≤θ+εθ满足时的位置；ρPE1(tk-1)表示上一次观测目标的相对位置，ρPE1(tk)表示e6=0条件满足时的航天器与绕飞目标的相对位置，只在q4状态下检测事件e6作为事件e4的判断条件。

注释6ε、εc和εθ表示允许的偏差；δn、δv和δa表示相对位置、速度和加速度允许的偏差向量。

注释7绕飞转移结束，即e7=0表示航天器从上一个满足对目标观测条件的方位到现在的满足对目标观测条件的方位已经绕飞转移至少超过2π/m，m为正整数，根据实际情况设计。

注释8事件ej(j=1，2，…，8)当中部分事件属于全局事件，部分事件属于局部事件，全局事件在所有行为状态下都会被检测，局部事件只有在特定的行为状态下才会被检测，其中e1、e4、e6和e8为全局事件，e2、e3、e5和e7为局部事件。

注释9表1为事件发生和结束的条件，并不决定航天器的行为状态转换，相应的事件信息需要反馈到行为状态监控与管理模块，根据航天器的当前行为状态以及状态转换函来决定航天器的行为状态是否发生改变，行为状态转换函数具体见表2。

表2 状态转换及转换函数Table 2 State transition and transition functions

根据设计的事件触发条件，为了协调系统运行，保障绕飞任务的完成和航天器自身的安全性，设计行为状态qh1到qh2(h1≠h2；h1，h2=0，1，…，5)之间的转换函数，具体如表2所示。

通过逻辑分析可知，各状态转换函数之间为互斥的，即各个状态转换函数不存在同时为真的情况，不存在冲突，逻辑是自洽的，能够保证系统的协调。

注释10空间环境的不确定导致航天器任务的执行不确定性，通过建立状态机模型用于对航天器的行为状态监控和管理，使得航天器能够自适应改变自身的行为状态，更加自主的应对空间环境和任务的不确定性。状态转换函数是状态机的重要组成部分，决定状态机的各个状态之间的跳转。状态转换函数是由航天器的行为状态和一系列事件串构成的逻辑函数，状态转换函数的设计要避免相互之间的逻辑冲突，要保障状态机的有序和有向运行。

注释11航天器的行为状态转换是由航天器当前的行为状态和当前发生的事件串来决定的，只有特定的行为状态下特定的事件串为真的情况才会改变航天器的行为状态，使其进入下一个对应的行为状态，其它情况下，则维持当前状态不改变，即使该事件发生也不会改变航天器的行为状态，例如从远程接近状态进入近程接近状态后，假设此时事件e2=1，它并不会让航天器由近程接近状态跳转为远程接近状态，不会在这两个状态之间来回切换，因为在近程接近状态下没有状态转换函数使得航天器可以跳转到远程接近状态。

根据1.1节～1.3节的描述，自主绕飞控制系统的混杂模型可以用如下所示的混合状态机模型进行描述［18-19］。

式中：Q={qh}(h=0，1，…，5)表示有限状态集合；X={ρPE1，}表示连续变量；E={ej}(j=1，2，…，8)表示离散事件集合；U={uph(t)}表示连续动态系统分段控制策略；T={Tl}(l=0，1，2，…，5)表示状态转换函数；Y、f、Init和Inv分别为连续动态系统输出变量集合、连续动态系统微分方程、系统初始值和连续变量约束边界。

2 控制策略设计

考虑到自主绕飞过程中各个行为状态下的控制目标不一样，因此控制策略需要根据实时控制目标进行自主调整。本节要解决的问题是针对各个行为状态下的控制目标设计自主绕飞控制策略设计使得各个行为状态之间的转换过程中，系统动态性能指标是满足设计要求。整个混杂系统的控制结构如图5所示。

图5 混杂系统闭环结构Fig.5 Structure of closed-loop hybrid systems

注释12从图5可知，相比较于传统的航天器控制系统框架，本文提出的控制系统框架，采用分层控制的思想，顶层为离散事件控制系统，监控、规划和管理航天器的行为状态，底层为传统的航天器控制系统，用于轨道控制，反馈信息也由单一的轨道信息变为事件信息和轨道信息，具有创新性。

2.1 运动规划

由于不同行为状态下的控制目标不同，因而采取的控制策略也不相同，为了降低在控制策略切换的过程对控制系统动态性能的影响，对部分状态的运动需要进行规划，给出参考轨迹曲线。

1）q0远程接近状态下的运动规划

在距离目标较远的情况下，为了更加灵活的接近目标，采用基于C-W方程的势函数运动规划方法给出期望运动曲线。假设航天器P与非合作目标航天器E的期望相对运动C-W方程为

式中：ρhPE1，ref和ρhPE2，ref分别表示期望相对运动轨迹和相对速度；uref表示期望控制输入。

构造势函数为

期望控制输入设计为

式中：κ＞0为正常数，从而得到远程接近参考运动轨迹。

2）q1近程接近状态下的运动规划

为了能够更好地到达期望绕飞位置并调整状态，采用多项式运动规划方法给出期望曲线。在不考虑碰撞威胁规避情况下，假设上一个状态为qh1，下一个状态为qh2，h1∈{0，2}，h2∈{2}。假设在状态qh1的终止时刻与目标的相对位置、速度和加速度信息分别为，状态qh3的初始时刻与目标的相对位置、速度和加速度信息分别为的控制目标），则给定规划时长t，可采用五次多项式给出状态qh下的运动规划，具体形式为

式中：b0、b1、b2、b3、b4和b5为参数矢量。

初始时刻约束条件为上一状态qh1的终止时刻相对位置、速度和加速度信息，即

终止时刻约束条件为下一状态qh2的初始时刻相对位置、速度和加速度信息，即

最终通过解式（19）～式（22）方程可求得相关参数为

式中：

最终给出航天器近程接近状态的运动参考轨迹。

在撤离状态q5下，航天器P返回到既定的轨道上，在不考虑碰撞威胁规避情况下，其运动规划采用多项式运动规划方法给出期望曲线。其初始时刻相对运动参数为上一个状态的终止时刻相对位置、速度和加速度信息，终止时刻相对运动参数为ρc，ref、、，然后根据式（23）和式（24）可得相应的参数。

3）q4碰撞威胁规避状态下的运动规划

考虑到任务过程中航天器的安全性问题，航天器在自主绕飞过程中需要与绕飞目标以及其他空间目标之间保持安全距离，当碰撞威胁规避预警事件发生时，航天器进入威胁规避状态，需要进行重规划，以确保对碰撞威胁的规避，保障航天器的安全运行。在进行威胁规避状态下，重规划的初时时刻相对位置、速度和加速度信息为当前状态qh的相对位置ρPi1、速度ρ˙Pi1和加速度ρ¨Pi1（i表示第i个其他空间目标），终止时刻的相对位置、速度和加速度信息为相对位置保持状态q2的初始时刻相对位置ρPik、速度0和加速度信息0。重规划也采用C-W方程的势函数规划方法，构造如下势函数：

式中：n表示碰撞威胁目标的数量；Us表示总势能函数；Uia和Uir分别表示与第i个目标之间的引力势能函数和斥力势能函数；n表示碰撞威胁预警空间目标总数；η1表示吸引力因子，η2表示斥力因子。

在碰撞威胁规避状态，参考期望控制输入为

式中：ρPi1和ρPi2分别表示与空间第i个目标之间的相对距离和速度，从而得到期望相对运动轨迹。

注释13在q2相对位置保持和q3绕飞转移状态下，相对运动状态为既定的，不需要进行相对运动规划。

注释14在远程接近状态和碰撞威胁规避状态，考虑到目标的行为不确定性，采用基于模型的势函数规划方法能够更好的克服不确定性影响，而对于近程接近状态和撤离状态，由于信息精确已知，采用多项式规划能够取得更符合预期的结果。

注释15与传统的基于势函数的规划方法相比较，本文提出的基于模型的势函数规划方法，结合了航天器的任务目标和碰撞威胁规避目标来建立相关势函数，具有创新性。

注释16由于碰撞威胁规避事件是不确定的，其可能在任意状态qh(h≠4)下发生，导致当前任务状态中断。在没有碰撞威胁规避事件情况下，只需进行一次规划，在发生碰撞威胁规避事件后，需要根据当前行为状态以及下一个行为状态的既定控制目标进行重规划，给出新的参考运动轨迹。

2.2 控制器设计

在规划给出的参考轨迹后，需要设计自适应跟踪控制策略保障控制目标的实现。考虑到非合作目标的机动策略未知以及其它不确定性项，星上通过相对导航系统可以测量目标的相对距离和速度，根据式（3）可构造如下降阶非线性观测器对相关不确定参数进行估计。定义f=fPE-uE=[fx，fy，fz]T，降阶非线性观测器设计如下为

定理1给定参数σ1＞0，σ2＞0使得式（32）成立，则观测器式（31）是有限时间收敛的，即limt→tke2=0，limt→tkef=0，其中tk为收敛时间，ef=^-f。

式中：α＞0满足≤α。

证明定义估计误差e2，η=β^η-vη，η={x，y，z}和ef，η=f^η-fη，根据式（3）和式（31）可得

定义ξ=[ξ1，ξ2]T，其中ξ1=|e2，η|1/2·sign(e2，η)和ξ2=ef，η，对ξ1和ξ2求导，根据式（33）可得

选择Lyapunov函数为

对式（35）求导，根据式（34）可得

选择σ1＞0和σ2＞0使得矩阵Σ正定，假设λmin＞0为矩阵Σ的最小特征值，那么式（36）可以写成：

根据规划器给出的运动规划结果以及观测器给出的对于不确定性参数的估计，设计自适应跟踪控制策略实现不同行为状态下的控制目标。考虑到不同行为状态下，控制目标和控制对象发生变化，因此航天器控制器设计为多模态的以适应不同行为状态下对参考轨迹的跟踪，整个连续变量闭环控制系统框架如图6所示。

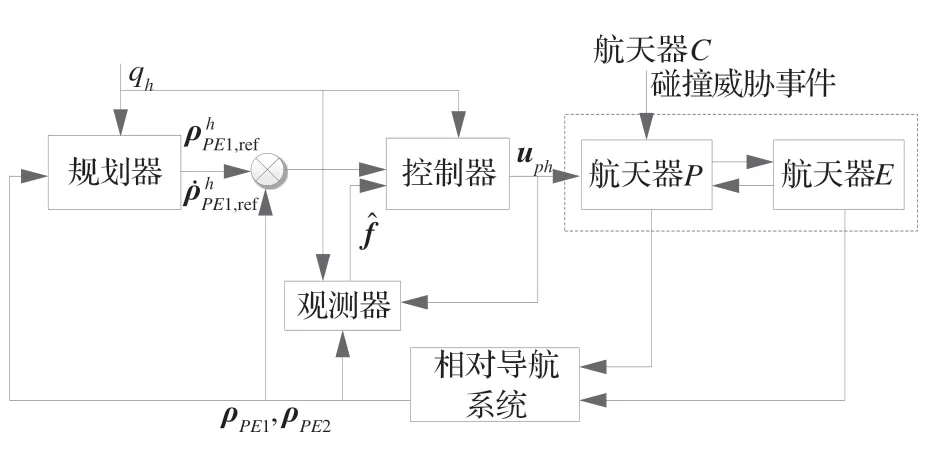
图6 连续变量闭环控制系统Fig.6 Continuous variable close-loop control system

假设状态qh(h∈{0，1，…，5})下规划器给出的参考轨迹为，本文设计一种新型的多模态有限时间收敛自适应跟踪控制器为如下形式：

式中：k1，h＞0和k2，h＞0为正常数，h∈{0，1，2，…，5}表示控制器模态，对应航天器的行为状态；在h∈{0，1，2，3，4}情况下，在h=5的情况下式（38）中^项用于补偿系统中不确定性f额影响，项用于补偿跟踪误差，项用于保证系统渐进收敛，用于加速跟踪误差收敛速度。

根据系统动力学模型可知，跟踪误差动力学方程为

定理2对于误差动力学系统式（39），在控制器式（38）的作用下，其是渐进收敛的，即成立。

证明构建如下Lyapunov函数：

对式（40）求导，可得

将uph代入到上式，因为limt→tkef=0可得

根据式（42）可知，当eh，ref+≠0时，＜0成立，因此误差最终会在有限时间内收敛到-eh，ref，从而可知从而进一步有，即系统是渐近收敛的。证毕。

3 仿真验证

本节通过数值仿真验证本文提出的算法的有效性。具体仿真参数设置为［20］：参考质点轨道半轴长为3×104km，偏心率为0，轨道倾角为π/6 rad，升交点赤经为π/4 rad，近地点辐角为0°，真近点角为0°。航天器P与参考质点之间的相对运动参数初始值为ρP(0)=[200，200，200]T×航天器E与参考质点之间的相对运动参数初始值为：ρE(0)=[0，0，0]T×103km，ρ˙E(0)=[0，0，0]T×103km/s。航天器P的近程接近期望距离为d0，ref=100×103km，航天器P的绕飞平面参数设定为a=1，b=1和c=-(ax+by)/z；绕飞期望位置ρn，ref为航天器P与E相对位置与绕飞曲线的交点，期望绕飞圈数为nref=1；航天器P的期望绕飞半径为R=40×103km；航天器P的碰撞威胁告警距离为dc=30×103km。航天器P的碰撞威胁告警解除距离为ds=50×103km。太阳光矢量方向初始值为s0=[1，0，0]。降阶观测器参数选择为状态q0、q2和q3：σ1=0.3，σ2=0.05；状态q1和q5：σ1=0.2，σ2=0.03；状态q4：σ1=0.5，σ2=0.05。控制参数设计为状态q0：k1，h=0.005，k2，h=0.002；状态q1、q2、q3和q5：k1，h=0.05，k2，h=0.01；状态q4：k1，h=0.035，k2，h=0.01。仿真结果如图7～图24所示。

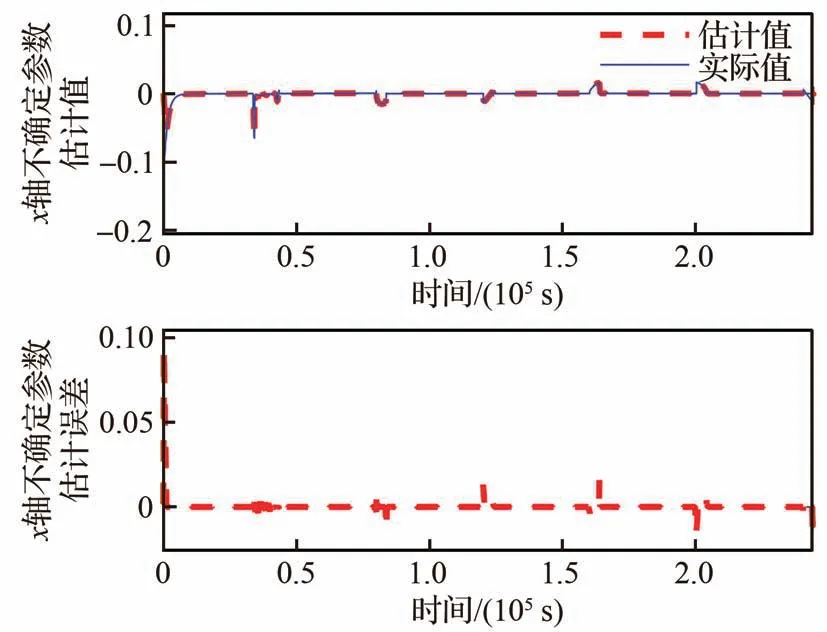
图7 不确定参数fx估计值及误差Fig.7 Estimation and estimation error of uncertainty fx

图8 不确定参数fy估计值及误差Fig.8 Estimation and estimation error of uncertainty fy

图7～图9为不确定参数f(t)=[fx(t)，fy(t)，fz(t)]T的三轴估计曲线及估计误差曲线，图10～图12为状态q0～q4下，航天器P和航天器E之间的三轴相对运动变化曲线及跟踪误差曲线，图13～图15为航天器P与既定返回目标轨道位置之间的三轴相对位置变化曲线及跟踪误差曲线。图16为航天器P的事件活动图；图17为航天器P的状态转换图；图18为航天器P与E之间的相对位置与太阳光矢量之间的夹角；图19为航天器P与E以及C之间的相对距离变化曲线；图20为状态q0～q4下，航天器P和E之间三维空间坐标下的相对天器P的运动曲线图；图21～图23为三轴控制器输出；图24为正常情况和碰撞威胁规避情况下，航天器之间的相对运动曲线比较。

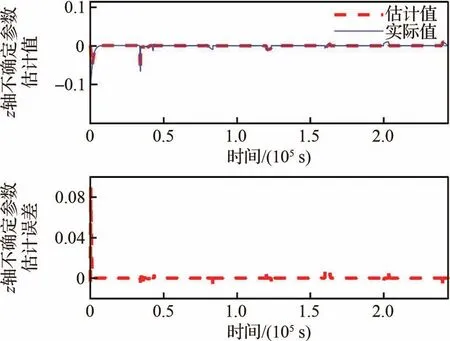
图9 不确定参数fz估计值及误差Fig.9 Estimation and estimation error of uncertainty fz

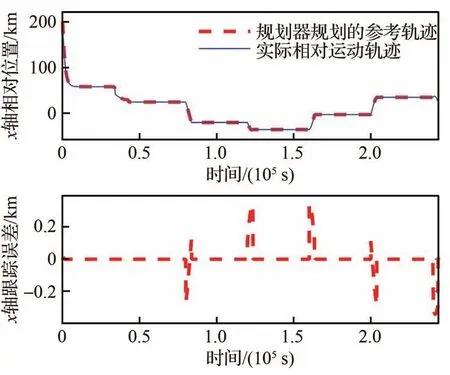
图10 x轴相对位置及跟踪误差曲线Fig.10 Relative motion and tracking error of x axis

图11 y轴相对位置及跟踪误差曲线Fig.11 Relative and tracking error motion of y axis

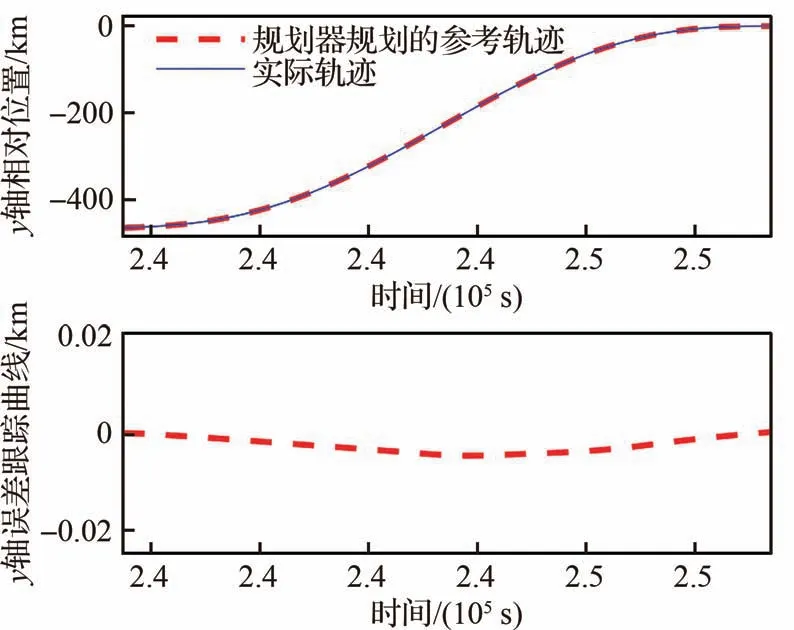
图14 航天器P与返回轨道的y轴相对位置Fig.14 Relative position of y axis between spacecraft P and return trajectory

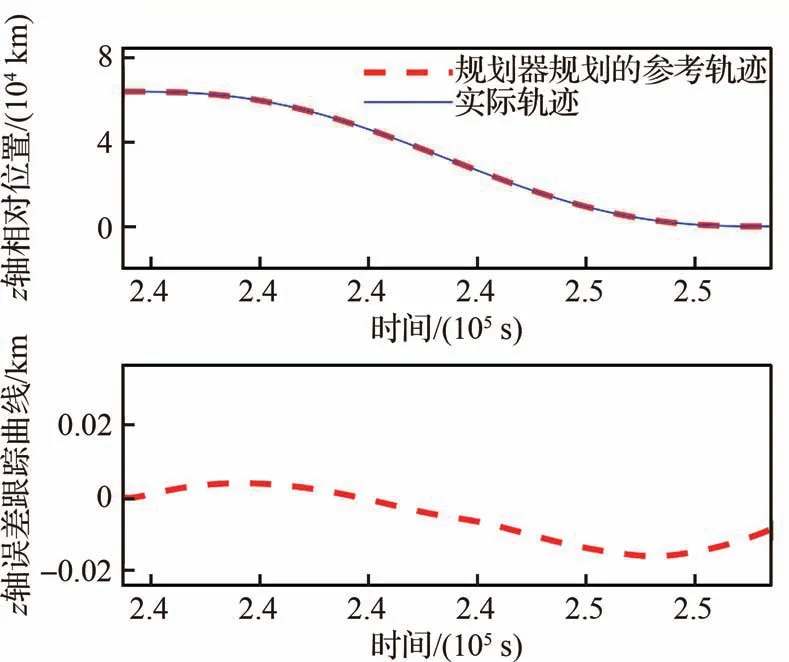
图15 航天器P与返回轨道z轴相对位置Fig.15 Relative position z axis between spacecraft P and return trajectory

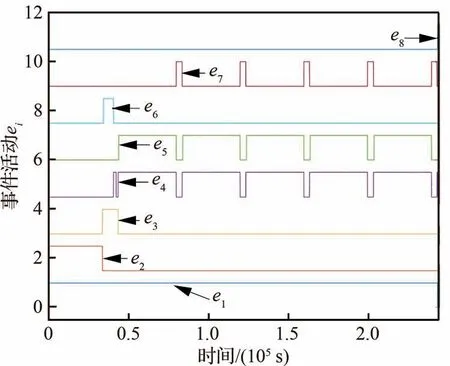
图16 航天器P的事件活动Fig.16 Event activity of Spacecraft P

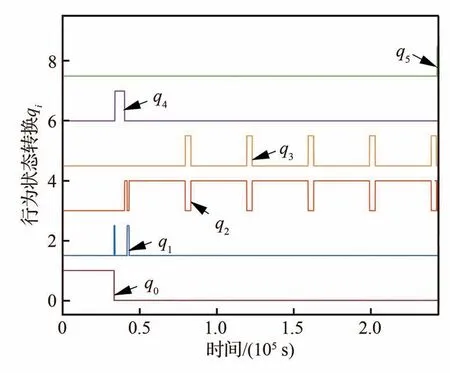
图17 航天器P的状态转换Fig.17 State transition of Spacecraft P

图18 相对位置矢量与太阳光矢量之间的夹角Fig.18 Angle of relative position vector and sunlight Vector

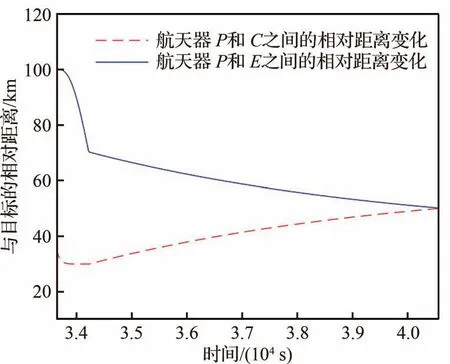
图19 航天器之间的相对距离Fig.19 Relative distance of spacecrafts

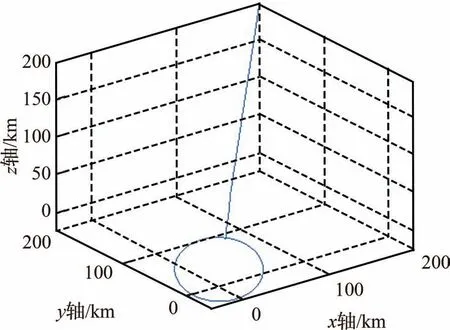
图20 航天器P与航天器E之间的相对运动三维视图Fig.20 3D view of relative motion between Spacecraft P and Spacecraft E

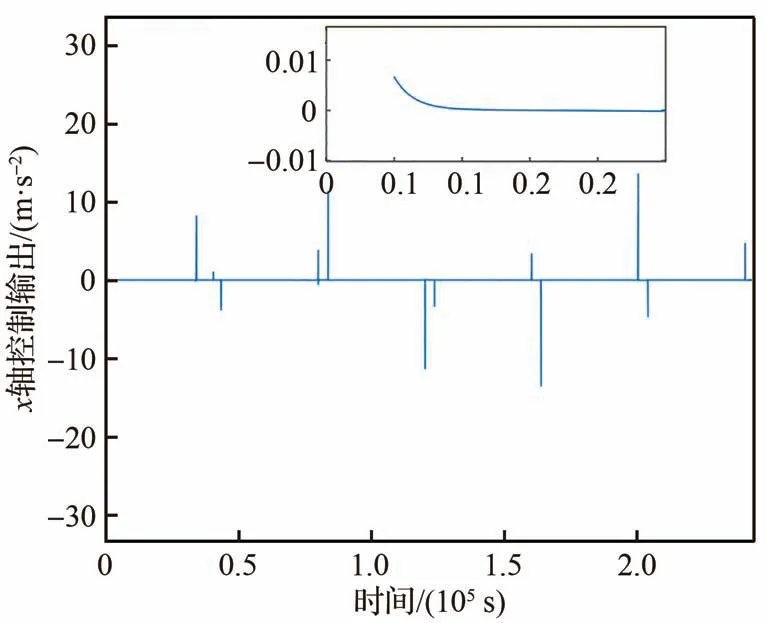
图21 x轴控制输出Fig.21 Control output of x axis

图22 y轴控制输出Fig.22 Control output of y axis

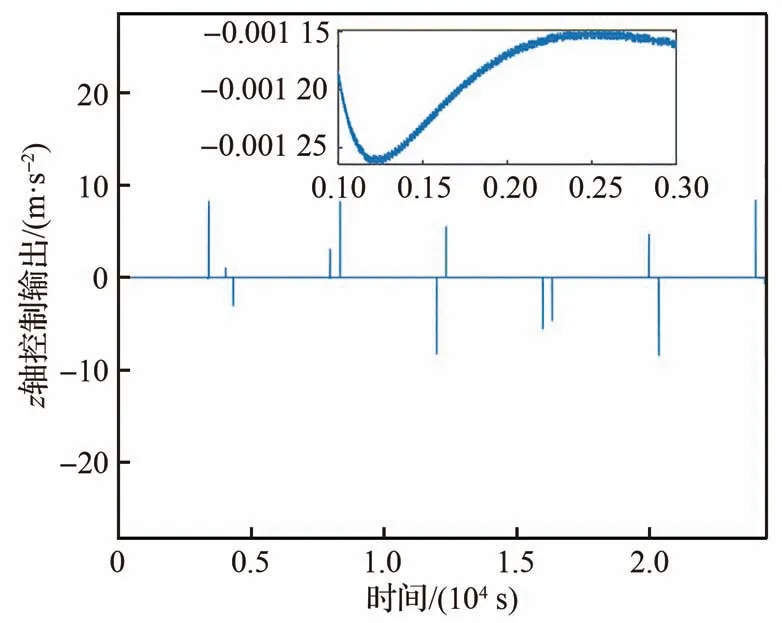
图23 z轴控制输出Fig.23 Control output of z axis

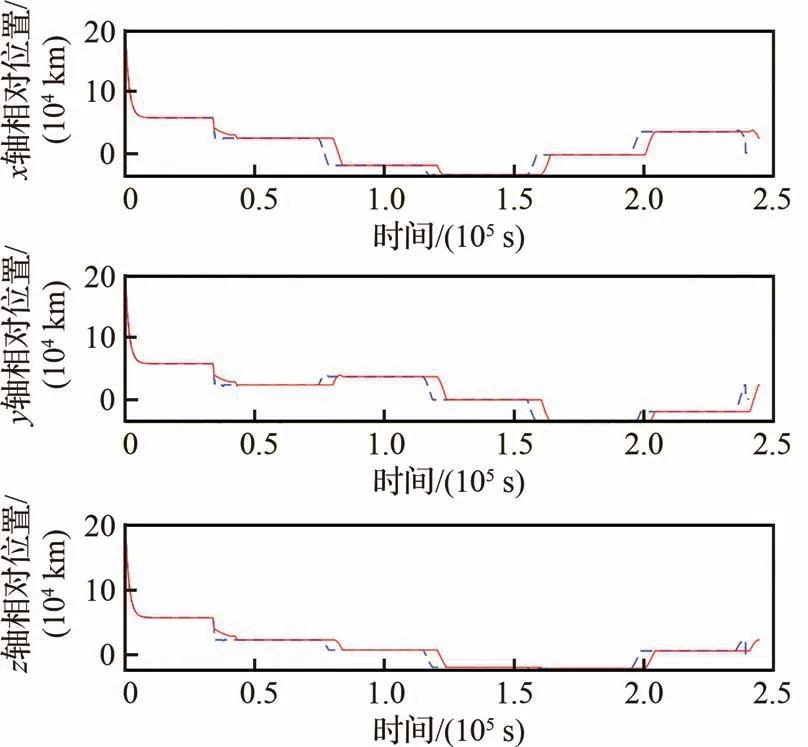
图24 正常情况和碰撞威胁规避情况轨迹Fig.24 Trajectories of normal and collision threat avoidance case

根据图7～图9可知，所设计的观测器能够有效估计包含非合作目标未知机动参数在内的不确定性估计。根据图10、图13和图15可知，所设计的控制策略能够有效跟踪规划器规划出来的参考轨迹（红色为规划器输出参考相对运动轨迹，蓝色为实际相对运动轨迹），说明设计的多模态自适应控制器是有效的。图16～图17中纵坐标是无单位的，事件ej(j=1，2，…，8)和状态qh(h=0，1，…，5)的取值都是0和1，这里为了方便看清楚事件活动和状态行为的转换，将每个事件的纵坐标分别进行了一定的平移。根据图16和图17可知，航天器P的行为状态转换能够主动根据事件触发其转换，整个过程的转换关系为q0→q1→q4→q2→q1→q2→q3→q2→q3→…→q2→q5，与设计的状态转换函数关系分析对应一致，说明设计状态转换函数是可靠的，能够实现航天器的行为协调控制。

根据图17和图19可知，在碰撞威胁规避事件发生后，航天器P能够进入威胁规避状态，对运动轨迹进行重规划，实现对空间目标碰撞威胁规避，在完成对空间目标碰撞威胁规避后，进入相对位置保持状态，重新调整规划接近目标。图18为航天器P在对航天器E绕飞过程中，相对位置矢量与太阳光矢量之间的夹角变化，设当夹角＞5π/6 rad时视为逆光，不利于对航天器E的观测。根据图20可知，在整个绕飞过程，航天器P能够在规避威胁的同时实现对航天器E的接近绕飞详查，实现既定任务的同时保障自身安全。

根据图21～图23可知，航天器的控制输出在对应的行为状态下是连续的，只有当航天器的行为状态发生改变时，其才会发生较大变化。图24展示了正常（即没有碰撞威胁目标时）和碰撞威胁规避2种情况下，航天器的运动轨迹，从图中可以看出，相比较正常情况下，航天器的运动轨迹在碰撞威胁事件发生后，进行了重规划，运动轨迹与正常情况下发生了一定的偏离，同时由于要对碰撞威胁进行规避，整个绕飞过程花费的时间也稍微多于正常情况。

通过仿真验证，本文提出的航天器自主绕飞与威胁规避控制方法能够根据触发事件，通过有限状态机进行协调管理，实现系统行为的协调，自主根据触发事件改变行为状态，规划自身的安全运动轨迹，并通过所设计的自适应控制策略实现对参考轨迹的高精度跟踪，具备在完成控制目标任务的同时实现对空间碰撞威胁的规避的能力。本文所提出的自主控制方法使得航天器具备自主实现更加复杂任务的能力，模型具有可解释性，所设计的多模态控制器能够从理论上分析其可靠性和安全性，为航天器智能自主控制提供一种设计思路。