“新定义”巧创设,新高考妙创新

⦿ 陕西省延安市实验中学 郝变军

创新意识与创新应用是新时代的主旋律,也是高中数学教学与学习中需要不断渗透与培养的一种基本精神与能力.借助“新定义”,可以巧妙进行数学知识中的概念类比、公式设置、性质应用、知识拓展与创新应用等的交汇与融合,很好地融入创新意识与创新应用,成为高中数学试题命制与创新中的一道亮丽风景线,合理情境创设,巧妙创新应用.

1 新概念类比

通过新概念的引入与类比等来创新定义,巧妙融入已有数学基础知识中的相关概念,合理类比与转化,实现创新应用.

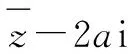
A.第一象限 B.第二象限

C.第三象限 D.第四象限

分析:根据题意,从新概念“等部复数”入手,利用复数的四则运算,结合新概念的内涵构建对应的关系式,进而得以确定对应的参数值,并利用复数的运算与几何意义来深入分析与应用.

解析:依题可得z=(2+ai)i=-a+2i.

结合题中创新概念“等部复数”,可得-a=2,解得a=-2,则z=2+2i.

故选择答案:A.

点评:新概念是新高考创新定义中最为常见的一种类型,通过已有数学知识与对应概念的类比、拓展与深化,构建一个全新的概念,进而结合相关的数学基础知识与数学思想方法等来合理逻辑推理与数学运算等,实现创新应用.

2 新公式设置

通过新公式的设置与应用等来创新定义,巧妙构建一个全新的表达形式或公式,方便数学运算中的运算规则与分析,实现创新应用.

例2〔2023届浙江名校协作体高三(下)开学考试数学试卷〕已知对任意正整数对(h,k),定义函数f(h,k)如下:f(1,j)=1,(i+1)f(i+1,j)=(j-i)·f(i,j),i≤j,则( ).

A.f(i+1,j)=1

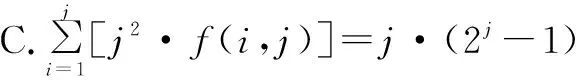
分析:根据创新定义给出相应的新公式,公式的化简与变形是解决问题的关键,这里借助公式的变形,结合组合数公式来转化与应用,并利用递推问题中的累加法或累乘法,实现创新公式问题的解决与判断.

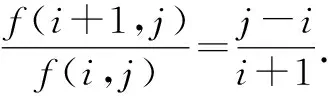
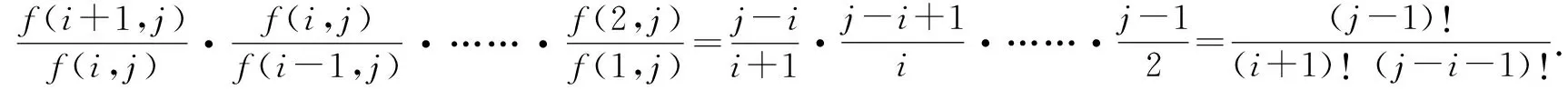
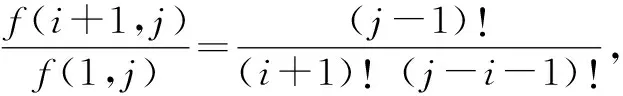
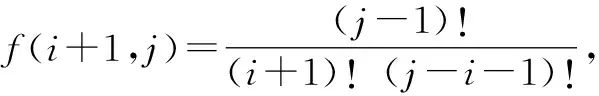
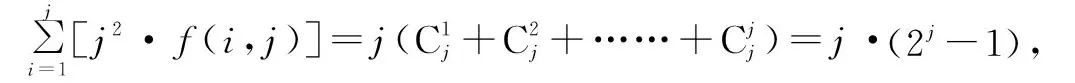
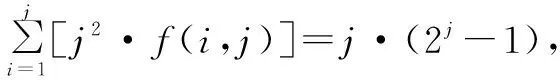
故选择答案:C.

点评:抓住新公式的形式与内涵,合理变形与转化,方便进一步数学运算与逻辑推理.特别可借助一些特殊值代入公式来合理排除与应用,也可以借助一些连续特殊值的分析来寻找规律,并总结基本性质等.

3 新性质应用

通过新性质的给出与应用等来创新定义,借助研究对象的新性质,得到数学运算的对应性质,合理应用与转化,实现创新应用.

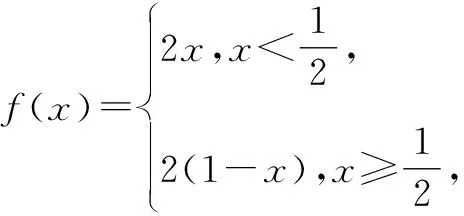
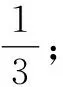
分析:根据题设创新概念,给出函数的新性质,挖掘性质内涵.由函数周期点的创新定义与性质,可得直线y=x与y=f(x)存在交点,对题目中的命题逐一进行分析,结合题意即可得出结论.

对于①,当x0=0时,x1=f(0)=0,周期为1,命题正确;

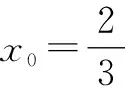
对于④,当x0=1时,x1=f(1)=0≠x0,所以1不是f(x)的周期点.

综上分析,对应各值是f(x)周期为1的周期点的有①③.

故填答案:①③.

点评:结合新性质,回归问题的本质与内涵,利用相关性质的展示与应用来分析与解决问题.寻找新性质与已有数学基础知识之间的共同点与不同点,注意正确区别与联系,合理辨析与应用.

在实际解决“新定义”问题时,关键是正确提取新定义中的新概念、新公式、新性质、新模式等信息,确定新定义的名称或符号、概念、法则等,并进行信息再加工,寻求相近知识点,明确它们的共同点和不同点,探求解决方法,在此基础上进行知识转换,有效输出,合理归纳,结合相关的数学技巧与方法来分析与解决.“新定义”问题作为创新应用的一个基本视角,在创新定义的过程中渗透创新意识与创新应用,有效检测学生对知识理解与掌握的广度和深度,挖掘学生的学习潜能,提高数学品质,提升数学能力,培养创新意识与数学核心素养.