深度学习视域下“平面向量的概念”教学设计
2023-10-16哈尔滨师范大学教师教育学院周文静
⦿ 哈尔滨师范大学教师教育学院 周文静
“平面向量”这样既具有代数特征又具有几何特征的概念是学生在以前的学习中没有接触过的.学生对平面向量的学习往往流于表面,没有掌握其本质,因此需要利用深度学习理论,对“平面向量的概念”的课堂教学进行重构.
1 核心概念界定
深度学习是指在教师的引领下,学生对所学习的课题进行深度探索,挖掘数学概念本质,深度理解概念并内化概念,掌握概念的过程.学生通过深度学习后,体会概念生成的路径,学会挖掘数学概念的数学思想方法.概念深度学习是否发生,主要看是否具备以下几个特征:一是联想与建构,把新知与旧知联系起来,在建构主义学习理论的支撑下,建立自己的知识体系;二是活动与体验,学生亲自经历数学概念的产生,探索概念的生成过程,形成科学的思维方式;三是本质与变式,能够抓住教学内容的关键特征,全面把握学科知识的本质联系,在变式中辨析本质特征[1].
2 “平面向量的概念”教学设计
2.1 联系生活实际,激发探究兴趣
通过生活中的具体情境,降低学生对新授课的恐惧心理,体会数学来源于现实生活,与现实生活紧密联系,从而提高学生积极探索数学概念的兴趣.
教学片段一:创设情境,联系生活实际
问题1如图1所示,猫能捉到老鼠吗?

图1
问题2如图2所示,物体在地面上受到重力,重力的方向是怎样的?重力的大小与什么有关?

图2
如图3所示,物体在液面上受到浮力,浮力的方向是怎样的?浮力的大小与什么有关?
图3
设计意图:向量的概念有着丰富的实际背景.通过生活中有趣的“猫捉老鼠”情境,激发学生的学习兴趣;通过重力与浮力的大小与方向,引导学生感受向量的物理背景,引出向量的两个关键元素——大小和方向,自然引出本节课的探究内容.
2.2 小组交流探究,体验概念生成
“经验是永久的生活老师”,只有体会概念的形成过程,才能深入掌握数学概念的本质.教师层层设问,小组交流,学生挖掘概念.通过自己探索总结出的概念,才能真正将其内化,从而形成合理的认知结构[2].
教学片段二:层层设问,助力概念形成
问题3小组合作交流,讨论质量、位移、力与速度这四个物理量的异同,总结这四个物理量的相同点和不同点.
围绕“四有两责”建机制,筑牢基层监管的安全网。着眼“四有”夯实基础。在2013年9月的机构改革中,酒泉市局和各县(市、区)局同步完成组建,如今,酒泉市67个乡镇均设立了食品药品监管所。着眼基层夯实责任。该局全面推行网格化监管,形成了市、县、乡、村四级网格。积极推行“双随机”监督检查,实施食品药品“红黑名单”制度,促进监管责任落实和企业自律。着眼检测强化支撑。市食品检验检测中心在全省率先通过实验室资质认定,各县(市、区)均成立了食品药品检验检测中心,敦煌市被国家总局列入全国第一批区域性检验检测中心建设项目。
追问1:我们从一支笔、一棵树、一本书中,能抽象出数量“1”.类似地,可以对力、位移、速度这些量进行抽象,形成一种新的量——向量.
你能总结出向量的概念吗?
生:既有大小又有方向的量叫做向量.
追问2:向量与数量之间有什么异同?
生:向量既有大小,又有方向;数量只有大小,没有方向.
追问3:物理学中常称向量为矢量,数量为标量,物理中还有什么量是向量?你能举出例子吗?
设计意图:找到数量与向量的不同点,深入理解向量的概念,找到与其他学科知识的联结点,自然地引出向量的几何表示.
问题4数量可以用实数来表示,数轴上的点与实数存在一一对应的关系,所以数量可以用数轴上的点来表示,那么,该如何表示向量呢?在小船航行中,我们用一条“带有方向的线段”来表示小船从A地到B地的位移,那么线段的大小表示什么?箭头的方向表示什么?
生:找到起点,线段AB的长度表示小船位移的大小,线段AB上箭头的方向表示小船位移的方向.
教师活动:给出有向线段的概念与表示方法,并指出可以用有向线段来表示向量.带领学生一起总结如何用有向线段表示向量.
师:除了可以用有向线段的起点与终点字母来表示向量,还可以用小写字母a,b,c来表示,注意书中是用印刷体黑体表示.
设计意图:将“既有大小又有方向的量——向量”从文字语言变成符号语言,体现了数学概念的简明化与符号化特征,感受数形结合的魅力.
2.3 建构概念体系,感受概念本质
数学概念的顺应指出学生需要调节、改变原有的数学认知结构,以便于概括新的数学概念.“平面向量的概念”这节课有很多知识点,对于零散的概念,从核心概念的本质出发,让学生直观感受概念的生成,形成系统的知识体系[3].
教学片段三:概念深化,形成知识体系
问题5对于两个向量a,b,当两个向量方向相同时,如何画出这两个向量?两个向量能否比较大小?
生:向量不能比较大小,因为其方向无法确定.

图4
生:大小相等,方向相同.
师:请给出相等向量的概念.
追问2:表示这两个向量的有向线段起点位置相同吗?
生:不相同,可以用一条有向线段表示两个相等的非零向量.
追问3:与有向线段的起点在哪是否有关?
生:无关,因为向量只有大小和方向两个元素.
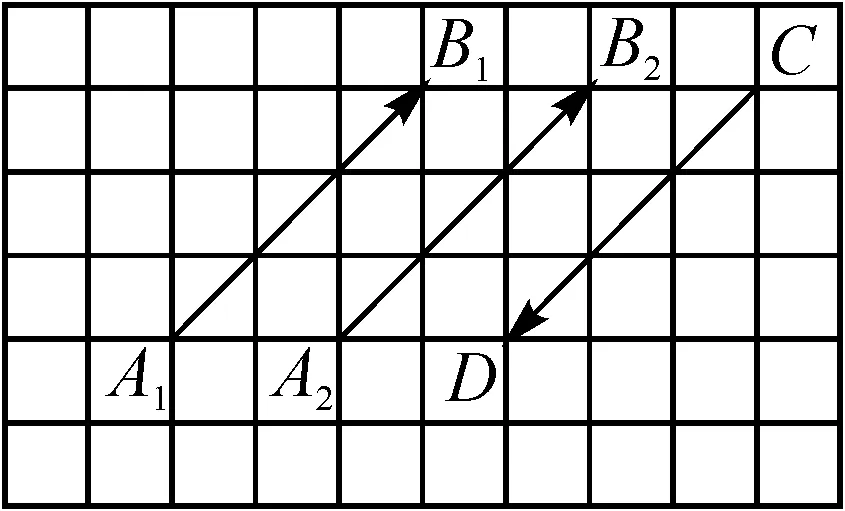
图5
追问5:相等向量和相反向量与平行向量之间有怎样的关系?
生:相等向量和相反向量都是平行向量.
追问6:a,b,c是一组平行向量,在一条与a所在直线平行的直线上,能否作出与a,b,c相等的向量?
追问7:相等向量、相反向量、平行向量与共线向量这四者之间有怎样的关系?
设计意图:学生直观感知平行向量、相反向量、相等向量等概念,并理解平行向量、相反向量、相等向量之间的关系,使概念成为学生观察、比较、抽象、概括后的自然产物.
问题6本节课你收获了哪些知识与方法?
设计意图:课堂小结在教学中起关键作用,师生一起总结课堂上收获到的知识点,不仅仅是为了形成知识体系,更重要的是要让学生掌握概念的生成过程与本质,感受到探究数学概念的路径与数学思想方法.
数学概念课是高中数学的重要组成部分,数学概念在学生高中数学学习中起着关键作用.对数学概念的本质把握不到位,在数学学习中就会出现本质性的错误.很多时候学生在学习数学概念后,只知其然,不知其所以然.在深度学习视域下,通过直观想象探索平面向量的本质,学生对于数学概念的学习从“浅尝辄止”到“入木三分”,能达到“知其然,知其所以然,何由以知其所以然”这三个层次.
