构造与解题齐飞,技能共素养一色

⦿ 安徽省淮南市第二十一中学 杨丹旸

构造法是数学学科中一个非常特殊且优美的解题方法,具有悠久的历史.一些著名的数学家,如欧几里得、欧拉、高斯等人,都有成功借助构造法解决一些数学难题的记载与传说.特别地,随着新高考改革的逐步推进与深入,利用构造法解决数学问题也成为一个创新点与亮点,在高考数学命题、自主招生以及数学竞赛等中都有着非常重要的地位,倍受各方关注.

1 构造函数妙解题

例1〔2023届鄂东南省级示范教育教学改革联盟学校高三(上)期中数学试卷〕已知a=e-2,b=1-ln 2,c=ee-e2,则( ).

A.c>b>aB.a>b>c

C.a>c>bD.c>a>b

分析:根据题设条件,以三个代数式的大小比较为具体情境,通过分析代数式的结构特征,寻觅函数与不等式之间的结构特点与共性,进而巧妙构造与之相关的函数模型,结合函数的单调性及不等式的基本性质来分析与判断.

解析:构造函数f(x)=ex-x,x>0,则f′(x)=ex-1>0,于是函数f(x)在(0,+∞)上单调递增.

所以f(e)>f(2),即ee-e>e2-2,亦即ee-e2>e-2,故c>a.

又f(1)>f(ln 2),即e1-1>eln 2-ln 2,亦即e-1>2-ln 2,于是e-2>1-ln 2,故a>b.

综上分析,可得c>a>b.

故选择答案:D.

点评:遇上指数、对数、幂函数等值的大小比较时,关键是寻找常数和指数、真数等的关系后,合理通过构造函数的方法来分析与解决问题,成为判定代数式的大小关系中比较常用的一种技巧方法,频繁在解题过程中得以巧妙应用,学生应熟练掌握.寻找代数式的关系,合理构造对应的函数,结合导数法以及函数的单调性加以转化与应用.

2 构造方程妙解题

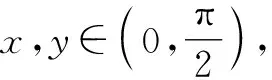
A.8 B.9

C.10 D.其他三个选项均不对

分析:根据题设条件,结合三角代数式的变形与转化,通过放缩消参后,合理进行整体换元处理构造相应的方程.结合常数1=sin2x+cos2x这一基本关系式进行消元处理,转化为相关的二次方程问题,借助判别式法巧妙构建对应的不等式,利用不等式的求解来确定相应的最值问题.

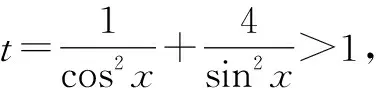
依题知,以上关于sin2x的二次方程有实根,则利用判别式Δ=(t+3)2-16t≥0,整理得t2-10t+9≥0,解得t≥9,或t≤1(舍去).

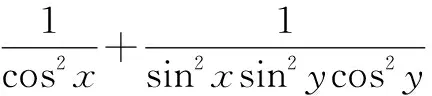
故选择答案:B.

点评:合理联系三角关系式,巧妙放缩,结合换元处理以及方程的构造,利用判别式法将其转化为对应的不等式问题,实现问题的转化与应用.方程的构造对于解决参数值的求解与取值范围的确定,以及代数式的取值范围(或最值)等有奇效,借助方程的求根以及判别式等来综合应用.

3 构造数列妙解题

例3(2023届苏锡常镇四市高三教学情况调研数学试卷)已知数列{an}的前n项和为Sn,a1=1,若对任意正整数n,Sn+1=-3an+1+an+3,Sn+an>(-1)na,则实数a的取值范围是( ).

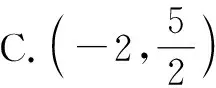
分析:根据题设条件,结合条件中数列递推关系式的结构特征,整体化处理与思维切入,进而巧妙构造新数列,利用新数列的基本知识来分析与解决,进而综合题设中的数列不等式的应用来转化,得以巧妙解决参数的取值范围问题.

解析:构造数列{bn},使得bn=Sn+an,则bn+1=Sn+1+an+1.

结合Sn+1=-3an+1+an+3,可得

Sn+1=-2an+1-(Sn+1-Sn)+an+3.

整理,可得2(Sn+1+an+1)=(Sn+an)+3,即2bn+1=bn+3,亦即2(bn+1-3)=bn-3.

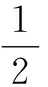
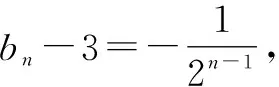
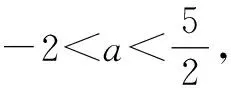
故选择答案:C.

点评:在处理一些复杂的数列问题时,巧妙构造新数列来分析,让人耳目一新,成为解决问题的一种 “巧技妙法”.这里要依据问题中数列递推关系式的结构特征来构造新数列,进而合理变形与转化,实现问题的化归,结合数列的基础知识与相关公式合理构造,优化解题,提升效益.

4 构造图形妙解题

例4〔福建省泉州市2023届高中毕业班质量监测(三)数学试卷(2023年3月)·8〕已知平面向量a,b,c满足|a|=1,b·c=0,a·b=1,a·c=-1,则|b+c|的最小值为( ).

分析:根据题设条件,结合平面向量的几何内涵或对应的几何意义,从“形”的视角切入,通过构造平面几何图形,利用数形结合来加以直观想象,从几何特征层面来研究对应的问题.

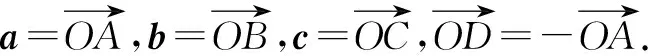
由a·b=1,a·c=-1,b·c=0,结合平面向量数量积的几何意义,可得AB⊥OA,DC⊥DO,OB⊥OC,如图1所示.

图1

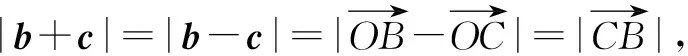
故选择答案:C.

点评:本题合理构造平面几何图形,结合平面向量数量积的几何意义,从射影、垂直等视角来直观处理,利用图形直观,结合“动”态变化规律来解决“静”态的最值问题.构造平面几何图形往往可以解决平面向量、三角函数、解三角形等相关问题,构造平面解析几何图形往往可以解决直线与圆、圆锥曲线等相关问题,构造立体几何图形往往可以解决空间几何体等应用问题.

在实际解决数学问题时,利用构造法巧妙解题与应用没有固定的模式与程序,往往可以从“数”的视角构造函数、方程、数列等代数模型,也可以从“形”的视角构造向量、图形等几何模型,不可生搬硬套.

具体解题时,关键是结合题设条件与所求结论之间的联系,合理构建相应的链接.合理通过数学模型的构造来产生联系,进而构建起“已知”与“所求(所证)”之间的“桥梁”,从而使得问题的解决另辟蹊径,问题的处理水到渠成,在一定程度上有效提升数学能力,强化数学解题技能,培养数学核心素养.