“质疑”与“建模”素养下对“尺缩钟慢”证明的再讨论
2023-10-10谈元凯
谈元凯
(上海市洋泾中学 上海 200122)
陈 辰
(上海市第八中学 上海 200011)
1 前言
2021年9月始,上海在高一年级全面推行了新教材与新课标.其中在沪科版必修二的教学安排中,设计了“相对论初步”这一节.需要学生在学习过高中力学的全部内容后理解牛顿运动定律的局限性,并且还要知道一些关于狭义相对论的初步概念.
结合新课标核心素养的相关要求,教师可以在教学时适当对部分学有余力的学生提出一些较为灵活和高要求的学习方式.这里结合物理核心素养中“质疑”精神和“建模”能力这两大要素[1],对教材中“尺缩钟慢”效应的证明与推导做一个再讨论.
2 教材中“尺缩钟慢”的证明
2.1 “钟慢”效应的证明
在“钟慢”效应的证明方面,教材是这样叙述的[2]:
如图1(a)所示,假设一高铁列车沿直线轨道以匀速v向右运动,车厢地板上一个光源向上发出一个闪光,被车厢顶部的反射镜反射回车厢底板,并用一个钟记录下光脉冲来回运动经历的时间.

(a)

(b)图1 “钟慢”效应分析图
假设车厢高度为h,因为光速为c,所以车厢里观察者看到的时间间隔为
(1)
在地面上的观察者看来,当光脉冲向上传播和返回时,车厢同时在以匀速v向右运动,因此光脉冲的路径是等腰三角形的两条斜边,如图1(b)所示.
如果光脉冲来回的时间间隔是Δt′,则有
消去h后可得
(2)
由于v 故 Δt′>Δt 在“尺缩”效应的证明方面,教材是这样叙述的: 如图2(a)所示,在直杆的一端装上激光发射器和接收器,另一端装上反射镜.当发射器发出激光被反射镜反射回接收器时,记录下激光往返的时间间隔Δt,即可得到直杆的长度为 图2 “尺缩”效应分析图 即 (3) 假设直杆所在的参考系相对地面以匀速v向右运动,如图2(b)所示.如果地面观察者测得的直杆长度为L′,设激光从直杆左端发出到达反射镜的时间为Δt′1,因为在这段时间内直杆向前运动了vΔt′1的距离,因此有 (4) 同理,设激光从反射镜返回接收器的时间间隔为Δt′2,如图2(c)所示.在这段时间内直杆向前运动了vΔt′2的距离,因此有 (5) 因此,地面观察者测得总的时间间隔为 Δt′=Δt′1+Δt′2= (6) 注意到Δt′是地面观测者测得的激光从发出到接收的时间,Δt是相对直杆静止的观测者测得的相应的时间间隔.根据前面讨论的时间的相对性,两者满足关系式(2). 将式(3)、(6)代入式(2)可得 (7) 由于v 故 L′ 通过阅读教材中的证明过程可以发现,在证明“尺缩钟慢”效应的过程中,教材建立的模型都是光线传播的往返过程[2]. 通过思考,可以提出这样的疑问:如果研究光线传播过程中的某一单向过程,能否得出“尺缩钟慢”的相对论效应呢? 在图1(a)中,如果只考虑光线的单向传播过程,车厢里观察者看到光脉冲从发出至射到车厢顶部反射镜的时间间隔为 (8) 图1(b)中,在地面上的观察者看来,当光脉冲传播时,光脉冲从发出至射到车厢顶部反射镜的时间间隔是Δt′,则有 消去h后可得 (9) 可以发现,式(9)与式(2)完全相符.说明无论取光线的单向传播过程还是往返过程,得到的相对论效应的结果是一样的,即:一个静止的观察者会发现匀速运动的参考系中所有过程都变缓了,而在这个参考系中的观察者却认为一切正常. 在图2(a)中,如果发射器发出激光射到反射镜上时所用的时间为Δt,即可得到直杆的长度为L=cΔt,即 (10) 假设在图2(b)中直杆所在的参考系相对地面以匀速v向右运动,地面观察者测得的直杆长度为L′,设激光从直杆左端发出到达反射镜的时间为Δt′,考虑这段时间内直杆向前运动了vΔt′的距离,因此有 (11) 考虑到相对论的时间修正,满足 将式(10)、(11)代入式(2)可得 (12) 综上所述,同样取了光脉冲单向的传播过程,为什么不同的相对论效应做出来的结果是不同的呢?时间修正完全与教材的证明结果一致,但长度修正虽然能定性看出在“缩短”,但是和教材的表达式完全不同. 如图3所示,有两个一维惯性参考系S和S′.其中惯性参考系S沿着x轴以匀速v相对于S′系向右运动.以两个惯性参考系的原点相重合的瞬间作为计时的起点,某时刻有一事件发生在点P,从S系看,P点的位置坐标为x,从S′系看,P点的位置坐标为x′.爱因斯坦从狭义相对论的基本原理出发,导出了在S系中位置坐标的洛伦兹变换[3],满足 图3 洛伦兹坐标变换 实际上,空间中任何物体的长度应该是同一时刻观测到的物体两端点之间的位置坐标之差.所以如果以光的单向传播作为研究过程的话,起点和终点为两个不同的坐标,在相对论效应下观测到的结果都发生了变化,而地面观测者看到的直杆长度其实是两个端点的坐标之差. 所以教材中为了避免两个坐标都发生变化引起的偏差,巧妙地设计了往返过程,起点终点都是同一个点,所以只牵涉了一个坐标的洛伦兹变换. 如果依旧要选用光的单向传播作为研究过程,就必须同时对两个端点的坐标进行变换,可以做如下推导. 如图4所示,在光线单向传播过程中,从直杆所在的参考系S来看,直杆的长度应该为L=x2-x1.从地面上的观察着来看,直杆的长度应该为 图4 洛伦兹变换下的“尺缩”效应 L′=x′2-x′1 根据洛伦兹变换有 则 化简后得 (13) 可以发现,根据洛伦兹变换,同时修正直杆初、末坐标的表达式,得出的结果与教材中利用光线往返运动获得的结论完全一样. 而在“钟慢”效应中,在运动的高铁车厢里由于教材设计的研究过程是光线竖直射出,与高铁的水平运动方向垂直,所以在这个方向上长度不会受到相对论效应的影响,即便换成单向性的过程,运算的结果也和往返过程得出的结果没有任何差异. 对于教材的处理,无论是教师备课还是学生学习,都要反复精读教材中的内容,阅读的同时需要不断思考教材的行文逻辑和编写意图. 本文从教材中“尺缩钟慢”效应证明的角度出发,对课本的证明过程提出质疑,通过对比教材选取的物理过程与自己建立的物理过程中在推理上的差异,进一步明确了如何通过建模、分析、推理去描述狭义相对论中的“尺缩钟慢”效应. 从教研、备课的角度来说,本文的再讨论可以是作为课堂教学以及各位同行在备课时对于这一章节的教学参考资料. 从教学的角度来说,结合单元教学设计,本文的论述可以作为一次单元教学设计的单元作业,学生在理解了狭义相对论的基本原理和“尺缩钟慢”效应后对于教材上的一些证明去探究新的研究方式,提出疑问的同时也展开研究,查阅资料做出合理的论述,这也是提升学生核心素养的一次机会.2.2 “尺缩”效应的证明

3 对教材中证明过程的质疑
3.1 对“钟慢”效应的质疑和论述
3.2 对“尺缩”效应的质疑和论述

4 对两种建模过程的再论述
4.1 洛伦兹变换

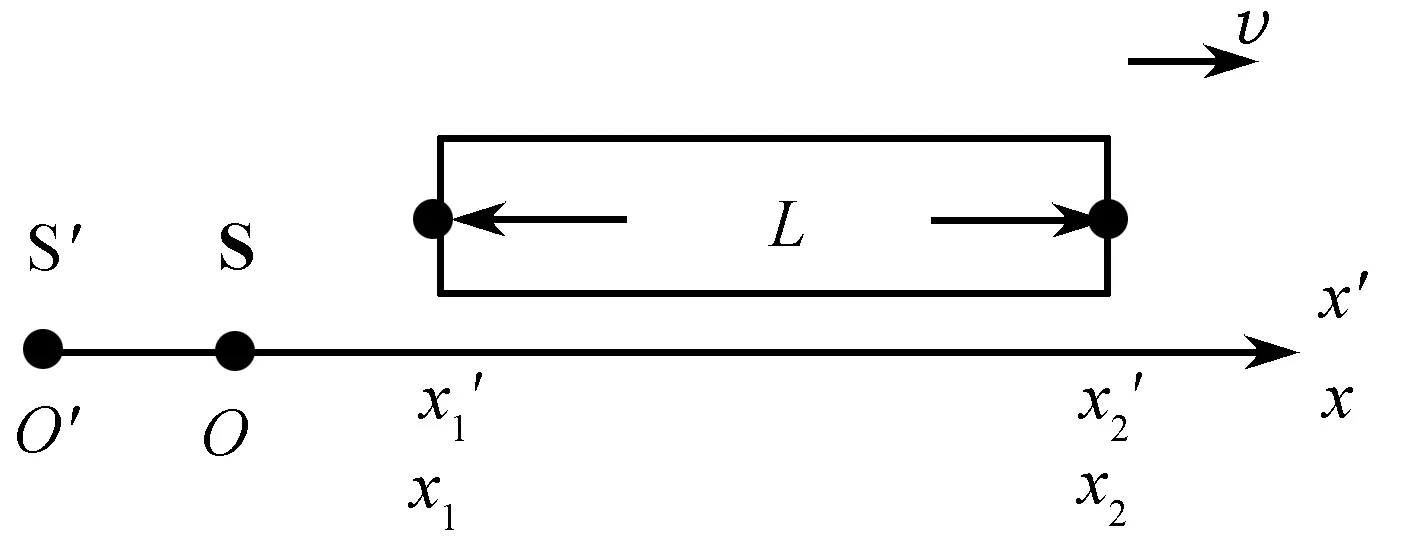
4.2 单向过程建模中存在的问题及原因阐述
5 结束语
