网球塔结构限制和稳定性分析
2023-10-10李滢滢黄欣琦
邓 欣 杨 益 鄢 然 李滢滢 黄欣琦 王 彪
(西南大学物理科学与技术学院 重庆 400715)
1 引言
通过每层3个网球、顶部1个网球的方式来堆叠建造一座塔,研究这种塔的结构限制和稳定性.当每层使用3个以上的球并且在顶层使用合适数量的球时,情况如何变化?这个问题来源于2022年IYPT(国际青年物理学家锦标赛).
2019年5月23日格鲁吉亚物理学家安德里亚在不使用任何胶带、胶水和其他黏合剂的情况下,仅利用网球表面的摩擦力成功搭建了一座9层小塔,刊登于PhysicsWorld杂志上.
网球塔搭建结构丰富多变,不同搭建结构下,网球塔的受力情况、稳定性和结构限制都将发生变化.网球塔搭建背后的理论依据涉及摩擦学、静力学、弹性力学等多个学类,该研究在工程、建筑方面有着广泛的运用,具有重要的研究价值.构建其理论模型将有助于相关建筑结构的研究.
2 3n+1网球塔结构稳定的条件分析
根据受力情况的不同,将3n+1网球塔结构整体分为3个部分,分别分析顶层球与次顶层球间的摩擦因数临界值、递推层之间的摩擦因数临界值、球与地面的摩擦因数要求.
在此处设定网球塔搭建为理想情况,具体是指将网球看成刚性小球,并且按照顺序致密排列,因此认为同层球之间不存在作用.本文中网球塔的层数用n来表示(不包括最顶层的网球),从上到下数层数,默认顶层的网球为第零层.
2.1 顶层次顶层球间摩擦因数的分析
2.1.1 角度分析
对于从顶部开始的3层球画出俯视图如图1所示,其中G为顶层球球心位置,A、B、C分别为次顶层3个球的球心位置,D、E、F分别为次顶球下方一层球的3个球的球心,其中K为A网球和B网球的接触点.角度分析几何示意图如图2所示.

图1 网球塔几何分析示意图

图2 角度分析几何示意图
假设θ角是该研究球的球心与上层球接触点的连线与竖直方向的夹角,根据几何关系可以知道
2.1.2 受力分析
由于网球塔结构具有对称性,取次顶层中一个球进行受力分析,如图3所示.该球受到自身的重力G、顶层球挤压的力N0以及顶层球的摩擦力f0,假设该球与顶层球的接触点与球心的连线和竖直方向的夹角为θ;下层球与其接触点为A点,A点与球心连线与竖直方向的夹角为φ.

图3 次顶层某一球受力分析图
此时根据平衡条件有
N0dsin (θ+φ)+mgdsinφ=
f0[r+dcos (θ+φ)]

2.2 递推层间摩擦因数的分析
2.2.1 角度分析
如图4所示,假设φ角是该研究球的球心与上层两球接触点的连线中点与竖直方向的夹角,其中K为A网球和B网球的接触点.
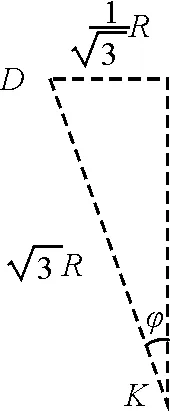
图4 角度分析示意图
根据几何关系可以知道
2.2.2 受力分析
对于递推层可以根据图5所示的受力分析图进行问题简化.根据上下层的对称关系,此时θ角的大小与φ角的大小相同.寻找通项公式(其中n表示当前网球层数,不包含最顶端的球,n∈N+,n>2).

图5 递推层某一球受力分析图
图5所显示的是网球在竖直平面上的投影,B点是转动轴(网球与下一层两球接触点的连线)的投影点.为方便对单个球的情况进行分析,我们设水平方向受到两个球对该球的作用力为2Fny,同理竖直方向上的力为2Fnz,绕转动轴,由力矩平衡方程可得
mgdsinφ+2Fnz·0=2Fny·2dcosφ
解得
再将Fny与Fnz分解在接触点支持力N的方向,以及分解在摩擦力f的方向上,即对于这个平面,有
Nnl=Fnzcosφ-Fnysinφ
fnl=Fnzsinφ+Fnycosφ
为分析三维受力,可以作出等效力投影分析示意图,如图6所示,其中yn、yn+1是选取的坐标轴,为两球心连线的方向.对实际球心位置进行分析,两个坐标轴间的夹角α为60°.

图6 等效力投影分析示意图

推荐理由:本书专门研究和论述战略思维。战略思维能力,就是高瞻远瞩、统揽全局,善于把握事物发展总体趋势和方向的能力。马克思主义为我们正确认识和妥善处理中国特色社会主义事业中诸多重大关系,树立全局眼光、提高统筹能力提供了思想武器。
F(n+1)y=-cosαFny+sinαFnx
可以解得
如图7所示,对第n层其中一个网球进行受力分析,这个网球会受到4个网球的作用力.以该球球心为原点,建立空间直角坐标系.

图7 中间层坐标系示意图
取球半径为R,由致密结构的几何关系可得4个接触点坐标
选取原点为参考点对研究对象进行受力分析,利用结构对称性,即同层球对该球在同方向上的分力大小相等,且支持力必沿两球球心可将关于力的平衡和力矩的平衡的6个方程简化为以下3个独立方程
∑Fy:f(n+1)y+f(n-1)y+N(n+1)y+N(n-1)y=0
∑Fz:2f(n+1)z+2f(n-1)z+
2N(n+1)z+2N(n-1)z=mg
其中f为摩擦力,N为支持力,下标(n+1)表示下层球对该球的作用力,下标(n-1)为上层球对该球的作用力.
由摩擦力与压力方向正交,可得以下2个独立方程
f(n+1)xN(n+1)x+f(n+1)yN(n+1)y+
f(n+1)zN(n+1)z=0
f(n-1)xN(n-1)x+f(n-1)yN(n-1)y+
f(n-1)zN(n-1)z=0
在x、z方向上整体受力有
又支持力必沿两球球心连线,故
则下层球与该球之间的静摩擦因数通过摩擦力与压力作比得到
243[96n(3n+1)-9]·[1024(3n+1)2+
摩擦因数与层数关系如图8所示.

图8 摩擦因数与层数关系图
2.3 底层球与地面间摩擦因数的分析
球与地面间摩擦受力分析如图9、图10所示.

图9 地面摩擦受力分析示意图(1)

图10 地面摩擦受力分析示意图(2)
以底层球与地面接触点D为平衡点,由力矩平衡方程可以得到
Fxl1=Fzl2
其中
可以解得
以底层球质心Q为平衡点,有
Fxl3+f1r=Fzl4
解得
由μ1N1≥f1,可以解得地面的摩擦因数
由此可以求出球与地面间的摩擦因数临界值.
3 一层多球的摩擦因数条件


图11 一层多球几何分析示意图(1)

图12 一层多球几何分析示意图(2)
顶层和次顶层球间的受力关系如图13所示.

图13 次顶层球受力分析图
由图13分析可得满足平衡条件
次顶层球绕接触点连线的轴由力矩平衡可得
N0dsin (θ+φ)+mgdsinφ=
f[r+dcos (θ+φ)]
对于正四边形,由图14所示的几何分析图可以得出角度关系

图14 一层4球几何分析图
代入计算可得此时顶层和次顶层间的摩擦因数应该满足条件
μ≥ 1.538 59
对于正五边形,由图15所示的几何分析图可以得出角度关系

图15 一层5球几何分析图
代入计算可得此时顶层和次顶层间的摩擦因数应该满足条件μ≥2,由此可知,一层4球和一层5球的情况下,要想搭建成功需要的摩擦因数大于3n+1结构所需的摩擦因数.
4 总结
综上所述,可以得到以下结论:
(1)mn+1结构搭建的网球塔,越低的层级所需的摩擦因数越小,最高一层网球需要的静摩擦因数最大.
(3)一层4球和一层5球的情况下,要想搭建成功需要的摩擦因数应大于3n+1结构所需的摩擦因数.
