基于CFD数值计算的大跨悬索桥碳纤维矩形截面吊杆风致振动研究

2023-10-10张建国

振动与冲击 2023年18期

张建国, 张春

(厦门大学建筑与土木工程学院,福建厦门 361005)

当今,在超大跨径桥梁的建设中,悬索桥毫无疑问是竞争力最强的一种桥型,其跨越能力是其他类型桥梁无可匹及的。吊索作为悬索桥的重要传力构件,其性能对悬索桥的影响巨大。由于吊索具有长细比大、质量轻、阻尼小等特点,使得在风荷载作用下其发生振动的概率大大增加[1]。

华旭刚等[2]强调长吊索和特长吊索的风致振动必须重点关注。马存明等[3]通过节段的静力和弹簧悬挂动力试验,对H型吊杆的驰振和涡激振动性能进行分析。陈政清等[4]对H型吊杆的大攻角风致振动进行探究并提出直立杆件抗风设计的建议。岳明[5]使用数值模拟的方法研究了悬索桥并列吊杆的涡激振动,该研究的重点为研究不同长度吊杆的涡激振动。研究发现吊杆越长,吊杆刚度越大,越容易发生涡激振动且发生涡激振动的风速较小,易造成吊杆的疲劳损伤。徐昕宇等[6]采用CFD(computational fluid dynamics)模拟,研究扁平板式吊杆风致涡激振动特性,发现开槽后的吊杆断面在各风速下振幅接近0,吊杆开槽能够有效抑制涡振的发生。

以上对悬索桥吊杆的研究都是基于传统的钢绞线或H型钢材料制作的吊杆进行风振探讨,本文提出利用新型碳纤维材料制作吊杆,探究吊杆风振特性。与传统钢绞线相比,碳纤维材料具有质量轻、强度高、耐腐蚀的特点,为桥梁的安全提供了有力的保障[7]。由于碳纤维材料特性,吊杆做成矩形截面的情况较多,然而矩形截面容易发生驰振现象,故而矩形截面吊杆仅在欧洲为数不多的几座桥梁上有所应用,国内桥梁应用的实例少,本文提出在满足力学性能要求的基础上,对矩形碳纤维吊索采用CFD方法研究不同风攻角、不同截面比对吊杆涡激振动以及驰振可能性的影响。

1 工程概况及自振频率

1.1 工程概况

国内某大跨度悬索桥吊杆选用碳纤维材料后的铰接式吊杆布置如图1所示。

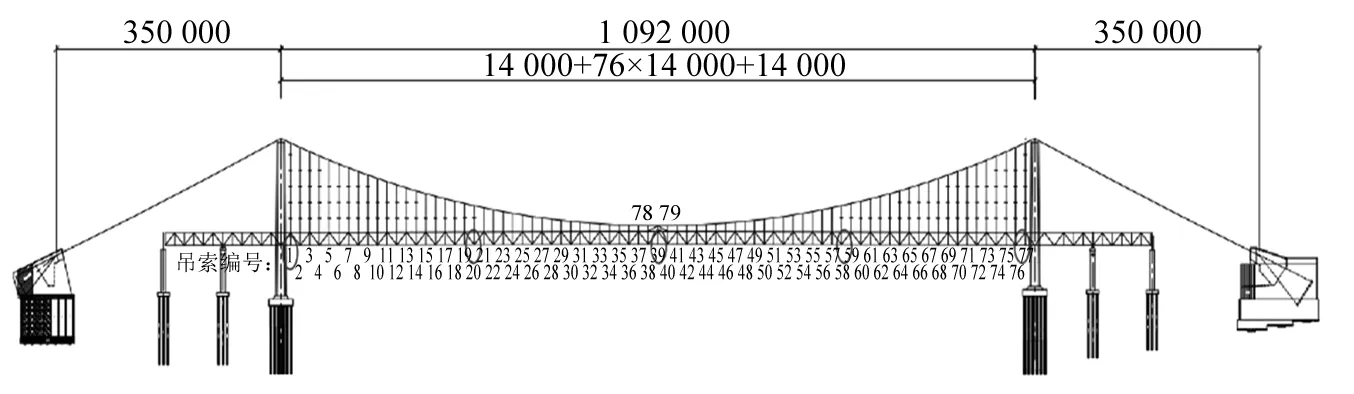
图1 吊杆编号Fig.1 Hanger number

在图1中选择具有代表性的5根吊杆进行研究,分别为左端部1号,1/4跨20号,跨中39号,3/4跨58号以及右端部77号,如图1圆圈所示。桥梁设计人员进行了设置碳纤维吊杆工况下大跨度悬索桥梁的受力分析和结构设计,求得更换后的典型碳纤维索截面积均为0.021 m2,密度为1.6 g/cm3,弹性模量为1.3×1011Pa,泊松比为0.307。表1为吊杆在重力荷载代表值下计算得到的索力值。

表1 替换后碳纤维索的索力

在进行吊杆风致振动研究时,可将吊杆简化为质量-弹簧-阻尼系统,那么要研究吊杆的涡激振动问题,最重要的就是确定吊杆的刚度K,而吊杆的刚度与吊杆的自振频率相关,因而确定吊杆的刚度问题也就转化为吊杆自振频率的求解问题。吊杆自振频率的求解有两种方法:有限元模态分析和理论公式计算法。

1.2 有限元模态分析

在ANSYS有限元分析软件中,采用LINK180单元用来模拟吊杆,计算选择Block Lanczos法计算前10阶频率,所得计算结果如表2所示。

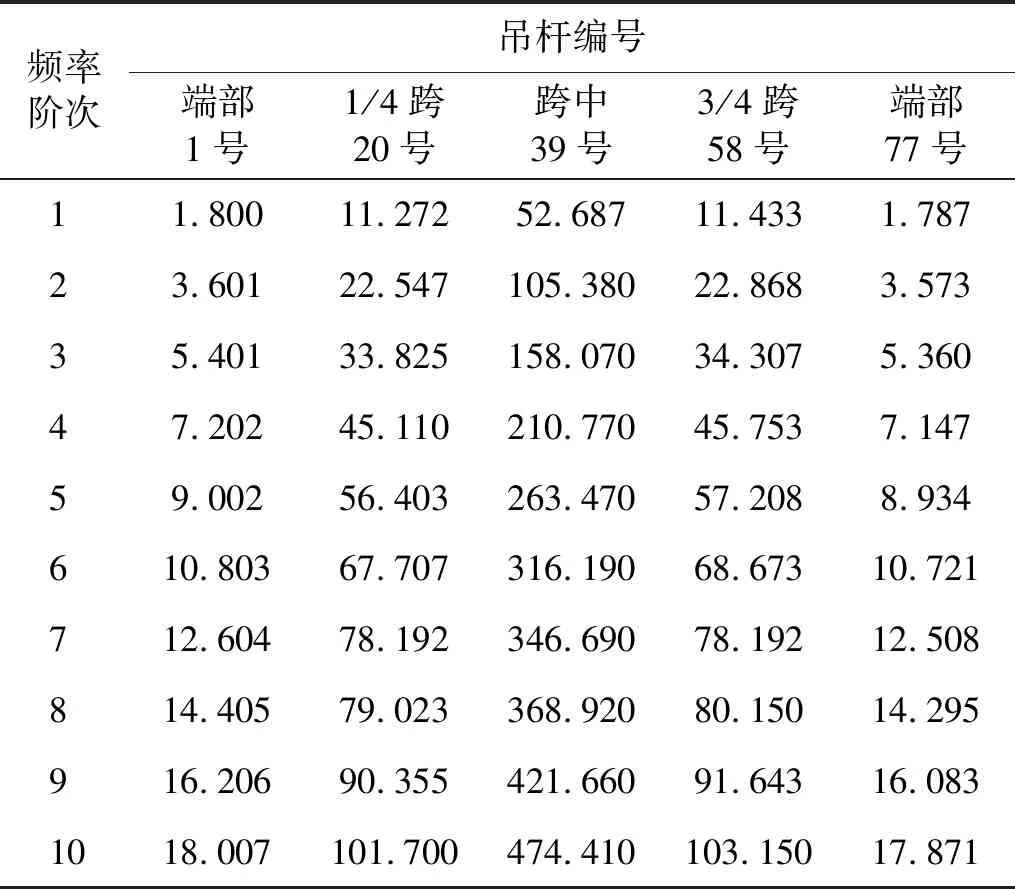
表2 吊杆自振频率

1.3 自振频率理论计算

为了验证吊杆模态分析所得到的自振频率的正确性,采用考虑预应力的吊杆自振频率理论计算公式进行吊杆的一阶自振频率计算。

Clough等[8]提出理论:当“弦”两端固定,不考虑抗弯刚度的影响时张力与频率之间的关系为

(1)

式中:T为吊杆张力;m为吊杆单位长度质量;l为吊杆长度;fn为吊杆第n阶横向振动频率。

参考表1给出的吊杆最大索力,计算转换为最大初张力,结合已知的碳纤维吊杆的物理参量,采用上述理论方法计算得到吊杆的一阶自振频率,并与有限元模态分析计算得到的吊杆一阶自振频率表2进行对比得到表3。

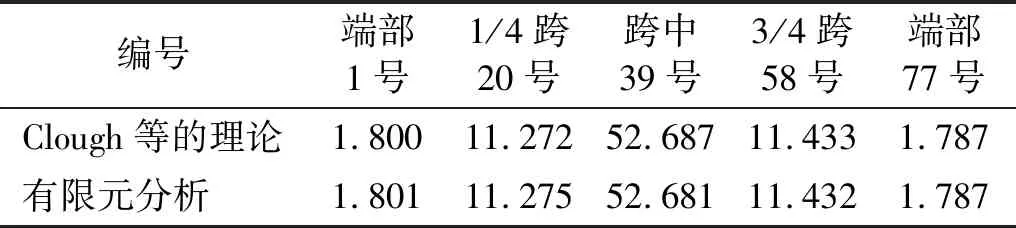
表3 吊杆一阶自振频率理论法和有限元法计算比较

由表3给出的吊杆一阶自振频率理论公式求解和有限元模态分析求解结果比较可知,理论公式法的结果与有限元模态分析求解的结果基本相同,说明本文的有限元模型有效,因此,可运用本文有限元模型求得的结果进行后续风致振动研究。另外,端部1号和端部77号两根吊杆的频率极其接近,而1/4跨20号和3/4跨58号两根吊杆的自振频率也很接近,因此,在后续的风致振动分析时,没有针对3/4跨58号吊杆和右端部77号吊杆进行研究,仅选取了1号、20号和39号3根吊杆进行详细分析。

2 CFD计算模型

2.1 控制方程

计算风工程又称数值风洞方法,与直接风洞试验相比具有模拟真实风环境的能力,可以构建原型尺度的计算模型,还具有周期短、费用低的特点。在直角坐标系下,对二维不可压缩黏性流体,其运动规律用纳维-斯托克斯方程(N-S方程)[9]描述

(2)

(3)

式中:ρ为空气密度;ν为运动黏性系数;u为速度矢量,f为作用在单位质量流体微团的质量力;p为流体压强。

2.2 数值模拟

对数值计算而言,计算域选取的大小对于结果的影响很大。从理论上来讲,计算域越大,与实际情形越接近,结果就会越精确。但由于计算机内存及时间的限制,不可能选取太大的计算域[10]。文献[11]认为计算域的进口、上下边界距柱体的距离至少为10D,出口距柱体的距离应大于20D,才能保证结果的独立性。本文计算域取为42D×24D,进口处距吊杆12D,出口距吊杆30D,上下边界距吊杆12D。此外,当流体流过钝体的时候,由于流体本身黏性的作用,使得物体表面上的流体速度为零,而离开物体表面一定距离的流体速度则不受黏性影响,此处的流动可以按照无黏来处理。在物面和流体之间的可以按无黏处理的这一部分流体就是边界层。边界层通常是很薄的一层,但在这一薄层中各项流体参数却发生着剧烈的变化,存在着较大的速度梯度。因此,在绕流问题中精确地模拟边界层对于结果至关重要,这就要求边界层网格要足够密[12],本文所划网格如图2所示。

图2 截面比为1 ∶1时计算域及网格示意图Fig.2 Schematic diagram of the calculated domain and mesh with a cross-section ratio of 1 ∶1

SSTk-ω模型合并了来源于ω方程中的交叉扩散,湍流黏度考虑到了湍流剪应力的传播,而且模型常量不同,这些特点使得该模型在近壁区域的自由流、逆压梯度流动、翼型、跨音速激波等方面有着更高的精度[13]。本数值模拟选择SSTk-ω湍流模型,具体数值模拟中,采用SIMPLE格式求解压力速度耦合方程组,空间离散采用二阶迎风格式,时间离散采用二阶全隐格式。已有的研究数据表明,方柱绕流的无量纲频率约为0.12,在一个涡脱落周期内至少需要20～25个时间步长[14],经计算后时间步长取Δt=0.02 s。

计算域边界条件设置如下:

(1)左侧,速度入口,U=U0,V=0。

(2)右侧,出口边界条件,平均静压P为零。

(3)沿展向两边界采用对称边界条件,各变量沿法向的分量为零。

(4)其余边界采用无滑移固壁边界条件,U=0,V=0。

2.3 模型验证

首先进行了网格独立性测试。对1 ∶1截面时0°攻角计算共选用了4种网格数量(时间步长均为0.02 s)进行了测试,网格独立性测试结果如表4所示。表5为已有文献单方柱0°攻角时绕流数据对比。

表4 网格独立性验证

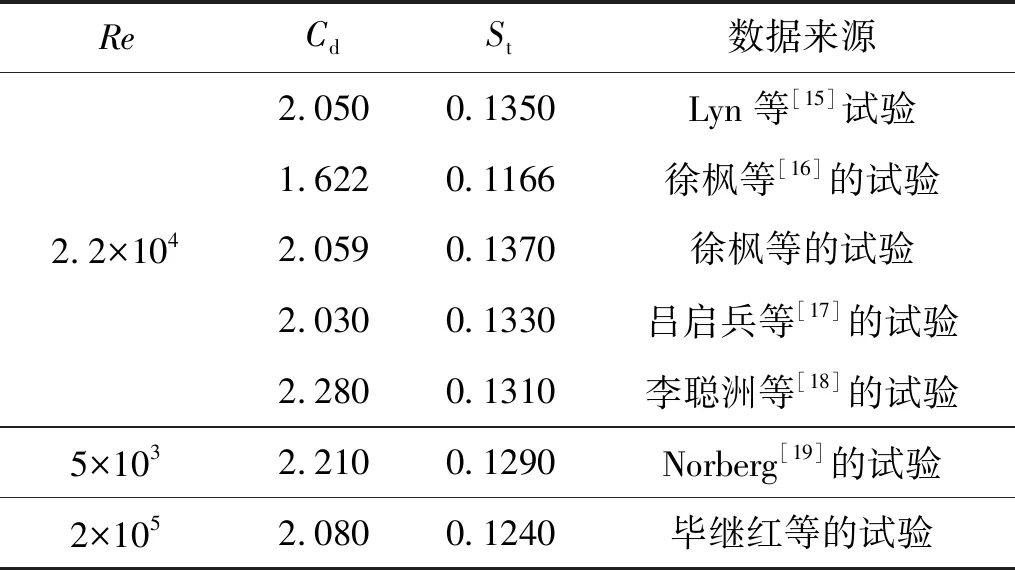
表5 文献单方柱0°攻角时绕流数据

根据表4和表5结果,选择40 000网格数进行后续计算既能满足计算精度要求,又能达到计算效率要求。

3 数值模拟结果

3.1 驰振判断

驰振是由于负气动阻尼引起的横风向结构振动,常出现在具有特殊截面形状的细长结构中。Den Hartog在研究覆冰导线时提出了横风向驰振判据式(4)。

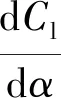
(4)

图3和图4为不同截面比且攻角为0°时的三分力系数时程曲线图;图5～图7为平均升力系数、平均阻力系数数值模拟结果以及不同截面驰振系数随攻角变化情况。

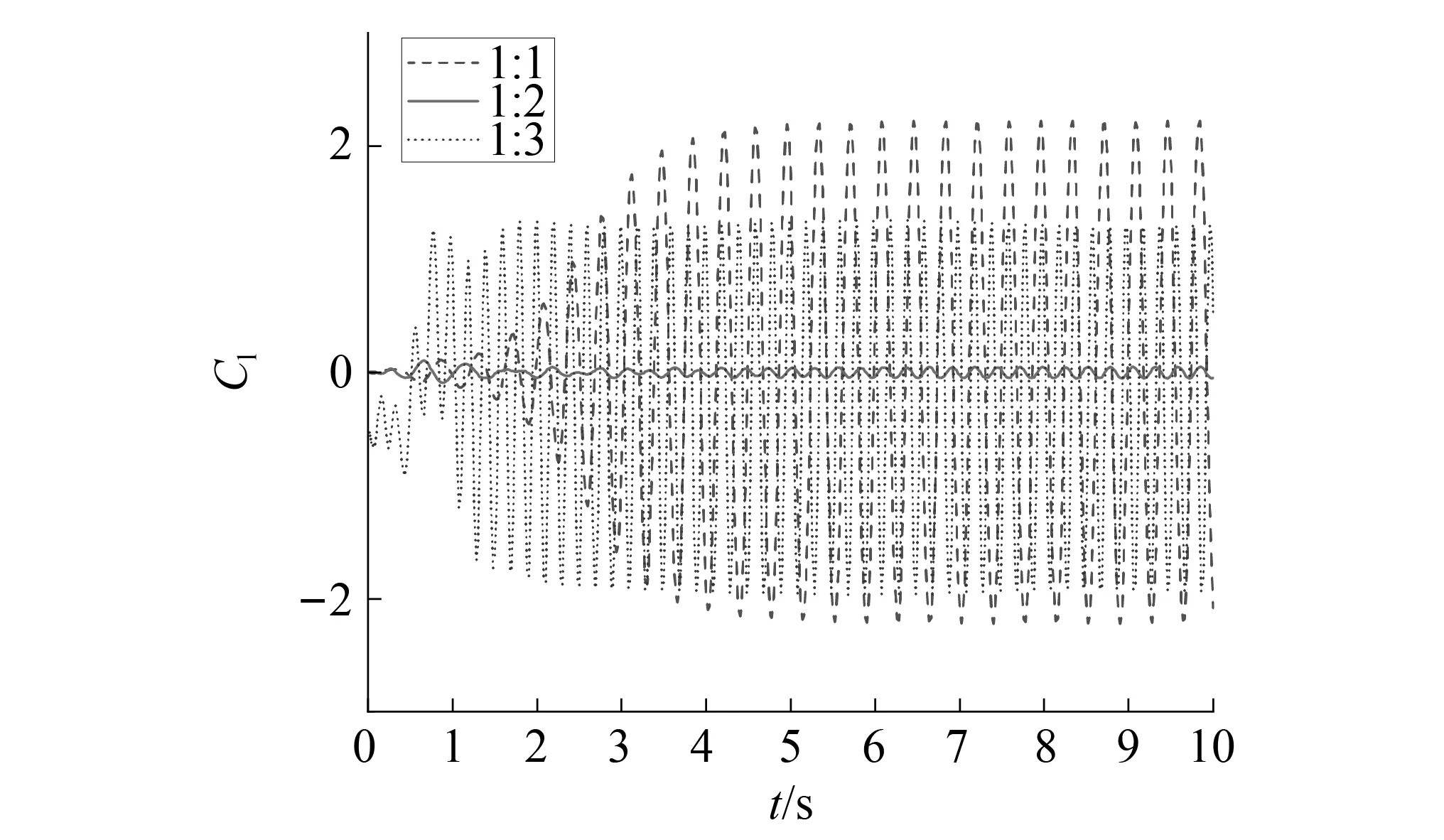
图3 攻角为0°时升力时程曲线Fig.3 Lift force time curve of 0° attack angle

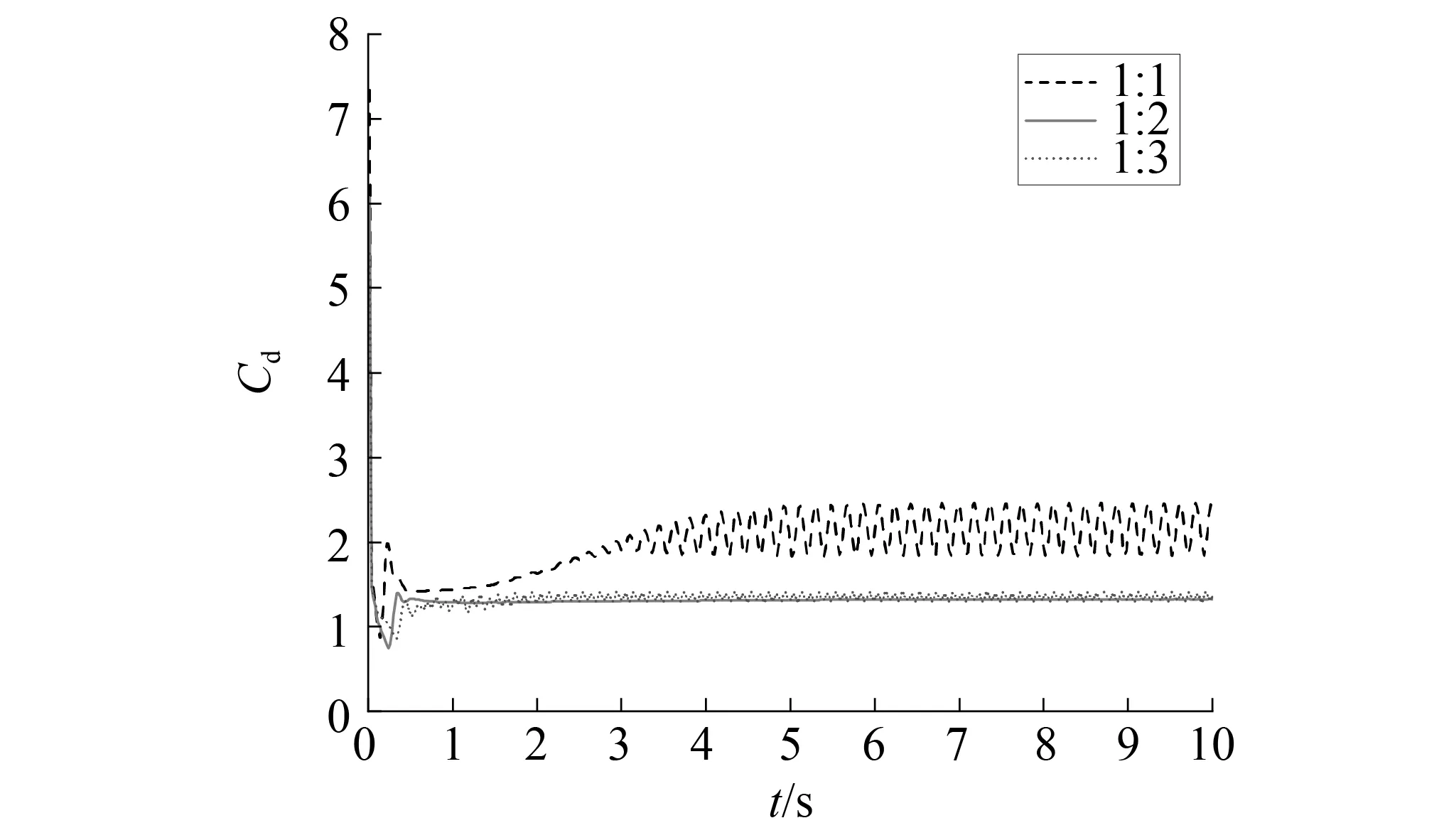
图4 攻角为0°时阻力时程曲线Fig.4 Damp force time curve of 0° attack angle

图5 平均升力系数随攻角变化曲线Fig.5 The mean lift coefficient varies with the angle of attack curve

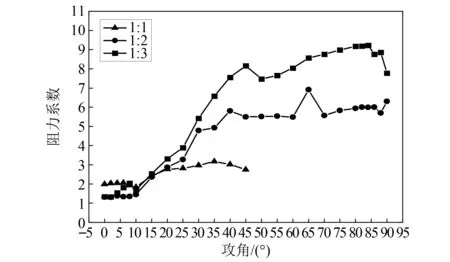
图6 平均阻力系数随攻角变化曲线 Fig.6 The mean damp coefficient varies with the angle of attack curve

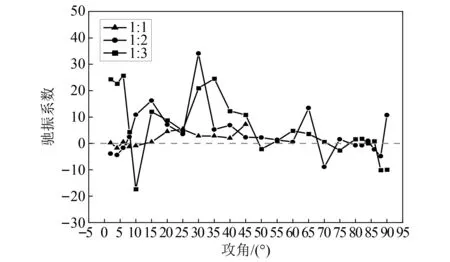
图7 不同截面驰振系数随攻角变化图 Fig.7 The galloping coefficient of different sections with the angle of attack

按准定常驰振理论[20],驰振临界风速如式(5)所示。

(5)

式中,B为相应的迎风面宽度,同时根据陈政清等的观点,认为维持稳定的驰振状态的区间应在一定攻角范围以内。按一般设计思想取最小驰振系数进行计算,虽然最为保守但实际上却是明显不合理的。因为在实际的紊流风作用下杆件风攻角(即风场的方向角)是变化的,攻角大于驰振度数后杆件会迅速退出驰振状态,故而认为取处于稳定的驰振区间的平均值较为合理。表6为不同截面比矩形吊杆的临界驰振风速计算结果。

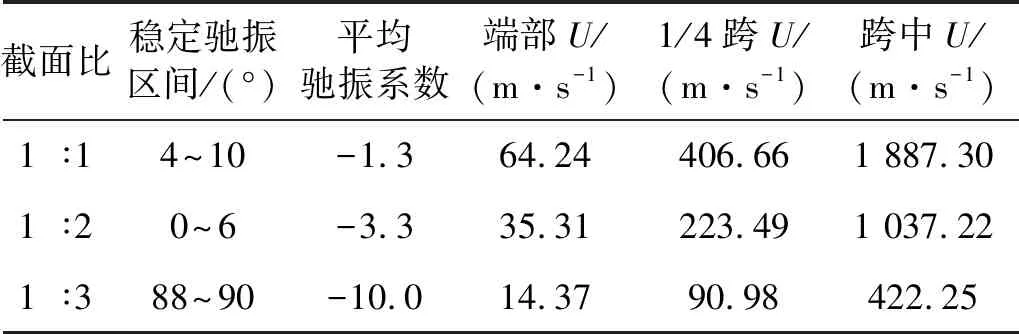
表6 临界驰振风速计算结果

按照Parkinson等于1964 年提出的非线性准定常模型可知,此理论中横风向脉动气动力系数可以表示成

(6)

CFY可以由柱体静风试验直接测量得到的平均升力系数和平均阻力系数推算求得

CFY(β)=-[CL(β)+CD(β)·tan(β)]·sec(β)

(7)

利用该数学模型预测所得柱体气动失稳(驰振)临界风速

(8)

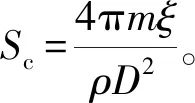
对1 ∶1截面所得数据进行处理后,曲线拟合所得系数A=1.27,B=29.54,C=72.51,D=55.92,代入式(8)中计算可得该模型预测1 ∶1截面比时驰振临界风速为端部吊杆临界驰振风速为66.08 m/s,1/4跨处吊杆临界驰振风速为413.80 m/s,跨中吊杆临界驰振风速为1 934.18 m/s。表6中计算数据与此模型计算结果相差不大,数据可信。

根据表6结果,可知对于跨中及1/4跨处吊杆,计算出的临界驰振风速均较大,大于悬索桥的设计风速,即不用考虑吊杆驰振。对于端部吊杆而言,当截面比为1 ∶1和1 ∶2时不用考虑驰振情况,但是当截面比为1:3时,端部吊杆相应的临界驰振风速较低,需要考虑相应的抗驰振措施。

3.2 涡振判断

当大气边界层中近地风绕过桥梁时,可能会产生流动分离和周期性的旋涡脱落,使结构上下或左右两侧表面出现交替变化的正负压力和力矩,称为涡激力。涡激力可能会引起结构横风向或扭转方向有限振幅的振动,称为涡激振动,简称涡振。涡振虽然不会像驰振、颤振一样导致桥梁产生灾难性的破坏,但是它发生时的风速低、频率高,有可能导致杆件裂纹或疲劳破坏,或影响行车的舒适性和安全性[21]。

对FLUENT计算得到的1 ∶1吊杆的力矩系数Cm时程数据进行FFT(fast Fourier transformation)后可以得到其频谱图如图8所示。可见力矩系数频谱存在明显的峰值频率。

图8 截面为1 ∶1 0°攻角时力矩频谱图Fig.8 FFT of the moment coefficient at 0°attack angle and 1 ∶1 cross section

汇总所有风向角下3种不同截面吊杆力矩系数的峰值频率数据,给出斯特劳哈尔数St如式(9)所示。

St=fSD/U

(9)

式中:fs为旋涡脱落频率;U为本次数值模拟中的平均风速,3 m/s。图9即为主频对应的斯特劳哈尔数随风攻角变化图。

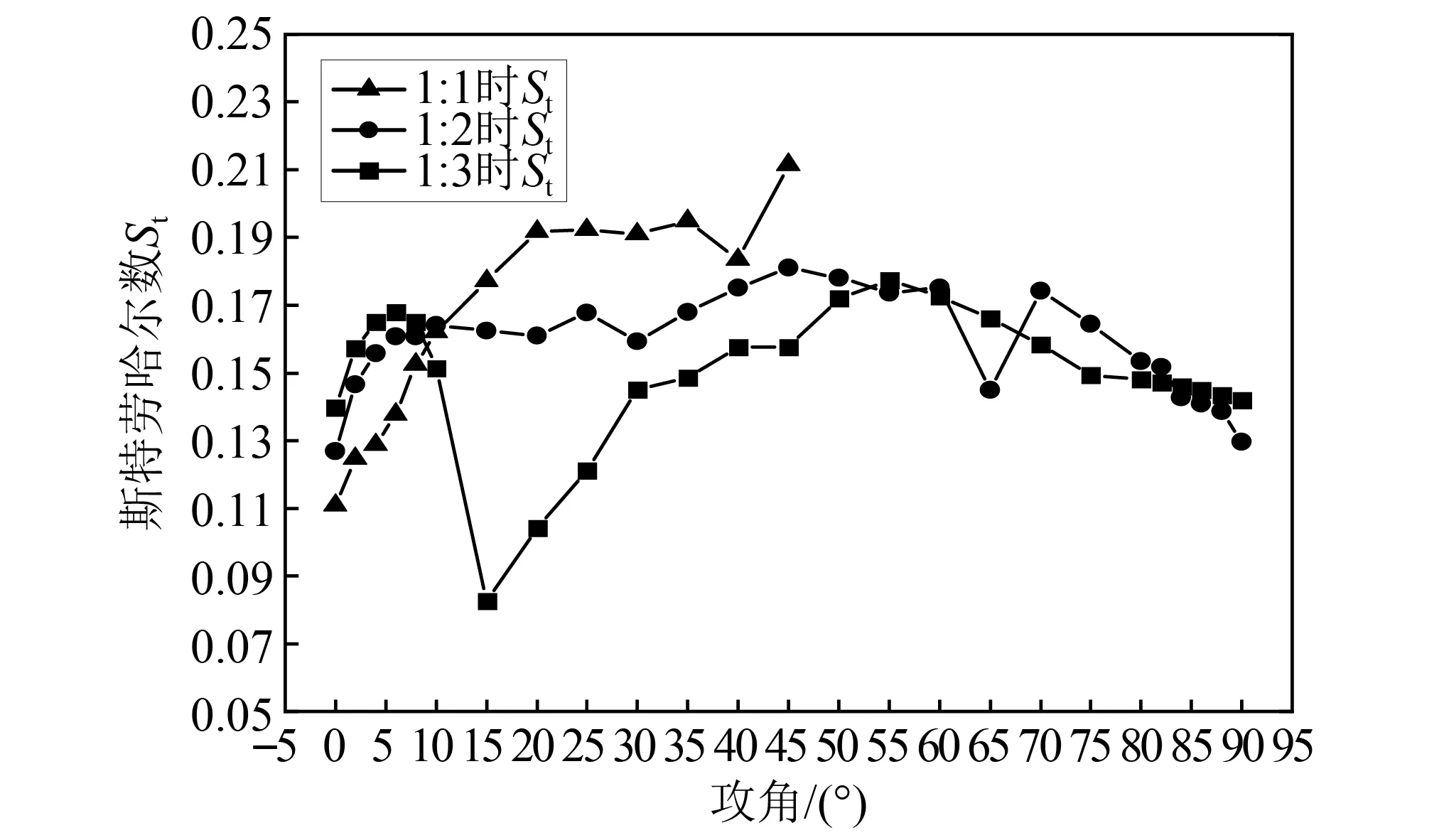
图9 主频对应的斯特劳哈尔数随风攻角变化图Fig.9 The main frequency corresponding to the Strouhal number changes with the attack angle

对于吊杆,如果旋涡脱落的卓越频率fs与在横向风作用下吊杆振动特征频率f相同,就会导致涡激共振。因此,由fs=f定义的临界风速Ucrit为式(10)。

(10)

Sohankar[22]的研究发现无论边界层的性质如何,尖锐边缘的物体都会导致流动分离,但尤其是在较高的雷诺数下对雷诺数不敏感。由于本文研究的吊杆为矩形截面,且研究为高雷诺数情况,因此可不考虑雷诺数的影响。而Re=UD/ν,即在此次研究中不考虑空气运动黏性系数以及特征长度的改变,也就是说Re仅与风速有关,即本次研究中风速的改变基本上对St无影响。由此知D/St越小,同时自振频率越小,则涡振风速越小,故而对不同截面比的吊杆取相应的D/St最小值,用对应吊杆自振频率进行计算,可以推算其最小涡振风速见表7。由表7可知,端部吊杆在3种截面比情况下,均容易发生多阶的涡激振动,最小涡振风速都较小,而1/4跨和跨中吊杆,在3种截面比时,仅可能发生低阶的涡振,高阶涡振对应的风速均较大。

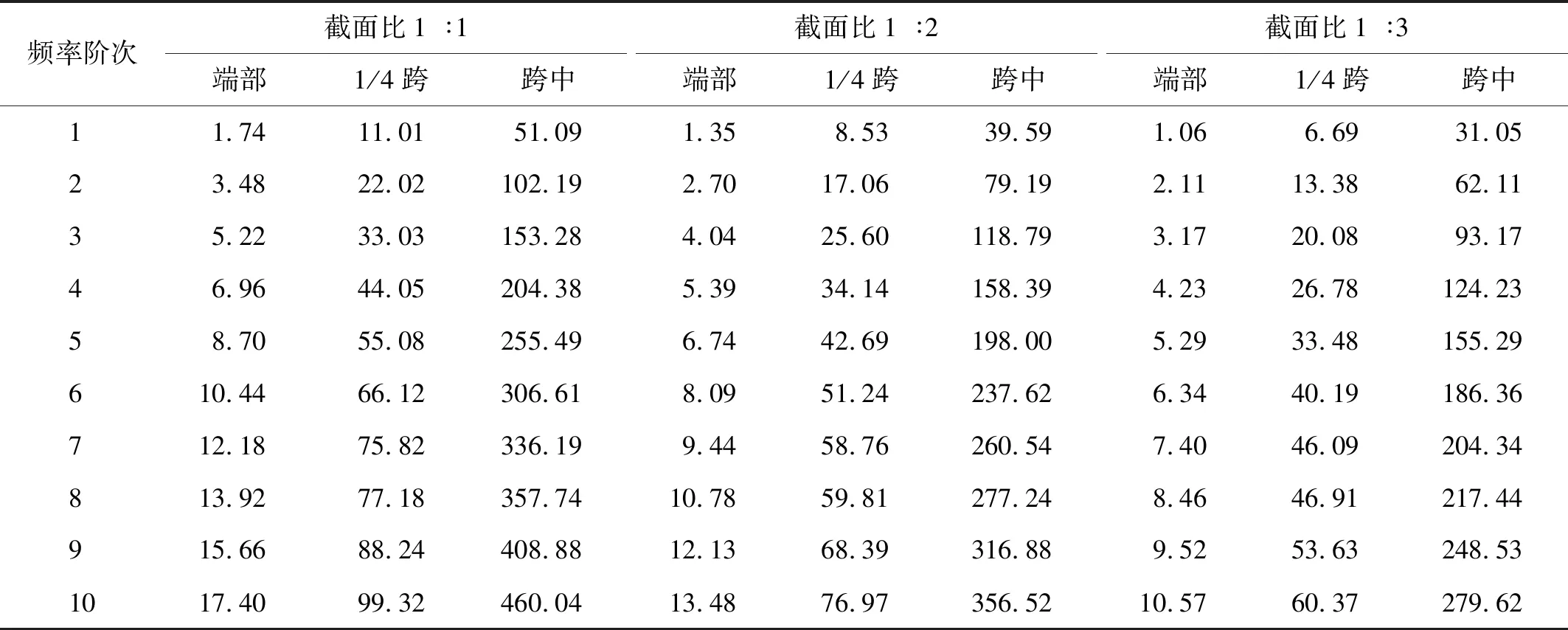
表7 涡振风速

3.3 流场分析

基于FLUENT后处理软件绘制本次数值模拟中二维矩形断面的风速云图及风压云图,本文通过这些云图来分析吊杆周围的流场分布情况,进一步说明矩形吊杆的涡激共振的机理,具体云图如图10所示。需要说明的是,由于本文没有进行流固耦合分析,流场分析中未出现“频率锁定”现象。

图10 风速云图(左)与风压云图(右)Fig.10 Wind speed cloud graph (left) and wind pressure cloud graph (right)

从云图中可以看出,气流在吊杆的上下侧出现明显的来流分离和旋涡脱落,并在吊杆后方产生空腔。吊杆上下侧旋涡交替脱落以及吊杆后方的空腔是引起吊杆涡振的重要因素。吊杆后方的尾流区上下两侧旋涡交替反向,总有一侧的尾涡占主导地位。随着截面比变小,流体附着点越多,出现再附着的可能性更大。随着攻角变化,分离点发生变化,同时附着点也发生变化,对于非正方形截面,当吊杆处于大风攻角时,尾流相较而言紊乱得多。对于吊杆,迎风面所受风压大,在尾部形成负压区,同时尾流区散布负压区。