含弹性约束碰撞振动系统的不连续分岔

金 花, 张锦涛, 吕小红, 王 昕

(兰州交通大学 机电工程学院,兰州 730070)

机械力学领域广泛存在的含间隙碰撞振动系统是一类很有代表性的分段光滑系统,具有丰富而复杂的动力学行为,并对机械系统的使用效率和性能等因素具有重要的影响。因此,碰撞振动系统动力学研究得到了国内外学者的充分重视。

对碰撞振动系统进行动力学分析时,根据碰撞体的刚硬程度将碰撞模型分为刚性碰撞和弹性碰撞。弹性碰撞模型考虑了碰撞时间和碰撞过程中的接触力变化。针对单自由度弹性碰撞振动系统,Peterka等[1-2]应用数值仿真方法研究了周期运动的擦边、周期倍化和鞍结分岔;Ing等[3]利用半解析法和试验研究了擦边轨道邻域内的动力学;Kundu等[4]考虑4种弹性约束配置,研究了擦边轨道邻域内范式映射的特性。擦边分岔有连续的和不连续的擦边分岔两种形式。Jiang等[5-6]研究了倍化型和鞍结型擦边分岔在弹性和刚性碰撞振动系统中的不同特征,并将不连续几何分析方法应用于弹性碰撞振动系统,解释了非碰撞运动与周期一碰撞运动之间的擦边分岔是否连续的原因。

近几十年来,研究者试图将光滑动力系统动力学研究的方法应用到非光滑动力系统,并取得了一定的成功。金俐等[7]等利用局部映射方法推导了刚性约束和弹性约束碰撞振动系统Poincaré映射的Jacobi矩阵。徐慧东等[8]针对弹性碰撞振动系统,利用转换矩阵方法得到全局的单值矩阵,通过Floquet理论分析了周期运动的分岔。张华彪等[9]利用参数延续打靶法研究了Jeffcott 转子碰摩系统周期运动的全局行为。张惠等[10]利用胞映射法研究了含间隙和弹性约束振动系统共存吸引子的吸引域变化机理。Tan等[11]结合胞映射和打靶法讨论了单自由度含对称弹性约束振动系统擦边轨道邻域内的多稳态行为与混沌演化。

随着计算科学的发展,Luo等[12]提出了多参数协同仿真分析方法,研究了两自由度含间隙刚性约束[13-14]、弹性约束[15]和对称刚性约束碰撞系统在两参数平面的周期运动模式及其分布规律,发现在相邻基本周期碰撞运动的两参数转迁过程中可能存在迟滞域和亚谐包含域两种特殊转迁域。由于多参数协同仿真分析是数值分析方法,只能求解系统的稳定周期运动和混沌,因此,Luo等只是讨论了两种特殊转迁域内的稳定周期运动模式及其分布规律,没有考虑包括不稳定周期运动的多吸引子共存现象。两种特殊转迁域的形成机理以及转迁域内部共存吸引子的分岔特征至今没有被完全揭示。打靶法是一种计算动力系统周期运动的常用方法。结合延拓打靶法和Floquet 理论可计算并追踪共存周期运动的稳定性与分岔。因此,本文考虑单自由度弹性碰撞振动系统,应用多参数协同仿真分析方法辨识系统在两参数平面的周期运动模式及其参数域,结合延拓打靶法和Floquet理论研究相邻周期运动转迁过程中的共存吸引子及其分岔,揭示迟滞域和亚谐包含域的形成机理以及转迁域内的全局动力学。

1 力学模型及运动微分方程

考虑弹性碰撞的线性振子和非线性振子都属于非光滑动力系统,不仅可以发生光滑动力系统中的各种常规分岔,还具有一些光滑动力系统不具备的特有分岔。因此,本文考虑图1所示单自由度含弹性约束线性振动系统的力学模型,受简谐激励力Psin(ΩT)作用的振子由刚度为K1的线性弹簧和阻尼系数为C的黏性阻尼器连接于支承。振子的质量为M,位移用X表示。B为振子与约束之间的间隙。约束用刚度为K2的线性弹簧描述。系统的运动微分方程为

图1 弹性碰撞系统的力学模型Fig.1 Mechanical model of elastic impact system

(1)

(2)

将式(1)写成规范形式

(3)

(4)

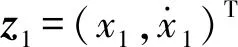
(5)

a1=x0-A1cos(ωt0)-B1sin(ωt0)

,

(6)

a2=x1-A2cos(ωt1)-B2sin(ωt1)-kb

,

(7)

2 局部复合映射

为了研究系统在两参数平面的周期运动模式及分岔,选择Poincaré截面Π0={(z,t):mod(t,2π/ω)=0}构建Poincaré映射P:Π0→Π0。系统的一条由z0点出发再返回z0点的1/1周期运动轨线(周期运动用p/n表示,n为激励力周期数,p为轨线穿越非光滑界面Σ1的次数),如图2所示。图2中:z0∈Π0;z1∈Σ1;z2∈Σ2;t1+t2+t3=T=2π/ω。轨线在0时刻从z0点出发在区域G1中经过时间t1抵达z1点,定义相位面Π1={(z,t):t=t1},建立局部映射P1

图2 1/1周期运动轨线Fig.2 Trajectoryof 1/1 periodic motion

P1:Π0→Π1, (z0,0)(z1,t1)

(8)

映射P1是通过解流形φ1(t)的光滑映射。因此,其Jacobi矩阵DP1为可通过多元函数求导法则得到

(9)

在t1时刻,轨线离开G1区域穿越非光滑界面Σ1进入G2区域,用局部映射P2表示。映射P2所花的时间为0。非光滑界面Σ的法向量为hz=[1,0]T,计算映射P2的Jacobi矩阵DP2为

(10)

轨线在t1时刻从z1点出发在区域G2中经过时间t2抵达z2点,定义相位面Π2={(z,t):t=t1+t2},建立局部映射P3

P3:Π1→Π2, (z1,t1)(z2,t1+t2)

(11)

映射P3是通过解流形φ2(t)的光滑映射,Jacobi矩阵DP3为

(12)

在t1+t2时刻,轨线离开G2区域穿越非光滑界面Σ2进入G1区域,用局部映射P4表示。与t1时刻相同,DP4=I。

Poincaré映射P可以表示为以上局部映射的复合。由于DP2=I和DP4=I,因此

PΠ0→Π0=P′1∘P3∘P1

(13)

式中:P′>1:Π2→Π0; (z2,t1+t2)(z0,T)。根据复合映射的链式求导法则,映射P的Jacobi矩阵为

DP=DP′1×DP3×DP1

(14)

若周期轨线在由z0点返回z0点的过程中没有穿越界面Σ1,此时系统为光滑动力系统,表现为0/1周期运动,Poincaré映射P为

PΠ0→Π0=P1, (z0,0)(z0,T)

(15)

当周期轨线从z0点出发经历n个力周期返回z0点,穿越界面Σ1一次时,系统做1/n周期运动。此时Poincaré映射P为

PΠ0→Π0=P1′∘P3∘P1, (z0,0)(z0,nT)

(16)

当周期轨线在由z0点出发经历n个力周期返回z0点的过程中p(p>1)次穿越非光滑界面Σ1时,系统做p/n周期运动,此时的Poincaré映射P由2p+1个局部映射复合而成,即

P=P′1∘(P3∘P1)(p)

(17)

其Jacobi矩阵DP为

DP=DP′1×(DP3×DP1)(p)

(18)

3 延拓打靶法

为了研究系统的全局动力学行为,本文应用基于Poincaré映射的打靶法及Floquet理论求解系统的共存周期解与稳定性。由于周期运动对应Poincaré映射P的不动点,则式(3)的周期解可以看作常微分方程的两点边值问题

(19)

式中,T=2π/ω,n= 1, 2, 3,…。z0∈Π0需迭代改进,直到满足边界条件为止。采用Newton-Raphson迭代法

(20)

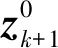
(21)

式中: Δv为分岔参数步长;Q(vk,zk)=P(vk,zk)-zk, ∂Q(vk,zk)/∂z=DP(vk,zk)-I。 ∂Q(vk,zk)/∂v可由式(22)以[zk,0]为初始值积分n个激励力周期T得到。

(22)

其中

(23)

上述计算过程中,在求得不动点的同时得到了Poincaré映射的Jacobi矩阵DP(zk)的特征值,根据Floquet理论可判断周期运动的稳定性与分岔。

4 两参数平面周期1运动的分岔特征

仿真结果表明,当k=9和ξ=0.06时,(ω,b)参数平面的区域H={0.1≤ω≤0.8, 0.1≤b≤1.3}内包含系统全部的周期1运动模式。因此,为了研究相邻p/1周期运动的两参数转迁规律,取H为考察区域,根据式(4)～式(7)计算系统的稳定周期运动模式及其参数域如图3所示。可见,在H内,除占据主导地位的p/1(p=0, 1,…, 5)类周期运动的参数域外,还存在很多主要囊括p/2类亚谐周期运动的小区域。为了方便分析,把这类小区域统称为亚谐包含域。用Lp/1∩(p+1)/1表示p/1和(p+1)/1运动的参数域分界线,用SIRp表示位于或邻近分界线Lp/1∩(p+1)/1的亚谐包含域。在p/1与(p+1)/1运动的转迁中出现的迟滞域用HRp表示。由图3可知,系统在SIRp内表现的周期运动模式主要有(2p+1)/2和2(p+1)/2等。当p=0和1时,亚谐包含域SIRp出现在(p+1)/1运动的参数域内邻近分界线Lp/1∩(p+1)/1的位置,而当p> 1时,亚谐包含域SIRp呈现于波浪状边界线Lp/1∩(p+1)/1的波峰处。由于亚谐包含域所处的位置有两种情况,因此,相邻p/1类运动经亚谐包含域的转迁呈现两种不同的特征。

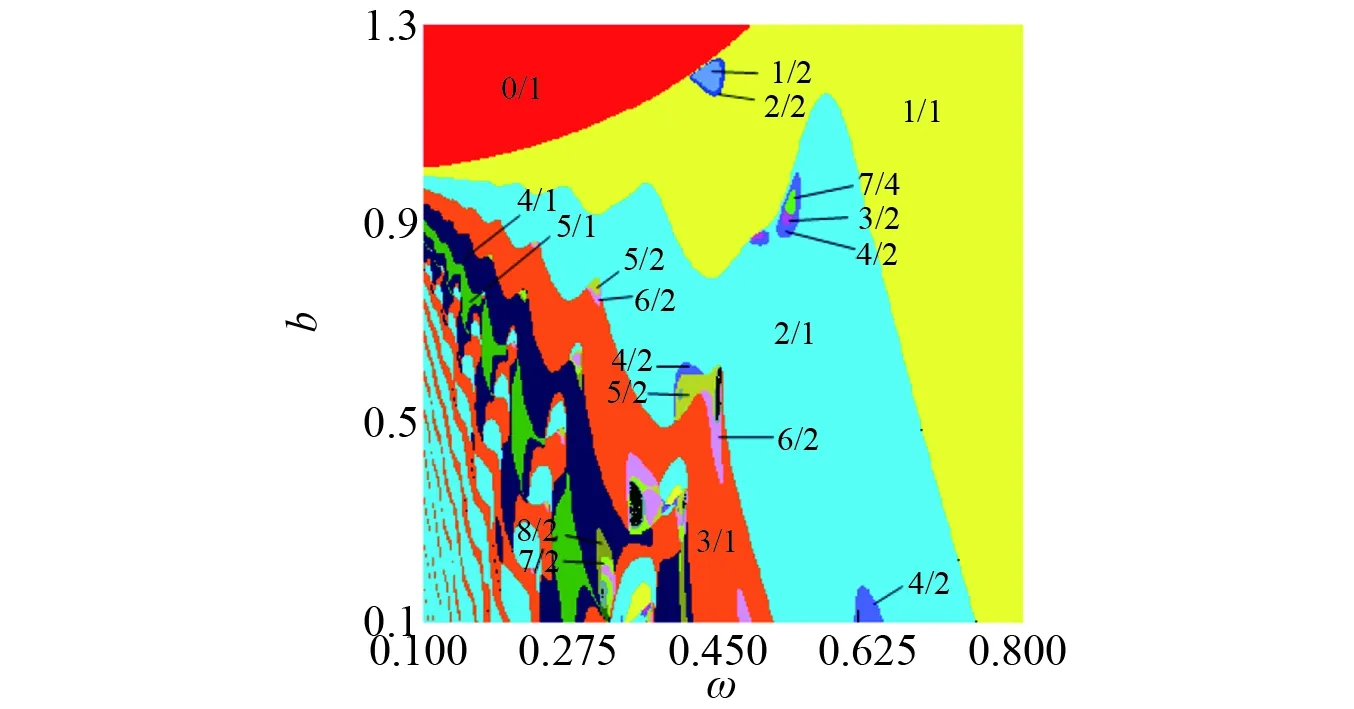
图3 两参数分岔图Fig.3 Two-parameter bifurcation diagram

4.1 两类擦边分岔

本节分析1/1与2/1运动之间的分岔,揭示p/1与(p+1)/1(p=0, 1)运动的转迁规律。取b=0.1,应用延拓打靶法计算1/1与2/1运动转迁的单参数分岔图如图4(a)所示。b=0.91,ω穿越亚谐包含域SIR1时的分岔图,如图4(b)所示。在图4(a)和图4(b)中,实线和虚线分别表示稳定和不稳定的周期运动。由图4(a)可知,减小ω,1/1运动经鞍结型擦边分岔(GR-SN1)产生2/1运动。分岔点GR和SN1之间的距离Δω=0.000 734 71。当ω=0.738 611 06(GR)时,1/1运动发生擦边分岔产生2/1运动。紧接着当ω=0.737 876 35(SN1)时,Floquet特征乘子为λ1=0.360 00,λ2=0.999 99,2/1运动经鞍结分岔消失,系统响应跳跃为另一个稳定的2/1运动。相反,当ω增大时,开始于ω=0.73的2/1运动在ω=0.743 858 75(SN2)处经鞍结分岔消失,系统响应跳跃为1/1运动。不稳定周期运动U2/1分支连接2个鞍结分岔点SN1和SN2,从而在1/1与2/1运动的转迁过程中形成迟滞区。迟滞区内,2个2/1运动和U2/1运动在点SN1和GR之间共存,而在点GR和SN2之间,1/1,2/1和U2/1运动共存。共存周期运动的相图和Poincaré映射图如图5(a)～图5(c)所示。图中的小面板描述了非光滑界面Σ0邻域内红色相轨线的细节。其中图5(b)的红色相轨线与∑相切,切点z*>∈Σ0,1/1与2/1运动经擦边分岔互相转迁。GR点的擦边分岔是连续的,但是,擦边诱导的鞍结分岔SN1使系统响应不连续。共存周期运动的吸引域演化如图5(d)～图5(f)所示。鞍结分岔使吸引域的拓扑结构发生突变,导致共存吸引子出现或消失,而擦边分岔不会引起吸引域的拓扑结构发生突变。

图4 1/1与2/1运动的分岔Fig.4 Bifurcations between 1/1 and 2/1 motions

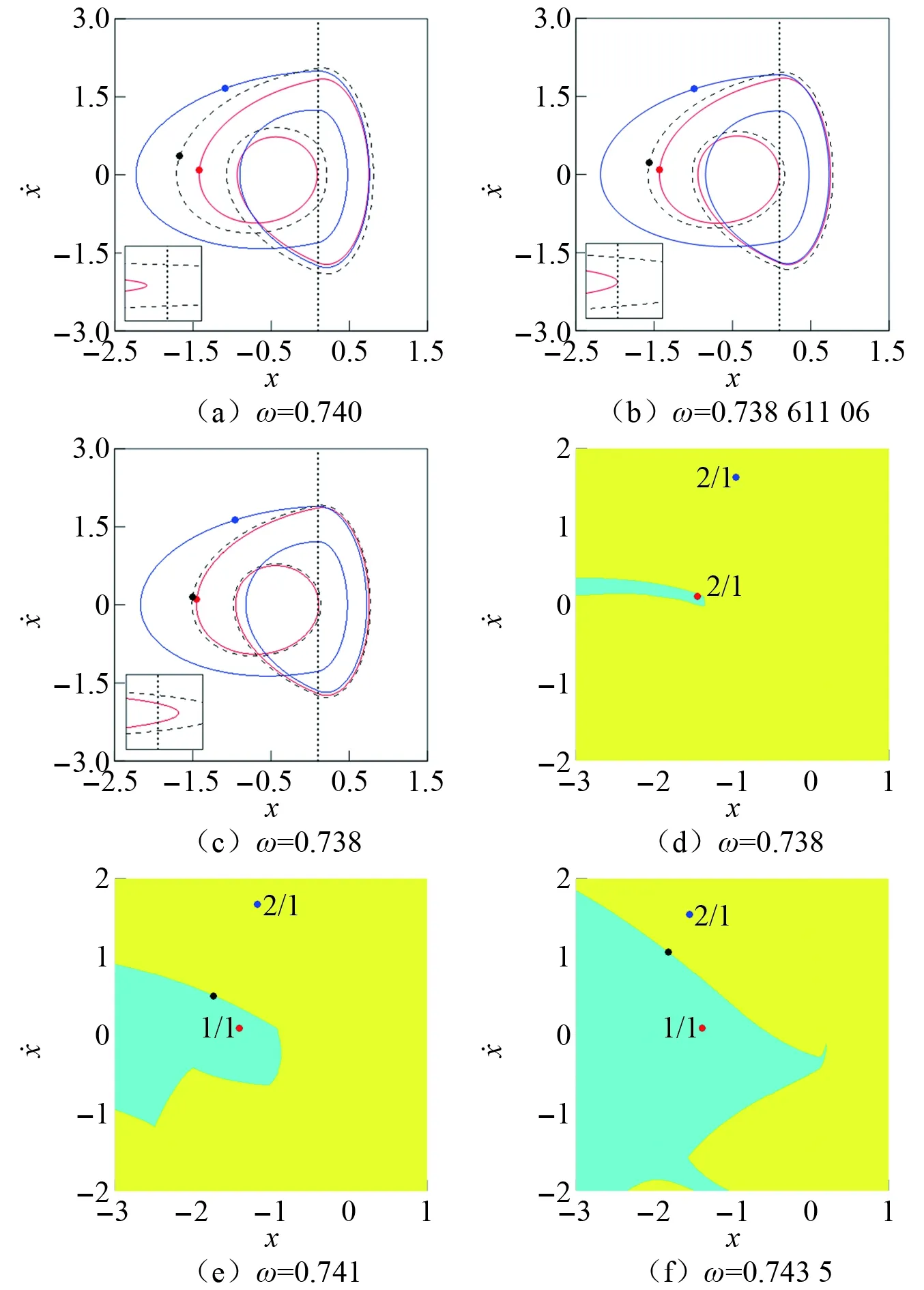
图5 相图、Poincaré映射图和吸引域,b=0.1Fig.5 Trajectories, Poincaré maps and basins of attraction, b=0.1

由图4(b)可知,增大ω,1/1运动经周期倍化型擦边分岔(GR1-PD1)产生U2/1运动。分岔点GR1和PD1之间的距离Δω=0.004 743 26。当ω=0.508 742 45(GR1)时,系统发生1/1运动的擦边分岔。随后在ω=0.513 485 71(PD1)处,Floquet特征乘子为λ1=-0.230 36,λ2=-1.000 01,周期倍化分岔使2/1运动失去稳定性。继续增大ω当ω=0.536 450 39(PD2)时,系统再次发生周期倍化分岔使U2/1运动恢复稳定。产生于PD1点的4/2运动在ω=0.517 770 45(GR2)处经擦边分岔产生3/2运动,然后在ω=0.529 939 29(GR3)处返回4/2运动。PD1和PD2为亚谐包含域SIR1边界上的点。结合图3和图4(b),ω穿越亚谐包含域SIR1的分岔可归纳为

(24)

应用延拓打靶法计算1/1和2/1运动相互转迁的(ω,b)参数分岔线,结果见图4(c)。图4(c)中,不同类型的分岔线用不同的颜色区分。红色和绿色鞍结分岔线包围的区域为迟滞域。其中,红色分岔线紧贴蓝色擦边分岔线,因此,1/1运动的鞍结型擦边分岔(GR-SN1)在1/1与2/1运动的转迁过程中产生迟滞域HR1。迟滞域分布在波浪状分界线L1/1∩2/1的波峰爬升区,随着波峰的减小而减小。其余参数区域内,1/1与2/1运动经擦边分岔连续转迁。亚谐包含域SIR1被黑色周期倍化分岔线包围,左侧紧靠擦边分岔线。因此,1/1运动的周期倍化型擦边分岔(GR-PD)产生亚谐包含域SIR1。

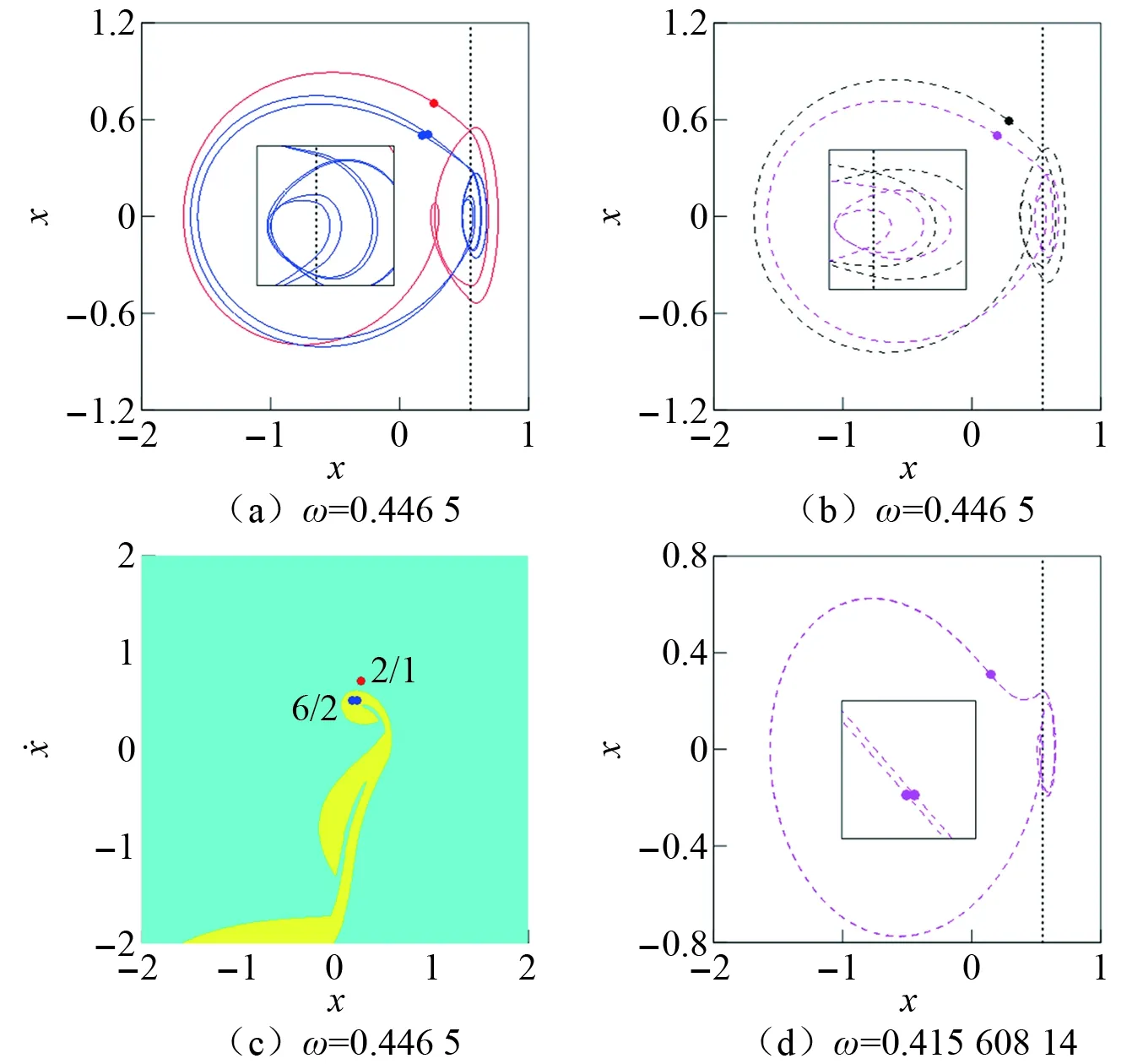
由图4(c)可知,在P1点,擦边分岔线和绿色鞍结分岔线横截相交,鞍结分岔SN2与擦边分岔GR重合,1/1与2/1运动经GR连续转迁,同时,鞍结分岔SN2产生1个新的2/1运动和1个U2/1运动。因此,P1点是二重擦边-鞍结分岔点。两条鞍结分岔线的汇交点P2为二重鞍结分岔点。图4(d)为间隙b在点P1和P2附近取值,非光滑界面Σ1的速度随ω变化的单参数分岔图。图中,0.96

由前面的分析可知,1/1运动的擦边分岔GR是连续的,但是鞍结分岔SN1的出现使系统响应在擦边邻域内不连续,引起迟滞现象。U2/1运动存在于整个迟滞域HR1和亚谐包含域SIR1内。不同的是,迟滞域内的U2/1运动由鞍结型擦边分岔产生,而亚谐包含域内的U2/1运动由周期倍化型擦边分岔产生。分岔参数继续变化,U2/1运动经鞍结或周期倍化分岔恢复2/1运动从而使系统响应退出迟滞域或亚谐包含域。

4.2 2/1与3/1运动的转迁

当p>1时,亚谐包含域SIRp出现在波浪状边界线Lp/1∩(p+1)/1的波峰处。p/1与(p+1)/1运动之间出现3种转迁方式:连续擦边分岔、迟滞域和亚谐包含域。2/1与3/1运动经迟滞域转迁的分岔图,如图6(a)所示。分岔点GR和SN1之间的距离Δω=0.000 014 63。减小ω,2/1运动的鞍结型擦边分岔GR-SN1产生向ω增大方向弯曲的U3/1运动分支,引起迟滞现象。然后增大ω,系统再次发生鞍结分岔(SN2)使U3/1运动恢复稳定。迟滞区内共存周期运动的吸引域如图6(b)所示。

图6 2/1与3/1运动经迟滞域的转迁,b=0.7Fig.6 Transition between 2/1 and 3/1 motions crossing a hysteresis region, b=0.7

亚谐包含域SIR2内的亚谐周期运动模式及其参数域,如图7(a)所示。与SIR0和SIR1内的动力学相比,SIR2内的动力学更加复杂。用图7(b)和图7(c)提供的单参数分岔图解释SIR2的形成机理及其内部亚谐周期运动的分岔。延拓打靶法计算的结果,见图7(b)。不同类型的分岔用不同颜色的圆点表示,实线表示稳定周期解,虚线表示不稳定周期解。数值计算结果见图7(c)。由图7(b)和图7(c)可知,SIR2内出现许多稳定和不稳定的周期运动及分岔点。图7(b)左侧和右侧2/1运动的分岔分别对应SIR2的左右边界,中间3/1运动的分岔对应SIR2的下边界。图7(b)的局部放大,如图8所示。结合图7和图8可知,SIR2的左边界线为2/1运动的周期倍化分岔线,右边界为两条鞍结分岔线形成的迟滞带,左下和右下边界线分别为3/1运动的亚临界和超临界周期倍化分岔线。

图7 2/1与3/1运动经亚谐包含域的转迁Fig.7 Transition between 2/1 and 3/1 motions crossing a subharmonic inclusion region

图8 图7(b)的局部放大Fig.8 Local amplifications of Fig.7(b)

由图8(a)可知,减小ω当ω=0.446 108 48(SN1)时,Floquet特征乘子为λ1=-0.184 33,λ2=1.000 10,2/1运动经鞍结分岔消失,系统响应跳跃为6/2运动。相反,当ω增大时,周期倍化分岔PD1(ω=0.446 909 20)使U3/1运动恢复稳定,然后当ω=0.448 936 13·(SN2)时,3/1运动经鞍结分岔消失,系统响应跳跃为2/1运动。鞍结分岔点SN1和SN2在2/1运动与亚谐包含域SIR2内6/2运动的分岔过程中形成迟滞区。与4.1节描述的迟滞区的形成机理不同的是,该迟滞区内没有发生稳定周期运动的擦边分岔,但发生了不稳定周期运动的擦边分岔GR1(ω=0.447 743 36),使产生于SN1点的U2/1运动与产生于SN2点的U3/1运动连续转迁。

见图8(a)迟滞区内,系统呈现多种类型的共存周期运动。在SN1和PD1之间,6/2和2/1运动及U3/1和U2/1运动共存。共存周期运动的相图和Poincaré映射图如图9(a)和图9(b)所示,稳定周期运动的吸引域如图9(c)所示。在PD1点,6/2运动和U3/1运动的轨线重合产生3/1运动。因此,在PD1和GR1之间,3/1和2/1运动及U2/1运动共存。在GR1点,U2/1运动分岔为U3/1运动,因此,在GR1和SN2之间,3/1和2/1运动及U3/1运动共存。

图9 相图、Poincaré映射和吸引域,b=0.55Fig.9 Trajectories, Poincaré maps and basins of attraction, b=0.55

亚谐包含域SIR2的左边界线为周期倍化分岔线。见图7(b)和图7(c),增大ω,2/1运动在ω=0.392 255 12(PD2)处发生周期倍化分岔。延拓追踪产生于PD2点的4/2运动,当ω=0.392 747 70(GR2)时,系统发生擦边分岔产生5/2运动。继续增大ω,5/2运动在ω=0.395 817 00(PD3)处经周期倍化分岔失去稳定性,随后在ω=0.399 150 90(PD4)处经周期倍化分岔又恢复稳定。进一步增大ω,系统响应经左下边界退出亚谐包含域SIR2,5/2运动跳跃为3/1运动,分岔细节见图8(b)。

亚谐包含域SIR2的右下边界为3/1运动的超临界周期倍化分岔线。见图7(b),增大ω,3/1运动在ω=0.426 167 30(PD6)处发生周期倍化分岔产生U3/1运动和6/2运动。U3/1运动分支连接前面介绍的PD1点。6/2运动在ω=0.434 119 5(GR5)处经擦边分岔转迁为5/2运动,然后在ω=0.439 437 40(PD7)处经周期倍化分岔失去稳定性。继续增大ω当ω=444 047 18(GR6)时,系统发生不稳定周期运动的擦边分岔由U5/2运动产生U6/2运动。U6/2运动在ω=0.445 747 75(PD8)处获得稳定。由图7(c)可知,在PD7点之后,5/2运动经交替出现的周期倍化分岔和擦边分岔产生混沌,然后经3/1运动的周期倍化序列退出混沌。

4.3 亚临界周期倍化分岔

图8(b)描述了3/1与5/2运动之间的分岔细节。减小ω当ω=0.415 587 21(PD5)时,Floquet特征乘子为λ1=-0.999 99,λ2=-0.163 07,3/1运动发生周期倍化分岔。应用延拓打靶法发现U3/1运动在ω=0.415 417 25(GR3)处转迁为U2/1运动,然后一直持续到PD2点。在PD5点,系统的稳态响应由3/1运动跳跃为5/2运动,而且存在迟滞现象。因此,PD5为亚临界周期倍化分岔。经过进一步的详细计算可知,3/1运动的周期倍化分岔PD5产生6/2运动。但是,6/2运动存在的区间Δω=0.000 000 39。当ω=0.415 586 82(SN3)时,Floquet特征乘子为λ1=1.000 01,λ2=0.026 40,鞍结分岔使6/2运动失去稳定性,产生向ω增大方向弯曲的U6/2运动。此后,增大ω,在ω=0.415 608 14(GR4)处,系统发生不稳定周期运动的擦边分岔产生U5/2运动。U6/2擦边运动的相图和Poincaré映射图如图9(d)所示。U5/2运动在ω=0.415 640 34(SN4)处经鞍结分岔获得稳定,同时恢复ω递减的变化方向。由此可见,亚临界周期倍化分岔PD5的本质是发生在周期倍化分岔极小邻域内的鞍结分岔SN3使系统响应产生跳跃和迟滞。把这种周期倍化分岔可称为鞍结型周期倍化分岔(PD5-SN3)。此外,由于迟滞区内出现不稳定周期运动的擦边分岔GR4,使得系统的稳态响应经3/1运动的鞍结型周期倍化分岔跳跃为5/2运动,而不是6/2运动,这点与常规亚临界周期倍化分岔行为不同。最后,擦边分岔GR3的发生导致U3/1运动没有存在于整个亚谐包含域SIR2内,这点与SIR0和SIR1的动力学不同。

取b=0.36,系统在ω∈[0.371,0.374]变化的分岔图如图10所示。减小ω,2/1运动的擦边分岔GR1(ω=0.372 263 82)产生3/1运动,然后经周期倍化分岔PD(ω=0.372 183 10,Floquet特征乘子为λ1=-0.131 88,λ2=-0.999 99)产生6/2运动。继续减小ω,在ω=0.372 173 58(GR2)处,6/2运动经擦边分岔转迁为5/2运动。随后在ω=0.372 153 86(SN1)处,特征乘子为λ1=0.017 39,λ2=0.999 97,5/2运动经鞍结分岔失去稳定性,产生向ω增大方向弯曲的U5/2运动。此后,增大ω,在ω=0.372 911 30(SN2)处,不稳定的U5/2运动经鞍结分岔获得稳定,同时恢复ω递减的变化方向。由此可见,亚临界周期倍化分岔PD的本质是发生在周期倍化分岔极小邻域内的鞍结型擦边分岔GR2-SN1使系统响应产生跳跃和迟滞。迟滞区内,共存的6/2运动和U5/2的相图,如图11所示。

图10 亚临界周期倍化分岔,b=0.36Fig.10 Subcritical period-doubling bifurcation, b=0.36

图11 共存运动的相图,b=0.372 18Fig.11 Trajectories of coexisting motions, b=0.372 18

5 结 论

本文考虑单自由度弹性碰撞振动系统,利用局部映射方法构建系统各类周期运动的Poincaré映射,推导了周期运动分岔分析的延拓打靶法,以及计算Floquet特征乘子的半解析法。应用数值方法辨识系统在(ω,b)参数平面的稳定周期运动模式及其参数域。基于延拓打靶法和Floquet理论分析了相邻周期1运动的分岔特征,揭示了两参数平面内迟滞域和亚谐包含域的形成机理以及二重擦边-鞍结分岔和二重鞍结分岔现象,讨论了亚临界周期倍化分岔引起系统响应跳跃及迟滞的原因。

弹性碰撞振动系统的擦边分岔是连续的。但是鞍结分岔的出现使系统响应在擦边邻域内不连续,引起迟滞现象。在p/1和(p+1)/1运动的转迁过程中,p/1运动的鞍结型擦边分岔产生迟滞域HRp,U(p+1)/1运动存在于整个迟滞域HRp内。

当p=0和1时,p/1运动的周期倍化型擦边分岔产生亚谐包含域SIRp。SIRp被(p+1)/1运动的周期倍化分岔线包围,因此,U(p+1)/1运动存在于整个亚谐包含域SIRp内。而当p>1时,亚谐包含域SIRp主要被p/1和(p+1)/1运动的周期倍化分岔线包围,因此,SIRp内存在Up/1或U(p+1)/1运动。当不稳定周期运动分支连接两个不同模式稳定周期运动分支时,必然要发生不稳定周期运动的擦边分岔。

亚临界周期倍化分岔的本质是发生在周期倍化分岔极小邻域内的鞍结分岔或鞍结型擦边分岔使系统响应产生跳跃和迟滞。与常规亚临界周期倍化分岔行为不同的是,由于迟滞区发生了稳定或不稳定周期运动的擦边分岔,使得p/n运动的鞍结型周期倍化分岔产生(2p+1)/2n或(2p-1)/2n运动,而不是2p/2n运动。