一种用于场地-建筑群体系地震响应分析的二维耦合法

2023-10-10梁建文杨晶丽

振动与冲击 2023年18期

韩冰, 梁建文, 杨晶丽

(1. 天津城建大学土木工程学院,天津 300384;2. 天津大学建筑工程学院,天津 300354)

城市地区建筑物密集,相邻建筑物之间通过下部土体联系在一起。地震作用下,首先场地的滤波放大效应会影响地震动;其次,基础周围土体的振动迫使基础产生振动,而上部结构与基础之间的相对运动又会影响基础与土体的运动;另外,振动的结构也可看做额外的波源,相邻结构之间通过土体存在着能量交换。这一复杂的场地土体、基础、结构间的相互作用过程称为结构-土-结构动力相互作用(structure-soil-structure interaction, SSSI),或场地-建筑群动力相互作用。试验研究[1]证实,相邻结构的存在会影响整个SSSI体系的动力特性,忽略SSSI效应可能低估结构的动力响应[2-3]。

目前结构-土-结构动力相互作用研究,按研究对象中所包含的建筑数量不同,可分为两类:一类是两个相邻结构与土体之间的相互作用;另一类是建筑群(3个结构及以上)与土体之间的相互作用即场地-建筑群动力相互作用或场地-城市动力相互作用。由于研究对象数量少、计算量相对较小,目前关于两相邻结构与土体之间相互作用的研究较多,研究成果采用解析法[4]或数值法[5-11]或试验法[12-13],考虑线性变形或非线性变形,考虑两相邻结构参数相同或参数不同等。文献[14-15]综述了结构-土-结构动力相互作用的研究现状。由于问题的复杂性及计算量过大,关于场地-建筑群动力相互作用的研究目前相对较少。Wong等[16]采用解析法,建立均匀场地中二维半圆形埋置刚性基础-上部结构模型,进行数值计算和分析,表明建筑群之间的相互作用是复杂且难以预料的,基础周围波的散射、衍射和干涉可能产生显著的屏蔽效应或放大效应。Murakami等[17]采用解析法,研究了周期结构之间的相互作用,发现不仅直接相邻结构之间的相互作用对结构动力响应有显著的影响,更远处结构的影响也不可忽略。Padrón等[18]采用边界元-有限元耦合法,建立三维桩基-结构群模型,研究了S波、Rayleigh波激励下结构间距离及相对位置的影响,数值分析表明,场地-建筑群相互作用可能增大也可能减小结构动力响应幅值,当结构参数相似时SSSI效应显著,S波入射时λ/2(λ波长)是结构间最不利距离。Guéguen等[19]通过一个ML=4.1震后震感调查及数值分析,证实了建筑群效应的影响。Tsogka等[20]建立二维城市(10个不同距离、不同参数的结构)-场地模型,通过数值分析表明在建筑密集地区,忽略场地-建筑群相互作用的影响是不合理的。Gueguen等[21]推导了一种解析方法,希望得到一个普适性的界限距离,超过此距离的结构可忽略其影响,但计算发现这种界限距离无法获得。Boutin等[22]采用一种解析方法评估场地-城市效应对自由场运动及基底运动的影响,分析表明场地和城市效应耦合在一起并明显影响自由场运动。Kham等[23]采用边界元法研究了地基土层与城市之间的相互作用,计算中考虑了两种二维的城市模型:一种是结构的参数相同间距也相同;另一种是两种参数的结构随机布置且间距不同。Boutin等[24-25]采用周期排列的结构模型研究了场地-城市效应。

由于问题的复杂性及计算量过大,目前大部分场地-建筑群(或场地-城市)地震响应计算模型中均采用简化的结构模型,如单质点模型和等效均质块体模型[26-27]。单质点模型或刚性基础-单质点模型具有计算量小的优点,但将实际结构等效为单质点过程中需要确定等效高度、等效刚度等参数,增大建模工作量。等效均质块体模型的优势是:模型参数简单且直观;缺点是:基础与上部结构需进行单元离散,当建筑数量较多时,将增大计算量。本文主要的研究目标是发展一种适用于场地-建筑群地震响应的计算方法:将刚性基础-等效均质块体模型的解析算法模型与FE-IBE(finite element-indirect boundary element)耦合法结合,采用解析算法计算建筑群的地震响应,这样建筑群无需离散单元,计算量小,结构参数简单直观;且保留了耦合法的优势(无需人工边界即可满足无穷远处辐射条件,可考虑场地土体的非线性变形)。在此基础上,通过数值计算,分析场地-建筑群效应对结构动力响应幅值的影响。

1 计算方法

1.1 计算模型

模型图如图1所示。一个建筑群由n个结构组成,结构高度分别为H1,H2,…,Hn,结构宽度为W1,W2,…,Wn,基础埋深为E1,E2,…,En。结构之间的距离分别为b12,…,b(n-1)n,上部结构质量与基础质量的比值分别是Mb1/M01,Mb2/M02,…,Mbn/M0n,基础质量与被基础替换掉的土的质量比值为M01/Ms1,M02/Ms2,…,M0n/Msn,假定底部固定的结构基频分别为f11,f21,…,fn1。计算中,假定基础为刚性的,上部结构用仅发生剪切变形的等效匀质块体模拟[28]。上部结构的底部固定基频为fi1,i=1,2,…,n,其泊松比νb1,νb2,…,νbn,其阻尼比为ζb1,ζb2,…,ζbn。假定场地由线弹性、各向同性、水平成层的土层及下卧弹性基岩组成,各土层及基岩可由拉梅常数λEj,Gj,泊松比νj,质量ρj,阻尼比ξj表征。地震波自基岩面以角度θ入射。

图1 模型图Fig.1 The model

1.2 耦合算法介绍

如图2所示,远场的土体用间接边界元模拟,称为间接边界元子域ΩB。近场土体用有限元模拟,称为有限元子域ΩF,ΩF的宽度和高度分别为W和H。建筑群(包括上部结构和基础)采用刚性基础-等效均质块体模型模拟,其在地震激励下的动力响应可用解析表达式求解。ΩB与ΩF之间的公共边界用SFB表示。各基础与有限元子域的公共边界用S1,S2,…,Sn表示。ΩB与ΩF通过SFB上位移连续、应力平衡边界条件耦合,建筑群与ΩF通过S1,S2,…,Sn上的位移连续条件耦合。

图2 有限元子域、间接边界元子域简图Fig.2 The model of FE and IBE subdomain

这种耦合法最大的优点在于上部结构直接采用刚性基础-等效匀质块体模型的解析表达式求解,无需离散单元,在模拟大型建筑群时,能显著降低模型的计算规模。其次,用边界元法模拟无限域场地时,可自动满足无穷远处的辐射条件,无需使用人工边界。

1.2.1 间接边界元子域计算

首先将间接边界元子域的边界SFB离散为N个单元,用sj(j=1,…,N)表示。相应的,基岩上部土层被划分为m个子层。地震激励下间接边界元子域动力响应由两部分组成,自由场响应和散射场响应。

对于自由场响应可由直接刚度法求解。首先,由各子层土体刚度矩阵[Ej](j=1,2,…,m)及基岩的刚度矩阵[ER]集整为整体刚度矩阵[EF],[Ej]及[ER]的表达式参见Han等的研究。当地震波在基岩面入射时,节点荷载矩阵 [PF]=[0,0,…,0,P2m+1,P2m+2],P2m+1和P2m+2的表达式参见Han等的研究。根据[EF]和[PF]即可确定节点位移,进而可确定间接边界元子域SFB上的位移[uf]和应力[tf]。

在此耦合法中,假定有限元子域ΩF对边界元子域ΩB的作用可通过施加在公共边界SFB上的虚拟均布荷载[PB]表示,则散射场响应是指边界元子域ΩB在[PB]作用下的动力响应。接下来计算公共边界SFB上的位移格林函数[guB]ij和应力格林函数[gtB]ij,[guB]ij和[gtB]ij代表的是单元sj(j=1,…,N)上作用单位荷载时,单元si(i=1,…,N)上的位移和应力响应,具体求解方法参见Han等的研究。

则在边界元子域ΩB上,公共边界SFB的总的位移响应[u]B和应力响应[t]B可表示为

[u]B=[uf]+[guB][PB]

(1)

[t]B=[tf]+[gtB][PB]

(2)

1.2.2 有限元子域计算

有限元子域中的土体离散为四节点等参单元。为了便于同间接边界元子域耦合,有限元子域上SFB的节点坐标与间接边界元子域SFB的节点坐标完全相同。边界S1,S2,…,Sn被分别划分为N1,…,Nn段。计算时,首先建立有限元子域整体刚度矩阵[KF],其中质量和阻尼采用的是集中质量矩阵和滞后阻尼。[KF]还可以如下形式表达

(3)

式中: 下标“s”为位于边界SFB,S1,S2,…,Sn上的节点; 下标“u”为内部节点。地震激励下,有限元子域上只有作用在公共边界SFB,S1,S2, …,Sn上的荷载[PF]={[PFB],[P1],[P2],…,[Pn]},假定荷载[PF]可以等效为作用在边界sj上幅值为pFj(j=1,…,M,M+1,…,M+N1+…+Nn)的均布荷载,则ΩF的动力响应可表示为

(4)

式中, [A]为转换矩阵,将边界单元上的均布荷载转换为节点荷载。

为便于与边界元子域耦合,在有限元子域内定义一种类似位移格林函数[guF],[gu1],[gu2],…,[gun]为在边界SFB,S1,S2, …,Sn的各单元上施加单位均布荷载后,SFB上各单元的位移响应[29-30]。相应地,[gtF],[gt1],[gt2],…,[gtn]是类似应力格林函数。则在有限元子域的SFB上,位移和应力响应可用下式表达

[u]F=[guF,gu1,gu2,…,gun][PF]T

(5)

[t]F=[gtF,gt1,gt2,…,gtn][PF]T

(6)

同样定义[gui1],[gui2],…,[guin],[guiF]为Si上的位移格林函数,则ΩF的边界S1上的位移可表示为

[u1]F=[gu1F,gu11,gu12,…,gu1n][PF]T

(7)

ΩF的边界S2上的位移可表示为

[u2]F=[gu2F,gu21,gu22,…,gu2n][PF]T

(8)

⋮

ΩF的边界Sn上的位移可表示为

[un]F=[gunF,gun1,gun2,…,gunn][PF]T

(9)

1.2.3 上部结构动力响应计算

假设作用在刚性基础边界S1,S2,…,Sn上各单元的合力向量可用[-P1], [-P2],…, [-Pn]表示,则各基础的位移向量可由下式表达

[u1]A=[w1][ω2(M01+Mb1)]-1[w1]T[-P1]

(10)

[u2]A=[w2][ω2(M02+Mb2)]-1[w2]T[-P2]

(11)

⋮

[un]A=[wn][ω2(M0n+Mbn)]-1[wn]T[-Pn]

(12)

[Δi]=[ω2(M0i+Mbi)]-1[wi]T[-Pi]

(13)

结构顶部水平向和竖向的绝对位移可表达为

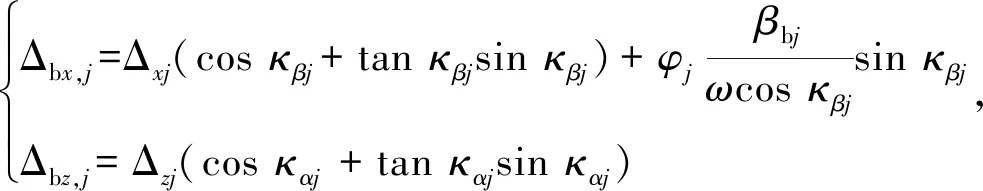
(14)

1.2.4 边界耦合条件

边界SFB上的位移连续条件为

[guB][PB]>+>[uf]=>[guF,gu1,gu2,…,gun][PF]T

(15)

边界SFB上的应力平衡条件为

[gtB][PB]+[tf]+
[gtF,gt1,gt2,…,gtn][PF]T=0

(16)

S1上的位移连续条件为

[gu1F,gu11,gu12,…,gu1n][PF]T=
[w1][ω2M1]-1[w1]T[-P1]

(17)

S2上的位移连续条件为

[gu2F,gu21,gu22,…,gu2n][PF]T=
[w2][ω2M2]-1[w2]T[-P2]

(18)

⋮

Sn上的位移连续条件为

[gunF,gun1,gun2,…,gunn][PF]T=
[wn][ω2Mn]-1[wn]T[-Pn]

(19)

式(17)可以变形为

[gu1F][PF]=
-[C1,gu12,…,gu1n][P1,P2,…,Pn]T

(20)

式中,[C1]=[gu11]+[w1][ω2M1]-1[w1]T。同样式(18)可以变形为

[gu2F][PF]=

-[gu21,C2,gu23,…,gu2n][P1,P2,…,Pn]T

(21)

式中,[C2]=[gu22]+[w2][ω2M2]-1[w2]T。

⋮

同样,式(19)可以变形为

[gunF][PF]=

-[gun1,gun2,…,gun(n-1),Cn][P1,P2,…,Pn]T

(22)

式中,[Cn]={[gun]+[wn][ω2Mn]-1[wn]T}。然后,[PF]和[Pi],i=1,2,…,n的关系可联立式(20)～式(22)解得

[Pi]=[Di][PF],i=1,2,…,n

(23)

将式(23)代入式(20)～式(22)可得

[guB][PB]+[uf]={[guF]+[gu1][D1]+
[gu2][D2]+…+[gun][Dn]}[PF]

(24)

[gtB][PB]+[tf]+[gtF][PF]+{[gt1][D1]+
[gt2][D2]+…+[gtn][Dn]}[PF]=0

(25)

式(24)和式(25)联立即可解得作用在公共边界SFB上的虚拟荷载[PB]和[PF]相应地[Pi],i=1,2,…,n可通过式(23)和[PF]求得,则结构的动力响应通过式(10)～式(14)可以求得。

2 精度验证

为验证这种耦合法的正确性及计算精度,一组本文耦合法计算结果与Liang等研究的中间接边界元法计算结果对比,如图3所示。图3(a)计算参数: 结构间距离D/W1=2(D/a=4[6]),基岩与土层刚度比βR/βL=2,场地阻尼比ζR=ζL=3.5%,场地泊松比νR=νL=1/3,结构宽度W1=W2=2a,结构高度H1=H2=2W1=4a,上部结构质量与基础质量的比Mb/M0=5,基础质量与被基础替换掉的土体的质量比M0/Ms=0.2。图3(b)中βR/βL=5,其他参数与图3(a)相同。计算参数如下,两个相同的刚性基础半径为a=W1/2,W1为结构宽度,结构间距离b/W1=2,上部结构高度H1=H2=2W1=4a,上部结构与基础质量比Mb/M0=5,基础与之替换掉的土的质量比M0/Ms=0.2。基岩上部土层等效为单层土,土层厚度D/W1=2,基岩和土层阻尼比ζR=ζL=3.5%, 基岩和土层泊松比νR=νL=1/3, 基岩和土层剪切波速比分别取为βR/βL=2 和βR/βL=5。Δi为基础水平向位移与入射波幅值的比值(无量纲); Δbi为结构顶部水平向相对位移与入射波幅值的比值(无量纲)。如图3所示,两种方法的计算结果吻合较好,说明本文发展的这种有限元-间接边界元耦合法计算准确,精度可靠。

图3 本文耦合法计算结果与Liang等研究的间接边界元法计算结果(IBEM)对比Fig.3 Comparison of our results for twin buildings supported by semi-circular rigid foundations with those obtained by indirect boundary element method in linear range of research on Liang et al

另外,为验证本文耦合法在计算建筑群(多个结构)地震响应的计算精度,一组本文耦合法计算结果与边界元方法结果的对比,如图4所示。其中建筑群包括5个相同结构,结构高度21 m,结构宽度25 m,等效均质块体结构模型泊松比1/3,结构基频1.25 Hz,基础为半圆形刚性基础,基础质量与被基础替换掉的土体的质量比是M0i/Msi=0.2,上部结构质量与基础质量的比值是Mbi/M0i=5,结构间距离均为40 m;均匀场地参数为剪切波速200 m/s,质量密度2 000 kg/m3,泊松比0.33。入射波为峰值加速度0.1g的Taft波。边界元法的结果采用Han等研究的方法,可以看出本文耦合法计算结果与边界元方法结果吻合较好。

围观之人被带起的如冰碴般的气流刮得肌肤生痛。萧飞羽跨前一步双掌猛然上扬迅速拍出。“啪！啪！啪……”一阵响声过后双方各后退三步。

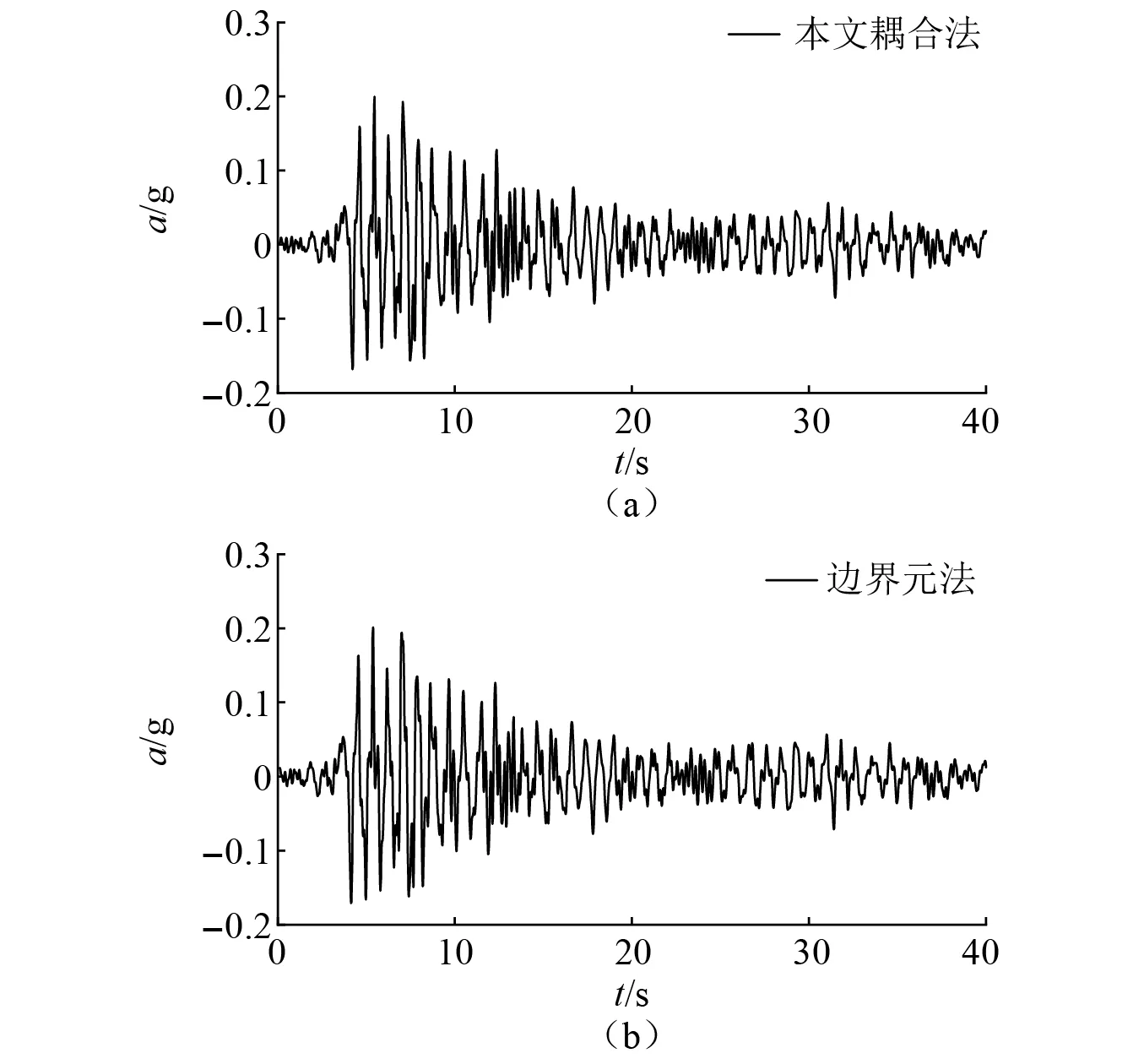
图4 本文耦合法计算结果与Han等研究的边界元法计算结果对比Fig.4 Comparison of our results for seismic response of site-buildings interaction with those obtained by boundary element method in research on Han et al

但需要指出,Liang等和Han等研究的方法适用于半圆形刚性基础;当建筑群中结构数量较多时,计算过程非常复杂;尤其当建筑群中各结构(基础)差别较大时,计算难度大。而本文发展的耦合法在上述问题中显示出明显优势,因此更适用于场地-建筑群地震响应计算。

3 数值计算与分析

以5个6层的框架结构和(或)11层框架结构组成的建筑群进行算例分析。算例分析分为两部分,每部分对8组算例进行对比分析。

6层的框架结构,结构高度21 m, 结构宽度25 m,泊松比1/3,底部固定基频1.25 Hz,基础埋深2 m,基础质量与被基础替换掉的土体的质量比是M0i/Msi=0.2,上部结构质量与基础质量的比值是Mbi/M0i=5。

11层框架结构,高度42 m, 宽度25 m,泊松比1/3,底部固定基频0.75 Hz,基础埋深4 m,基础质量与被基础替换掉的土体的质量比是M0i/Msi=0.2,上部结构质量与基础质量的比值是Mbi/M0i=10。

场地各土层的泊松比νi=1/3 (i=1～9),滞后阻尼比ξi=0.035 (i=1～9),土层其他参数如表1所示。

第一部分数值计算中入射波为峰值加速度0.1g的Taft波,结构间距离均bi=25 m,(i=1,4);第二部分数值计算中入射波为峰值加速度0.1g的El Centro 波,结构间距离均为bi=35 m,(i=1,4)。Taft 波和El Centro 波加速度时程曲线如图5所示,均从基岩面垂直入射。

图5 Taft 波和El Centro 波加速度时程曲线Fig.5 The time history of incident earthquake waves

算例(1)中,5个结构均为6层(21 m)的框架结构;算例(2)中,5个结构均为11层(42 m)的框架结构;算例(3)中,结构1～3为6层的框架结构,结构4和结构5是11层的框架结构;算例(4)中,结构1～3为11层的框架结构,结构4和结构5是6层的框架结构;算例(5)中,结构1、结构2、结构4为11层的框架结构,结构3和结构5是6层的框架结构;算例(6)中,结构1、结构2、结构4为6层的框架结构,结构3和结构5是11层的框架结构;算例(7)中,结构1、结构4、结构5为6层的框架结构,结构2和结构3是11层的框架结构;算例(8)中,结构1、结构4、结构5为11层的框架结构,结构2和结构3是6层的框架结构。算例(1)～(8)结构布置简图及结构顶部绝对加速度时程曲线如图6～图13所示,为分析周围建筑结构的影响,图中还给出相应的仅考虑土-单体结构动力相互作用(soil-structure interaction,SSI)的结果作为参考,并在图中(括号)标出了结构1～结构5加速度峰值及相对于单体结构的放大倍数。为方便对比8组算例中场地-建筑群效应对各结构顶部绝对加速度峰值的影响程度,汇总整理了图6～图13中各结构的加速度峰值相对于单体结构的放大倍数,如表2所示。

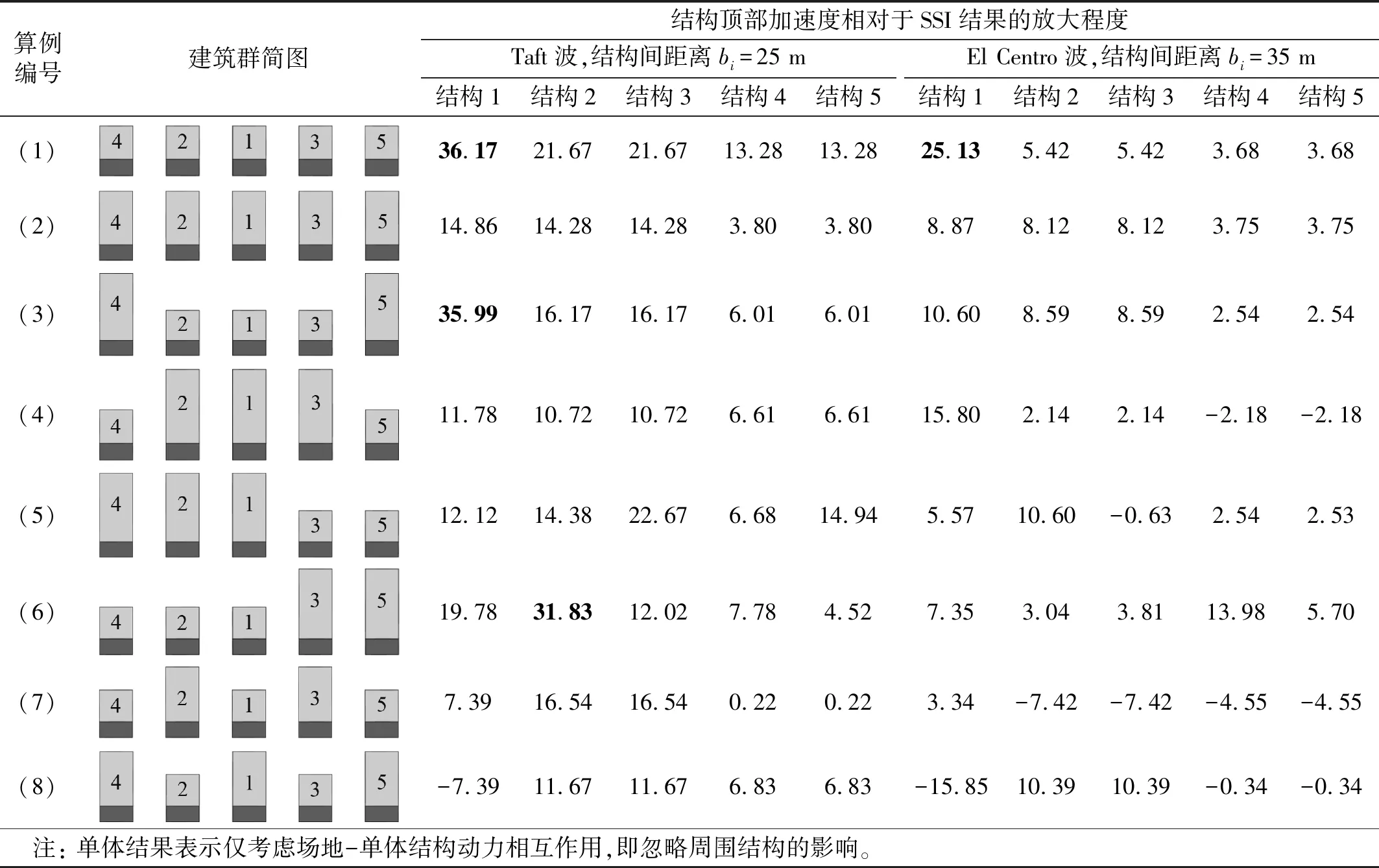
表2 算例(1)～(8)建筑群简图及结构1～结构5顶部绝对加速度峰值相对于单体结构结果的放大程度

图6 算例(1)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.6 Absolute acceleration time history on the top of the buildings in Case 1 compared with SSI result of a single building

由图6及表2可知,当建筑群中各结构参数相同时,场地-建筑群效应对结构动力响应可能有显著的影响,尤其对中心位置结构(结构1)的影响较大。在算例(1)Taft波入射时,中心位置结构(结构1)与仅考虑SSI的结果相比放大了36.17%,El Centro波入射时放大了25.13%;次中心位置结构(结构2/结构3)放大了21.67%和5.42%;对边缘位置的结构(结构4/结构5)影响较小,放大了13.28%和3.68%。

算例(2)与算例(1)规律一致,但场地-建筑群效应的影响程度明显减小,图7中当Taft波和El Centro波入射时中心位置(结构1)结构顶部绝对加速度峰值放大分别为14.86%和8.87%。这也说明,结构自身动力特性是影响场地-建筑群效应的关键因素之一,当建筑群中结构的刚度较大时,场地-建筑群效应对结构地震响应幅值的影响程度可能更大。

图7 算例(2)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.7 Absolute acceleration time history on the top of the buildings in Case 2 compared with SSI result of a single building

由图8～图11(算例(3)～算例(6))可知,当建筑群将相同参数结构分区布置(如多层区、高层区)时,场地-建筑群效应可能对各区中心位置结构的地震响应幅值的影响较大,尤其对刚度较大的结构。

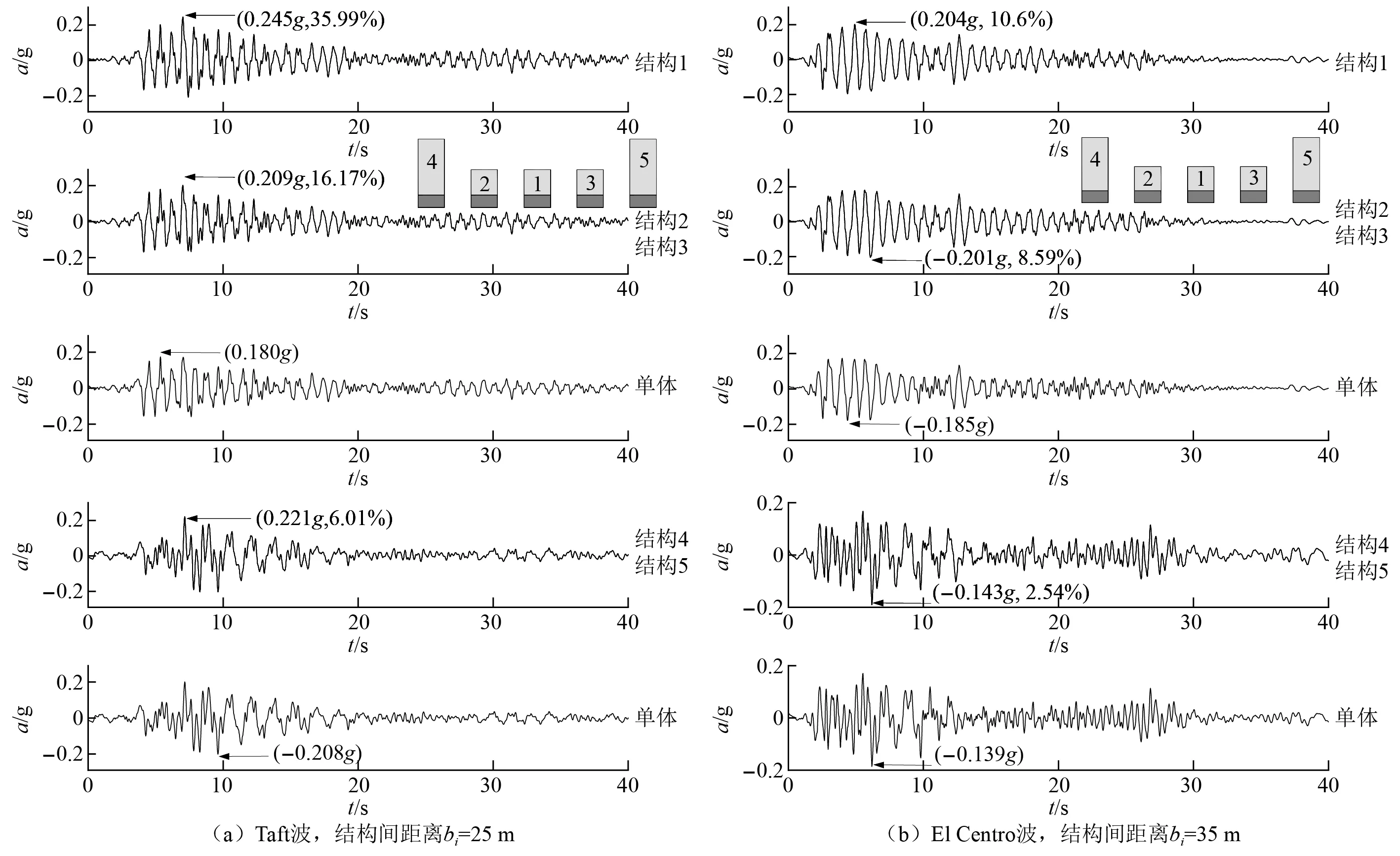
图8 算例(3)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.8 Absolute acceleration time history on the top of the buildings in Case 3 compared with SSI result of a single building

图9 算例(4)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.9 Absolute acceleration time history on the top of the buildings in Case 4 compared with SSI result of a single building

图10 算例(5)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.10 Absolute acceleration time history on the top of the buildings in Case 5 compared with SSI result of a single building

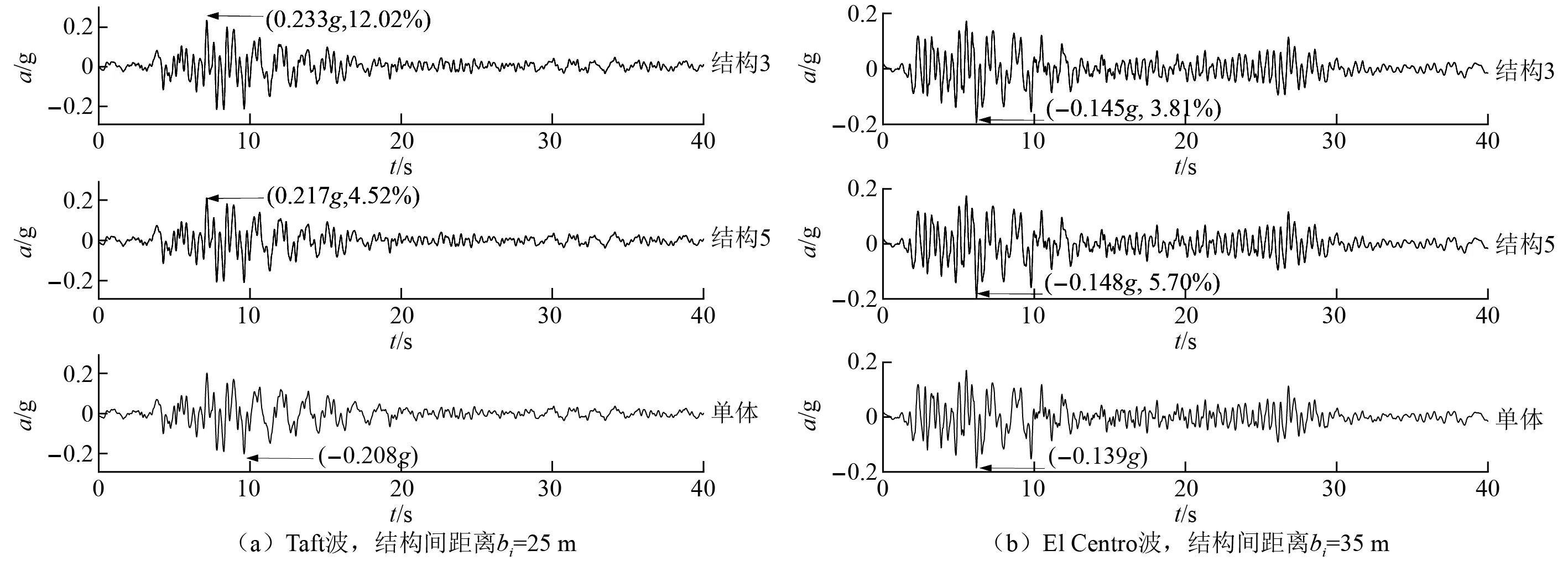
图11 算例(6)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.11 Absolute acceleration time history on the top of buildings in Case 6 compared with SSI result of a single building

如图12和图13所示(算例(7)和(8)),当建筑群中不同参数的结构交错布置时,场地-建筑群效应对结构顶部绝对加速度的放大作用相对较小,且往往不是对中心位置的结构影响最大。

图12 算例(7)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.12 Absolute acceleration time history on the top of buildings in Case 7 compared with SSI result of a single building

图13 算例(8)中结构1～结构5顶部绝对加速度时程及相应单体结构顶部绝对加速度时程Fig.13 Absolute acceleration time history on the top of buildings in Case 8 compared with SSI result of a single building

另外,综合算例(1)～算例(8)结果可以看出,场地-建筑群效应对结构动力响应的影响,与结构自身动力特性、目标结构在建筑群中的位置、建筑群布置方式、结构之间的距离、场地特性等整个场地-建筑群的特性及地震波特性相关[31]。