基于控制障碍函数的飞行器避障与制导控制
2023-10-07杜宏宝王正杰唐礼喜张小宁
杜宏宝, 王正杰, 唐礼喜, 张小宁
(北京理工大学 机电学院, 北京 100081)
0 引言
现代战争的形式更加复杂,尤其体现在城市战中,充满了建筑、车辆和行人等[1-3]。在俄乌冲突的城市攻防战中,巡飞弹等制导弹药被大量使用,例如“见证者-136”和“弹簧刀”系列都起到了重要作用,但一方面由于复杂的城市环境难以实施有效打击,另一方面打击过程难免损毁重要文物或者伤及无辜。由此可见,战场环境的复杂化和动态化对未来飞行器制导技术的发展提出了新的挑战与要求,发展能够避障的制导技术具有重要意义。为了提高低马赫制导武器在障碍物环境的适用性,有必要研究飞行器的避障与制导问题,以避开静态及动态物体的同时能够击中目标,实现绕射打击。
关于避障与制导问题,目前国内外的相关研究基于不同理论,如基于流函数法[4-7]、基于路径搜索方法[8-15]、基于人工势场法[16-18]、基于最优控制理论[19-20]以及基于控制障碍函数(CBF)的方法[21-24]等。文献[6]基于流函数的思想发展了扩展动态系统调制法,能够实时避开运动障碍物,但由于是对障碍物附近的速度场调制求解,具有一定的短视性,且难以进一步推广到具有高维动力学约束的情形。文献[9]研究了针对静态障碍物的避障制导问题,基于改进快速扩展随机树(RRT*)路径搜索方法,在实现躲避障碍物的同时打击目标,先搜索路径再作轨迹跟踪。与之类似的还有文献[10-15],均是基于路径搜索类避障方法,通常需要机载计算机规划出一条可行轨迹。这类方法由于计算复杂度高、实时性差,不适用于躲避运动障碍物的情形。文献[16] 基于人工势场法,通过构建关于空间位置及相对速度的势函数,引入引力和斥力的虚拟力概念来驱动运动体避开障碍物到达目标,但存在较大的输入震荡,且这类方法存在局部最小问题,需要通过人工干预摄动地解决;或需要对全局势场进行优化设计,通常不具备实时性[17-18]。文献[20]从弹障与弹目运动学模型出发,基于最优控制理论推导出避障制导律,具有很好的实时性。文献[21]基于CBF实现了无人艇的避障,解决了CBF在高阶系统设计困难的问题[22]。文献[20-21]的不足之处是只处理了静态障碍物,未考虑运动障碍物情形。CBF具有良好的拓展空间,文献[22]综述了近年来关于CBF的理论发展与技术应用。
综上所述,从现有研究文献可以看出,一类方法采用轨迹规划实现运动体的避障[8-15,23],由于实时性差,不适用于飞行器在动态障碍物环境的避障制导问题;另一类方法属于局部反应式的避障方法[4-6,16-21],通常是在障碍物附近作大过载机动动作避开障碍物,具有短视的缺点,因此全局性差,或没有解决动态障碍物和运动目标情况[25-30]。
本文针对运动障碍物及机动目标情形飞行器的避障制导问题,旨在发展一种具有实时性、普适性与全局性的控制方法。本文的创新点概括如下:
1)提出的控制方法同时实现了针对运动障碍物及机动目标情形的避障与制导,以飞行器与目标及障碍物的相对运动关系作为系统状态进行反馈,研究一种控制律来节省计算资源,提高了避障制导的实时性。
2)提出的避障制导控制方法在飞行器与障碍物、飞行器与目标的相对运动关系基础上,采用速度障碍法构建有效的CBF,并结合现有的比例制导律[31-32]设计了避障制导律。由飞行器与障碍的相对运动关系构建二次优化约束,避免了CBF在高阶系统的设计困难;同时可以与其他成熟制导律结合,从而实现动态和静态避障,具有普适性。
3)提出的避障制导控制方法以飞行器与障碍物的相对速度作为状态进行反馈,从而对飞行器与障碍物的相对位置具有预判能力,避免了临近障碍物时飞行器突然执行避障动作、轨迹突变的情形,飞行器饱和过载占比小,弹道轨迹平滑,具有良好的全局性。
1 飞行器-障碍物与飞行器-目标运动学模型
1.1 飞行器-障碍物运动学模型
图1所示为飞行器与障碍物的相对运动关系。图1中,OXY为惯性坐标系,M为飞行器,Obs为障碍物,d为弹障距离,v和a分别表示飞行器速度与加速度,vo表示障碍物速度,θ表示弹障视线角,σ和σo分别表示飞行器弹道角与障碍物的运动方向。由图1可知,弹障间距离变化率与弹障视线角变化率满足式(1)和式(2)关系。避障过程中通过改变飞行器弹道角方向,使得弹障间距大于安全距离,实现避障。
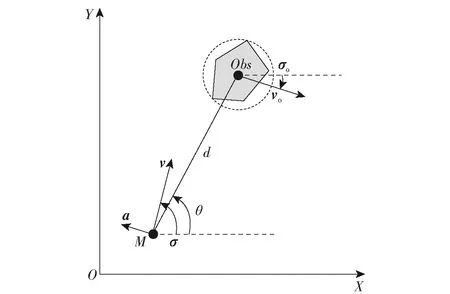
图1 飞行器与障碍物相对运动关系
(1)
(2)
1.2 飞行器-目标运动学模型
如图2所示,T为目标,r为弹目距离,vt表示目标速度,σt表示目标运动的方向角,q表示弹目视线角。制导的过程即通过改变飞行器法向过载来保证飞行器能够击中目标。
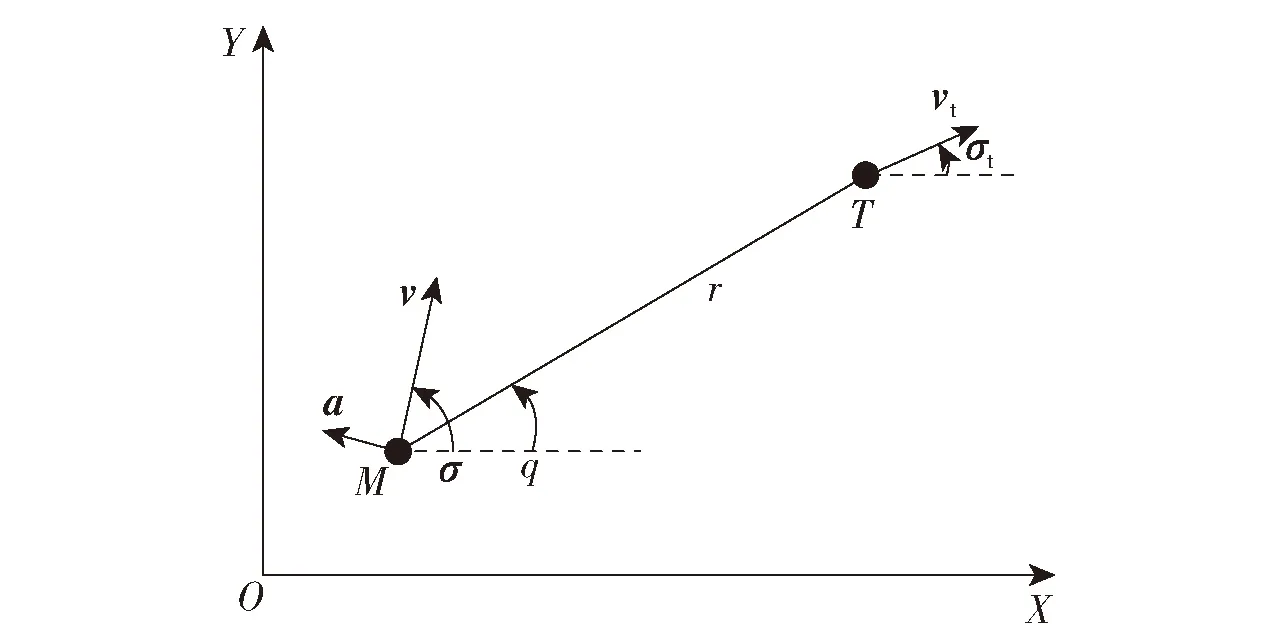
图2 飞行器与目标相对运动关系
由图2可知,飞行器与目标的相对运动关系满足式(3)~式(5):
(3)
(4)
(5)
式中:f为气动扰动。
为了便于加入避障约束,将式(3)~式(5)表示成仿射系统形式如式(6),f暂且忽略不考虑。其中,系统状态变量为x=[r,q,σ]T,飞行器法向过载a为制导控制输入。
(6)
2 避障与制导方法研究
2.1 控制障碍函数
CBF是类似于控制Lyapunov函数(CLF)的一类方法,通过求解控制律来改变系统的轨迹,使得系统状态避开空间中的某个区域或者趋近于一个平衡状态[22,24]。考虑一般的非线性系统仿射形式如式(7),x∈X为系统状态变量,X为系统状态空间,u∈U为系统的控制输入,U为系统输入空间。系统能否安全地运行,由能否构造一个可行的系统输入空间、使得系统状态轨迹在安全状态空间内所决定。
(7)
式中:f(x)为表示系统自然状态的非线性函数;g(x)表示与控制输入相关的非线性函数。
CBF方法与CLF类似,由控制系统的状态变量所构建,以实现系统状态运行在安全的状态空间内。在CLF中,V(x):D⊂Rn→R(R为实数空间,n为系统状态空间维度)是Lyapunov函数,如果存在控制输入u=k(x)满足式(8),则可以保证系统稳定性并且指数收敛于某一状态。
(8)
与CLF不同,CBF的设计是为了找到控制输入,能够使系统状态保持在安全不变集合内。控制障碍函数B(x)的定义通常满足式(9)~式(12):
B(x):D⊂Rn→R
(9)
C={x∈D⊂Rn:B(x)≥0}
(10)
∂C={x∈D⊂Rn:B(x)=0}
(11)
IntC={x∈D⊂Rn:B(x)>0}
(12)
式中:D表示控制障碍函数的定义域;C表示安全状态空间;∂C表示安全状态空间的边界;IntC表示空间内部。
系统状态变量保持在C内即保证了系统的安全。为了使系统状态在安全可行集内,系统控制输入u=k(x)需要满足式(13)和式(14):
(13)
(14)
式中:α表示K类函数;Lf、Lg分别为李导数算子关于f(x)和g(x)的表示。
CBF的应用通常是与标称控制器构建二次优化问题,既保证系统稳定的同时又保证控制系统安全运行。式(15)即为有约束二次优化问题,un表示标称控制输入,H为正定矩阵。但由于系统的相对度大于1,即系统输出与控制输入间的最小积分器个数大于1,式(14)中LgB(x)恒为0,B(x)是无效的控制障碍函数,因此构建适用于制导控制系统的控制障碍函数具有重要意义。
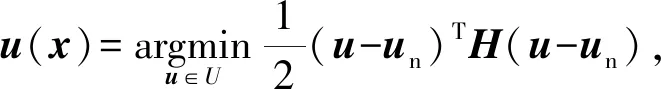
(15)
2.2 避障制导律

(16)
式中:ro为安全距离。
为构建有效的CBF,引入速度障碍法[25-28],使得CBF中包含弹障速度信息。如图3所示,灰色阴影区域为速度障碍空间,速度障碍法的核心概念是运动体与障碍物的相对速度矢量不落入速度障碍空间。
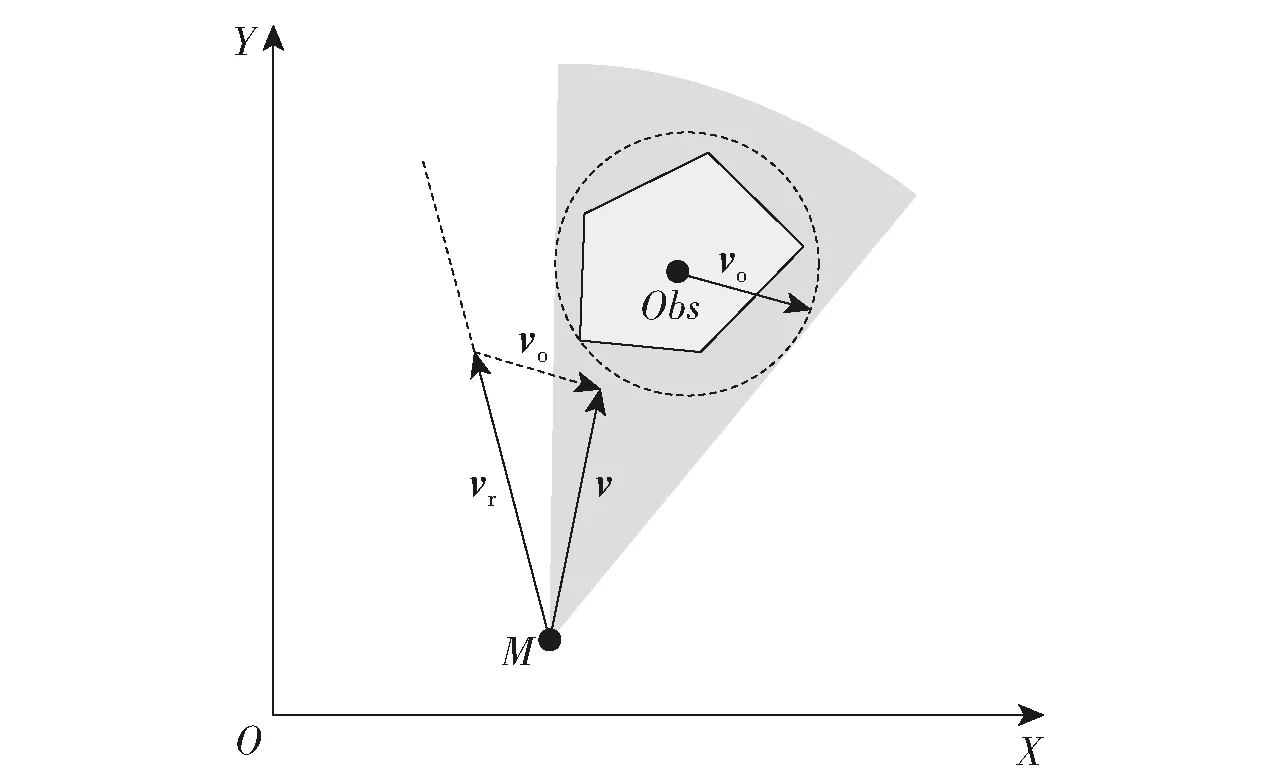
图3 速度障碍法示意图
因此,只需保证弹障相对速度矢量不落入潜在的碰撞空间内,即在未来时刻不会碰到障碍物。式(17)是本文构建的有效控制障碍函数,
(17)
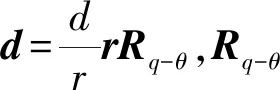
(18)
(19)
(20)
(21)
将式(4)、式(18)~式(21)代入式(17),可以得到式(22),对式(22)求李导数,由于LfB(x)=0,代入式(5)可得到式(23)。
(22)
(23)
式(22)和式(23)中的弹障距离d可通过巡飞弹激光测距仪获取[33];弹道倾角、障碍物速度及方向可通过巡飞弹自身定位及探测的环境信息状态估计得到。本文应用工程上成熟的比例制导律,如式(24)所示:
(24)

结合比例制导律,由式(22)~式(24)构建二次优化问题,如式(25):

(25)
式中:A为飞行器可行过载集,优化解即在A中求解最优避障制导律;β为安全系数。
式(25)的二次优化问题具有明确的物理意义,表示满足约束的区间内,与比例制导律取值最接近的法向过载。在式(6)系统中LfB(x)=0,由优化约束构成的区间最终可表示为LgB(x)a≥-βB(x)。利用KKT条件,当约束条件起作用时,a*=asafe表示为式(26),因此其闭式解较容易得到,式(27)即为最终避障制导律形式,避障制导律由比例制导项与避障项组成。通过引入速度障碍法的相对速度约束构造控制障碍函数,可以很好地解决原CBF的局限性[22]。
(26)
(27)
图4所示为本文飞行器避障制导律的流程框图,通过传感器获取障碍物与目标的位置与速度信息,解算出与飞行器的相对运动信息作为避障制导律的必要信息。通过构造以比例制导律为标称控制输入的二次优化问题,以基于CBF的不等式为约束,求取使得飞行器能够避障且不偏离目标的横向过载。自动驾驶仪根据所得横向过载指令发送给飞行器,以实现位置的控制。
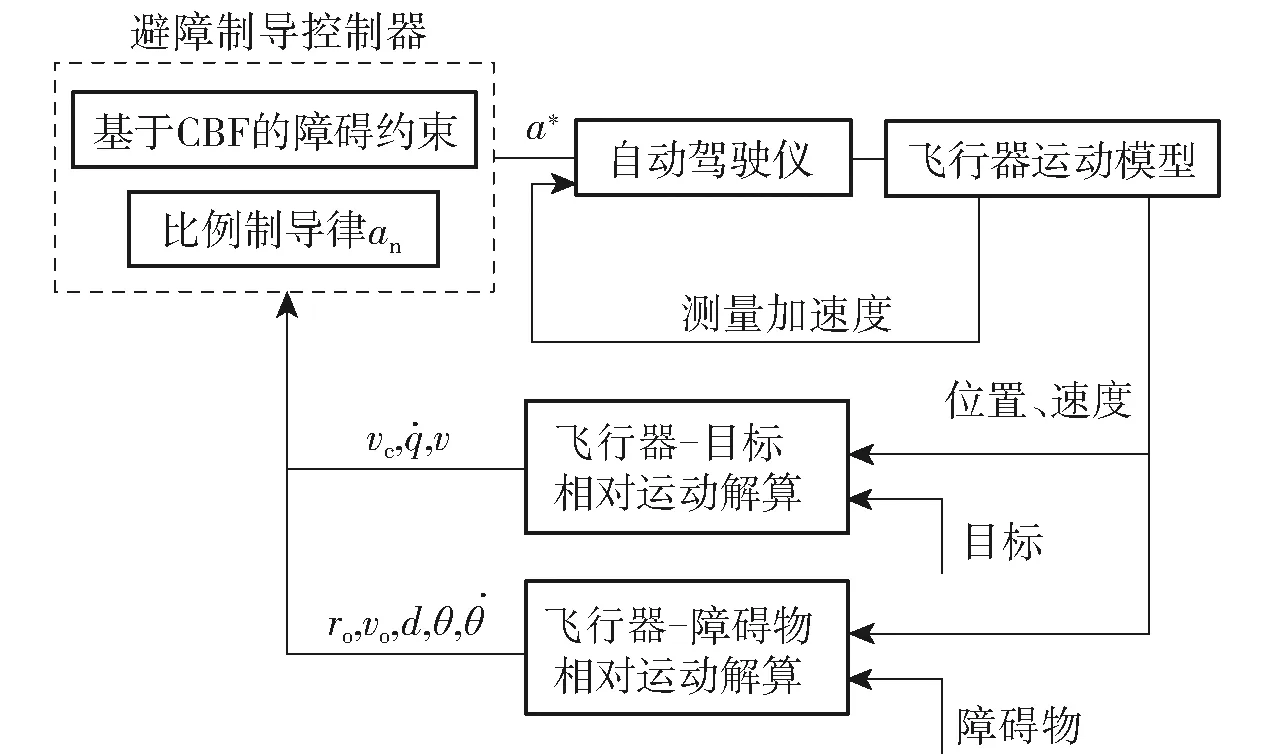
图4 飞行器避障制导控制流程
避障制导律的稳定性分析可由避障阶段与制导阶段来分析,即避障制导律中比例制导项与避障项,采用Lyapunov直接法分析,构造Lyapunov函数如式(28):
(28)
(29)
将式(3)、式(4)两式求导并代入式(29),可得到式(30):
(30)
(31)
比例制导项稳定条件是N′>2,考虑式(27)表示的避障制导律,避障项导致局部不稳定,在制导过程的全局稳定性取决于比例制导项。因此全局稳定的条件是比例制导律基础上满足平衡点不在障碍空间内,即制导结束时刻目标不在障碍空间内部。
3 数值仿真与结果分析
为验证本文避障制导律的性能,针对不同工况进行数值仿真分析。首先比较比例制导律与避障制导律,验证避障制导律的有效性;其次模拟避障制导律在障碍物尺度不同、障碍物速度不同以及目标速度不同的情况下,分析避障制导律的运动特性与动力特性,总结轨迹与过载变化规律及适用范围。此外,考虑到避障制导律在工程中的诸多扰动因素,比较不同β值的弹道轨迹特点,可通过调节β以适应实际应用。最后预设飞行器最大可行过载为9g,与文献[6]和文献[20]中的避障制导律进行性能比较。
3.1 不同条件避障制导仿真
为了验证本文提出避障制导律的有效性,对不同工况进行数值仿真分析。仿真条件的选择是考虑到障碍物对制导过程确实有影响来设计的,障碍物速度低于10 m/s时,飞行器很容易避开障碍物;障碍物速度大于50 m/s时,则对飞行器的影响时间很短,弹道轨迹几乎是比例制导律的轨迹。目标速度选择在130 m/s附近时,障碍物会对飞行器制导有影响。因此仿真基本参数选定如表1所示,飞行器速度是定值,目标速度与障碍物速度在一个范围变动,目标机动过载为1g,比例制导律的比例导引系数N′=5。图5为无避障能力的比例制导律仿真结果,障碍物由左向右以20 m/s的速度运动,目标以130 m/s的速度匀速向右偏转。虚线段为预期飞行器与障碍物的轨迹,最终飞行器在打击目标过程中撞到障碍物,打击目标任务失败。

表1 避障制导律仿真参数
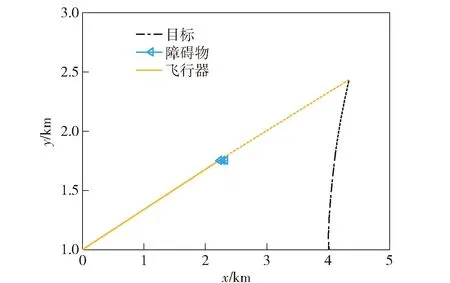
图5 比例制导律的弹道轨迹
图6(a)所示为本文提出的避障制导律在障碍物尺度不同的情形下的弹道轨迹对比,仿真参数与图5相同,对比发现避障制导律的有效性。从图6(a) 中可见,随着障碍物尺度的增大,避障制导轨迹也与预想的一样需要绕更大的弯路,整个制导任务时间增加,更早地执行避障机动。图6(b)所示为障碍物不同运动速度下的弹道轨迹对照,障碍物半径为 40 m,障碍物速度选取10~50 m/s之间的5种工况,障碍物依然从右向左运动。为便于展示区分障碍物的运动轨迹不同,赋予障碍物0.5g的顺时针机动。从图6中可以看出,避障制导律的轨迹不随障碍物速度增大而绕远,当障碍物速度达到30 m/s时,飞行器从障碍物后方经过,制导时间相比10 m/s和 20 m/s 更短。由于速度更快,相应的障碍物对飞行器的影响时间更短;障碍物速度在40 m/s和 50 m/s 时,飞行器的轨迹更短,并且几乎重合。
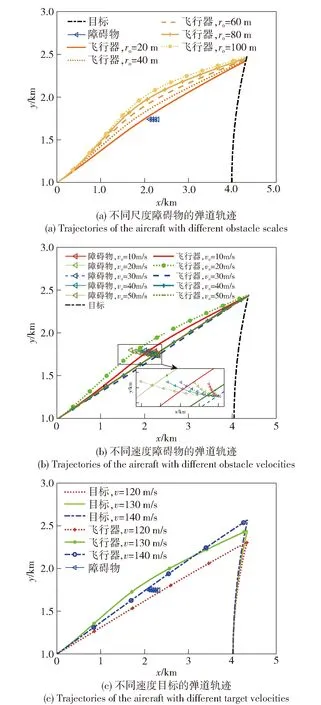
图6 避障制导律的不同工况下弹道轨迹对比
图6(c)所示为目标运动速度不同的避障制导轨迹,障碍物半径为40 m。从图6(c)中可见:目标速度较小时弹目视线之间不受障碍物影响,如目标运动速度120 m/s时,飞行器从障碍物后方经过;当目标运动在130 m/s时,障碍物的影响导致弹道轨迹较弯曲;当目标运动速度增大到140 m/s时,弹目视线角的增大使得障碍物对飞行器影响较小,因此弹道更直。综合上述仿真与分析可知,飞行器根据障碍物运动方向实时的执行机动动作,能够自主抉择从障碍物的前方或后方经过,由此可知本文提出的避障制导律具有良好的实时性与全局性。
由于飞行器在实际飞行中受气动扰动等因素,考虑式(5)的扰动项f为小于1g/v的随机扰动,可通过调节安全系数实现避障过程的抗扰能力。图7所示为不同安全系数的弹道轨迹对比,从中可见β越大、飞行器避障过程与障碍物距离越远,反之飞行器距离障碍物越近。通过改变β来改变式(25)所示的优化约束方程,增大β,可以对障碍空间进行膨胀,保证避障过程的安全性。
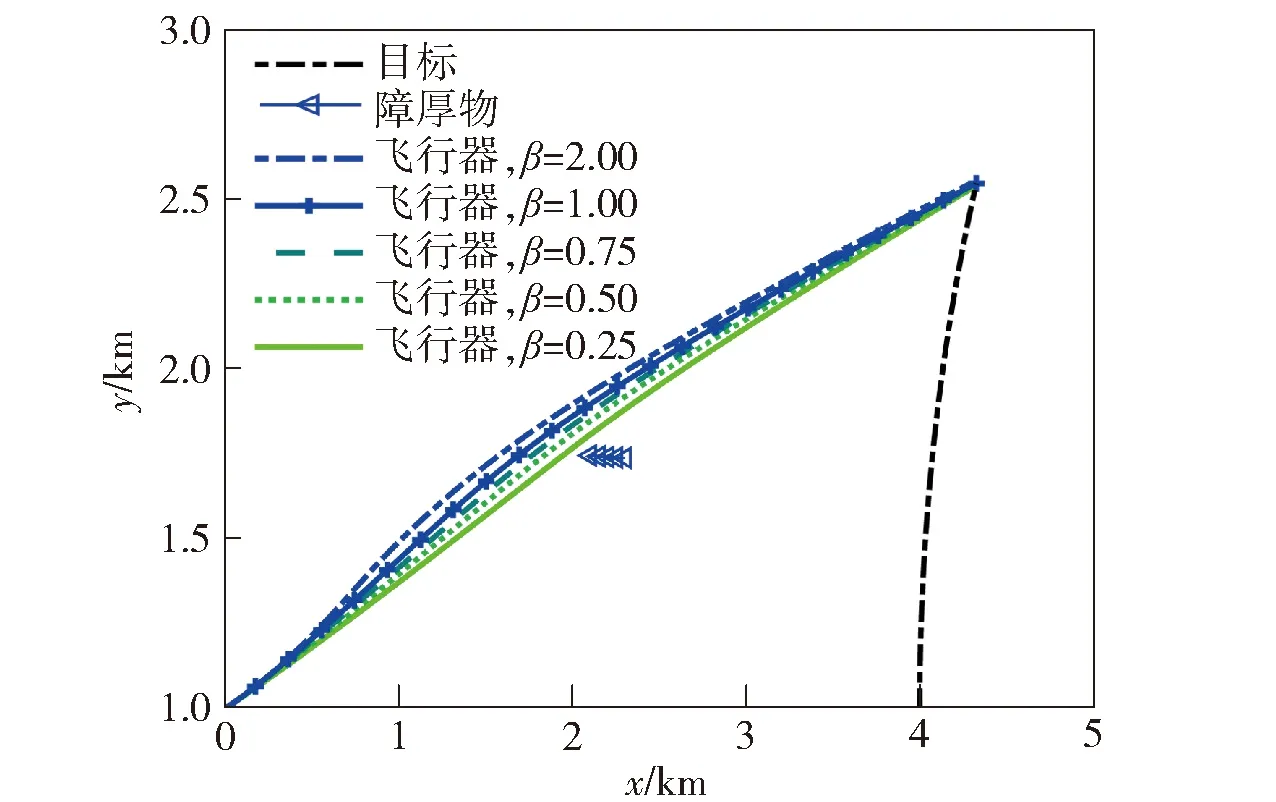
图7 不同β值的弹道轨迹
3.2 过载分析
在避障制导律的弹道轨迹特性基础上,进一步研究其过载特性。图8(a)、图8(b)所示分别为不同障碍物尺度与障碍物速度下的飞行器过载曲线。由图8(a)所示一簇曲线能够很清楚地看出避障制导律的机动特性,其中比例制导律与避障制导律的过载曲线在完成避障任务时汇于一条曲线,此时避障过载的分量为0g,仅需要执行制导任务。由于不执行避障控制,比例制导律在初始时刻的过载为0g; 避障制导律初始过载大小依据障碍物的初始位置与大小决定。障碍物半径为20 m和40 m时,初始机动过载分别为1.3g和5.8g;障碍物尺度增大到60 m后,初始即达到饱和机动过载。随后随着障碍物尺度增大,飞行器需要持续更长时间的饱和过载来避开障碍物。

图8 飞行器过载在不同工况下的法向过载对比
在图8(b)中,随着障碍物速度的变化,飞行器过载曲线具有较大的差异。其中:飞行器速度在10 m/s 和20 m/s时,过载曲线的变化趋势相近,均先减后增,与图8(a)所示更接近;障碍物速度30 m/s 时过载曲线先增后减,对应3.1节图6(b)的轨迹可以发现,飞行器从障碍物后方绕过;障碍物速度为40 m/s和50 m/s时,意味着障碍物对飞行器影响的时间窗口更小,因此最大过载不超过0.2g,障碍物速度更大时飞行器过载曲线几乎重合。图8(c) 是对应图6(c)弹道轨迹的飞行器过载曲线,从中可见当目标速度为120 m/s和140 m/s 时,弹目视线角分别从障碍物后方与前方经过,弹道弧度小,受障碍物影响小;目标速度为折中的130 m/s时,障碍物对制导过程影响较大,需要飞行器更大的初始过载及过载变化,打击目标的同时避开障碍物。
综合图8分析结果可以看出,不同工况下的避障制导律均是在比例制导过载曲线的基础上做出的改变,本文提出的避障制导律由比例制导律构建,但不局限于比例制导律,可结合其他制导律实现避障,因此具有普适性。
为探究避障制导律的适用范围,大量仿真发现飞行器避障能力与飞行器机动能力密切相关,随着可用横向过载增大,飞行器能够避开移动速度更快、尺度更大的障碍物。图9所示为飞行器速度及横向过载与障碍物速度关系。图9的仿真条件为:障碍物半径为60 m,初始弹障距离大于500 m,且必须保持匀速直线运动,目标速度为飞行器速度的35%。通过改变飞行器横向过载,大量仿真发现随着飞行器横向过载增大,能避开障碍物的速度范围增大,横向过载9g时最高可避开约为飞行器速度175%的运动障碍物。例如图(9)中飞行器以400 m/s且横向过载9g时避开障碍物最大速度为700 m/s;当增大障碍物尺度时需要更大的横向过载;初始弹障距离越大,即保证足够的时间提前动作避开障碍物,因此能避开障碍物的尺度更大,速度更高。
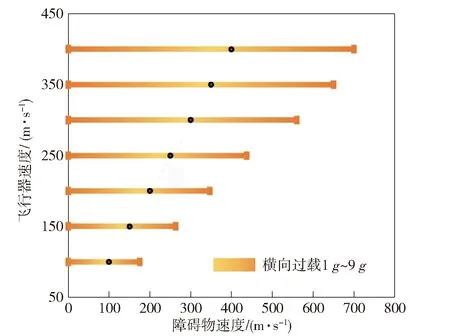
图9 飞行器速度及横向过载与障碍物速度关系
3.3 不同避障制导律对比
为了进一步探究本文避障制导律的性能,验证其特性优劣,与文献[6]和文献[20]提出的避障制导律进行仿真对比。文献[6]提出的避障制导律是比例制导项与避障项的加权之和,文献[20]提出的避障制导律针对静态障碍物设计。
图10为本文与文献[6]和文献[20]的避障制导律在运动学与动力学层面的比较,具体即弹道轨迹、弹障距离和飞行器过载的比较。图10(a)为本文及文献[6]的避障制导律对障碍物速度20 m/s 工况的仿真和文献[20]静止障碍物的弹道轨迹,图10(b) 中的弹障距离分别对应图10(a)中的弹道轨迹,发现都能够成功打击目标,同时完成对移动障碍物的躲避,但与文献[6]的避障制导律相比,本文制导律的弹道轨迹更加平滑,全局性更好;文献[20] 的避障制导律只能处理静止障碍物的情形,障碍物位于初始位置,用绿色实心三角形标记,对于运动障碍物的情况飞行器则来不及避碰。

图10 本文与文献[6]和文献[20]避障制导律对比
图10(c)为3种避障制导律的过载对比,避障过程采取的机动动作趋势基本一致但幅度不同,在绕过障碍物之后由于是比例制导律起主导作用,变化趋势更加相近。此外可看出本文所提避障制导律饱和过载持续时间短、比例小,过载曲线更加平缓,不容易出现过载的陡增,因此不会有短视的缺点。而且从方法可拓展性来看,与文献[6]避障制导律相比更易推广到高阶动力学约束,可实现整个状态空间上的广义避障;文献[20]所提避障制导律局限于处理静止及障碍物速度相对飞行器可忽略的低速情形。
最终仿真的性能比较如表2所示,从中可以看出虽然本文制导律与文献[6]避障制导律相比都能够避开障碍并击中目标,但本文制导律的全局性更好,具体体现在过载较小,弹道轨迹平缓,因此命中目标时间更短;文献[20]则不具备运动障碍物的躲避能力。
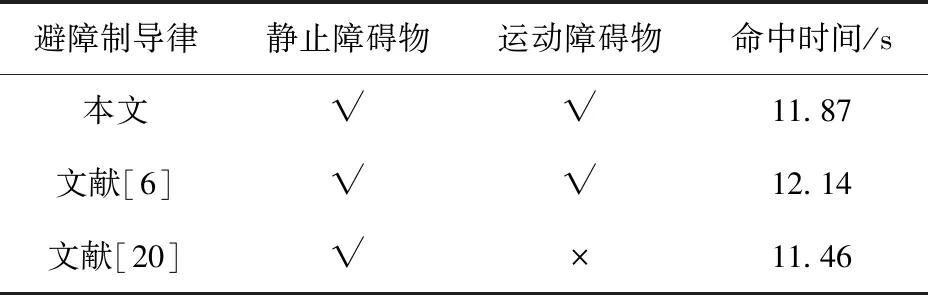
表2 不同避障制导律仿真性能对比
4 结论
本文基于CBF方法,结合速度障碍法对传统的比例制导律加以改进,构建出关于避障制导的二次优化问题,得到计算量小、实时性好的解析形式的避障制导律。随后对所提出的避障制导律进行了数值仿真验证。得到如下主要结论:
1)在小机动运动障碍物环境中,本文提出的避障制导律解决了飞行器制导中与移动障碍物发生碰撞的问题,能够同时达成躲避障碍物与打击目标的目的。
2)从全局弹道轨迹及过载特性曲线可以看出,飞行器根据障碍运动情况实时调整法向过载,因此本文提出的避障制导律具有实时性与全局性,且在无障碍物威胁时退化为比例制导律。
3)与已有避障制导律相比,本文提出的避障制导律确保飞行器能避开运动障碍物,具有更小的饱和过载占比,且弹道曲线更加平缓。
