不同流态下织构化动压滑动轴承润滑特性研究

2023-10-07吴舟赵建新毛亚洲

机床与液压 2023年17期

吴舟，赵建新，毛亚洲

(1．安阳职业技术学院机电工程系，河南安阳455000；2．河南工程学院机械工程学院，河南郑州451191)

0 前言

随着旋转机械不断向高精、高速、重载的方向发展，作为支撑旋转主轴关键零部件之一的动压滑动轴承[1]，其润滑性能直接影响整个旋转机械系统。表面织构可有效改善动压滑动轴承的润滑性能[2-4]，而流态的变化会对表面织构动压滑动轴承润滑性能造成影响，包括层流与湍流。自二十世纪六十年代以来，润滑理论得到了突破性进展，尤其是Ng-Pan理论通过引入湍流因子，建立了分析湍流流态下的摩擦副润滑特性。SHYU等[5]基于Ng-Pan理论建立的湍流雷诺方程，分析了不同润滑油黏度模型与偏心率下的湍流滑动轴承的润滑特性，得到了较高雷诺数范围下的润滑性能参数。SHENOY、 PAI[6]通过构建湍流润滑模型，研究了湍流流态对外部可调节轴承性能的影响，结果表明：负径向与负倾斜可调装置轴承具有更好的性能。SOLGHAR、 GANDJALIKHAN NASSAB[7]通过引入湍流因子分析了雷诺数、偏心率以及轴承间隙等参数对有限宽轴承润滑特性的影响，得到油膜压力的变化会对轴承润滑性能产生影响的结论。MALLYA等[8]对紊流流态下槽角为36°与18°轴承的润滑特性进行了分析，研究表明：随不对中角度的增加，轴承承载能力得到了提升。OUYANG等[9]对接触状态下水润滑轴承的动态润滑特性能进行了分析，研究表明混合润滑下，轴承的动态特性受转速与压力影响明显。汲腾龙、宋鹏云[10]开展了湍流流态下轴承结构参数与工况条件对轴承润滑性能影响的研究，结果表明连续性狭缝湍流润滑性能优于非线性狭缝。

虽然国内外学者对湍流流态下轴承润滑性能开展了一系列的研究，但却鲜有不同流态下表面织构动压滑动轴承润滑特性研究的相关报道。基于此，本文作者对不同流态状态的判据、微织构以及结构参数等对不同流态下表面织构动压滑动轴承润滑特性的影响开展系统的研究。该研究对服役于不同流态的表面织构动压滑动轴承润滑性能规律认识与工程应用具有一定的意义。

1 织构动压滑动轴承结构与流态判据

1.1 织构动压滑动轴承结构形式及基本参数

图1所示为织构动压滑动轴承模型示意与剖面示意。图中：O1为织构轴承中心；O2为旋转轴中心；e为偏心距；R为轴承半径；r为旋转轴半径；c为轴承间隙，c=R-r；L为轴承宽度；hmin与hmax分别为织构轴承的最小与最大油膜厚度。

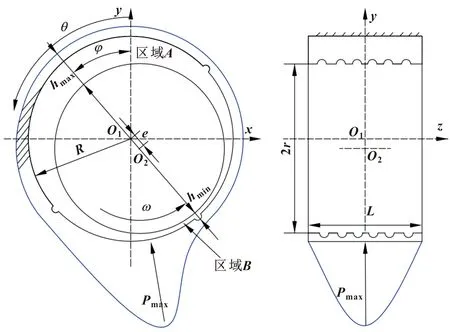
图1 织构化动压滑动轴承模型示意

在织构化动压滑动轴承润滑特性的研究中，选择的结构形式如图1所示，基本参数如表1所示。

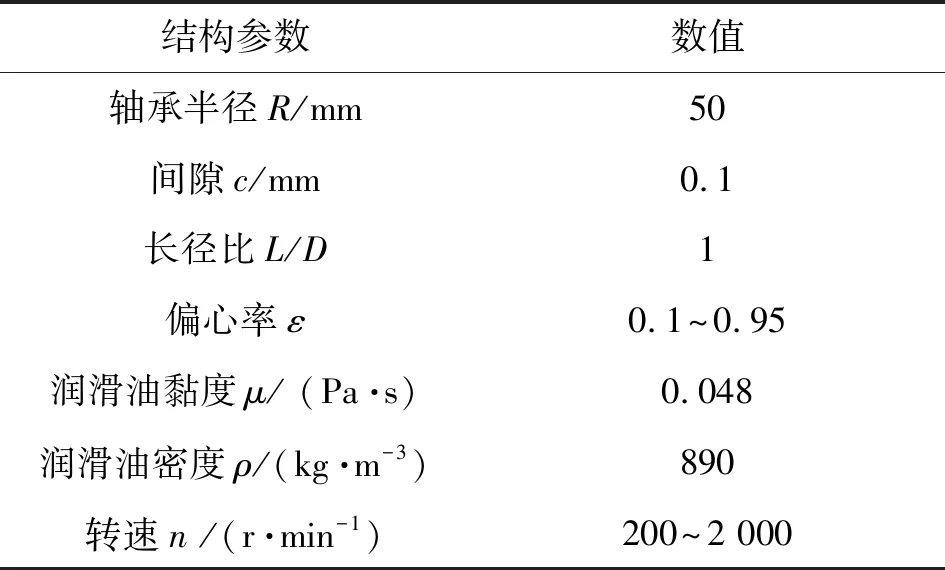
表1 织构化轴承结构参数

1.2 织构动压滑动轴承的Reynolds方程

不同润滑流态下织构化动压滑动轴承的Reynolds方程[11]为

(1)

式中：μ为黏度；h为油膜厚度；p为油膜压力；ω为轴径速度；x和y分别为xoy坐标系上x轴与y轴方向坐标；Gx和Gz表示湍流因子。

将有量纲Reynolds方程(1)进行量纲一化处理，通过引入量纲一化参数：x=Rθ，h=Hc，z=λL/2，p=μωRP/2c2，将量纲一化参数代入方程(1)后的量纲一化方程表示为

(2)

基于Ng-Pan润滑理论模型[10]，式(2)中湍流因子Gθ与Gλ分别为Gθ=1/(12+0.013 6Re0.9)与Gλ=1/(12+0.004 3Re0.98)。表面织构动压滑动轴承的油膜厚度主要是由光滑轴承油膜厚度与微坑织构油膜厚度二部分共同组成，如公式(3)所示：

(3)

动压滑动轴承油膜厚度分布如图2所示。对比图2(a)与(b)可知：圆形微坑表面织构的存在能够有效地增加油膜厚度。该油膜厚度不仅与织构的深度与半径有关，还与间距相关。间距越大，增加的油膜厚度柱间距越大；深度越深，量纲一化油膜厚度值越大。

图2 动压滑动轴承油膜厚度分布

1.3 织构动压滑动轴承的流态判据

同心圆柱转动滑动轴承，根据Taylor公式，判断其发生湍流流态的临界雷诺数Rec理论计算公式可表示为

(4)

式(4)可判断动压滑动轴承偏心率ε=0状态下的流态。通过估算可得织构轴承湍流流态下临界雷诺数的理论计算公式[12]为

Rem=(1+1.5ε2)0.5Rec

(5)

式中：ψ为间隙比，ψ=c/R；ε为偏心率，ε=e/c。

织构动压滑动轴承间隙一般在0.05～0.2 mm内变化，不同轴承偏心率湍流润滑状态下的临界雷诺数Rem如图3所示。在图3中，相同偏心率ε下，间隙比ψ越大，临界雷诺数Rem越小；随着间隙比ψ的增加，相邻间隙比ψ与之相应的临界雷诺数Rem的差值也在逐渐减小；而在相同间隙比ψ下，临界雷诺数Rem随偏心率的增加而增大。

图3 临界雷诺数随偏心率的变化

通过式(5)可判断织构化动压滑动轴承所处的流态。织构化动压滑动轴承流态(层流→紊流)转变的过程中，润滑油区域A1流态转变过程中与之相应的起始角θ1与终止角θ2可分别表示为

(6)

式中：Re=(1-aε0)Rec，ε0为转速ω0下的偏心率；a、a1与a2分别是同轴承结构形式以及工况条件相关的系数。

在织构化动压滑动轴承润滑油流态转变过程中，起始角θ1与终止角θ2随偏心率ε的变化如图4所示。其中，相同a1与a2下，起始角θ1随偏心率ε的增加而减小，终止角θ2随偏心率ε的增加而增大，且θ1和θ2180°对称；相同偏心率ε下，润滑油油膜流态转变的终止角θ2高于起始角θ1；随着a1与a2的逐渐增加，相应的起始角θ1与终止角θ2逐渐靠近对称线。

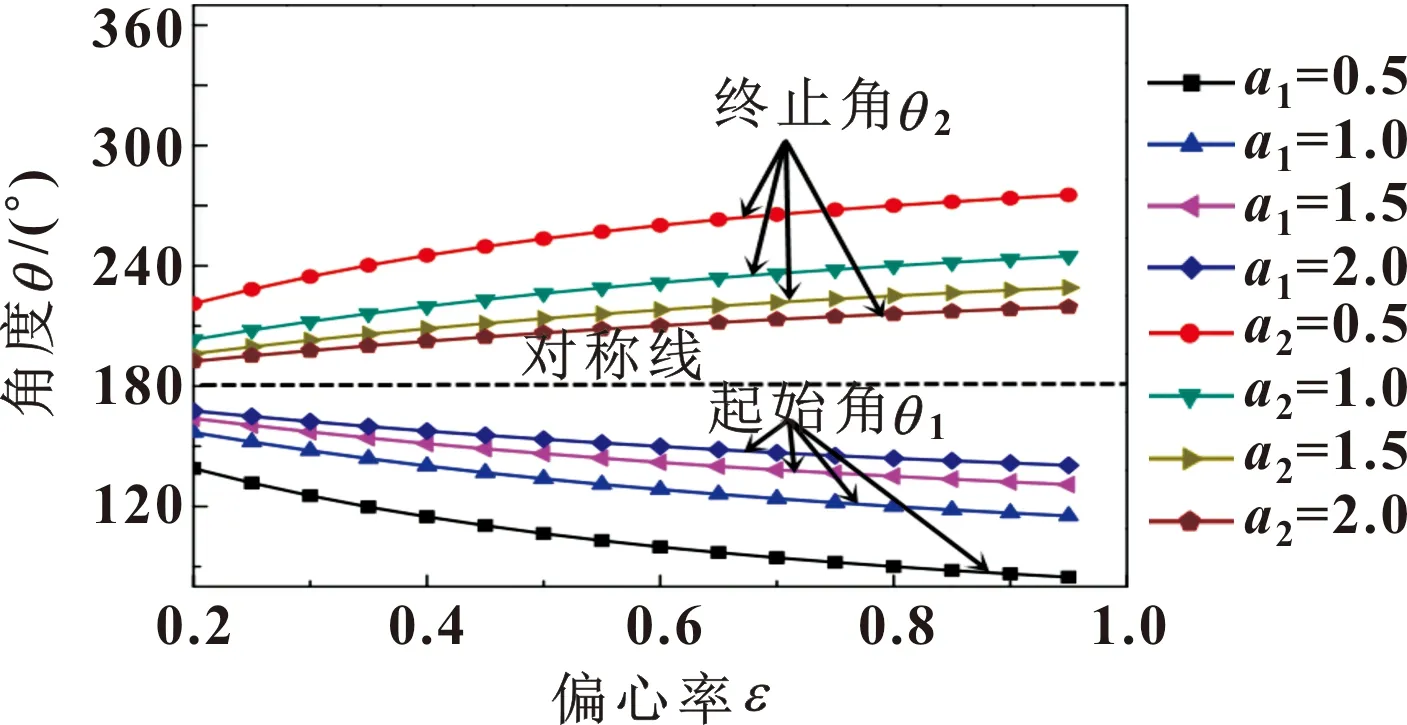
图4 起始角与终止角随偏心率的变化

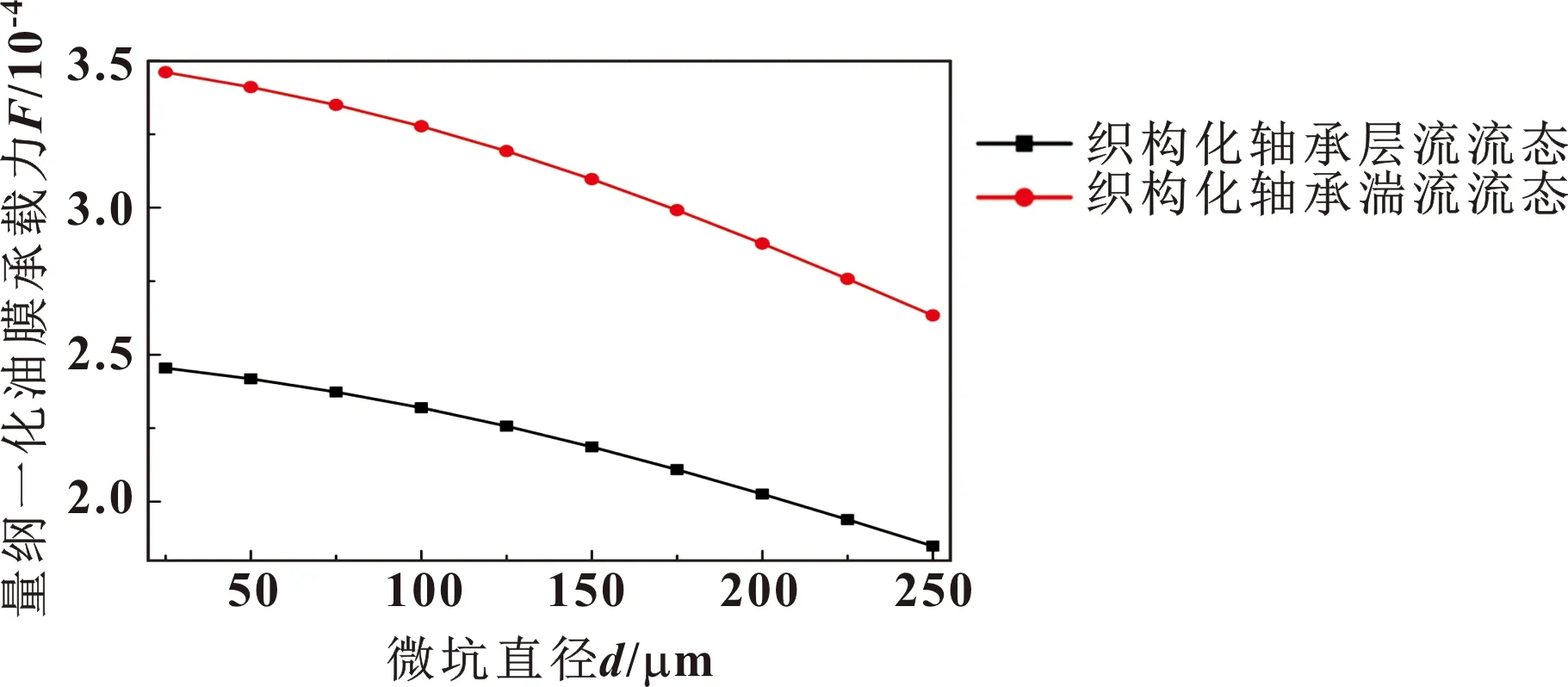
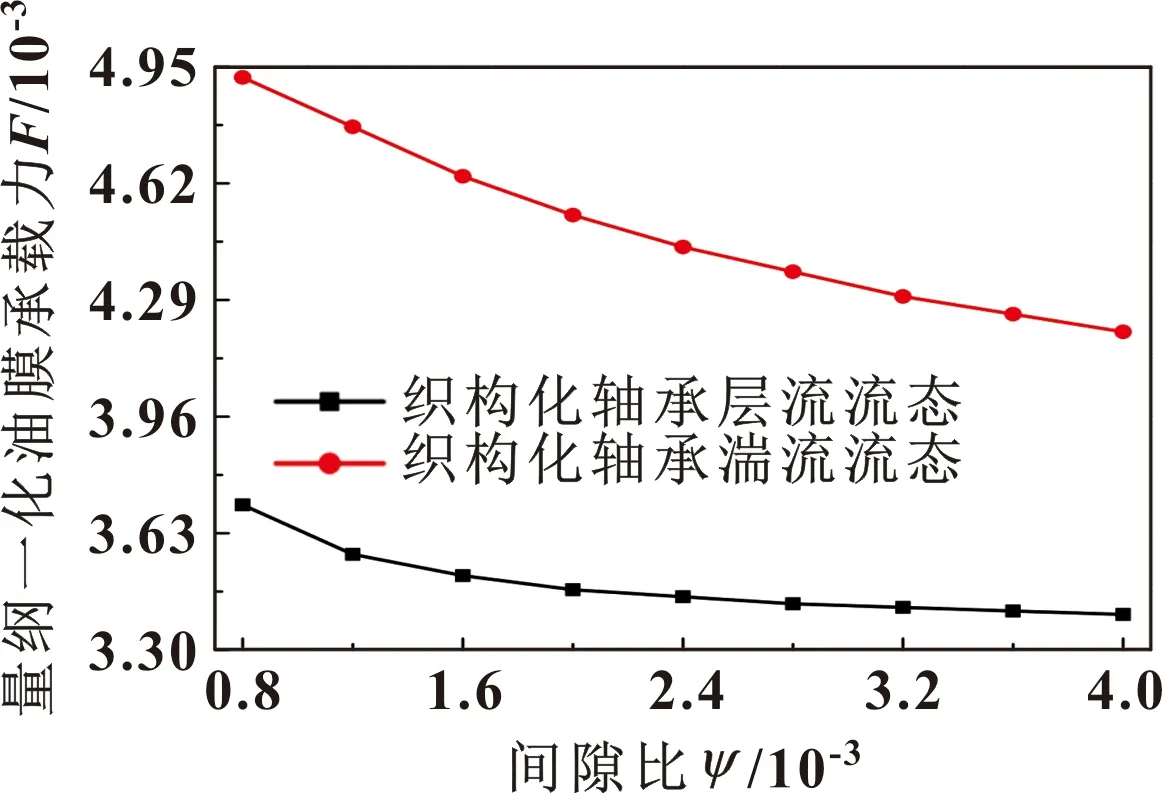
通过上述润滑油区域流态分析，当Re

2 数值计算及可靠性

2.1 边界条件与计算流程

织构动压滑动轴承采用的油膜边界包括：全Sommerfeld油膜边界、Gümbel油膜边界、Reynolds油膜边界与JFO油膜边界。由于Reynolds油膜边界可准确反映织构动压滑动轴承润滑性能的变化，计算容易且较快达到预设精度目标，故文中将Reynolds油膜边界用于织构动压滑动轴承特能分析。

文中基于有限差分法并采用超松弛迭代法对织构化动压滑动轴承雷诺方程中的油膜压力进行迭代求解。通过设置迭代结束精度的相对误差为10-5，最终确定迭代过程是否继续。详细的数值计算流程如图5所示。

图5 织构化轴承润滑特性数值计算流程

2.2 计算方法的可靠性

为了验证文中计算方法的可靠性与准确性，将文献[13-15]中的轴承结构形式与文中方法得到的计算结果进行比较。由表2可知：文中数值计算结果与文献[13-15]的结果较好吻合且误差较小，验证了采用数值方法的准确性与可靠性。

表2 最大油膜压力对比

3 结果与讨论

结合表1所示的织构化动压滑动轴承结构参数与工况条件，根据控制变量法，研究微织构结构参数、动压滑动轴承结构参数以及工况条件对织构化动压滑动轴承润滑特性的作用规律。

3.1 织构动压滑动轴承油膜压力分析

不同油膜流态下的动压滑动轴承油膜压力如图6所示。可知：不同油膜流态下的织构化动压滑动轴承油膜压力周向分布变化规律基本一致，且湍流流态下的织构化动压滑动轴承油膜压力远远高于层流流态，表明湍流油膜流态能够有效地提高织构化动压滑动轴承的膜压。

图6 不同流态下的动压滑动轴承油膜压力

湍流油膜流态下轴向与周向的织构化动压滑动轴承油膜压力变化规律如图7所示。可知：织构化动压滑动轴承油膜压力表现为两端泄口油膜压力最小，轴向中心位置X=0处的油膜压力最大，且在轴向呈现以X=0为对称轴的对称分布。

图7 湍流流态下织构化动压滑动轴承油膜压力

湍流流态下织构化动压滑动轴承在周向与轴向位置的油膜压力分布如图8所示。由图8(a)可知：由于表面织构的存在，动压滑动轴承油膜压力分布转变为锯齿状态的变化，且任意锯齿与之相应的是动压滑动轴承表面的织构点。当表面织构处于收敛区域时，动压滑动轴承系统的动压润滑作用发生了叠加，进一步增强了织构化动压滑动轴承油膜压力，所以图中的锯齿变化曲线表现不突出；当表面织构处于发散区域时，表面织构的负压效应造成收敛区域的动压作用截断，引起空化现象更明显，间隙收缩造成的动压润滑作用更加凸显，故锯齿呈现出非常显著的变化。由图8(b)可知：织构化动压滑动轴承沿着轴向位置分布的变化，相应的油膜压力分布表现为高压区与低压区交替变化的连续现象，且在轴向中心位置(X=0)处的油膜压力达到最大，轴向两端泄口(X=±0.5)处的油膜压力最小。

图8 织构化轴承油膜压力剖切图

为了进一步说明织构化动压滑动轴承油膜压力的分布变化，湍流流态下的织构化动压滑动轴承的局部油膜压力与油膜分布如图9所示。

图9 织构轴承油膜压力剖切图

由图9(a)可知：湍流流态下的织构化动压滑动轴承油膜压力的下降区域周围均存在相对的膜压上升区域，原因在于圆形微坑表面织构的分布区间会导致局部区域膜厚的增加，详见图9(b)所示。根据流体动压润滑作用机制，局部区域膜厚的增加会必然导致膜压的降低，因此图9(a)中会出现膜压降低的状况。然而，随着微坑织构内的润滑油流出，间隙发生收缩，并与动压滑动轴承系统的动压效应产生叠加，相较微坑表面织构内膜压的下降区域，微织构之外的区域出现膜压较高的上升区域，也即微坑表面织构前端出现低压区域，后端出现高压区域。

3.2 微织构对动压滑动轴承润滑性能的影响

3.2.1 微坑直径对织构动压滑动轴承承载力的影响

不同流态下织构化动压滑动轴承承载力随微坑直径的分布规律如图10所示。可知：织构化动压滑动轴承承载力随坑径的增加而逐渐减小，层流或湍流流态的织构化动压滑动轴承的承载力均在较小微坑直径下最大，也即微坑直径为25 μm时。

图10 织构动压滑动轴承承载力随微坑直径的分布

3.2.2 油膜厚度对织构动压滑动轴承承载力的影响

不同流态下织构化动压滑动轴承承载力随油膜厚度的分布规律如图11所示。可知：织构化动压滑动轴承承载力随油膜厚度的增加而逐渐下降，不同流态下的承载力与油膜厚度近似呈现负相关的线性关系。油膜厚度为1.26与1.44时的承载力分别为3.505 9×10-4和3.454 3×10-4，且有限范围内油膜厚度的承载力变化不明显。

图11 织构动压滑动轴承承载力随油膜厚度的分布

3.2.3 织构间距对织构动压滑动轴承承载力的影响

不同流态下织构化动压滑动轴承承载力与织构间距的关系如图12所示。可知：不同流态下织构化动压滑动轴承承载力随间距的增加呈现逐渐增加的变化，但该变化规律是波动性的循环变化。原因在于间距较小情况下，相邻微坑之间未发生互相干扰，随着间距的增加相邻微坑发生了相互扰动作用，引起该变化规律宏观上呈现缓慢增加，但微观上呈现小幅度的波动性变化。

图12 织构动压滑动轴承承载力随间距的分布

3.2.4 转速对织构动压滑动轴承承载力的影响

不同流态下织构化动压滑动轴承承载力与转速的关系如图13所示。可知：织构化动压滑动轴承承载力随转速的增大而呈现线性增加的变化规律。原因在于转速的升高改变了织构化动压滑动轴承的油膜压力分布进而引起其承载力的增加。较高转速下湍流流态有利于提升织构化动压滑动轴承的承载能力；而较低转速下，织构化动压滑动轴承湍流流态与层流流态下的承载力近似一致，原因在于该转速下的临界雷诺数逐渐由层流转变为湍流。

图13 织构动压滑动轴承承载力随转速的分布

3.3 结构参数对织构动压滑动轴承性能影响

3.3.1 偏心率对织构动压滑动轴承承载力的影响

不同流态下织构化动压滑动轴承承载力随偏心率的分布规律如图14所示。可知：不同流态下的织构化动压滑动轴承承载力随偏心率的增加而非线性增大，较小偏心率下的流态变化对其承载力的影响不明显，且处于湍流流态的织构化动压滑动轴承承载力始终高于层流流态。

图14 织构动压滑动轴承承载力随偏心率的分布

3.3.2 长径比对织构动压滑动轴承承载力的影响

不同流态下织构化动压滑动轴承承载力随长径比的分布规律如图15所示。可知：织构化动压滑动轴承承载力随长径比的增加而增加，但随着长径比的持续增大，其增幅逐渐变缓。长径比过大，它对其承载力的影响几乎不变，原因在于长径比的增加，虽然轴向宽度变大，承载范围增加，但是单位面积上的压力降低了，故承载力随长径比的增大增幅放缓。因此，织构动压滑动轴承的长径比选取在1～2.4内较为适宜。