基于特征融合与HPO-RVM的滚动轴承剩余寿命预测
2023-10-07栗子旋高丙朋
栗子旋,高丙朋
(新疆大学电气工程学院,新疆乌鲁木齐 830017)
0 前言
滚动轴承作为旋转机械的关键部件,决定着机械设备能否安全平稳运行。在复杂的运行工况下,随着服役时间的增加,轴承性能逐步退化,发生故障甚至导致失效。对滚动轴承的剩余使用寿命(Remaining Useful Life,RUL)进行预测,可以确定最佳维修点,实现预测性维护,减少事故的发生和经济损失,提高设备的可靠性[1]。
基于数据驱动的滚动轴承剩余寿命预测技术的研究包含2个重要方面:运行状态的特征提取和剩余寿命预测模型的建立。特征提取是关键,寿命预测是目标。良好的特征能够反映轴承的运行状态和退化趋势,而寿命预测模型则能够根据退化特征挖掘轴承的退化规律,实现准确地预测滚动轴承的剩余使用寿命。文献[2]通过双树复小波重构原始信号,得到去噪后的信号,提取相应的特征,采用BP网络对破碎机转轴进行寿命预测。文献[3]提取时域特征描述轴承的退化过程,并采用滤波器进行降噪处理,然后采用优化算法得到支持向量回归的参数,训练多个模型进行轴承寿命预测。为了能够更好地描述轴承的退化特征,提取时域、频域以及时频域特征共同构成特征矩阵。然而多维特征容易导致维数灾难。为了兼顾全面反映轴承的运行状态和计算效率,对特征矩阵进行降维处理。JENSSEN[4]提出了核熵成分分析(Kernel Entropy Component Analysis,KECA),该算法将原始非线性数据经过核函数映射到高维特征空间中,在最大保留原始信息的情况下进行降维融合。
寿命预测阶段,有学者从轴承初期开始进行寿命预测[5-6],但是轴承初始运行阶段状态平稳,对它进行寿命预测没有实际工程意义,并且非退化数据的引入将造成寿命预测的精度下降。文献[7]采用退化阶段前期的数据训练模型,然后预测轴承的剩余使用寿命。文献[8]采用时变卡尔曼滤波进行寿命预测,构造基于线性和二次函数的卡尔曼滤波模型,自动适应切换滤波模型,以处理轴承的正常运行阶段和加速退化阶段的监测数据,从而达到有效预测剩余寿命的目的。
相关向量机(Relevance Vector Machine,RVM)是在贝叶斯框架下发展起来的支持向量机的另一种改进形式[9]。该模型结合了贝叶斯原理、自动相关决策机制和最大似然等理论[10],能够处理高维,非线性、小样本等问题;具有良好的稀疏性、泛化能力和较高的预测精度,RVM的核函数不受限于Mercer条件,在核函数的选择和构建中更为灵活[11]。核函数在很大程度上决定着RVM模型的预测性能[12],因此采用猎食者-猎物优化(Hunter-Prey Optimization,HPO)算法去寻优得到RVM的核参数,该方法主要思想结合了猎食者向着猎物的方向调整自己的位置,而猎物则是向着安全的地方调整自己的位置[13]。
综上,本文作者提出一种基于特征融合和HPO优化RVM的滚动轴承剩余寿命预测方法。提取多域特征,利用特征筛选和核熵成分分析相结合,提取轴承的退化状态信息。利用HPO优化算法自适应地确定相关向量机(Relevance Vector Machine,RVM)的最佳核宽度,通过训练轴承得到寿命预测模型,将测试轴承的退化特征输入到模型中,实现轴承的寿命预测。
1 特征提取和融合
1.1 多域特征提取
1.1.1 时域特征
时域特征包括有量纲和量纲一化2种,特征值的大小可以反映设备的运行状态,提取均值、方差、均方根、标准差、最大值、最小值、峰峰值、波形指标、峭度指标等16个时域特征,记为F1-F16。
1.1.2 频域特征
对原始振动信号进行快速傅里叶变换,然后计算相关的频域特征,包括频率均值、频率标准差、频率重心等能够反映频域振动能量大小、频谱分散或集中程度以及频带位置变化的13个频域特征。记为F17-F29。
1.1.3 时频域特征
小波包分解是一种时频域分析方法,可以实现信号的高频部分和低频部分同时分解,采用这种分解方式既不会造成信息冗余,也不会造成信息疏漏。计算3层小波包分解的能量熵、奇异谱熵和8个频带的能量,共10个特征。记为F30-F39。
1.2 特征筛选
良好的退化特征应具有较强的鲁棒性和时间相关性。提取的多个特征并不全都能满足这2个特性,因此利用鲁棒性和相关性评价指标对特征进行筛选。
鲁棒性:反映特征对噪声或异常值的抗干扰能力,表达式为
(1)
式中:K为样本个数;XT(tk)是经过平滑处理后的趋势项;XR(tk)是波动项;X(tk)=XT(tk)+XR(tk)。
相关性:表示特征与时间序列的相关度,采用Spearman相关系数,计算公式为
(2)
di=rankXi-rankTi(i=1,…,K)
(3)
式中:X、T分别表示2个时间序列;di代表2个序列变量在排序后的秩差。
由于单个指标只能够评价特征在某个方面的特性,因此使用自适应加权方法构建综合评价指标:
J=ω1Rob(X)+ω2Cor(X,T)
(4)
式中:ωi为评价指标的权重。
采用Critic方法自适应确定权重。该方法综合考虑了指标间的差异性和相关性,如式(5)所示:
(5)
式中:σj为指标j的方差;ζij为相关系数。然后计算权重,如式(6)所示:
(6)
式中:ωj表示指标j的权重。
1.3 核熵成分分析
KECA是基于Renyi二次熵和Parzen窗函数提出来的。Renyi二次熵数学形式如式(7)所示:
(7)
式中:p(x)为样本集D={x1,x2,…,xN}的概率密度函数。将式(7)中的积分部分定义为
(8)
式(8)可以改写为以下等式:
(9)
(10)
式中:K为N×N的核矩阵;I是N×1的向量。对K进行特征分解:
K=EDET
(11)
式中:D=diag(λ1,λ2,…,λN);E是特征向量矩阵,E={e1,e2,…,eN}。将式(11)代入式(9)可以得到:
(12)
式中:λi和ei是按照二次熵的估值降序排列得到的。选择满足要求的前k个特征值与特征向量进行投影变换可以得到Φeca:
(13)

2 HPO算法优化相关向量机
2.1 相关向量机
tn=y(xn;w)+εn
(14)
式中:t=(t1,…,tN);w=(w0,…,wN);y(xn;w)为非线性函数;εn为高斯噪声。假设tn服从高斯分布:
p(t|x)=N(t|y(x),σ2)
(15)
由贝叶斯定理,数据集的似然估计可以写成:
(16)
式中:Φ是核矩阵;Φnm=K(xn,xm-1),Φn1=1。
根据贝叶斯规则获得权重的后验概率:
p(w|t,α,σ2)=(2π)-(N+1)/2|Σ|-1/2·
(17)
Σ=(ΦTBΦ+A)-1
(18)
μ=ΣTBt
(19)
式中:A=diag(α0,α1,…,αN);B=σ-2IN;Σ为后验方差;μ为均值。
对权重积分,获得超参数边缘概率分布:
p(t|α,σ2)=(2π)-N/2|B-1+ΦA-1ΦT|-1/2·
(20)
通过迭代计算得到超参数α和σ2的最优解:
(21)
(22)
式中:Σii表示协方差矩阵Σ中第i个对角元素。
相关向量机的核函数主要分为局部核函数和全局核函数两类:局部核函数学习能力强,泛化能力弱;全局核函数泛化能力强,学习能力弱。采取加权组合核函数,选取一个全局核函数多项式核函数和局部核函数高斯核函数进行加权组合,来提高模型的预测精度和鲁棒性,形式如下:
(23)
2.2 HPO算法原理
猎食者-猎物优化算法是于2022年提出的一种新的优化算法,具有收敛速度快、寻优能力强的特点,并且人工设置参数少。
随机生成种群的初始位置。
xi=rand(1,d)·(ub-lb)+lb
(24)
式中:d为目标个数;ub、lb分别为搜索空间的上边界和下边界。
猎食者根据下式进行搜索:
xi,j(t+1)=xi,j(t)+0.5{[2CZPpos(j)-xi,j(t)]+
[2(1-C)Zμ(j)-xi,j(t)]}
(25)
其中:x(t)为当前猎食者的位置;x(t+1)为猎食者下一个位置;Ppos为猎物的位置;μ为所有位置的平均值;Z是由下式计算的自适应参数。
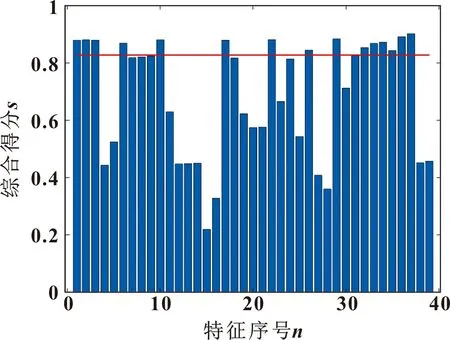
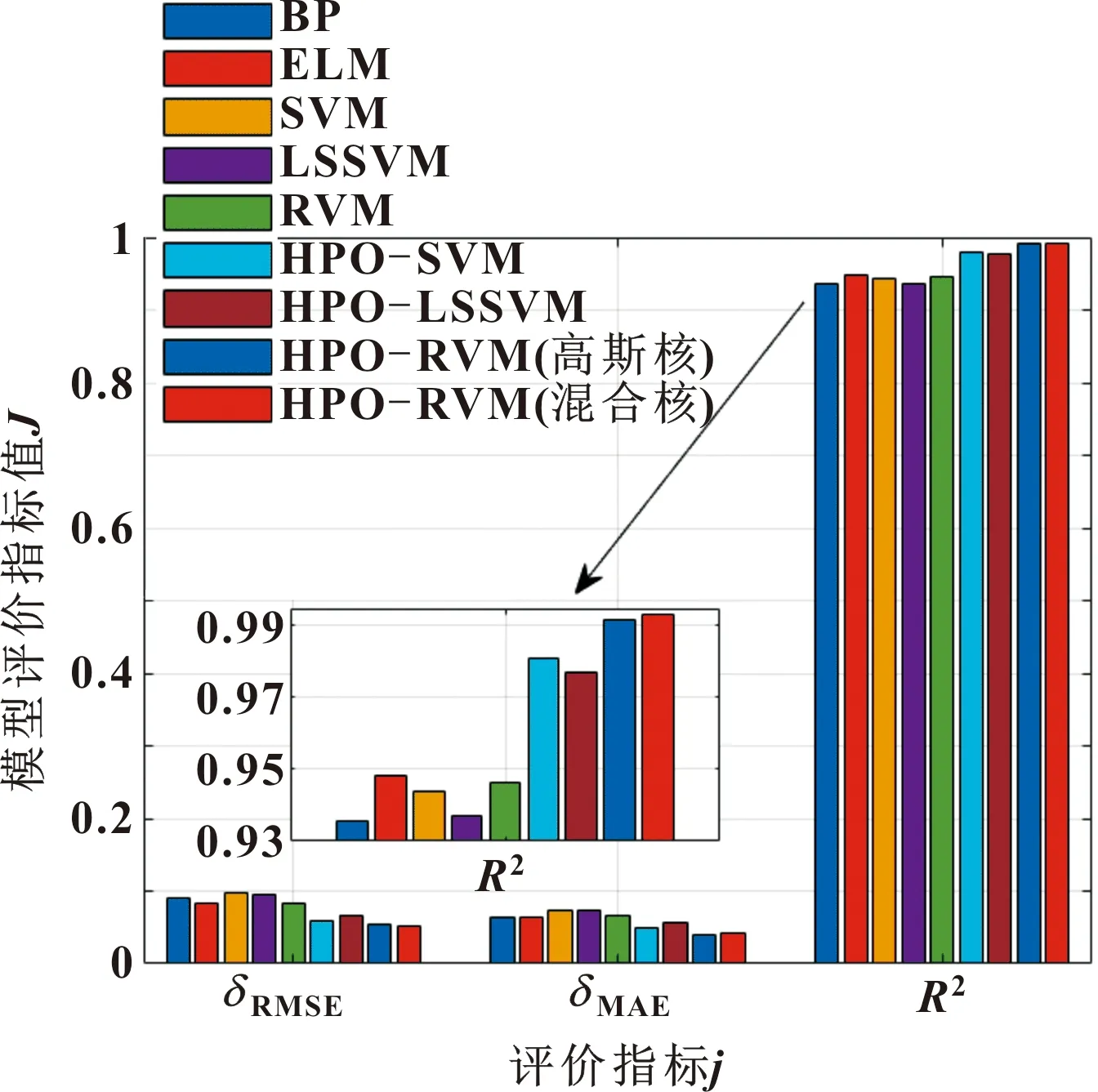
P=R1 Z=R2⊗δIDX+R3⊗(~δIDX) (26) 其中:R1和R3是[0,1]内的随机向量;δIDX是满足条件P=0向量R1的索引值;C是探索和开发之间的平衡参数,计算如下: (27) 其中:εit是当前迭代值;εitmax是最大迭代次数。 计算所有位置的平均值: (28) 计算欧几里得距离: (29) 距离位置平均值最大的搜索代理视为猎物Ppos: Ppos=xi|iis index of Max(end)sort(Deuc) (30) 为了解决则算法延迟收敛性的问题,考虑一种递减机制,如下式所示: kbest=round(C×N) (31) 其中:N是搜索代理的数量。因此,猎物的位置计算公式可写为 Ppos=xi|iis soredDeuc(kbest) (32) 为了选择猎人和猎物,结合式(25)和式(30)提出式(33): xi(t+1)= (33) 其中:R5是[0,1]内的随机数;β是调节参数。 采用HPO算法对混合核参数进行寻优。优化的具体流程如图1所示,优化步骤如下: 图1 参数优化流程 步骤1,设置种群数、迭代次数以及优化参数的上下界、目标函数。 步骤2,计算适应度值,记录最优位置。 步骤3,利用式(26)和(27)更新参数Z和C。 步骤4,根据式(33)更新猎食者或猎物的位置,并计算适应度值和最优位置。 步骤5,判断是否满足停止条件,如果满足,则输出最优解,跳转至步骤6,否则重复步骤3-4。 步骤6,利用最优解构建RVM预测模型。 剩余使用寿命定义为 RUL=Tend-Ti (34) (35) 式中:Tend为轴承失效时刻;Ti为当前监测点。为减少不同轴承间的差异,采用式(35)将轴承的剩余寿命进行归一化处理。 基于特征融合与HPO-RVM的轴承剩余寿命预测步骤如下: 步骤1,提取时域、频域、时频域特征。 步骤2,计算每个特征的鲁棒性和相关性,采用Critic方法确定评价指标的权值,然后计算每个特征的综合得分。 步骤3,选取得分最高的前15个特征采用KECA降维融合,并以贡献率大于90%的主成分作为退化特征。 步骤4,采用3σ方法确定轴承的初始故障时刻,当故障发生以后启动剩余寿命预测机制。 步骤5,根据训练数据,采用HPO寻优得到RVM核参数,代入RVM中得到HPO-RVM寿命预测模型。 步骤6,将测试集代入训练好的模型中进行剩余寿命预测,如图2所示。 图2 寿命预测流程 步骤7,模型性能评价。 评价指标:均方根误差δRMSE、平均绝对误差δMAE、决定系数R2。前2个评价指标越小说明模型的预测能力越好,第3个评价指标越大说明模型的预测能力越好[14]。 (36) (37) (38) 文中实验验证采用的是XJTU-SY全寿命滚动轴承数据集,图3所示为搭建的实验平台。测试所采用滚动轴承的型号为LDK UER204。实验共测试了3种工况共计15个轴承,具体工况信息如表1所示。传感器为PCB 352C33加速度传感器,采样频率25.6 kHz,每间隔1 min,采样1.28 s。详细实验过程和信息参考文献[15]。 以工况1中的5个轴承为研究对象进行滚动轴承的剩余寿命预测研究,分别命名为轴承1-1、轴承1-2、轴承1-3、轴承1-4、轴承1-5。 以工况1为例,提取时域、频域、时频域39个特征,然后归一化。轴承1-1的特征如图4—6所示。然后根据评价指标鲁棒性和相关性计算每个特征的得分,采用Critic方法确定2个评价指标的权重,然后得到综合评价指标。 图4 轴承1-1时域特征 图5 轴承1-1频域特征 图6 轴承1-1时频域特征 根据式(4)计算工况1下5个轴承各个特征综合得分的平均值。如图7所示,选出前15个得分最高的特征,依次为37、36、29、22、2、10、1、3、17、34、6、33、32、26、35。可以看出:筛选出的特征包括时域特征、频域特征和时频域特征。 图7 工况1轴承特征筛选 利用KECA方法将筛选出来的特征指标进行降维融合,从图8中可以看出:工况1的各个轴承第一主成分的贡献率都大于90%,因此选取第一主成分作为轴承的健康指标。为降低不同轴承间的差异性,对健康指标进行归一化处理。为了降低噪声或异常值引起的指标波动,采用局部加权回归方法进行平滑处理,得到工况1的健康指标如图9所示。 图8 工况1各轴承主成分贡献率 图9 工况1轴承健康指标 轴承运行初期,退化特征不明显,特征指标平稳,对它进行寿命预测工程意义不大。当发生早期故障以后,轴承开始退化,启动剩余寿命预测。在进行寿命预测时只是用退化阶段的数据,避免了非退化数据对寿命预测的精度造成干扰。文中采用3σ方法检测轴承的早期故障时刻,从而确定寿命预测的初始时间,具体方法参考文献[16]。得到轴承1-1到轴承1-5发生故障的时刻为70、36、59、121、34 min。因此将发生早期故障以后的退化指标归一化作为剩余寿命预测的数据,从而提高预测的精度。 寿命预测阶段,以前4个轴承作为训练集训练寿命预测模型,最后1个轴承作为测试集,验证模型的预测性能。采用HPO算法寻优得到RVM的组合核参数,HPO算法的种群数设置为100,最大迭代次数为100,得到的最优参数用于RVM预测模型的训练。将待测数据输入到模型中进行预测,得到的寿命预测结果如图10所示。可以看出:预测的总体趋势与实际寿命百分比接近,大部分实际值都在预测结果95%的置信区间内。 图10 所提出的预测模型预测结果 将文中提出的预测模型与BP神经网络、极限学习机ELM、支持向量机SVM、最小二乘支持向量机LSSVM、相关向量机RVM、优化支持向量机、优化最小二乘支持向量机、优化高斯核函数的相关向量机等预测模型进行对比。预测结果如图11所示。 由图11可以看出:文中所提的模型预测结果更加接近真实值,文中模型具有一定的优势。然后计算各个模型预测性能评价指标。δRMSE和δMAE值越小越好,R2越大越好。由图12可以看出:文中所提的模型δRMSE和R2均为最优结果,δMAE指标仅次于基于高斯核函数的相关向量机模型,但结果相近,总体上文中所提的模型更具优势。 图12 不同预测模型预测结果评价 将文中采用的HPO优化算法与常用的经典优化算法粒子群优化算法(PSO)、遗传优化算法(GA),以及较新的优化算法哈里斯鹰优化算法(HHO)、晶体结构优化算法(CRYSTAL)等进行对比试验,得到预测结果的评价指标如图13所示。可以看出:HPO优化算法可以取得较好的预测结果。 图13 不同算法优化模型预测结果评价 文中是以最小均方根误差作为HPO优化RVM核参数的目标函数,实际应用中可以根据需要设置不同的目标函数,如δRMSE、δMAE、1-R2、δRMSE+δMAE+(1-R2)等最小值作为目标函数。当采用以上目标函数训练模型,测试模型的预测性能如图14所示。可以看出:在训练模型时采用不同的目标函数可以使相应的指标达到最小值,以满足相应的需求。 图14 不同目标函数优化模型预测结果评价 文中提出基于特征融合与HPO-RVM的滚动轴承剩余寿命预测方法,利用轴承全寿命数据集进行方法验证,得出以下结论: (1)采用综合评价指标筛选出来的特征包含时域、频域、时频域特征,将筛选出来的特征进一步用KECA降维融合,选取能够反映90%以上特征信息的主成分作为退化特征,不仅降低了计算量,而且特征信息更加丰富,避免了单一特征不能较好地反映轴承的退化特征。 (2)采用检测到轴承发生故障以后再进行寿命预测的策略,避免了非退化特征对剩余寿命预测精度的影响。 (3)HPO优化混合核RVM的预测模型,其预测精度优于BP、ELM、SVM等模型;所采用的优化算法在此实验中优于PSO、GA等算法;并讨论了不同的目标函数对预测模型的影响。综合说明文中所提的寿命预测模型具有一定的优势。2.3 RVM参数优化
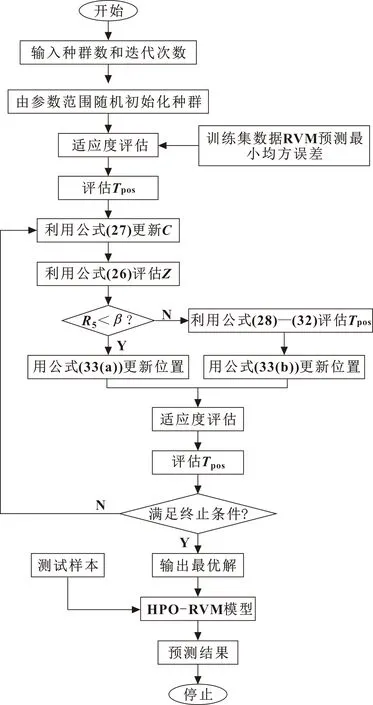
3 寿命预测流程


4 实验仿真验证
4.1 数据集介绍
4.2 退化特征的构建





4.3 滚动轴承寿命预测



5 结论
