基于电机拖拽系统的垂直管柱振动响应特性试验研究

2023-10-07宋微张亚楠王素玲董康兴岳欠杯

机床与液压 2023年17期

宋微，张亚楠，王素玲，董康兴，岳欠杯

(东北石油大学机械科学与工程学院，黑龙江大庆 163318)

0 前言

管柱作为钻采开发的重要设备，承担着油气采集、运输、注水、注气等任务，在世界海洋油田范围内广泛应用[1]。细长的管柱受水流冲击，不仅要承受外载荷作用在上面周期变化的作用力，还会在流体作用下发生涡激振动，由此产生的共振现象是造成管柱疲劳破坏的主要原因。同时管内流体的流动也会使管柱自振频率发生改变，使管柱共振概率变大，因此考虑内、外流同时作用的管柱振动，已经成为海洋石油钻采运输领域的关键工程问题之一[2-3]。

众多学者对细长柔性管柱进行了试验研究，分别得到了水下管柱的动力响应和流体特征。MOE、WU[4]开展了刚性圆柱振动试验，通过改变管柱质量比，对静水中的管柱自振频率进行了测试，结果发现质量比较低的圆柱响应频率与静水中的自振频率区别很大，使得自激振动与受迫振动结果不同。HUERA-HUARTE、JIMÉNEZ-GONZLEZ[5]对串联排列的管柱进行了干涉试验研究，分析了间距比对锁振的影响。KANG、 JIA[6]对大跨度柔性管柱开展了大量的涡激振动试验，给出了涡激振动试验研究方法，并对涡激振动现象进行了较为全面的总结。周守为等[7]对海洋隔水管涡激振动进行了试验研究，发现锁振现象发生在一定的频率范围内，并对管柱模态进行了分析，研究了立管模型在不同模态下的振动趋势和应变大小。崔阳阳等[8]对不同参数的管柱进行了试验研究，得到了其动力响应变化规律。唐国强等[9-10]对海洋柔性立管进行了涡激振动响应试验，得到了均匀流下管柱多模态之间振幅响应。

目前大多数的试验研究没有考虑内流的影响，而管柱一般用于石油、天然气及多相混合的气液输送。内流与管柱之间的耦合作用使管柱振动响应发生变化，因此，本文作者通过构建内、外流下垂直管柱振动响应测试试验平台，研究水下垂直管柱在不同参数下的振动响应规律，通过物理模型试验提高对含内流的水下垂直管柱振动响应特性和机制的认识，为水下采油作业管柱布置和振动抑制方法提供依据。

1 相似比模型换算

由于深水管柱原型试验测试困难，因此可以采用相似比模型进行试验研究。相似比的换算要保证试验中的模型能真实反映实际工况，能够反映所处环境下的涡激振动情况，通过对试验结果进行统计分析得到其振动响应规律。采用相似理论[11]，按照重力相似准则进行有比尺换算，得到速度比尺和长度比尺分别为

(1)

(2)

文中选取南海某海域实际作业钻井管柱为研究对象，将实际工况参数换算为试验参数，主要参数见表1—3。

表1 海洋管柱参数与试验参数

表2 实际工况海流速度与试验工况外流速度单位：m·s-1

表3 内流速度对比单位：m·s-1

2 试验平台搭建及方案设计

试验在东北石油大学海洋油气储藏试验水槽上开展，水槽长5 m、宽3 m、深3 m。搭建单层垂直管柱内、外流测试试验平台如图1所示。

图1 水槽试验台

该试验平台主要包括管柱支架、试验管柱、滑道、电机、加水泵、流量计、数据测定与采集装置等，部分试验装置见图2。电机拖曳支架产生相对外流速度，形成外流循环系统；通过加水泵对垂直管柱施加内流形成内流循环系统，并通过流量计控制内流速度。支架上方尼龙夹通过线切割预留多孔，方便双管安装测试。

图2 试验装置

对多种工况下垂直管柱的自振频率、管柱振动响应进行测定，获得试验数据，据此分析内、外流速，间距比等因素对管柱振动响应特性的影响。试验内容包括：

(1)单管柱涡激振动试验测试研究。通过相似比试验探讨不同内、外流速下单管柱振动响应规律。

(2)双管柱涡激振动试验测试研究。固定内流速度，通过改变外流速度和串联双管柱间距比探讨串联双管振动响应规律。

3 试验结果及分析

3.1 自振频率分析

通过敲击试验测定管柱自振频率，首先测定管柱内无水且水槽中也无水的工况，然后测定管柱和水槽分别充水，最后测定管柱和水槽都充水的工况。锤击法敲击垂直管柱中部位置，通过功率谱分析其应变衰减信号得到管柱对应自振频率如表4所示。

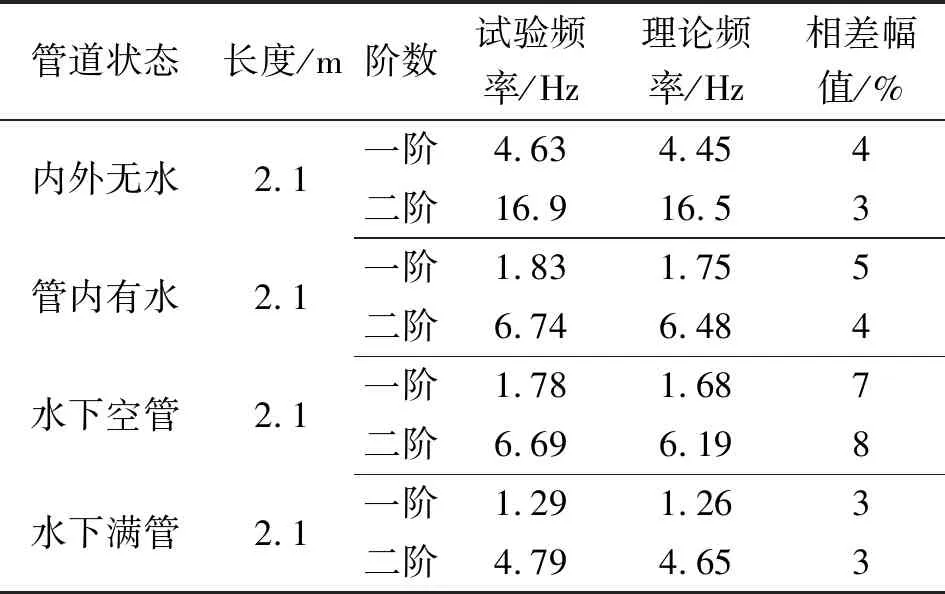
表4 不同工况下管柱自振频率

由表4可知，试验结果与通过文献[12]中理论公式计算的结果吻合较好，管柱内、外都为空气时自振频率最高，随着管内、外充水，自振频率降低，水下满管时对应一、二阶自振频率最低，这与理论公式计算得到的自振频率规律一致。试验结果较理论结果数值偏大，这是由于理论计算时将附加质量系数取为1，而试验过程中由于介质的存在使得管柱附加质量不同，并且质量比越大自振频率越小，在以往的试验中大多忽略了介质因素，而直接测得管柱的干模态，测得的自振频率较大，与实际工况并不相符。

改变管柱内流速度，再次测定外部有水时管柱自振频率，结果如表5所示。

表5 不同内流速度时管柱自振频率

由表5可知：随着内流速度的增加，管柱一、二阶自振频率均减小，使管柱的振动响应向低阶频率靠近。由此可知，管柱在较小的外流速度下容易发生共振现象，因此管柱的振动响应不能忽视内流的影响。

3.2 不同外流速度下垂直管柱振动响应分析

将安装好的垂直管柱放入水槽中后，按照试验设计分别设定相对水流速度u=0.22、0.31、0.36、0.45 m/s，固定内流速度v=0 m/s，分析不同外流速度时垂直管柱的振动响应特性，将测试得到的应变值通过模态分解法转换成垂直管柱对应点的位移值，并进行无因次处理，图3所示为管柱3/4、1/2、1/3、1/4(分别对应点1、2、3、4)4个位置在4种流速下的位移响应时程变化曲线。可以看出：4个位置位移幅值不相等，这是由于垂直管柱长细比较大，各点处位移响应并不相同，这与刚性垂管振动响应存在明显区别。

图3 不同外流速度时各点位移时程曲线

从图3中还可以看出：各测试点都随着外流速的增大位移响应单调增大，均在u=0.45 m/s时出现位移最大值。4个测试点在外流速度u=0.22、0.31、0.36 m/s时，点2位移幅值最大；外流速度u=0.45 m/s时，点3位移幅值最大，点2位移幅值最小。

为了进一步探寻外流速度对管柱振动响应的影响，给定内流速度v=0 m/s，外流速度u=0～0.6 m/s，外流速度每级增加0.01～0.05 m/s。图4所示为管柱测试点2在该流速区间内的位移最大值。

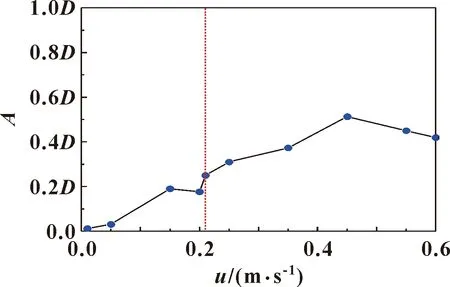
图4 不同外流速下点2位移最大值

可以看出：流速分为[0.01，0.2]m/s和(0.2，0.6]m/s 2个区间，管柱位移在u=0.15 m/s时达到最大值，此时发生了一阶共振；u=0.21 m/s时位移增大，说明此时已经跳出锁振区域，在(0.2，0.6]m/s内又出现了这种情况，u=0.45 m/s出现峰值，随后振幅随流速的增大而减小，与涡激振动理论中对共振范围的判断一致。由此也可以判断，外流速度u=0.22、0.31、0.36 m/s时，主要以一阶振动占主导，此时点2位于一阶模态峰值处，因此其位移响应最大，而u=0.45 m/s时，以二阶振动占主导，此时点2处于二阶模态拐点处，此时位移响应最小，随着流速的增大参与振动的模态阶数增多，并且高阶模态逐渐占主导。

3.3 不同内流速度下垂直管柱振动响应分析

为了考察内流速度对管柱振动响应的影响，分别测定外流速度为u=0.22、0.45 m/s，内流速度分别为v=0、0.15、0.25、0.35 m/s时，管柱的振动情况，将测得的应变通过模态分解法得到垂管各点位移，其最大值比较如图5所示。

图5 不同内、外流速下管柱位移最大值对比

由图5可以看出：同一外流速度下，管柱4个测试点的位移振幅最大值都随着内流速度的增大而增大，这是由于内流介质在管道内产生加速度，其对管道产生作用力，从而引起附加振动使振幅增大。4个测试点都呈现出外流速度越小、位移振幅随着内流速度的增大越明显的趋势，说明内流速度在外流速度相对较低时对管柱的振动影响越明显。

3.4 不同外流速度下串联双管柱振动影响分析

串联排列的双管柱是采油工程中常用的多管柱系统构型，它是更复杂的多管柱布置方式的基础。因此文中通过变换不同间距比和流速，分析其振动响应规律。

设定外流速度分别为u=0.22、0.31、0.36、0.45 m/s，内流速度v=1.5 m/s，间距比分别为L/D=2、3、4、5，前、后管柱2点处位移时程变化曲线如图6所示。可以看出：间距比L/D=2时，前、后管柱位移都随着流速的增大而增大，前管柱4种流速下的位移分别为0.17D、0.27D、0.31D、0.39D，后管柱位移分别为0.19D、0.29D、0.36D、0.45D，始终小于单管柱在各流速下的位移0.26D、0.33D、0.37D、0.51D；间距比L/D=3时，4种流速下的前管柱位移分别为0.18D、0.23D、0.32D、0.37D，后管柱位移分别为0.22D、0.32D、0.35D、0.49D，较上一间距比的幅值变化不大；间距比L/D=4时，前管柱振幅仍小于单管柱，分别为0.258D、0.31D、0.32D、0.51D，后管柱振幅分别为0.36D、0.43D、0.46D、0.65D，后管柱的振动幅值大于单管柱；间距比L/D=5时，前管柱位移分别为0.259D、0.3D、0.33D、0.52D，后管柱位移分别为0.358D、0.42D、0.45D、0.64D，与间距比L/D=4时差别不大。

(a)L/D=2；(b)L/D=3；(c)L/D=4；(d)L/D=5

对比不同间距比前、后管柱与单管柱在不同流速下的位移最大值，如图7所示。可以看出：各间距比下前、后管柱的振动响应幅值都随着外流速的增大而增大，并且后管柱振动幅值始终大于前管柱。L/D=2、3时各流速下前、后管柱的位移均小于单管柱，L/D=4、5时前管柱位移增大到与单管柱相近，后管柱位移幅值大于单管柱位移幅值。