初中数学教学中学生建模能力的培养策略

张宝瑛

【摘要】新课程背景下，各科教师在实践教学的过程中，要不断加大对学生创新精神、应用能力的培养力度，促使学生直观认识学习与社会、生活的联系.数学教育是义务教育的关键构成部分，数学建模则是帮助学生将数学与社会、生活建立联系的桥梁.因此，在初中数学课堂上培养学生的建模能力是数学教学改革的重点研究课题之一.文章主要围绕初中数学教学中学生建模能力培养的有效策略展开深入研究.

【关键词】初中数学；建模能力；培养；策略

新课程背景下，对学生综合素质的培养成为广大教育工作者重点关注的话题.对数学科目而言，其学科核心素养由几部分组成，数学建模素养则是其中之一.在初中数学教学课堂上，对学生建模能力的培养，既是重点，也是难点.新课标也有明确指示要让学生灵活应用数学模型处理数学问题，重视将知识与应用相结合，以此促进学生应用能力、创造能力的提高.基于此，在初中数学课堂上，教师要注重为学生营造良好的学习环境，引导学生深入理解数学知识，培养数学建模能力，达成新课改培养要求.

一、数学建模概述

《义务教育数学课程标准（2022年版）》中明确提出核心素养囊括了模型思想及应用意识.数学学科的模型意识更加关注学生在实际生活中抽象出数学问题，运用数学模型对不等式、方程、函数等相关问题实施解决，以促使学生充分体会数学知识的实用价值.就应用意识而言，其更注重学生主动利用概念、原理、方法等解释实际生活中的问题.另外，数学建模过程还是综合各数学素养解决实际问题的过程.例如，将数学情境抽象成数学符号进行推导，运用几何直观在实际问题中抽象出几何模型，利用几何知识解决实际问题，或者是通过数据分析的理念应用构建相应的统计模型.鉴于此，数学建模不仅有助于学生运用相关数学知识解决实际问题，还能促使学生灵活地运用有关数学知识，加强各知识点之间的联系，并构建与自身学习需求相符合的知识结构，提升自身建模意识及建模能力.

二、初中数学教学中学生建模能力的培养策略

（一）迁移已有知识，构建数学模型

数学知识的学习过程也是从旧知识过渡到新知识的过程，数学模型构建也应该从学生已有的知识、经验出发，忽略影响模型的无关因素，抓住关键内容，建立与实际问题相符的数学模型，这样既有利于提高学生的探究能力，也能够培养学生的数学模型构建能力.教师要注重学生对已有知识、方法的迁移，在教学中融入丰富的资源和素材，体现数学抽象知识与具体现象之间的联系，让学生掌握数学模型的构建方法，通过数学模型将数学概念、定理和具体的问题联系起来，这样学生才能更好地运用已有的知识与经验，去探索新的知识，解决新的问题，实现对知识的融会贯通，提高自身的数学模型构建能力.例如，某个学校要在长120m、宽80m的操场上修建6条并排跑道，如何设计比较合理？教师可以通过多媒体展示操场的样子，并给学生展示有关跑道的知识，让学生了解跑道的规格.操场的跑道一般由直道和圆弧跑道连接而成，并且直道应该尽可能长，圆弧跑道与直线跑道应该相切连接.这样学生就可以迁移以往的作图知识，将实际问题转化为数学问题，通过直线与圆弧的连接设计学校的“跑道”，将几何知识迁移到实际的现象中，将学校的跑道设计转化为几何模型.知识的迁移有利于引导学生运用数学知识和方法分析相关问题，并建立实际问题与数学知识之间的联系，培养用数学思想分析问题的习惯，提高学生的模型构建能力.

（二）运用假设思想，推演数学模型

（三）依据问题启发，培养学生的建模意识

初中数学的课堂提问是数学课堂实际教学的重要部分，课堂提问是活化学生自身思维的关键.在初中数学的实际教学中，恰当的提问往往可以指導学生的思考方向，促使数学课堂的教学活动得到有效开展.因此，数学教师可灵活地通过问题启发，促进学生的建模意识提高，从而提升学生的建模能力.具体来讲，数学教师在备课的时候，需与教学内容相结合，依据学生自身的认知发展区，设计具备启发性、开放性的数学问题，从而使学生在思考数学知识的过程中，增强建模意识.除此之外，数学教师需依据数学教材的相关内容及学生的实际学习需求，设计具备创新性的问题，营造良好的学习氛围，拓展学生学习视野，以促使学生形成相应的数学思维.在实际解题过程中，数学教师在注重培养学生的建模意识的同时，还可通过问题启发指导学生分析相关数学问题，指导学生思考：“题目中的已知条件都有什么？有什么要求？该怎样解答？可将其简化为什么问题？”经过问题引领，学生在实际思考过程中就能抽象出几何模型，从而实现对数学问题的有效解答.教师以问题为出发点，能使抽象的数学问题简洁化、直观化，从而使学生自身的建模意识得到有效增强.

（四）建模思维拓展，发散学生思维

在初中数学的实际教学中，拓展建模思维通常对学生自身的建模能力提高有着重要影响，其不仅有助于激发学生学习数学知识的热情，而且能使学生主动探究未知的知识，以促进学生自身的创新思维强化，从而在使学生充分掌握相关知识的同时，促进学生的良好成长与发展.例如，在对“一次函数的应用”开展教学时，为了使学生充分掌握相关知识，并促使学生自身的建模思维得到有效发展，数学教师可依据教学内容给出例题，具体为：“移动公司设置了新业务，即全球通的月租为50元/月，每分钟通话的费用为0.4元，而快捷通不需要月租，每分钟通话的费用为0.6元，哪种业务的收费更加划算？”依据教师提出的问题，学生可先浏览数学题目，试着构建一次函数的数学模型，设每月的通话时间为x分钟，消费为y元，全球通的业务每月花费y1=50+0.4x，而快捷通的业务每月花费y2=0.6x，以此为基础，对两个方程式进行对比，当y1>y2的时候，可知50+0.4x>0.6x，此时x<250，即快捷通的业务更划算，与之相反，若x>250，则全球通的业务更加合适，而当x=250的时候，则表明两个套餐都可以.因此，教师在实际教学时，需引导学生通过模型构建处理实际问题，以促使学生清楚地了解一次函数与一元一次不等式之间的关系，从而在让学生形成建模思维的同时，强化学生的建模能力.

（五）创设生活情境，培养建模能力

（六）开展实践活动，提升建模能力

数学模型的构建主要是为了从现实问题中提取出关键的信息，通过分析、假设、推演等一系列活动，构建出能够体现现实问题与数学知识之间联系的数学模型，并运用数学模型来快速地分析和解决相关的数学问题.因此，教师要深入研究初中数学教材知识，并将知识融入丰富的实践活动中，引导学生积极参与各项实践活动，通过实践活动提升学生的建模能力.在实践活动中，学生能够发挥自身的主体性，积极运用各种方法尝试构建模型，转变以往被动学习方式，有了更多的自主空间.这样，学生的潜能才能够被充分释放，并在参与和交流的过程中，深入理解数学模型的本质，提高自身的建模能力.例如，教师可以让学生拿出一张长10cm、宽8cm的长方形白纸，并标明A，B，C，D（如下图所示），然后將其一角沿直线AE翻折，使得翻折后D点正好落在BC边上的F点.然后教师提问：“EC的长度是多少？”学生给出如下解题过程：假设EC的长度为xcm，依据折叠的性质，可以得到AF=10cm，又AB2+BF2=AF2，可以得出BF=6cm，则FC=4cm，在Rt△EFC中，EF=（8-x）cm，依据勾股定理得（8-x）2=42+x2.这样就将实际的操作转化为数学函数问题，并成功构建函数模型，通过函数有效地解决了实际问题.这一过程不仅能够提高学生的动手能力、思考能力，让学生养成良好的探究习惯，而且能深化学生对数学建模的认识，不断提升学生的建模能力.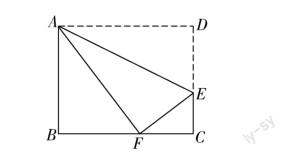

结 语

综上所述，在初中数学课堂上培养学生的建模能力，在增强学生自主学习能力、思维能力和提高解题效率等方面具有不容小觑的作用.随着年级的提升，学生需要掌握的数学内容越来越多，难度不断加大，给学生带来了不小的学习压力.而传统教学模式下教师惯用的题海战术难以从根本上解决此问题.基于此，教师需要及时转变教学观念，拓展教学内容，以问题为工具，培养学生的建模意识，还可创设生活情境，使学生的数学建模能力得到有效培养，进而促进其数学核心素养的提高.

【参考文献】

[1]朱燕.初中数学教学中学生建模能力的培养探究[J].数理化学习（教研版），2021（1）：15-16.

[2]糜玉.初中生数学建模能力的培养方略[J].数学大世界（中旬），2021（1）：35.

[3]刘香英.初中数学建模能力培养[J].教育，2020（39）：86.

[4]曹丽娟.学科核心素养下如何培养初中学生数学建模能力[J].中外交流，2020（7）：175.

[5]谭秋漪.核心素养视角下培养初中生良好数学建模能力的方法[J].考试周刊，2020（43）：73-74.

[6]徐山.培养初中生数学建模能力途径思考[J].数学大世界（下旬），2019（11）：21.