长航时旋转调制惯导系统试验测试评估

于旭东，李 鼎，高立夫，雷 雯

（1.国防科技大学 前沿交叉学科学院，湖南 长沙 410073；2.国防科技大学 南湖之光实验室，湖南 长沙 410073；3.海军装备部驻湘潭地区军事代表室，湖南 湘潭 411100）

1 引言

惯性导航系统（简称惯导系统）是利用惯性敏感器、基准方向和最初位置，来确定运载体方位、位置和速度的自主式推算导航系统和空间基准保持系统。它完全依赖载体自身设备进行导航，与外界声、光、磁、电不发生任何联系，实现了“封闭式”精确导航，因而具有隐蔽性好、不受气象条件和人为外界干扰等突出优点［1］。为了提高长航时导航精度，旋转调制技术被广泛应用于光学陀螺惯性导航领域［2-4］。旋转调制方案、误差标定与补偿，以及阻尼方案成为研究关注的重点［5-7］。随着惯性器件精度的不断提升和旋转调制方案的不断优化，惯性导航系统的精度不断提高，逐步满足舰艇长航时导航的需求。

长航时惯导系统在正式应用前，需要在不同启动条件和不同航行条件下进行多组导航测试，以评估其导航精度［8］。随着导航系统精度的不断提升，单次导航实验周期越来越长，按照国军标等传统考核方法，一般每种状态下的试验航次为8，需要在完成一个实验航次的情况下再进行下一航次导航，这导致长航时惯导系统的导航测试耗费大量的资源与时间成本［9］。

为了提高长航时惯导的导航精度，系统采用较长的对准时间，一般在4 小时以上。通常情况下，自标定、自对准路径和导航过程中旋转调制的路径一般并不一致，每个阶段的旋转调制方案单独完成各自的任务，当系统需要重新标定对准或每次标定对准完成后进入旋转调制状态时，需要更改旋转方案，以达到最优的导航效果。考虑到自标定方案和旋转调制方案的设计原则并不矛盾，本团队介绍了一种兼具自标定、自对准功能和旋转调制功能的一体式方案［10-11］，将惯导系统在自标定、自对准状态和导航过程中的旋转路径进行统一，使得惯导系统从启动开始采用同一种旋转调制路径，统一惯导系统在自标定、自对准状态和旋转调制状态间的旋转路径是缩短试验测试周期的必要前提。

本文结合前期研究成果提出了一种更高效快捷的船用旋转调制惯导系统长周期导航测试方法，开展了实验室原理验证，该方法可以大幅缩短导航系统测试及型号研制的周期，为长航时惯导装备研制、改进设计和试验鉴定提供科学依据和重要技术支撑。

2 基本原理

2.1 旋转调制惯导系统误差特性

根据φ角误差方程建立惯导系统误差传播模型：

式中：n系为导航坐标系，p系为导航坐标系，φ为捷联导航数学平台姿态角误差，v，δv分别为捷联导航数学平台速度及其误差，ω，δω分别为角速度及其误差，f，δf分别表示加速度计测量比力及其误差；δg为重力偏差，为 从p系到n系的 方向余弦矩阵。

对于长航时旋转调制惯导系统，陀螺和加速度计的常值漂移、安装误差等引起的系统误差可以被调制成常值，不会引起随时间发散的误差。陀螺G 效应误差、比例因子不对称性、磁场、器件随机游走等引起的误差无法被精确补偿，会引入随时间发散的误差［12］，是长航时惯导系统需要关注的重点。如图1 所示，以陀螺G 效应误差为例，0.000 5（°）/h 的陀螺G 效应误差3 天内会引起0.4 海里的定位误差，且该误差无法通过旋转调制进行补偿，需要采用其他方法进行有效的辨识和标定［13-14］。此类误差通过旋转调制无法精确补偿，引起的误差产生等效的东向陀螺漂移和北向陀螺漂移，在长航时导航时其误差传播主要体现为经度误差随时间缓慢发散，对长航时导航的精度有显著影响。

图1 陀螺G 效应误差引起的导航误差Fig.1 Navigation error curves caused by G-sensitive drift of laser gyro

2.2 误差自标定基本原理

惯导系统自标定将陀螺常值漂移、标度因数误差、安装误差和加速度计零偏、标度因数误差、安装误差设为状态变量，建立30 维卡尔曼滤波器状态方程：

其中：X(t)为状态向量，A(t)为系统状态转换矩阵，G(t)为系统噪声输入矩阵，W(t)为系统噪声向量。状态向量取为：

其中：φ为状态误差，δV为速度误差，δL，δλ，δh分别为纬度误差、经度误差和高度误差，ε，为陀螺常值漂移，ΔSg，ΔSa分别为陀螺和加速度计的标度因数误差，ΔMg，ΔMa为陀螺和加速度计的安装误差。

系统状态转换矩阵表达式为：

式中：ωie为地球自转角速率，VE，VN，VU分别为东向、北向和天向速度，L为纬度，h为高度，RM，RN分别为地球子午圈、卯酉圈的曲率半径。

乡村旅游的持续发展，能够有效激活乡村闲置资源，改善乡村基础设施，提升贫困人口的自我发展能力。在旅游电子商务快速发展的背景下，乡村旅游与精准扶贫融合是乡村振兴的绿色之路，两者深度融合发展已成为新时代发展新业态的新手段。现实意义主要体现在：

系统噪声输入矩阵为：

系统噪声向量为：W(t)=，其中Wgx，Wgy，Wgz分别表示陀螺输出噪声，Wax，Way，Waz分别表示加速度计输出噪声，均视为高斯白噪声。

以速度误差和位置误差为观测量建立卡尔曼滤波器的观测方程：

3 对准导航标定旋转路径一体化设计

为保持长航时旋转调制惯导系统精度的长期稳定性，通常选用较长的对准时间，典型如4，6，16 小时等。以6 小时初始对准为例，为提高导航精度，在每次初始对准过程中，先利用前2小时进行惯导系统误差参数的自标定，通常采用18 次序旋转路径精确标定惯性器件的安装误差、比例因子误差等，利用标定的误差参数转入4 小时初始对准，对准结束后再转入导航状态，这样利用刚标定的误差参数进行对准和导航，可以消除安装误差、比例因子等长时间参数缓慢变化引入的导航误差，提高对准的效果和导航精度［10］。

本团队提出了一种48 次序对准导航标定一体式旋转路径，具体方案如图2 所示。图中U，E为导航坐标系的天向轴和东向轴，A～D，A＇～D＇为8 个停滞位置，虚线表示常值漂移矢量ε在旋转过程中的运动轨迹（初始位置为A），1～48 表示48 个旋转次序，每个次序旋转90°。该方案绕水平两轴进行翻转，与目前广泛采用的16 次序［15］旋转方案不同的是增加了旋转90°的位置，既可以有效调制惯性器件误差，又可以提高标定过程中的可观测度。

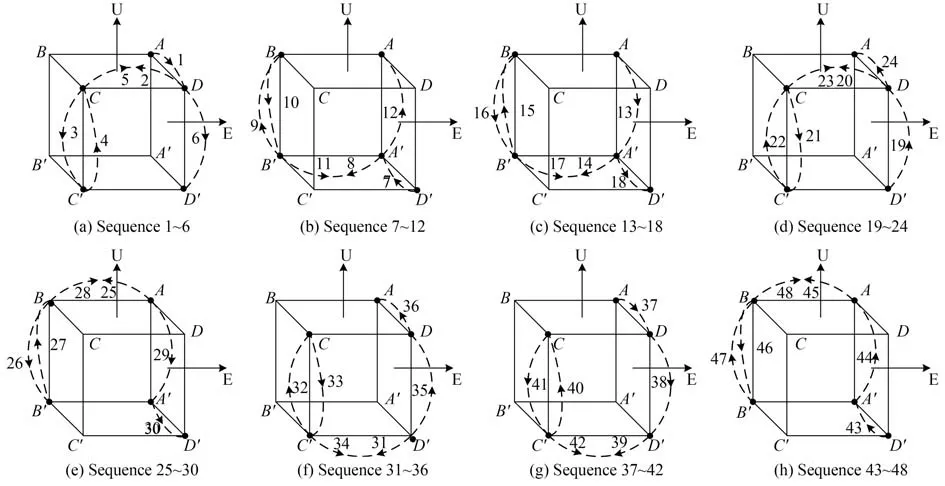
图2 48 次序一体式旋转方案示意图Fig.2 Unified 48-sequence rotation scheme

按照此旋转方案，可以实现惯导系统自标定、自对准与旋转调制一体式设计，对准过程中可以实现惯导系统误差参数的精确标定和高精度初始对准，导航过程中可以实现误差参数的自动平均和补偿，从而实现旋转路径的完全统一［14］。

4 基于重复样本的惯导系统长周期导航测试

4.1 测试方法设计

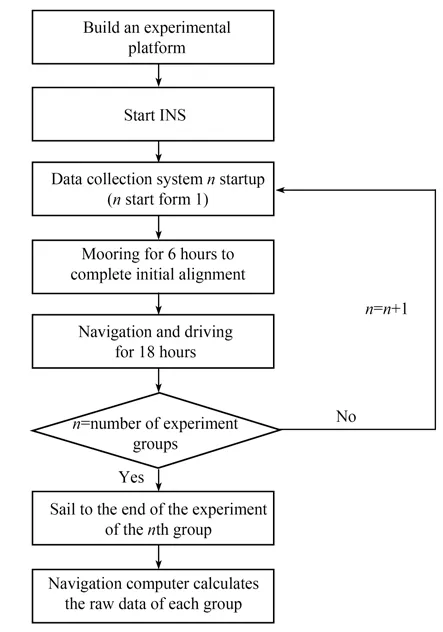
图3 长周期导航测试方法实施流程Fig.3 Flow chart of long-endurance navigation test

整个实验测试装置包括：试验船、被测试的长航时惯导系统、基准信息系统、惯性元件数据采集系统和导航解算计算机。基准信息系统可以包括但不限于卫星导航设备、惯性/天文、卫星组合导航设备等，用于实时确定载体的姿态、位置和速度信息。惯性元件数据采集系统可同时采集激光陀螺和加速度计的原始脉冲输出、基准信息系统输出的姿态、位置和速度信息。舰船运动路径及方案如图4 所示。

图4 八组导航实验过程中载体运动状态Fig.4 Carrier motion state during eight navigation experiments

假设导航实验组数为n，每组导航实验所需天数为N，则设置n套惯性元件数据采集系统，每一套惯性元件数据采集系统分别负责采集对应次序的导航实验的原始数据。该方法步骤如下：

（1）将长航时旋转调制惯导系统安装在试验船平台上，启动惯导系统和基准信息系统，按照本文提出的转位方案对惯导系统进行旋转调制；

（2）试验船保持停泊状态6 小时，使被测试惯导系统完成导航实验1 的自标定和初始对准：包括自标定2 小时，初始对准4 小时；以初始对准开始时刻作为导航实验1 的采样起点，惯性元件数据采集系统1 开始采集被测试惯导系统中激光陀螺和加速度计的原始脉冲输出、基准信息系统输出的载体姿态、位置和速度信息；

（3）完成导航实验1 的初始对准后，试验船进入航行状态，航行状态可以选择匀速直线运动、匀加速/匀减速直线运动、圆周运动、不规则曲线运动等运动方式或这几种运动方式的随机组合，航行18 小时后到达任意停泊点；

（4）试验船进入停泊状态，停泊状态保持6小时，期间按照与步骤（2）中相同的初始对准方法完成导航实验2 的初始对准，以导航实验2 的自标定和初始对准开始时刻作为导航实验2 的采样起点，惯性元件数据采集系统2 开始采集被测试惯导系统中激光陀螺和加速度计的原始脉冲输出、基准信息系统输出的载体姿态、位置和速度信息，由于此时导航实验1 并未结束，这些数据同时由惯性元件数据采集系统1 和惯性元件数据采集系统2 采集，因此可同时作为导航实验1 和导航实验2 的共用数据，包括导航原始数据，即代入导航解算的激光陀螺和加速度计的原始脉冲输出、基准信息系统输出的载体姿态、位置和速度信息；

（5）重复步骤（3）～（4），直到第n组导航实验的初始对准阶段结束后，试验船进入持续航行状态，航行状态可以选择匀速直线运动、匀加速/匀减速直线运动、圆周运动、不规则曲线运动等运动方式或这几种运动方式的随机组合，直到第n组导航实验进行到第N天时，航行结束；

（6）使用导航解算计算机分别处理n组导航实验的被测试惯导系统中激光陀螺和加速度计的原始脉冲输出，基于捷联惯导系统姿态、速度和位置更新算法计算得出n组导航实验的纯惯性导航姿态、速度和位置信息，将纯惯性导航位置、速度信息与基准信息系统输出的载体姿态、位置和速度信息进行比较，评估惯导系统导航测试结果。

n组导航实验的舰船运动状态与初始对准时刻的停泊目的地均可以不同，这就保证了多组导航实验采样的充分性。将n组N天长周期导航实验的总时长压缩至n+N-1 天，极大地节省了长周期导航测试的时间和资源成本。以8 组导航实验的周期30 天为例，实验实施如图5 所示。

图5 八组导航实验中实验数据采集时序Fig.5 Time sequence of experimental data acquisition during eight navigation experiments

4.2 实验验证

为验证实验方案的有效性，利用实验室研制激光陀螺惯导系统进行了实验室测试，实验现场如图6 所示。将惯性测量单元置于转台上，依据设计好的旋转路径开展自标定、对准和导航试验，对准时间为6 小时，进行了一次37 天的长周期导航实验，第1 天到31 天的第一航次、第2 天到32 天的第二航次、第7 天到37 天的第八航次导航结果如图7 所示。为方便比对，将论文所有实验数据的定位精度进行了归一化处理，8 组导航实验定位精度结果统计如表1 所示。

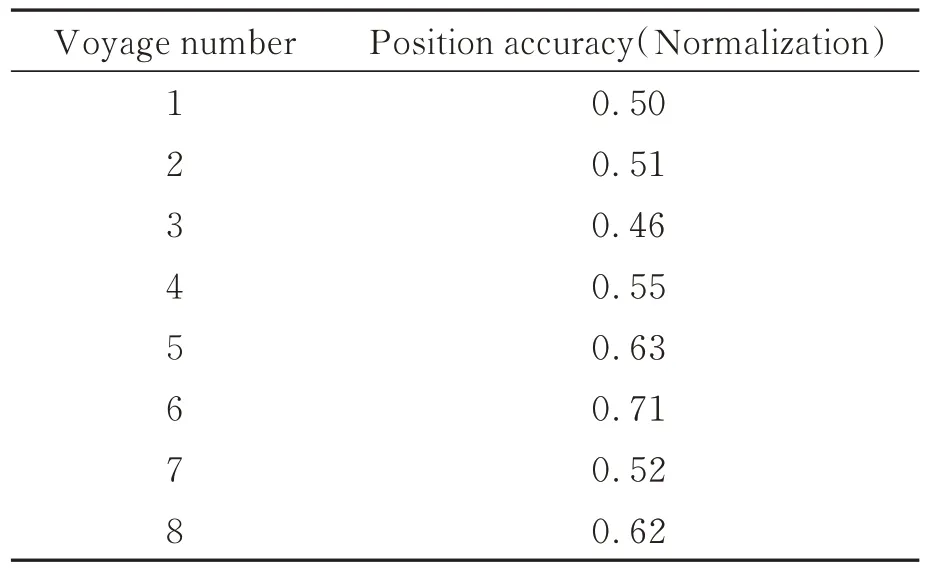
表1 37 天导航实验中8 个航次的统计结果Tab.1 Statistical results of 8 voyages in 37 days navigation test

图6 长航时导航验证实验Fig.6 Long-endurance navigation verification test

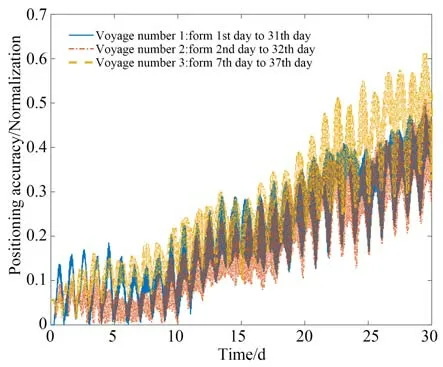
图7 37 天导航实验中3 个典型航次定位误差曲线Fig.7 Position error curve of three typical voyages in 37 day navigation test

为了比对测试评估方法的可行性，在2021 年3 月至2022 年6 月，对激光陀螺旋转惯导系统进行了8 个航次单独启动的长航时导航实验，每个航次的启动时间均为6 小时，每次实验的周期为30 天，随机抽取部分航次进行对比分析，其中航次1，2，6 的实验曲线如图8 所示，8 个航次的实验统计结果如表2 所示。

表2 8 个独立航次实验的统计结果Tab.2 Statistical results of 8 independent voyages

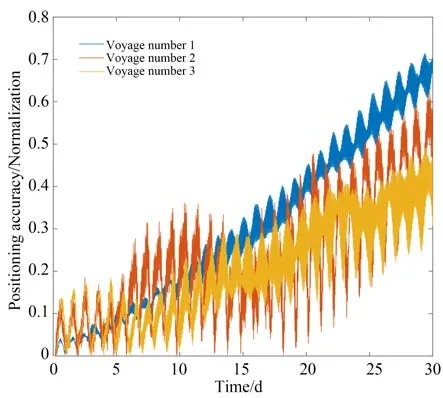
图8 8 个独立航次中3 次典型实验结果Fig.8 Position error curve of 3 typical tests in 8 independent voyages

为充分验证方法的有效性和可行性，对惯导系统进行了车载动态实验，受实验条件和时间的限制，在长沙周边地区开展了为期5 天的车载动态导航实验，实验平台及航行曲线如图9 所示。

图9 动态试验平台及运动轨迹Fig.9 Test vehicle and track for dynamic test

依据设计好的旋转路径开展自标定、对准和导航实验，对准时间为6 小时，每个航次的导航时间为72 小时，选取第1 天到第3 天为第一航次，选取第2 天到第4 天为第二航次，选取第2 天车辆静止时刻进行第2 航次的6 小时初始对准，选取第3天到第5 天为第三航次，选取第3 天车辆静止时刻进行第3 航次的6 小时初始对准，直至实验结束，实验结果如图10 所示。

图10 3 次车载导航实验结果Fig.10 Results of three vehicular navigation tests

从长航时静态及短航时车载动态实验可以看出，重复利用导航数据和与独立进行实验对惯导系统的性能统计结果一致，该实验测试评价方法对长航时惯导系统的精度评价具有一定的普适性和可用性。通过1 个37 天的导航实验可以充分验证8 个航次的30 天长航时导航实验精度，极大地缩短实验测试时间。

5 结论

本文针对旋转调制惯导系统长航时实验测试和评估方法开展研究，在自标定、自对准和旋转调制导航旋转路径统一的基础上，提出了一种基于重复样本旋转调制惯导系统测试评估方法。该方法充分利用长航时导航过程中的导航信息，大幅缩短了实验周期，同时考虑了载体运动的机动性和多样性。利用实验室样机进行了周期为30 天的长航时导航实验验证，定位精度的最大值为0.71（归一化），与独立航次多样本实验精度基本相当。利用短时车载动态实验验证了方法的有效性，后续将深入开展长航时惯导系统误差传播特性研究，增加姿态、速度等精度考核，开展系泊、航行实验验证，以充分验证方法的有效性和可行性。