基于拓扑优化的电渗流微混合器电极

孙建文，张健宇，李博文，邓永波*

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049）

1 引言

微流控系统具有高通量、分析时间短、样品消耗率低等优势，已广泛应用在生物、化学和医药等领域［1-3］。微混合器是微流控技术中主要的功能器件，根据驱动方式不同可分为被动混合器和主动混合器。与被动微混合器通过改变微通道几何形状或添加几何障碍物来增强混合效果不同［4-5］，主动微混合器通过施加外部能量来扰动样品，具有更短的混合时间，并且操作者可根据具体情况对混合器进行开关操作［6］。

电渗驱动是主动微混合器中一种常用的驱动混合方式，其工作原理是通过对微通道流体施加外部电场产生电渗流动现象，达到不同浓度溶液混合的目的。Matsubara 等通过交错的电极排布来增强非定常微流体的混合效果［7］。Seo 等研究了环形微混合器的电极位置对混合性能的影响［8］。Xiong 等利用收敛和发散原理设计一种菱形电渗微混合器，并通过改变菱形角度与组合方案，研究了电极电压、电极结构和雷诺数对混合性能的影响［9］。Farahinia 团队对微通道壁面非均匀分布电极电渗微混合进行研究［10］，随后将电渗流与压力流相结合开展进一步研究［11］。Lv 等针对非牛顿流体与牛顿流体的微混合展开研究，验证两种流体混合效果与电压频率成正比，与入口流速成反比［12］。Chen 等提出一种能够快速响应并且充分混合的交流电场微混合器结构，并对混合单元、电极对数等参数进行讨论分析［13］。上述工作通过改变微混合器结构、电压、雷诺数以及电极排布方式等影响因素提高了样品的混合效率，然而缺乏对电渗流微混合器电极版图的结构设计研究。

电渗流是在双电层、外部电场与流场相互作用下生成的。因此，施加外电场的电极版图对控制电渗流起关键作用。为提升电渗流微混合器的混合性能，可对微混合器的电极版图进行拓扑优化设计。拓扑优化能够在缺乏设计经验的情况下，找到满足设计目标与约束条件的材质最佳分布，从而确定结构的最优拓扑。

针对上述问题，本文研究了电渗流电极的拓扑优化方法，以实现两种不同浓度溶液的完全混合为设计目标，建立电渗流微混合器模型，进而确定微混合器的电极版图，并通过改变电压、混合单元设计方案等影响因素验证微混合器的混合性能，得到混合效果最佳的设计方案。

2 模型建立

在微混合器中，电渗是由与电解质溶液接触的微通道壁表面上净电荷集聚所产生的。电荷聚集在壁面形成双电子层［14］，其厚度远小于微流体的特征尺寸（通常为10 nm），可将其近似为滑移壁面。因此，电渗微流体可以用具有滑移壁面边界条件的Navier-Stokes 方程来描述，其中滑移速度满足Helmholtz-Smoluchowski 公式：

式中：u与p分别是流体速度和压力；V是电极受到的外部施加电势；ρ和η分别是电解质溶液的密度以及动力黏度；μeo=-εrε0(ξ0/η)为 电渗迁移率，εr，ε0和ξ0分别是相对介电常数、自由介电常数以及zeta 电位；n是∂Ω上的向外单位法线。

如图1 所示，电渗微混合器示意图由入口通道、混合单元（混合设计区域）和出口通道组成。其中，Ω为微混合器设计域，Γia∪Γib=Γi为微混合器入口，Γo为出口，Γw和Γd是微混合器壁面。电极版图在Γd所示混合单元上下壁面进行设计，上表面为施加电压的阳极，下表面为接地阴极，V0为阳极所受电压。微混合器模型满足Γi∪Γw∪Γd∪Γo=∂Ω。电渗流微混合器特征尺寸l∝100 μm，混合单元半径R=n·l，其中n为混合单元的半径系数。

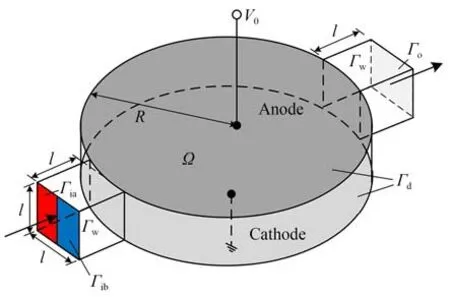
图1 电渗微混合器示意图Fig.1 Schematic diagram of electroosmotic micromixer

在电渗流微混合器中，影响混合效果的两个主要因素为扩散与对流。因此，两种不同浓度流体的电渗流混合可以用对流扩散方程进行描述：

式中：c是浓度，D是质量扩散系数。如图1 所示，两种不同浓度的溶液进入微混合器，其浓度设定为：

式中：ci是电渗微混合器入口处的已知浓度分布。微混合器壁面与出口的浓度场边界条件为：

电渗流混合器模型所受的外部电势可用Laplace 方程-∇·(σ∇V)=0 描述，σ是电导率。如图1 所示，在电渗流微混合器模型中，壁面边界被分为两部分Γw与Γd。Γw为电绝缘边界，Γd为混合单元电极设计区域。为了区分模型中的两种边界，将它表示为取值在［0，1］之间的物理密度的插值，其中0 和1 分别表示电势与电绝缘边界。因此，电极的设计区域的边界条件可以表示为电绝缘与电势的插值：

式中：V0施加电极电压；α为该方程惩罚因子［15］。

式中：γfp，αmax与q分别是物理密度变量、惩罚参数，以及用于调节惩罚凸度的参数。当模型的物理密度为0 时，在式（6）中，αmax取值足够大，以确保式（5）中的(V-V0)占据主导，使等式左侧-(σ∇V)·n项被忽略为0，即电极受到的电压V=V0，此时壁面为电势边界；而当模型物理密度为1 时，惩罚因子为0，式（5）可以转化为-(σ∇V)·n=0，即电绝缘边界。基于数值实验，αmax与q分别选择1×103与1×10-3。此外，在电渗流模型的入口与出口也施加为电绝缘边界。因此，电渗微混合器中电极受到的外部电势可以描述为：

物理密度变量是由定义在Γd上的设计变量通过Helmholtz 滤波器调整计算的［16］：

式中：γ是设计变量；γf是经过过滤的设计变量；∇s在Γd上局部坐标系定义的梯度；r是滤波半径，用于控制电极版图的特征尺寸；ns是在Γd向外的单位法线。在过滤计算后，使用阈值法去除过滤后的设计变量中0 与1 之间的中间值，并导出物理密度：

式中β与ξ是投影参数。

此时，电渗流模型的电极设计已转变成求解0-1 的最优材质分布问题。本文的目标函数为模型出口处的实际平均浓度与预期浓度之间的归一化最小二乘方差。电渗流微混合器的设计目标是通过找到合理的电极版图设计，达到不同浓度流体的有效混合。因此，模型变分问题可构造为：

约束条件下：式中Ψ0是出口处所测得浓度与理想目标浓度之间的最小二乘方差。

3 敏度分析

本文使用数值迭代的方法解决模型的变分问题。根据从等式的变分方程中提取的梯度信息，对设计变量进行最优化求解。基于对流扩散方程、Navier-Stokes 方程、Laplace 方程和Helmholtz 滤波器的伴随方程的弱形式，通过约束优化问题的偏微分方程对变分问题进行伴随分析：

式中：λf与λQ是拉格朗日乘子系数，用于在模型入口出口施加边界条件；λc为入口浓度边界条件的拉格朗日乘子系数；ca，ua，pa，Va，γfa，λfa，λQa和λca分别是其所对应状态变量的伴随变量；是其对应伴随变量的测试函数；H(Ω)和L2(Ω)分别是定义在Ω的一阶Hilbert 空间与二阶 Lebesgue 可积空间 ；H-1/2(Γw∪Γd)是迹空间H1/2(Γw∪Γd)的对偶空间；H(Γd)是定义在Γd的一阶Hilbert 空间；R 表示实数域。为了求解Navier-Stokes 方程和对流扩散方程，采用有限元法、广义最小二乘法和流线逆风Petrov-Galerkin（SUPG）法。Ne是离散化Ω的有限单元数；τgls和τsupg为稳定参数：

式中：hi表示的是在第i个计算域Ωi的大小。式（10）变分之后的一阶伴随导数为：

（1）用当前设计变量求解PDE 约束；

（2）基于PDE 约束的解求解伴随方程；

（3）计算优化目标函数的伴随导数；

（4）使用移动渐近线法计算并更新设计变量；

（5）检查迭代结果是否满足收敛准则，满足则变分计算结束；若不满足，将返回（1），继续迭代计算。

在电渗微混合器模型变分问题的收敛过程中，连续5 次迭代的目标函数变化满足第k次迭代步骤中的，或者达到已设定的最大迭代次数300 时，迭代结束。其中Ψk是第k次迭代的目标函数。在迭代计算中，式（9）中的阈值参数ζ设为0.5；投影参数β初始值设置为1，每40次迭代后加倍，直到最大值128。

4 数值实验

如图1所示，不同浓度的溶液从微通道入口流入到混合单元腔体内进行混合，并从微通道出口流出。在微混合器中实现混合的物理过程主要是扩散与对流，二者可通过改变流经微混合器流体的佩克莱数（Pe）与雷诺数（Re）进行调节。其中，U为模型入口处的平均速度，D为质量扩散系数。当Pe≫1 时，影响混合的主要因素为对流，反之即为扩散。而流体的对流强度是由Re表征的，。当Re≫1 时，对流在微混合器中起主导作用，反之黏性作用为主要作用。

模型数值实验的具体参数如下：电解质浓度ρ=1×，动力黏度η=1×10-3Pa·s，介电常数εr=80.2，电导率σ=0.12 (Ω·m)-1，Zeta 电势ζ0=-0.1 V。电渗流微混合器入口和出口微通道的特征尺寸l=4×10-4m，混合单元半径R=n·l。

微混合器选取V0=4 V，n=2，l=4×10-4m，Pe=1×103和Re=1，对式（10）进行迭代计算求解。

为直观展示模型的混合性能，将目标函数Ψ作为混合评价指数，其数值与混合效果呈负相关关系。当混合评价指数小于0.05 时，两种不同浓度的溶液已完全混合［17］。

图2 是拓扑优化模型设计变量的演化过程。当迭代300 次后，电渗流微混合器与混合单元表面电极版图如图2（f）所示，黑色区域表示优化设计后的电极布局。图3 是目标函数的收敛过程，其逐渐收敛平稳的趋势可表示该拓扑优化方法的稳定性。

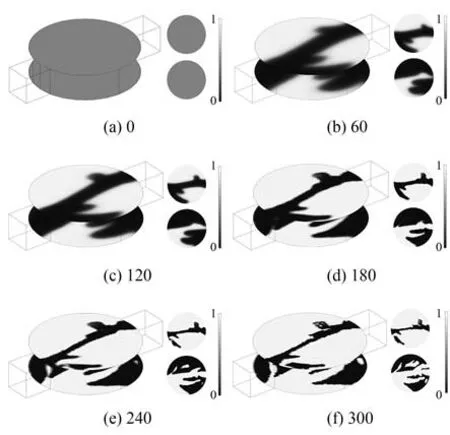
图2 电渗流微混合器物理密度演化过程Fig.2 Physical density evolution of electroosmotic flow micromixer

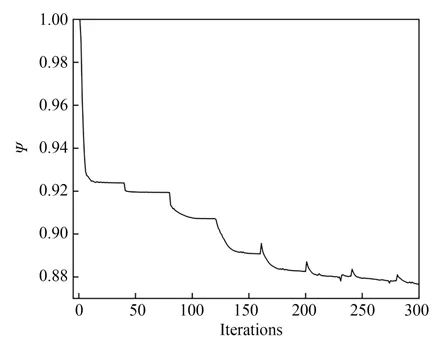
图3 拓扑优化目标函数的收敛过程Fig.3 Convergence history of optimization objective function values

为验证电极拓扑优化微混合器的混合性能，将未进行电极设计的微混合器与电极拓扑优化微混合器的混合效果进行对比，如图4 所示。结果表明，未进行电极设计的微混合器混合作用主要以扩散为主，在低雷诺数下只有较弱的平流，致使微混合器的混合性能大幅降低；而经过电极拓扑优化的电渗微混合器可对不同浓度流体进行有效混合。

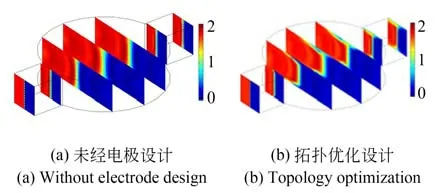
图4 微混合器浓度截面对比Fig.4 Concentration cross section comparison of micromixer

本文考虑影响微混合器混合性能的因素，通过改变混合单元设计方案、施加电压、混合单元特征尺寸、雷诺数和佩克莱数等参数，研究它们对电渗流微混合器混合效果的影响，验证电极拓扑优化方法的有效性。

4.1 多混合单元设计

由于电渗流微混合器的混合单元体积较大，在混合溶液时，存在混合不充分的现象。因此采用多混合单元（N）的设计方案，通过增加混合驱动路径的长度来提高溶液的混合性能［13，18］。

图5 为N=9 时微混合器电极版图和不同混合单元方案（N=1，…，9）的出口浓度分布。从图5 中N=9 模型截面浓度分布可知，不同浓度溶液进入微混合器后，溶液流经多个混合单元，混合效果随混合驱动路径的增加逐渐叠加，在出口处浓度分布呈现有效混合。从图5 和图6 可知，溶液混合效果随混合单元数量的增加而增强，当N=9 时，混合评价指数达到0.05 以下，上述结果证明该方案可满足不同浓度溶液的完全混合［17］。

图5 多混合单元（N=9）的电极版图和不同混合单元模型方案的出口浓度分布Fig.5 Electrode layout of mixing units（N=9）and outlet concentration distribution of different mixing unit model schemes

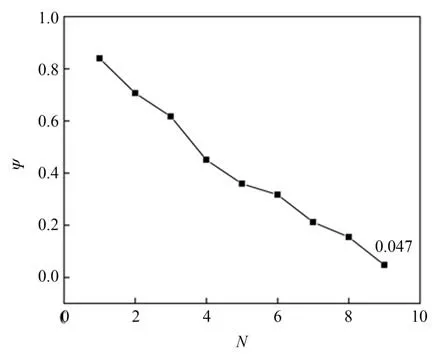
图6 不同混合单元模型方案的混合评价指数Fig.6 Mixed evaluation index of different mixed unit model schemes

本文继续讨论微混合器混合效果的影响因素，从而验证微混合器的混合性能。为便于后续数值模拟，采用单个混合单元微混合器方案进行分析讨论。

4.2 电极电压的影响

电极电压是影响电渗流微混合的主要因素之一。这里在保持其他参数不变的情况下，将施加电压V0分别设置成1，2，3，4 和5 V，讨论施加电压对电渗流微混合器混合效果的影响。图7 为不同施加电压下得到的电极设计布局和出口浓度分布，图8 是分别对应的不同施加电压下的混合评价图。根据图7 和图8 可知，较高电势会产生更强的电场，在电渗流微混合器中有效引起扰动以及对流，从而得到更好的混合效果，有效提升微混合器的混合性能。

图7 不同施加电压电极版图和出口浓度分布Fig.7 Electrodes obtained by applying different voltages and export concentration distribution

图8 不同施加电压混合评价指数Fig.8 Mixed evaluation of different applied voltages

4.3 混合单元特征尺寸的影响

将微混合器混合单元半径R作为特征尺寸，R满足R=n·l，其中l=4×10-4m。图9 为改变控制半径系数n后所得的电极设计布局与出口浓度分布。从图10 可知，混合评价指数与模型混合单元特征尺寸的关系，当n从1 逐渐增到3 时，微混合器的混合驱动区域逐渐增大，混合效果也随之增强。

图9 不同半径电极版图和出口浓度分布Fig.9 Electrode and outlet concentration distribution obtained by different radii

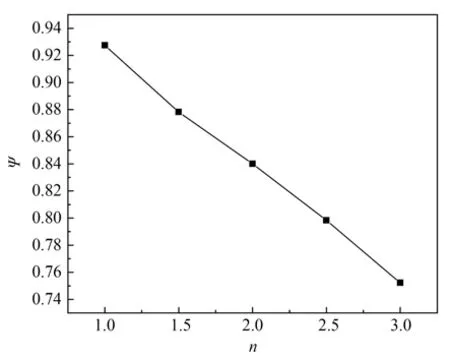
图10 不同半径混合评价指数Fig.10 Mixed evaluation of different radii

4.4 佩克莱数与雷诺数的影响

佩克莱数的物理意义是对流速率与扩散速率的比值。从图11 和图12 可知，电渗流微混合器在保持Re=1 的情况下，佩克莱数越低，混合效果越好。雷诺数是流体力学中表征黏性影响的相似准则数，在微通道流体流动中，不考虑湍流的影响时，雷诺数主要表征对流的程度。在保持佩克莱数不变时，低雷诺数时混合过程主要受到扩散的影响，拓扑优化设计的电极布局所产生的电渗流动可以加强流体的横向流动，以此加强混合效果，如图13 所示。

图11 不同佩克莱数下的电极版图和出口浓度分布Fig.11 Electrode and outlet concentration distribution obtained by different Pelect numbers

图12 不同佩克莱数混合评价指数Fig.12 Mixed evaluation of different Pelect numbers

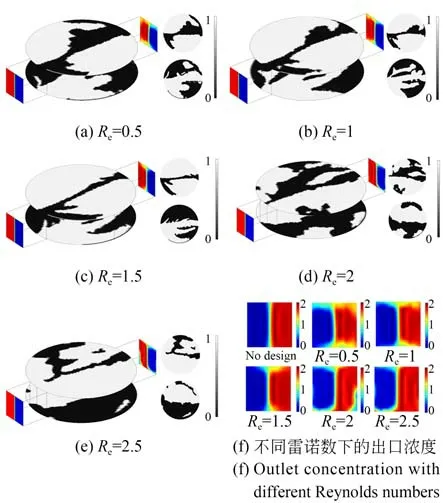
图13 不同雷诺数电极版图与出口浓度分布Fig.13 Electrode and outlet concentration distribution obtained by different Reynolds numbers

当微混合器内流体雷诺数逐渐升高时，流速的增加导致两种不同浓度溶液在混合器中的混合时间减短，致使微混合器的混合效果不佳，如图14 所示。

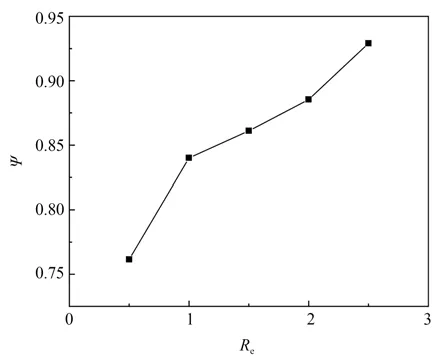
图14 不同雷诺数混合评价指数Fig.14 Mixed evaluation of different Reynolds numbers

5 结论

本文基于拓扑优化方法，以加强微流体混合效果为设计目标，通过在微混合器壁面施加电绝缘与电势的插值的方法，建立电渗流微混合器模型，设计优化电极版图。数值模拟结果表明，电渗流微混合器的混合评价指数在多混合单元（N=9）设计下可达0.047，满足完全混合的预期效果，从而验证本文设计方法的合理性。本文构造了由Navier-Stokes 方程、对流扩散方程所约束的变分问题，引入Helmholtz-Smoluchowsk 将双电子层进行近似约束处理，采用基于拉格朗日乘子的伴随方法和基于梯度信息的迭代方法对变分问题进行分析和求解。该电渗电极设计方法摆脱了经验设计的限制，在化学与生物等领域具有潜在的应用价值。