考虑角度偏差的压电三维力传感器标定

张 军，王郁赫，任宗金，孙文举，蔡佳乐

（大连理工大学 机械工程学院，辽宁 大连 116024）

1 引言

多维力传感器广泛用于机器人［1-2］、航空航天［3］等领域，用于力和力矩的测量与反馈，其测量精度直接影响装备性能。基于石英的压电力传感器具有高刚度、动态特性好和耐高温等特点，适于强振动、大温变等恶劣工况［4-5］下高频动态力的测量，在大型精密装备研发中起着重要作用。

在使用前，力传感器需经标定获取其灵敏度参数［6］，包括主向灵敏度和耦合灵敏度，用于测量与解耦，其标定精度一般取决于标定模型与标定装置精度。标定模型一般采用改进传统矩阵方法［7］和机器学习［8］方法，以提高标定精度。Yu［9］等针对机器人腕力传感器采用旋转标定方法以减少安装偏差带来的精度损失。李映君［10］等采用径向基函数神经网络改进了力传感器标定算法。田雨［11］提出基于深度置信网络的压电多维力传感器标定解耦方法。此外，标定装置的角度偏差也会使传感器在标定中损失精度［12］。付立悦［13］等从不确定度角度指出加载力源偏角是砝码张线式装置标定误差的主要来源。范志强［14］等分析了压电薄膜式力传感器在标定中安装基面倾角带来的精度影响。上述研究表明，标定中安装和加载带来的角度偏差会影响标定精度，导致获取的传感器参数不准确。为了减小标定角度偏差的影响，研究多集中于精度评定和装置精度提高［15］，但精度提升的成本较高。对于削弱和分离角度偏差引入的误差，则缺乏相关研究。

本文改进了传统标定模型，分析标定角度偏差来源与影响并引入标定模型，以组内自制压电式三维力传感器为研究对象，采用实际测量+优化算法的方法获取了传感器的真实性能参数，有效分离了角度偏差的影响。解耦效果证明，改进的新标定模型更贴合实际数据。最后，基于新模型分析了标定角度偏差对传感器耦合特性的影响。

2 原理

2.1 传感器结构与偏差来源

压电石英三向力传感器一般包含3 组晶组，每组包含2 片石英晶片。两组Y0°晶组基于剪切效应测量Fx和Fy，一组X0°晶组基于纵向效应测量Fz，实现正交三维力测量。标定传感器时，为了标定侧向力（Fx，Fy），通过螺栓和螺母将传感器预紧在上下压块间形成标定结构，如图1 所示。预紧力一般是侧向力的10 倍，保证传感器通过摩擦感受足够的侧向力。

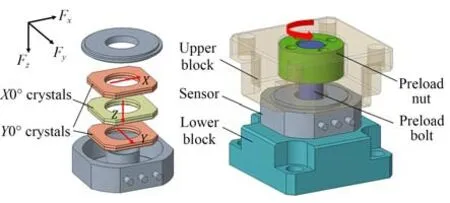
图1 压电传感器与预紧标定结构Fig.1 Piezoelectric sensor and preload calibration structure

对于多维力传感器，一般在不同测量方向分别进行单维力标定，逐步获取每个方向的灵敏度。理想情况下，标定力源的加载方向与传感器的测量敏感轴完全共线。而标定角度偏差，例如加载偏斜、安装偏角等，会使二者存在夹角，降低主向灵敏度，增大了耦合灵敏度（横向灵敏度）。对于图1 所示坐标系下的力传感器，偏差来源如图2 所示。在传感器预紧成标定结构时，夹具固定上下压块，力矩扳手施加预紧力，带动传感器相对上下压块转动［16］，敏感轴绕Z轴转动，如图2（a）所示；固定基面不平，传感器倾斜，敏感轴绕X/Y轴转动，如图2（b）所示；标定装置加载力源偏斜，对其他非标定方向产生附加分力，如图2（c）所示。

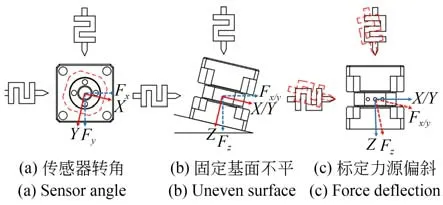
图2 标定角度偏差来源Fig.2 Sources of calibration angle deviation

为叙述方便，以绕轴顺时针旋转为正，用x表示传感器的敏感坐标系绕X轴转动的角度，y，z同理，用θab表示b方向加载力源对a方向的偏角。

2.2 装置偏差测量

以实验室的三维力加载装置和力传感器为对象，测量图2 中偏差值。

测量传感器转角时，下压块固定在台面上，将精度为0.02 mm 的数显千分表打在传感器侧面，推动传感器移动29 mm，千分表示值差为0.11 mm，通过反正切函数测得z为+0.22°，如图3（a）所示。

图3 传感器转角与基面倾角测量Fig.3 Measurement of sensor angle and base angle

测固定基面倾角时，将精度为0.1°的倾角仪紧贴单元与底面，通过读数读取倾角值，测得x为+0.5°，如图3（b）所示，同理测得y为-0.4°。

测量力源倾斜偏角时，以测量X向加载偏角为例，倾角仪1 为0 时，一方向读取倾角仪2 示数，测得θzx为-0.15°；另一方向将千分表垂直打在测量处，加载杆向前移动距离，根据千分表示值差求出θyx为-0.13°，如图4 所示。其他方向偏角测量同理。

图4 标定力源偏角测量Fig.4 Deflection measurement of calibration force source

为方便后续的计算处理，将测量角度值单位换为弧度制（rad），测量结果如表1 所示。

表1 角度偏差测量Tab.1 Angle deviation measurement （rad）

结果表明，传感器标定中确实存在角度偏差，理论上标定精度会降低。

2.3 标定模型改进

压电力传感器受力产生电荷，电荷经放大器转为电压信号。由于使用的石英压电系数不同，Y0°晶组灵敏度是X0°晶组的两倍左右，实际中电荷放大器会将它们归一化为-1 附近的力电系数。为了便于比较，这里使用力电系数代表传感器灵敏度。

传统标定模型如下：

其中：U为输出电压向量，K为力电系数矩阵，F为标定力值向量，kab为力电系数。当a=b时，为该向主向力电系数；当a≠b时，为b对a的耦合力电系数。

考虑标定角度偏差下，K为带有偏差的力电矩阵，F也不是标准的正交标定力源，用Kr代表真实的传感器矩阵，FI代表理想正交的标定力源。

z的测量基准为千分尺所固定的面，即为下压块，相当于自转或相对转动，而x，y的测量基准为大地坐标系（出厂校准的倾角仪）。在旋转矩阵中左乘代表绕大地坐标系旋转，右乘代表绕自身坐标系旋转，用旋转矩阵R1与R2修正传感器的力电矩阵，得到K与Kr的关系：

其中：

考虑角度较小，旋转矩阵采用简化形式。以X向加载标定为例，产生的Z向干扰力为：

将公式推至3 个方向，则得到F与FI的关系：

其中：

式中：lx，ly，lz分别代表x，y，z主方向的加载系数，理想下均为1。将式（3）与式（5）带入传统模型式（1），建立新模型：

其中：Kr即为真实的传感器力电系数矩阵，去除了角度偏差影响，U是采集的电压，FI是理想的正交加载力，力大小可通过标准力传感器测得。

新模型共有21 个参数，x，y，z和θab在2.2 中已测得，lx，ly，lz可由勾股定理求解，剩余9 个力电系数为未知量。考虑测量仪器和方法的精度较低，采用优化算法，首先通过实验获得U，再根据数据建立合理的目标函数与约束条件，以测量值为优化起点，给予参数一定的变化范围，获取传感器参数。

3 标定实验与参数获取

3.1 标定实验

在2.2 的基础上继续实验，标定装置配备MCL-S 型标准力传感器，放大器为联能LN5861，采集卡为DT9800，软件为DEWESOFT，如图5 所示。传感器Z向量程为12 000 N，X，Y向量程为2 400 N。根据划好的中心线，在传感器中心分别对3 个方向加载阶梯力，记录输出，得到传感器3 个方向的电压输出如表2～表4 所示。加载过程中，采用仪器复测表1 中的参数，参数无变化，测量后卸载。

表2 X 向加载输出数据Tab.2 X-directional load output data

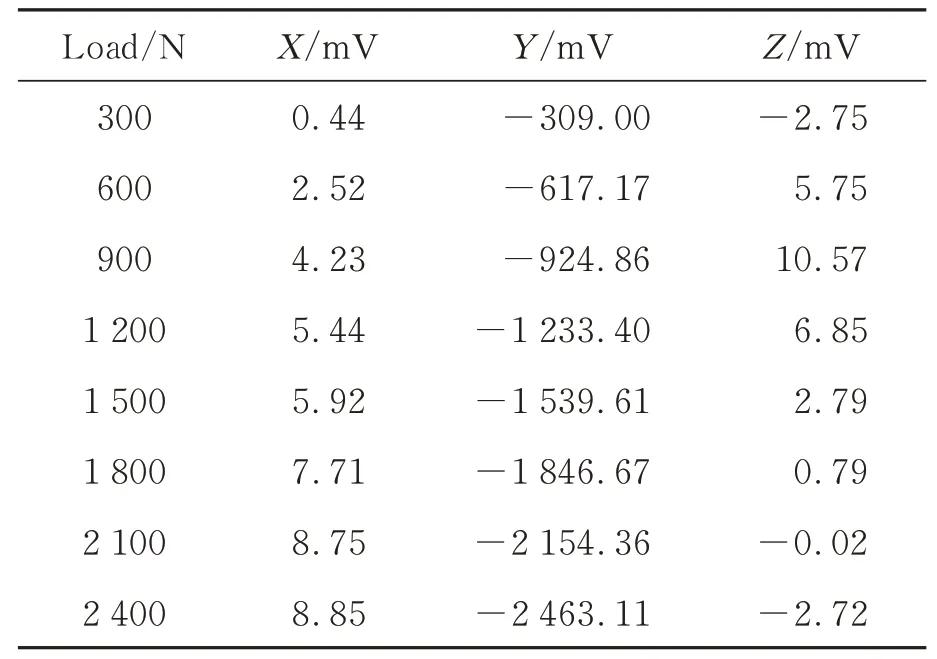
表3 Y 向加载输出数据Tab.3 Y-directional load output data

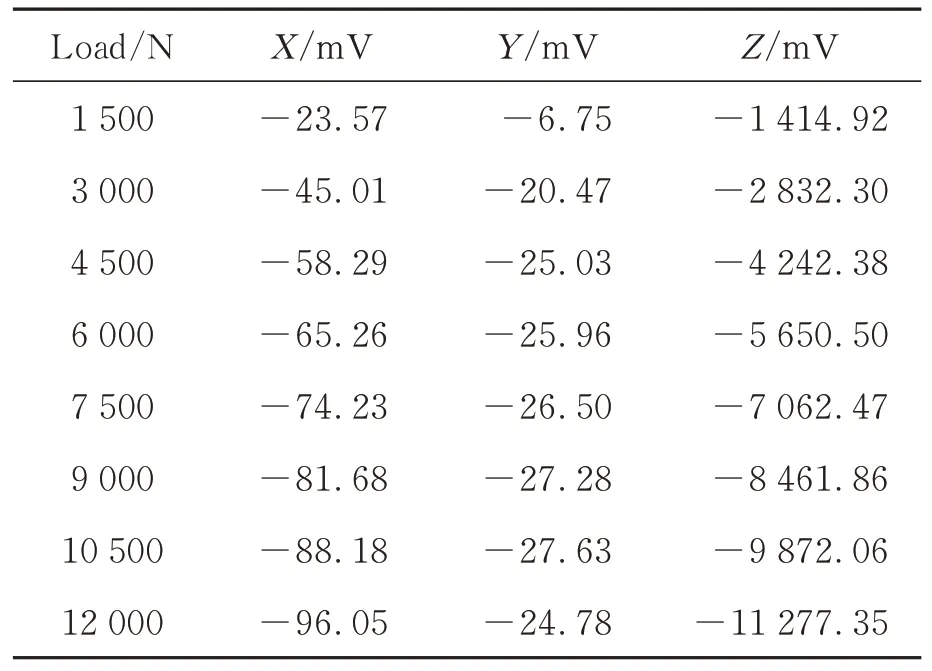
表4 Z 向加载输出数据Tab.4 Z-directional load output data

图5 力传感器标定设备Fig.5 Equipment for calibration of force sensor

3.2 参数获取与比较

传统参数获取方式是采用最小二乘法分别拟合3 个输出方向对单输入方向的直线斜率，从而求得主向和耦合力电系数。新模型增加了角度矩阵，参数数量较多，难以采用上述方法求解。由于摩擦和加载振动等原因，数据掺杂随机误差，所以采用优化算法求解。为了尽量避免局部最优解，加入约束条件。

优化模型包括设计变量、目标函数和约束条件3 个步骤，设计变量即为式（6）中的21 个参数。

目标函数采用文献［17］中基于极大似然法建立函数，即：模型输出与实际数据差的二范数平方和越小，模型越贴合数据。根据表2～表4得到：

约束条件如下：

（1）受限于测量仪器和方法的精度，根据倾角仪测量精度0.1°，将表1 测量值作为参数优化起点，限制范围为±0.002 rad，弥补测量精度不足，同时一定程度上也能避免局部最优解。

（2）单方向加载系数平方和的根应在1 附近，以满足勾股定理，考虑实际加载和采集有一定偏差，平方根限制为1±0.01，如式（8），避免不合理参数。

算法选择斯坦福大学开发的稀疏非线性优化求解算法（Sparse Nonlinear Optimizer，SNOPT），其核心是基于序列二次规划优化算法，适合于解决各类规划问题，可集成于MATLAB 和COMSOL 等计算软件。该算法处理实际大规模问题时的计算速度比一般智能算法快，且收敛性好［18-19］。

考虑到配合压电传感器使用的电荷放大器灵敏度设置位数一般到小数点后3 位，为了保证精度，同时缩短收敛时间，将优化容差（停止阈值）设置为0.000 1，最小化目标函数Q以求解21个参数。所有参数连续3 次迭代差值小于阈值时即认为收敛，经过12 次优化，计算收敛。

R1，R2，C的求解结果如下：

力电系数的优化求解过程如图6 所示。

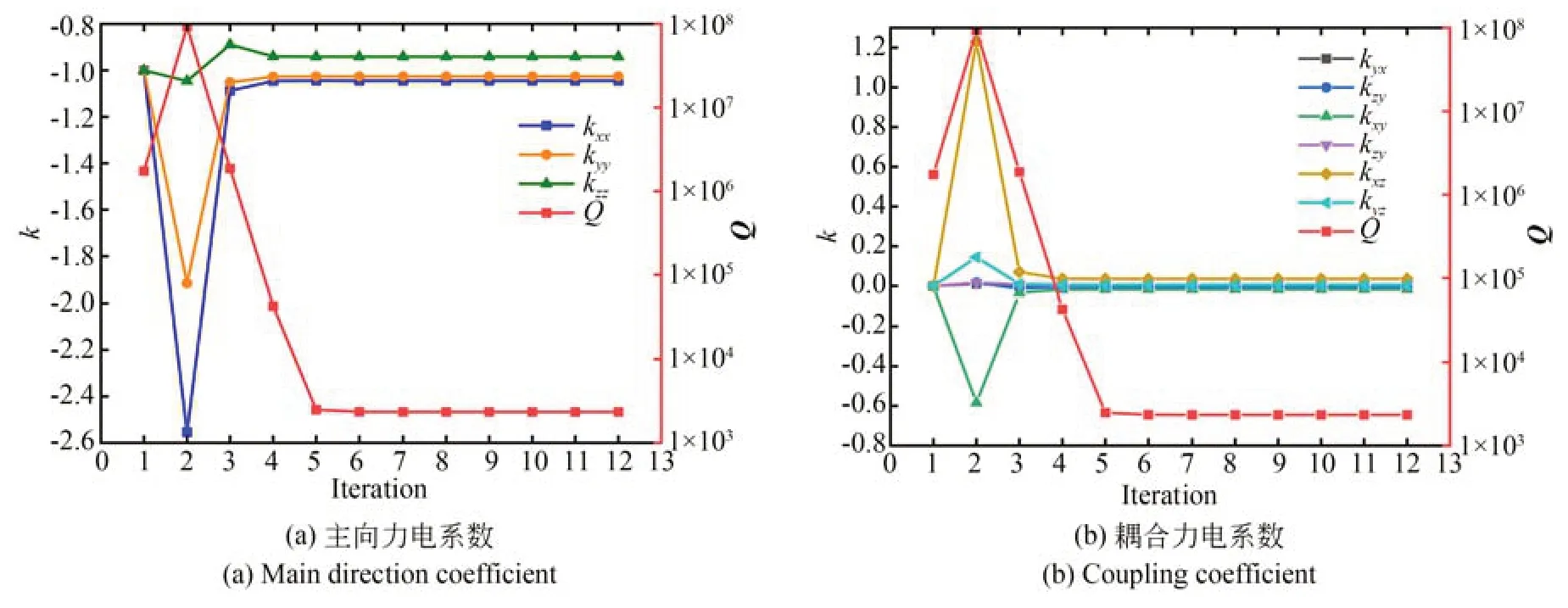
图6 参数求解迭代过程Fig.6 Parameter solving iterative process

将分离偏差前后力电系数，即K与Kr的元素进行对比，见表5～表6。角度偏差对主向力电系数标定的影响较小，但对耦合力电系数的影响较大。由于偏差存在，部分耦合力电系数的变化较大甚至反向，会获取虚假的系数，导致传感器性能评定的谬误。

表5 耦合力电系数比较Tab.5 Comparison of coupling coefficients

表6 主向力电系数比较Tab.6 Comparison of main direction coefficients

4 模型效果对比与分析

4.1 解耦效果对比

理论上如果模型贴近传感器的实际情况，应更贴合实验数据，解耦误差更小。为验证新模型的合理性，采用两种模型对实验数据进行解耦，即将表中3 个方向的加载力值代入模型，比较模型计算的电压输出与表中记录的电压输出间的差值，如图7 所示。

图7 解耦误差比较Fig.7 Decoupling error comparison

用解耦误差的均值、极值进一步比较，以旧模型的解耦误差为基准，分析新模型相比其解耦误差下降的比例，如表7～表8 所示。

表7 解耦误差均值下降比例Tab.7 Decoupling error mean reduction ratio（%）

Y向加载时，X向耦合输出的解耦误差没有下降，因其原本耦合输出较小，新旧模型的解耦差值几乎重合。而从其他方向的均值来看，解耦误差减少了80% 左右，极值减少了20%～49%。结果显示，新模型更吻合实际数据，验证了新模型的正确性。新模型矩阵相乘后仍为3×3 矩阵，在降低解耦误差的同时没有增加复杂性。

4.2 耦合系数占比研究

由于结构与制作原因，多维力传感器难免具有耦合灵敏度，精确测量耦合灵敏度或解决耦合问题［20］是研究焦点。由于标定角度偏差会影响传感器的耦合特性，将传感器转角和固定基面倾角合称为安装偏差。根据新标定模型，每个偏差影响矩阵均已知，分析安装偏差与力源偏斜偏差两种因素对耦合力电系数的影响占比，具体步骤如下：

（1）将R1KrR2C作为所有角度偏差作用下的标定结果A；R1KrR2表示仅受安装偏差影响的标定结果B；KrC表示仅受标定力源偏斜影响的结果C；

（2）将B 与C 的耦合系数元素分别与真实结果Kr相应元素做差，求得安装偏差和力源偏斜对耦合系数的影响数值。

（3）将Kr元素和（2）影响数值除以A 中对应元素，求得耦合系数下的传感器自身、安装偏差和力源偏斜的数值占比。

理论上矩阵间为乘法，会叠加影响，不应加减。但由于角度较小，经过验算，Kr与两个因素影响差值和与A 各项差不到0.000 1，可以忽略。如图8 所示，标定角度偏差对于传感器耦合性能的影响不可忽略，在部分耦合系数中，标定角度影响占比达到70%以上，应加以控制。本次标定中，力源偏斜主要影响了X，Y向对Z向力的耦合系数，而安装偏差主要影响了X，Z向对Y向力的耦合系数。

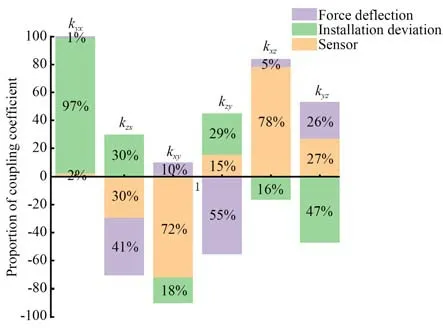
图8 耦合力电系数占比分析Fig.8 Proportion analysis of coupling coefficients

5 结论

本文针对力传感器标定角度偏差影响精度的问题，以压电三向力传感器为对象，相比旧标定模型与传统参数获取方法，建立了考虑标定中多环节角度偏差的新模型，并通过测量和优化计算结合获取参数，基本实现了分离角度偏差的传感器标定。新模型大部分方向的解耦误差均值下降80%左右，极值下降20%～49%，验证了新方法有效性。

研究表明，一般被当作标准力源的标定装置，其偏差会影响传感器的标定精度，尤其会在耦合灵敏度的标定中引起谬误，放大或缩小真实的灵敏度。从标定精度角度，如何控制或者给出偏差容差范围，给出标定装置的精度检定标准，值得进一步研究。经矩阵维数推广和数量增加，本文模型可推广到六维力传感器或测力仪的标定中，覆盖更多影响因素。