纳米级运动轨迹规划和控制

李爱琳，李 璟*

（1.中国科学院 微电子研究所，北京 100029；2.中国科学院大学，北京 100049）

1 引言

集成电路（Integrated Circuit，IC）制造在先进制程芯片的生产中占有非常重要的地位［1］。近年来，由于工艺制程的缩短，对IC 制造装备产率和精度的要求不断提高。作为IC 制造装备的重要子系统，工作台通常采用直线电机-气浮/磁浮式导轨驱动结构和激光干涉-镜面反射测量系统来实现高速、高加速运动和纳米级运动定位精度［2-3］。但气浮/磁浮导轨使工作台在运动摩擦力近似为零的同时也导致工作台对振动敏感，这有悖其快速准确定位的要求［4］。针对这一问题，人们从改进控制器［5-8］、优化参考轨迹［4，7，9-12］等方面着手进行研究。

控制器的改进目标是减小系统在工作区间的运动定位误差。运动定位误差有多种来源，包括多自由度耦合误差、跟踪误差等。工作台的多自由度耦合误差一般通过力学补偿解耦和控制系统补偿两步消除［13］：力学补偿解耦即通过补偿策略消除各轴之间的力学因素耦合［7，14］，如驱动电机的出力点和测量系统的测量点（Point of Interest，POI）不一致带来的耦合误差；力学补偿解耦后残余的耦合误差（由驱动电机出力不稳定、制造安装等导致的运动误差）一般可进行矢量场正交分解，再通过控制系统实时补偿，控制系统通常采用对各轴独立设计单输入单输出控制器的策略［6，13］。

除多自由度耦合误差外，由参考轨迹和外部扰动引起的跟踪误差也是控制系统动态误差的主要来源之一。为减小跟踪误差，Dai等设计了一种加速度+参考轨迹三阶导+参考轨迹四阶导的多项式前馈控制器［5］，能有效减小系统建立时间，但仅对前馈控制器的性能进行改进难以满足工作台纳米精度的定位要求。目前，工作台的反馈控制器多采用比例-积分-微分（Proportional Integral Derivative，PID）控制［5，7，15-16］，根据经验在线调试3个参数，但在线调试需要耗费大量时间试凑。差分进化算法具有良好的全局搜索能力，能根据当前搜索情况动态调整搜索策略［17-18］。将差分进化算法应用于PID 控制器的参数整定中，可在给定范围内自动寻找符合优化目标的控制参数。

除了改进控制器之外，对参考轨迹进行合理规划也有助于提高工作台的性能［12］。工程中常采用的参考轨迹分为梯形运动轨迹（二阶）和S型运动轨迹（三阶及以上）。梯形运动轨迹算法实现简单且具有良好的快速性，但运动过程中被控对象的加速度会发生突变［4］，对机械结构造成冲击，进而激发振动，导致系统建立时间增加，影响运动定位精度。为改善上述问题，Roover 等［15］提出使用边缘平滑的S 型轨迹来实现最小振动下的点对点运动，Pizza 等提出通过约束轨迹的三阶导来提高运动的平滑度［5］，并通过实验验证［11］了该方法能有效降低被控对象加减速造成的冲击以及设备的机械磨损。虽然Roover 和Pizza 提出的轨迹规划算法提高了系统定位精度，但均未考虑参考轨迹对控制器的要求。轨迹规划所考虑的阶次越高，轨迹轮廓越平滑，对系统机械结构的冲击越小，然而高阶轨迹对控制器实时处理的数据量和处理速度的要求更高，控制器的设计难度随之增加［19］。另一方面，上述轨迹规划算法均未考虑如何确定轨迹的动力学约束，通常是由设备情况推算轨迹动力学约束的范围，然后试凑出具体值。由于动力学约束的可选范围很广，手动试凑的工作量大。蒙特卡洛算法作为已经被广泛应用的一种数值计算方法，是以概率统计理论为基础，通过模拟随机变量来解决数学问题中的非确定性［20］。将蒙特卡洛算法应用于轨迹运动学约束的参数整定，可以提高调参效率。

本文提出了一种应用于工作台的轨迹规划优化方案。该方案以工作台为被控对象搭建相应的控制系统，在驱动电机的出力点和测量系统测量点不一致等引入的耦合误差可进行矢量场正交分解的前提下，考虑在控制回路中加入补偿策略，并通过差分进化算法自动整定控制器参数；其次，在进行轨迹设计时考虑控制器的实际跟踪效果，并根据应用需求和设备情况确定轨迹的动力学约束后，运用蒙特卡洛算法迭代优化出符合控制器性能和应用场景的参考轨迹。最后，通过仿真和实验验证了所提轨迹规划方案的有效性和合理性。

2 轨迹规划方案

为提高工程调试的效率和运动定位精度，本文提出的轨迹规划方案如图1 所示。根据设备情况得出驱动电机参数及布局、机械系统所能承受的最大冲击等信息，结合应用场景确定轨迹动力学约束的范围，再由应用需求确定系统优化目标。根据系统优化目标改进控制器，并考虑控制器的实际跟踪效果，进行参考轨迹的优化。

图1 本文提出的轨迹规划方案Fig.1 Proposed trajectory planning scheme

2.1 应用场景与研究目标

现代集成电路对晶圆制造设备的量产要求是产能达到每小时280 片晶圆［6］，对运动系统的挑战就是需要同时满足高时效性和纳米级重复定位精度。根据现有验证平台的工程实际需求，本研究预期运动定位系统在力学补偿解耦的情况下，按照0.4 s 内完成一次一维参考轨迹跟踪的要求，并保证重复性定位精度达到约±5 nm/3σ。

2.2 系统优化目标

工作台的单个运动周期可以用S 型轨迹描述，理想S 型运动轨迹通常可划分为加速、匀速、减速区间三部分［12］。实验发现，工作台高加减速结束时刻存在的残余能量会激发机械结构的振动，所以将匀速区间继续划分为稳定区间（残余振动区间）和工作区间（扫描区间），如图2 所示。在稳定区间内控制器需要将跟踪误差收敛到可接受范围ε内（一般要求ε在纳米甚至亚纳米量级），才能使工作区间内设备精细加工操作的精度满足系统要求。

图2 工作台的单个运动周期Fig.2 Individual motion cycle of stage

工作台在理想工作区间内的跟踪误差的均值（Moving Average，MA）和标准差（Moving Standard Average，MSD）能反映工作台的运动定位精度［7］。本文将MA 和MSD 两个指标作为系统优化目标，并采用ISO230-2 标准评价工作台的重复定位精度。

3 控制系统简化模型

3.1 六自由度控制系统的数学模型

工作台控制系统的简化模型如图3（a）所示，r表示参考轨迹(r，r＇，…，r(n))中的位置指令，控制系统（包括前馈控制器FF 和反馈控制器GC）根据测量系统解算出的位置out 和位置指令r之差计算控制信号uPOI。根据第1 节描述，驱动电机出力点和测量系统测量点不一致造成的力学因素耦合误差在纳米精度的定位系统中不可忽略，控制信号uPOI需要经过补偿矩阵G，质心受力-控制信号转换矩阵Q，以及位置变换矩阵R后才能转换为POI 受力fPOI。控制信号uPOI与fPOI之间的转换关系为：

图3 工作台控制系统的简化模型Fig.3 Simplified model of stage＇s control system

补偿策略的目的是能够把根据POI 位置计算得到的控制信号完全转化为POI 受力，即R·G=I。

从控制器的角度而言，被控对象的传递函数为：

其中：Ga=Diag {Gax，Gay，Gaz，Gaθx，GaθY，Gaθz}指工作台在POI 处的六自由度模型，如图3所示［5-7］。

以地面某固定点O为原点定义六自由度的参考坐标系(x，y，z，θx，θy，θz)。图3 给出了测量系统测量点POI 和驱动电机出力点Oc的相对位置。在集成电路制造的工艺过程中，POI 位于工作台上表面且随参考轨迹变化，而驱动电机的出力点为工作台质心Oc。根据POI 位置与参考位置之差计算出的控制信号uPOI经过补偿矩阵G转换为控制信号uc。uc经过出力分配后转换成每个电机驱动器接收到的电压指令，驱动器内部的电流环在接收到电压指令之后输出对应大小的电流驱动工作台运动。工作台属于过驱动系统，对同一自由度上的驱动电机出力进行合并后得到Oc处受力fc（fc=fx1+fx2），上述过程用质心受力-控制信号转换矩阵Q表示，Q为6×6 的常值对角矩阵，由电机的布局方式、出力分配策略和电机参数（电压-电流转换系数、推力常数）决定。Oc处受力(fc)还需经过位置变换矩阵R得到POI 受力(fPOI)，R代表Oc与POI 的相对位置关系，由参考轨迹决定。

记POI 在参考坐标系下的测量位置为(xm，ym，zm，θxm，θym，θzm)，POI 和Oc均位于工作台上，根据刚体变换可以导出控制信号uPOI到uc的转换关系［7］：

其中：m表示工作台的质量，h表示Oc和POI 沿z方向的距离，Jx，Jy，Jz分别表示θx，θy，θz方向的转动惯量，通常根据名义值或系统辨识获得。

在本文的应用场景下，运动系统在x方向和y方向需要跟踪参考轨迹进行一维扫描，扫描过程中z方向会有微小位移，θx，θy，θz方向一直处于定位控制状态，所以做以下近似：θz≈0，θ＇z≈0（其余两个自由度同理），结合式（3）导出六自由度补偿矩阵G：

其中：I表示单位矩阵，G的第1～6 行行向量分别对应6 个自由度方向(xm，ym，zm，θxm，θym，θzm)的力学耦合补偿分量。

根据第1 节描述，当G的设置使得各自由度之间的力学耦合误差可以忽略，控制器的设计及补偿就能针对各轴分别开展［6，13］。

3.2 单自由度控制系统的数学模型

以x方向为例对单自由度上的被控对象进行建模。由于实际系统中不同元件之间的连接并非理想的刚性连接，被控对象采用non-collocated 形式的双质量块柔性体模型［5，8，16］，如图3所示。图中，fPOI表示POI 处受到的电机驱动力；m1表示x方向的驱动电机动子的质量；m2表示用于精密定位的镜面系统的质量；out 表示由激光干涉仪测量解算得到的系统在x方向的位置；k和c分别表示m1和m2在x方向的等效连接刚度和等效连接阻尼，二者可以与系统的结构阻尼比ζ、结构的谐振频率ω相互转换。系统的传递函数为：

对超精密系统的位置控制器而言，由机电设备引起的延时不可忽略。考虑到电机驱动延时、信号传输延时等因素，模型中引入延时τ，得到控制器角度下被控对象在x方向的数学模型：

其中：Qf-u为常数，表示x方向Oc受力与控制信号之间的转换关系。

理想单自由度扫描运动的补偿分量为式（4）中补偿矩阵G对应的行向量，单自由度参考轨迹r的数学模型会在后文进行推导。

根据图3，若忽略扰动的影响，控制系统的跟踪误差为：

控制目标为error →0，所以前馈控制器应当尽量逼近被控对象的逆模型：

本文中前馈控制器也采用多项式前馈的形式uff(t)=β1r(2)(t)+…+βn-1r(n)(t)［5，7-8］，且uff(s)=FF(s)·r(s)。由于四阶参考轨迹有r(5)≡0，取式（6）右侧前4 项（k=3）代入式（8）得到前馈控制器的相关参数：

反馈控制器采用PID 控制［6-7］：

3.3 参考轨迹的数学模型

在实验场景下，运动系统在x方向和y方向上的跟踪参考轨迹要进行一维扫描，同时要保证扫描的稳定性和可靠性，即工作台的稳定性和重复性精度要高。在扫描过程中工作台需要跟踪预设参考轨迹完成点对点运动，具有动力学约束的n阶点对点参考轨迹位置指令r是由位置函数r(t)按周期Ts采样得到的，r(t)的一般形式为：

其中：αn由轨迹的动力学约束range 确定，r(n)表示参考轨迹的n阶导，δn表示常数，n阶轨迹r(n+1)≡0。

根据综合控制器的实时处理能力和跟踪精度，本文采用图4 所示的四阶参考轨迹（n=4），它由td，tj，ta，tv唯一确定，分别对应工作台处于最大加加加速度dmax、最大加加速度jmax、最大加速度amax和最大速度vmax的时间段。

图4 典型的四阶运动轨迹Fig.4 Typical fourth-order motion trajectory

综上，系统模型的相关参数组为：

其中：m1表示工作台沿x方向驱动电机动子的质量；m2表示工作台镜面系统的质量；τ表示系统延时；Ts表示系统采样周期；ω和ζ表示工作台的谐振频率和结构阻尼比；Jx，Jy，Jz表示工作台在θx，θy，θz方向的转动惯量，以上参数在实际调试过程中一般均可通过名义值或系统辨识获得。

控制器的相关参数组为：

其中：β1，β2，β3表示前馈控制器参数，可通过式（9）计算得出；kP，kI，kD表示反馈控制器参数，后续将给出反馈控制参数的获取方法。

4 轨迹规划方案的实施步骤

4.1 系统优化目标

在工作台跟踪参考轨迹进行一维扫描的过程中，图1 所述的系统优化问题可描述为：

其中：smax一般由扫描对象的长度确定；运动速度和加速度过大易引发系统的残余振动，一般在设备的说明手册中会给出vmax和amax的参考值；jmax和dmax由工作台机械系统所能承受的最大冲击决定，工程设定的经验值范围：20amax≤jmax≤50amax，20jmax≤dmax≤50jmax；为了减小环境变化（温度、湿度和洁净度）对精度的影响，要求单个运动周期不超过0.4 s。

根据系统优化目标对控制器和参考轨迹进行优化。反馈控制器的第一个设计目标是最小化系统的跟踪误差；第二个设计目标是最小化系统在高加减速结束后的残余振动，由于残余振动与运动轨迹的三阶导有关，这反映到控制上就是对控制信号的微分进行约束。所以PID 控制器的参数选择属于多目标优化问题，即有：

其中tend表示单个运动周期。

轨迹规划的第一个目标是减小控制器的跟踪误差；第二个目标是提高轨迹匀速区间的长度，使控制器有足够的时间调整系统加减速造成的冲击。

4.2 反馈控制器优化

使用改进的差分进化算法［18］对式（15）进行参数整定，整定步骤如图5 所示。

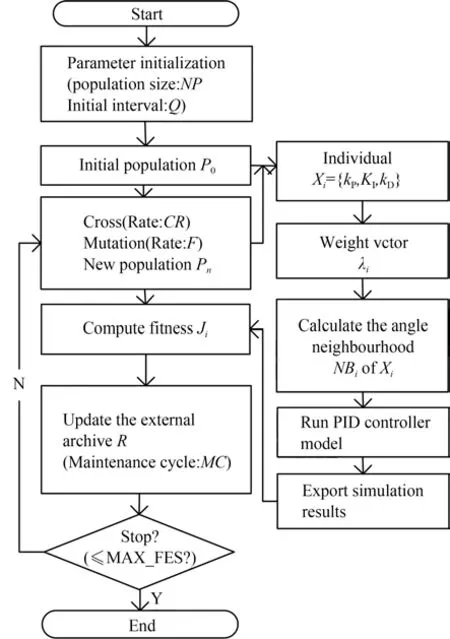
图5 使用改进的差分进化算法整定反馈控制器参数［18］Fig.5 Tuning feedback controller settings using improved differential evolutionary algorithm［18］

4.3 轨迹规划流程

轨迹规划希望所得轨迹的总运动时间短，工作区间占总运动时间的比例高。本文采用的轨迹规划算法流程如图6 所示，具体步骤如下：

图6 轨迹规划算法流程［4，12］Fig.6 Flow chart trajectory planning algorithm［4，12］

第1 步：根据图4，由轨迹的单个动力学约束分别确定td1，td2，td3，td4［4］，系统需要满足轨迹的所有动力学约束，td=min{td1，td2，td3，td4}。由于算法的计算机实现均为离散化处理，为了确保所得轨迹满足给定的动力学约束，需要将td向上圆整为采样周期Ts的整数倍tdr；

第2 步：将tdr和轨迹动力学约束一起作为已知参数，代入求得tjr；

第3 步：按照上述方式依次求得tar，tvr；

第4 步：根据图4，在得到tdr，tjr，tar，tvr四段时间之后就能得到r(4)(t)，按照不同的时间段对r(4)(t)依次向上进行数值积分，可以得到r(t)；

第5 步：将r(t)按周期Ts采样，得到参考轨迹r。

图6 算法流程的前提条件是轨迹的动力学约束参数值已给定，所以还需要在式（14）给出的约束空间中进行参数整定。由于动力学约束参数和轨迹之间的映射关系非线性，且每个约束参数的可选范围大，对轨迹性能的影响程度难以用单一方程进行描述，导致手动试凑约束参数组的工作量大。本文使用蒙特卡洛算法整定轨迹的动力学约束参数。整定的基本步骤为：

第1 步：参数初始化，初始边界由式（14）确定，初始约束参数组的数量为N，个体选取比例为ρ；

第2步：在边界内随机产生N组能生成可行轨迹的约束参数组rangei={smax，vmax，amax，jmax，dmax}i(i=1，2，…，N)，根据图6 得到相应的轨迹ri；

第3 步：采用图3 所示的控制系统进行轨迹跟踪。根据控制系统的输出outi，计算匀速区间的长度Li以及系统在工作区间的MAi；

第4 步：将{L1，L2，…，LN}按从大到小的顺序排列并按比例ρ(0＜ρ＜1)选取前W=ρ·N条轨迹，取这W组轨迹对应的约束参数组的上下限作为新的边界，同时记录W组轨迹中MA 最小的轨迹作为本次迭代的最优轨迹ribest；

第5 步：判断ribest和r(i-1)best是否相同，是则迭代结束，ribest为待求轨迹；否则返回步骤2。

综上，优化算法的相关参数组为：

其中：NP表示差分进化算法中的初始种群数量；Q表示差分进化算法种群个体的初始可调范围；F表示差分进化算法变异的比例因子；CR表示差分进化算法的交叉率；MC表示差分进化算法的维护周期；J如式（15），是差分进化算法中评价种群个体好坏的指标；MAX_FES是差分进化算法的结束条件，当有MAX_FES代最优个体的J相同时算法结束；N表示蒙特卡洛算法中的初始参数组数量；ρ表示蒙特卡洛算法中的选取比例。N和ρ的取值与优化结果和算法运行时间的关系如图7 所示。

图7 蒙特卡洛算法寻优结果与参数的关系Fig.7 Optimization results of Monte-Carlo algorithm with respect to parameters

图7（a）是在ρ固定(ρ=0.3)的前提下，运行30 次算法所得优化结果和运行时间的均值与N的关系；图7（b）是在N固定(N=103)的前提下，运行30 次算法所得优化结果和运行时间的均值与ρ的关系。可以看出，N和ρ的值越大，算法运行时间越长，若需进行在线轨迹规划，选取参数时需要权衡优化效果和运行时长。本文在使用蒙特卡洛算法整定轨迹的动力学约束参数时取N=104，ρ=0.3。

为验证算法的收敛性，图8 给出了蒙特卡洛算法的寻优结果分布。其中，方框是30 次蒙特卡洛算法优化出的动力学约束对应的跟踪效果分布；圆圈是随机生成30 组动力学约束对应的跟踪效果分布。图中蒙特卡洛算法的30 次寻优结果基本都收敛到相近解空间中，一定程度上验证了算法的收敛性。

图8 蒙特卡洛算法的30 次寻优结果分布Fig.8 Distribution of 30 times optimization result by Monte-Carlo algorithm

5 仿真及实验结果

参考实际的六自由度测试台得到式（12）中的系统模型参数，再分别使用传统工程调试方法和本文轨迹规划方案（见图1）计算参考轨迹和式（13）中的控制器参数，最后进行实验验证。

5.1 仿真及分析

在Matlab 中进行仿真，根据表1～表5 中的参数搭建图3 描述的控制系统。

表1 系统模型的相关参数Tab.1 Parameters of stage＇s model

本文轨迹规划方案所用优化算法的相关参数组见式（16），仿真取值见表2。

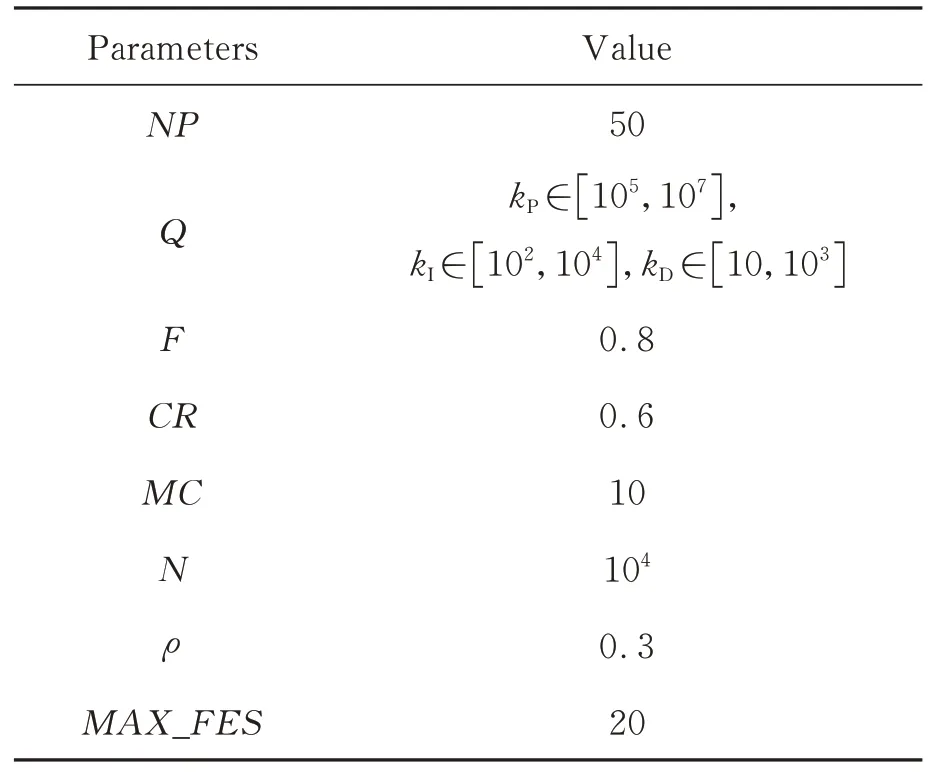
表2 本文优化算法的相关参数Tab.2 Parameters of proposed optimization method

将表1 参数代入式（9）可以计算出前馈控制器参数，再分别通过传统工程调试和本文差分进化算法（见图5）得到式（13）中反馈控制器参数。

传统工程调试方法整定PID 控制器参数通常为：使用Ziegler-Nichol 响应曲线法计算PID 控制器参数的初始值，根据该初始值确定参数可调空间Q，在Q内以最小化系统跟踪误差为目标进行在线调试，调试步长可根据经验设置，本文取ΔkP=104，ΔkI=102，ΔkD=102。

为对比两种方案对控制参数的整定效果，将算法从相同初始空间收敛到表3 中参数所需的迭代次数，作为方案的调参效率和收敛速度的评价指标。目标函数J（见式（15））在参数整定过程中的变化如图9 所示。

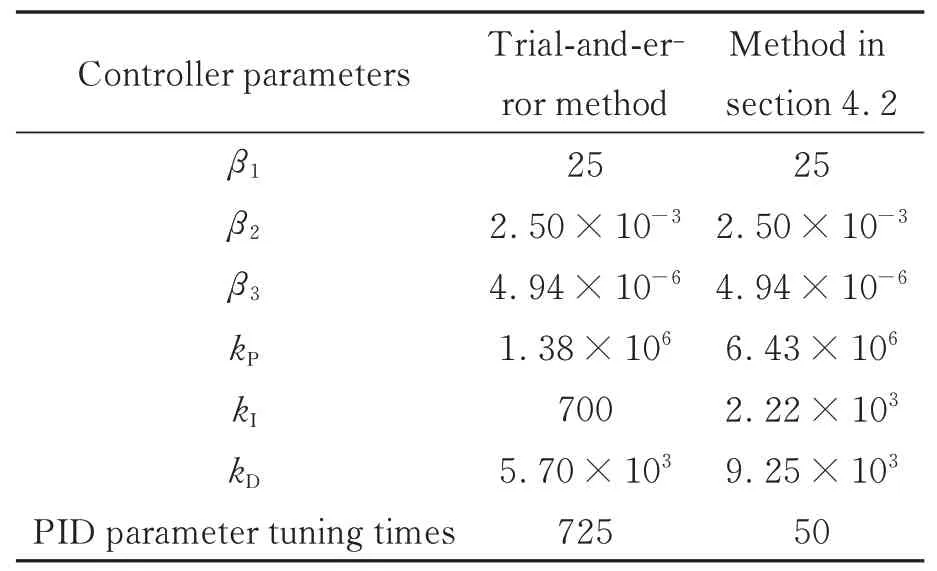
表3 控制器参数Tab.3 Parameters of controller

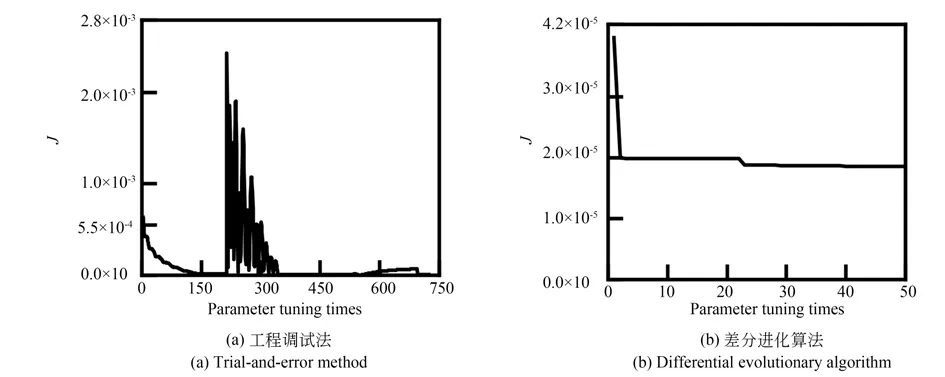
图9 两种方案的调参效率对比Fig.9 Comparison of tuning efficiency

由图9 可以看出，使用传统工程调试法进行控制参数整定的次数和效果依赖于工程经验；而差分进化算法能使种群向逼近最优解的方向自动迭代，可以提高控制器的参数整定效率。两种方案的控制参数见表3。

传统工程调试方法所得伺服系统的控制带宽为644 Hz，相位裕度为45°；使用差分进化算法所得伺服系统的控制带宽为627 Hz，相位裕度为30°。两种控制系统的性能基本一致，但差分进化算法的迭代次数减少了90%以上。

确定系统的控制器参数后，还需要确定参考轨迹。为对比两种方案的动力学约束参数整定效果，在仿真中模拟传统工程调试方法和蒙特卡洛算法（见4.3 节）分别进行3 次轨迹动力学参数整定，两种方案的初始计算域都为式（14），整定结果见表4 和表5。

表4 传统工程调试方法整定轨迹动力学约束Tab.4 Constraints of trajectory dynamics modified using trial-and-error method

表5 本文蒙特卡洛算法整定轨迹动力学约束Tab.5 Constraints of trajectory dynanics modified using Monte-Carlo method

表6 实验结果对比Tab.6 Comparison of experiment results

传统工程调试方法整定轨迹动力学的约束参数通常为：根据设备情况和应用需求推算出动力学约束范围后，根据整定经验，通过试凑确定参数的具体值。整定经验是：MA 主要与dmax，jmax，amax有关，总运动时间主要与vmax，smax有关，一般首先确定dmax的值，然后依次确定jmax，amax，vmax，smax。

从表4 和表5 可以看出，两种方案均能使系统在工作区间内的MA 收敛到3 nm 以内。传统工程调试法的整定次数和整定效果依赖于工程经验；而本文提出的轨迹规划方案通过设定优化目标，每一次迭代都缩小参数的可调范围，使算法朝逼近最优解的方向迭代。

相比传统工程调试法，本文方案保证控制器在工作区间内的MA 也收敛到3 nm 以内的同时，参数整定的次数还减小了90%以上，有效提高了工程调试的效率。

5.2 实验结果及分析

实际测试中，控制系统的简化模型和驱动电机的分布情况如图3 所示。对测试台在x方向的扫描运动进行轨迹规划，图10 给出了被控对象的系统辨识结果，其低频段-40 dB/dec 的幅频响应特性和445 Hz 左右的一阶谐振频率进一步验证了被控对象使用双质量块柔性体模型的合理性。测试平台的驱动电机采用音圈电机，其质心受力-控制信号转换系数Qf-u=169 N/V。

图10 测试台x 方向辨识结果Fig.10 Identification results in x direction of stage

用2.2 描述的系统优化目标评价由表4 和表5 中参数确定的轨迹，实验时分别取其中的最佳轨迹（表4 第1 次，表5 第3 次）作为系统的参考输入r，在100～400 μm 的一维行程进行重复扫描。采用前馈+反馈控制器进行轨迹跟踪，使用分辨率为0.15 nm 的激光干涉仪进行位置测量并计算工作台的运动定位精度。

图11 表明，同一控制器对本文轨迹规划方案得到的参考轨迹在工作区间内的最大跟踪误差为5 nm；而对传统工程调试得到的参考轨迹在工作区间内的最大跟踪误差为13.5 nm。

图11 实验结果对比Fig.11 Comparison of experiment results

实验结果表明，在控制器相同的情况下，两种方案得到的参考轨迹均能保证测试台的重复定位精度达到±5 nm 以内（ISO230-2标准下，传统工程调试法为 ±4.64 nm/3σ，本文方案为±3.76 nm/3σ）。本研究的简化模型目前考虑了由驱动电机的出力点和测量点不一致带来的耦合误差，实际应用中的运动定位误差会更加复杂。表4～表5 中的仿真结果基本印证了本文提出的轨迹规划方案在优化过程中可使跟踪误差快速收敛。

6 结论

本文针对多自由度工作台在加工过程中对参考轨迹的跟踪问题，提出了一种可提高工程应用中调试效率和运动定位精度的轨迹规划方案。该方案考虑了力学因素解耦在单轴分量控制回路中的补偿计算，使用差分进化算法自动整定反馈控制器参数，并考虑到应用场景需求和控制器的实际跟踪能力，运用蒙特卡洛算法迭代优化参考轨迹。该方案的重复定位精度达到±3.76 nm/3σ，该方案相比传统工程调试，在工作台重复定位精度均能达到±5 nm/3σ以内的前提下，控制器的跟踪误差能快速收敛，将参数整定过程的迭代次数减少约90%。

本文所述的轨迹规划方案的相关参数均可通过自动整定得到，能大幅减少调参过程的工作量，运用仿真和实验验证了大幅提升控制器精确调参效率的可行性。在此基础上，可进一步研究不同应用场景下多自由度运动的控制方案以及参考轨迹的实时在线规划，探索动态补偿策略。