三维点云深度模型压缩算法*

赵 志,许 可,马燕新,万建伟

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 气象海洋学院, 湖南 长沙 410073)

随着点云在自动驾驶、机器人、虚拟现实和增强现实等领域的应用需求不断增加,基于深度学习的点云网络模型得到了广泛的研究[1-9]。这些成果虽然取得了较为满意的结果,但耗时耗能耗资源的缺陷极大地限制了其在资源有限的移动端设备上的应用。所以如何使现有的深度模型真正落地应用是值得进一步探索的。虽然当前一些研究成果[7-9]在推理速度和存储上的性能有一定提升,但其仍然是基于昂贵的浮点数运算,占用了较多的计算资源。

网络量化作为模型压缩的一种重要方式,是解决该问题的有效途径,即把高位表示的权值或者激活值用较低位来近似表示,将连续的数值离散化,主要包括8位、4位、2位和1位量化。尤其对于1位,即二值量化,只存在两个数值-1(0)或+1,烦琐的矩阵乘法可以用简便的按位XNOR操作和Bitcount操作替代,可以实现最大的压缩比,进而最大限度地解决网络模型耗时耗存储的问题[10-18]。但二值量化的同时伴随的是精度的大幅度下降,如何提升二值量化网络模型的精度一直是国内外研究的热点,也是模型量化领域最具挑战性的问题。

当前关于模型二值量化的研究在图像领域研究较多,而在点云领域研究很少。包括BNN[16]和XNOR[17]在内的典型二值量化方法,在二维图像领域已得到了广泛的应用,表明二值量化具有重要的应用价值。而由于图像和点云之间存在的根本性差异,图像网络适用的二值量化方法并不能直接移植到点云网络上来。点云网络通过设计对称函数(如池化操作)来聚合点的特征以更好地处理点云的无序性。而不同于全精度网络,对于二值量化来说,池化操作较大程度地改变了隐藏层特征的统计特性,导致特征的可区分性下降较为明显。北京航空航天大学研究团队[19]提出的BiPointnet是近年来针对点云网络模型量化压缩研究的重要成果,通过设计最大熵聚合(entropy maximizing aggregation,EMA)模块和分层尺度恢复(layer-wise scale recovery, LSR)模块,尤其是最大熵聚合改善了池化层操作造成的特征同质退化问题,有效提升了全局特征的表示能力,较大程度地降低了量化导致的较大尺度变形。

当前,点云网络模型压缩的研究刚刚起步,仍存在较多的问题亟待解决。二维视觉模型量化压缩主要通过减小量化误差、减小梯度误差、改进损失函数以及改变网络结构等来提升性能[20]。目前对改进损失函数的研究主要包括给原损失函数添加蒸馏损失项[21-24]或非蒸馏损失项[25-28],其中,蒸馏损失是利用从全精度模型提取的信息来指导训练量化网络,可对中间层或softmax输出层进行蒸馏,而非蒸馏损失如激活分布损失[25]、通道相互作用损失[26]、增量量化损失[27]、损失感知量化[28]等,其中损失感知量化采用拟牛顿算法将与权重量化相关的总损失最小化。本文针对点云网络模型二值量化的问题,聚焦改善损失函数,首次将知识蒸馏方法[29-34]引入点云二值量化模型,设计点云深度模型压缩框架,考虑特征聚合问题引入了辅助损失项,改进的损失函数包括预测损失、蒸馏损失和辅助损失项。针对设计的损失项开展消融实验,对点云分类、部件分割以及语义分割不同任务进行对比实验。当前,用于点云全局特征聚合的最大池化也是大多数点云网络架构采取的流行设计方法[35],所以考虑算法的扩展性,在PointNet++[3]、PointCNN[4]和DGCNN[5]其他主流点云网络模型上进行拓展实验,以验证算法的有效性。

1 压缩模型

首先提出新的点云二值量化模型,进而分两个模块具体介绍蒸馏损失和辅助损失。

1.1 模型整体架构

如图1所示,模型主要包括教师网络、学生网络和知识蒸馏部分,其中教师网络即点云全精度网络,学生网络即点云二值量化网络,图中聚合(Aggregation)表示最大池化或最大熵聚合方法。通过引入全精度网络相关的软目标(Soft Targets)来诱导量化网络的训练,实现知识迁移,使得量化网络的性能更加接近全精度网络的性能。除蒸馏损失外,量化网络预测值与真实标签存在预测损失;设计量化网络与全精度网络对应池化层输出误差为辅助损失项,起正则化作用。

图1 PointNet模型压缩总体流程Fig.1 Overall flowchart of proposed PointNet model compression

问题定义:全精度网络模型用f(x;α)表示,其中x是网络输入,α是全精度模型参数;二值量化网络模型用q(x;β)表示,其中β是量化模型参数。通过知识蒸馏,最小化目标函数,为二值量化网络学习优化的参数β使得q(x;β)接近f(x;α)的性能。学习过程中蒸馏损失函数定义为LKD,其中蒸馏软目标损失项为LDS,预测损失项为LCE(表示量化预测损失项LCES或全精度预测损失项LCET),辅助损失项为Lreg。通过最小化损失函数,使量化模型达到收敛,减少量化模型预测误差。

1.2 蒸馏损失

训练全精度网络学习得到的优化参数为:

(1)

全精度网络输出预测概率为:

(2)

其中:下标f表示全精度网络;T为温度超参数,该参数控制对软目标的依赖程度,随着参数值的增大,软目标的分布更趋均匀。

蒸馏软目标损失为:

log2pq(li=z|xi;β*)]

(3)

其中,Δ表示训练样本序号标识集,Z表示标签集,z为类别标签,下标q表示量化网络,β*为量化网络学习的参数。

一方面,考虑量化预测与全精度预测的差异;另一方面,同时考虑量化预测与真实标签的差异:

(4)

则蒸馏损失为:

LKD=λLDS+(1-λ)LCE

(5)

其中,λ是平衡二者重要性的超参数。

1.3 辅助损失

在分析二值量化网络中最大池化对其性能影响的基础上,提出正则化辅助损失项。

1.3.1 最大池化对性能影响分析

从信息熵[19,36-38]角度考虑,信息熵反映了所含信息量的多少或者复杂程度,经过池化操作后得到的分布的熵越小,特征的可区分性越低,相反熵越大,所含信息越“多样化”,特征可鉴别能力越强。

对全精度进行二值量化,考虑条件熵,即在已知全精度变量F下的二值量化变量Q的不确定性:

(6)

使用量化函数sign进行二值量化,有pQ|F=f(q)={0,1},则下式成立:

(7)

可知二值量化后的熵必然小于全精度的熵,量化必然导致特征表达能力下降,远不如全精度特征表达性能。信息熵的取值范围为[0,log2m],其中m为类别数。对于二值量化而言,m取值为2,熵最大值远小于全精度的最大熵值,决定了其特征表征的能力范围十分有限。

记最大池化操作为φ(·),池化层输入为Iφ,输出为R,经最大池化输出与输入概率质量函数关系为:

(8)

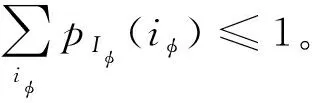
对于二值量化,最大池化后特征熵为:

(9)

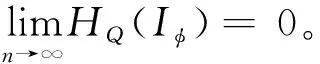
(10)

故当wn=0.5时取最大值,设此时n取值为nopt。当wn<0.5时递增,正如之前分析的,即使增到最大值,二值量化熵值依然较小,特征表征能力很有限;当wn≥0.5时递减,随着n的不断增大,熵值递减直至趋于0,最大池化后的特征表征能力也大幅下降。从二维图像到三维点云,网络池化聚合核的尺寸也急剧增大,导致特征可鉴别能力严重下降。

1.3.2 正则损失项

通过以上分析,为了进一步减小最大池化对二值量化性能的影响,通过让量化网络的池化层输出去学习全精度网络的池化层输出,进而引入误差正则化项来优化目标损失函数,提高量化模型泛化能力。对于隐藏层,仅学习有较大影响的池化层输出知识对计算代价要求较低,是可取的。

辅助损失项定义为:

(11)

其中,g(·)表示正则化函数,h表示池化层输出,下标q和f分别表示量化网络和全精度网络,上标p标识对应的池化层。

这里,g(·)选取常见正则化项[39-40],作为辅助损失项便于对比分析,如表1所示。各范数表达式依据上标区分,如上标F标识取F-范数(通常也称L2范数),其余符号标识类同。

表1 正则化项Tab.1 Regularization terms

1.4 训练策略

1.4.1 训练损失函数

当采用预先训练好的全精度模型作为教师模型时,将第1.2节和1.3节设计的损失函数相加作为二值量化网络蒸馏训练总的损失函数:

Ltotal1=LKD+η·Lreg

=λ·LDS+(1-λ)·LCE+η·Lreg

(12)

其中,η为衡量蒸馏池化层输出特征重要性的超参数。

1.4.2 训练方案

全精度网络模型已预先训练好,网络训练采用离线训练的方式,知识从预训练的全精度模型转移到二值量化模型,具体见算法1。

算法1 离线蒸馏训练Alg.1 Offline training with knowledge distillation

2 实验

实验配置:Intel©CoreTMi5-9400,内存16 GB;显卡NVIDIA GeForce RTX 2080Ti。本文实验采用点云公开数据集ModelNet40,包含40个类别的12 311个三维形状。实验选取4种典型的二值量化算法——BNN、XNOR、IRNET和BiPointnet,算法对比如表2所示。实验中各算法标识含义:BNN+MAX为点云网络量化采用BNN算法、最大池化;BNN+MAX+KDR为在BNN+MAX的基础上进行知识蒸馏和辅助正则化(用KDR标识);BNN+EMA表示点云网络量化采用BNN算法和最大熵聚合(EMA)方法,其中,EMA利用信息熵减少池化特征信息损失;BNN+EMA+KDR表示在BNN+EMA的基础上进行知识蒸馏和辅助正则化;对于其他二值量化算法XNOR、IRNET和BiPointnet,其标识含义类似,其中LSR+EMA即为BiPointnet。本实验所有原算法运行结果与对应改进算法基于相同的实验配置得出。

表2 所选量化算法对比Tab.2 Selected quantization algorithms comparison

2.1 不同参数T的影响

实验主要验证不同T取值对蒸馏结果的影响,其取值为1到10。任选一种正则化项进行验证,本实验选取F-范数,针对8种算法的具体实验结果如图2所示。

图2 不同T值的结果变化曲线Fig.2 Variable curves for various T

综合分析可以看出,随着T值的增大,精度整体呈现下降趋势,较高的精度以大概率集中在[1,3]的T值区间内。当T值取1到10时,8种方法各有10个精度值,有2种算法在T=1时取到各自最大值,4种算法在T=2时取到各自最大值,2种算法在T=3时取到各自最大值,故本实验统一取T值为2。此实验结果符合Hinton在文献[29]中指出的结论,当学生网络比教师网络小得多时取值较小的T比较大的T更有效。而二值量化网络与全精度网络相比,位数极限压缩至1位,与全浮点数的网络相比小很多,因此选取小的T值效果更好,本实验选取T的值为2是合理的。

2.2 不同正则化项的比较

本实验主要对比不同正则化项在不同量化方法中的性能,进而验证后续实验选取何种正则化项。实验选取T=2,针对4种方法BNN、XNOR、IRNET和BiPointnet进行对比实验,其中前三种池化聚合为MAX,最后一种聚合方法采取EMA。为了验证正则化项的有效性,在原损失函数的基础上,设计总损失函数为:

Ltotal=Lorigin+η·Lreg

(13)

实验结果如表3所示,加粗数字分别为同种量化方法不同正则化项中的最高精度。可以看出,1-范数在三种方法中取得了最高精度,且具有明显比较优势,在对BiPointnet正则化后精度甚至高达86.9%,对XNOR正则化后精度也突破86%,在BNN方法中精度55.8%仅次于无穷范数的56.4%。而L1范数性能最差,正则化提升幅度小,甚至存在低于原精度情况,如对BiPointnet正则化精度仅为82.6%,低于原精度3.5%,没有起到正则化作用。从精度来看,1-范数总体上性能优于其他类型。图3为XNOR量化方法添加不同正则化项得到的误差随训练次数变化曲线。可以看出,1-范数正则化方法具有较好的收敛性能,随着训练次数的增加,尤其在训练160次后,相比较于其他范数其误差收敛到最小值,获得最高精度,而L1范数的正则化性能明显低于其他范数。综上分析,后续实验统一选取1-范数作为损失正则化项。

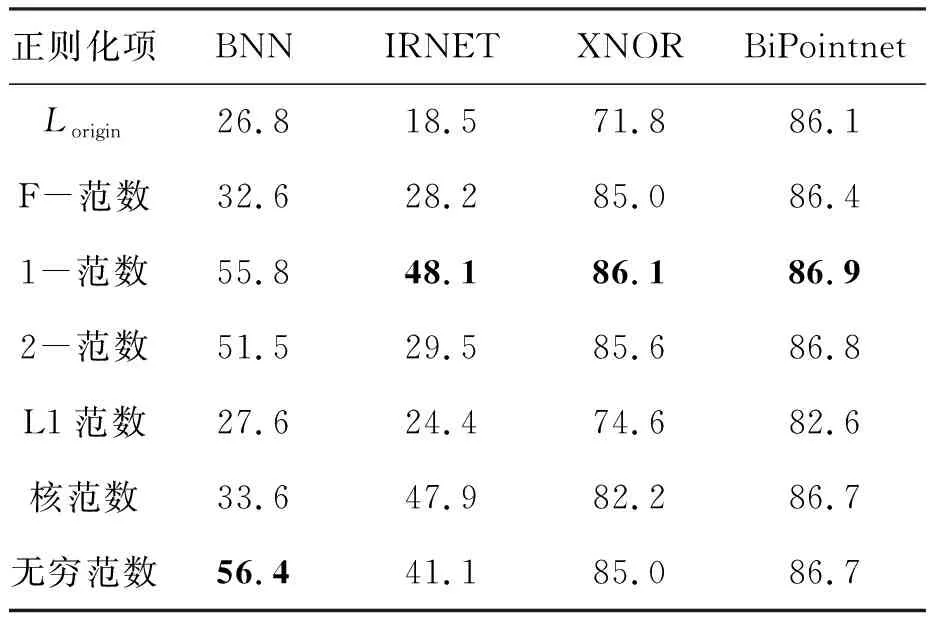
表3 采取不同正则化项的实验结果Tab.3 Experiment results of various regularization terms %

图3 正则化误差变化曲线Fig.3 Regularization error variation curves

2.3 对比实验

本实验依据选取的二值量化算法BNN、XNOR、IRNET和BiPointnet,选取最大池化或改进的最大熵聚合以及是否进行知识蒸馏和正则化,对8种算法的精度进行对比验证,结果如表4所示。可以看出,在选取最大池化而未进行蒸馏正则化的四种算法BNN+MAX、XNOR+MAX、IRNET+MAX和LSR+MAX中,除XNOR外,其他算法精度均大幅小于全精度算法;在进行知识蒸馏和池化正则化后,XNOR算法精度提高了14.6%,其余三种算法精度提升幅度均在双倍以上,由此可以看出加入本文蒸馏正则化后实现了算法性能的大幅提升。采用最大熵聚合的四种方法BNN+EMA、XNOR+EMA、IRNET+EMA和LSR+EMA,加入蒸馏正则化后精度分别提高了35.7%、3.6%、10.4%和1.0%,更接近全精度模型精度,尤其是LSR+EMA+KDR将精度提高到了87.1%。

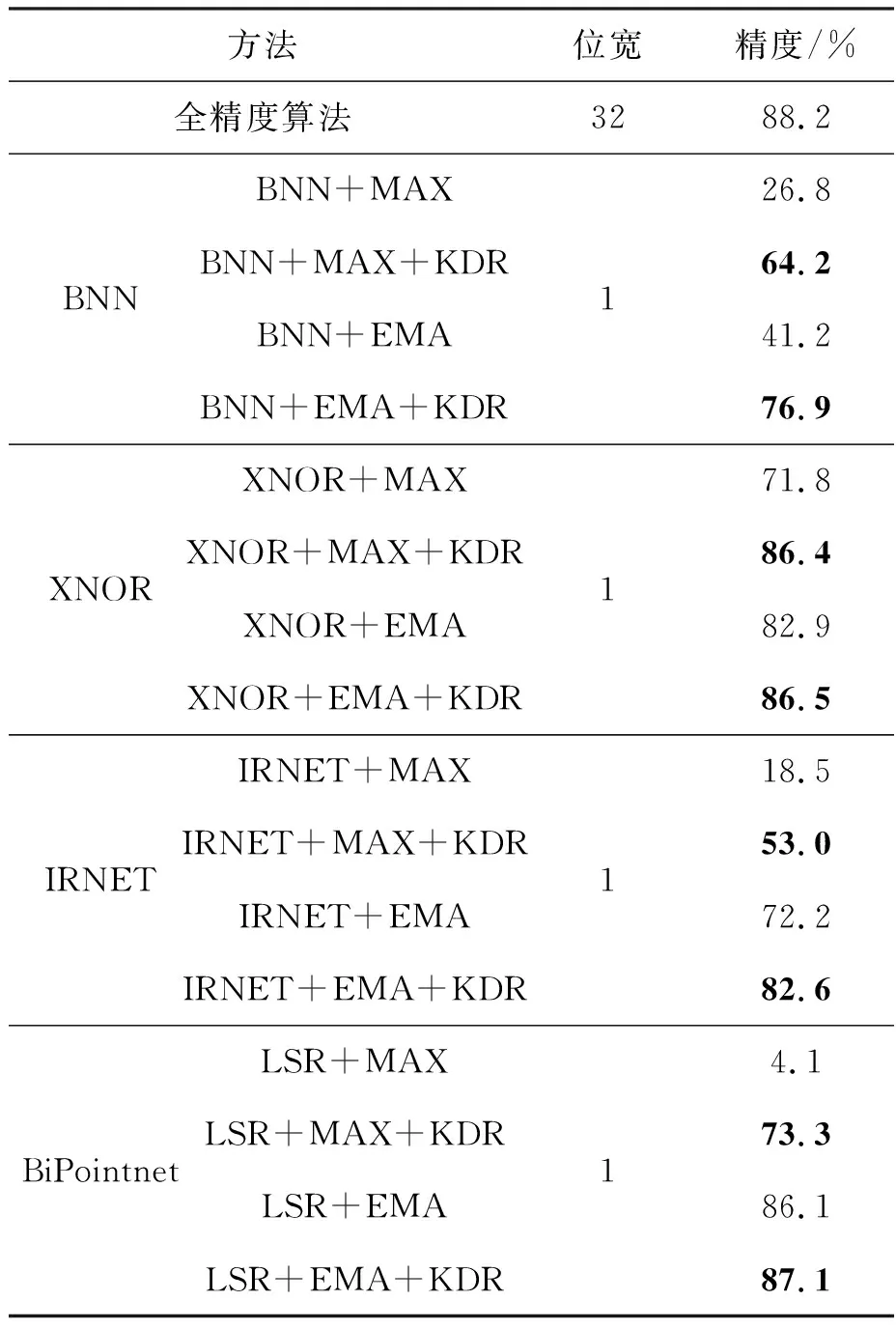
表4 对比实验结果Tab.4 Comparable experiment results

2.4 消融实验

本实验主要验证两个模块包括知识蒸馏和辅助正则化的作用效果,分别用LKD和Lreg标识。实验结果如表5所示,与原算法相比,两个模块单独作用时精度均有提升,两个模块共同作用时的算法精度均高于单个模块作用时的精度。使用最大池化,BNN、IRNET、XNOR和LSR四种算法单模块作用时精度均大幅提升,知识蒸馏单独作用时精度分别提升了16.9%、16.8%、12.5%和45.8%,而在正则化单独作用时精度分别提升了29.0%、29.6%、14.3%和50.3%。使用最大熵聚合,四种算法单模块作用时精度也有不同程度的提升;BNN算法提升幅度最大,其中知识蒸馏单独作用时精度提升了34.3%,在正则化单独作用时精度提升了33.9%。综上可以看出,知识蒸馏和正则化对量化模型精度的提升作用非常明显。

表5 消融实验结果Tab.5 Ablation experiment results %

2.5 拓展实验

本实验旨在验证本文所提算法的泛化性能。在PointNet模型实验基础上,选取另外典型的3种点云主流骨干网络模型PointNet++、PointCNN和DGCNN,选用XNOR和BiPointnet两种二值量化方法,所得实验结果如表6所示。经分析得出,相比于XNOR+MAX和LSR+EMA(由于PointCNN采用X-Conv取代最大池化,因此本实验中未添加池化正则化损失项,采取XNOR+KD和LSR+KD),各网络的精度均有提升,验证了算法的泛化性能。图4给出DGCNN在全精度、LSR+EMA和LSR+EMA+KDR三种算法下测试误差随训练次数变化的曲线,本文算法误差曲线整体上介于全精度和LSR+EMA误差曲线之间,说明基于知识蒸馏和辅助损失的方法改善了DGCNN量化精度性能,更接近于全精度网络精度。

表6 拓展实验结果Tab.6 Extended experiment results

图4 误差随训练次数变化曲线Fig.4 Variable error curves with training numbers

2.6 复杂度分析

本实验通过时间复杂度浮点运算次数(floating point operations,FLOPs)和空间复杂度参数量两个指标来衡量点云深度模型量化压缩后的性能。本节主要分析采用所提8种量化方法对PointNet模型量化后的性能,在其余主流点云深度模型中的量化性能分析与此类似。表7给出了PointNet及其各种量化方法的表现性能,包括单样本浮点运算数(FLOPs/sample)、加速比、参数量和压缩比四项。

表7 复杂度分析结果Tab.7 Complexity analysis results

由表7可以分析得出,相比于全精度模型,8种方法平均加速45倍,其中BNN+MAX+KDR、IRNET+MAX+KDR和LSR+MAX+KDR这3种方法加速50倍以上,而加速比最小的XNOR+EMA+KDR也加速了37倍。相比于全精度模型参数量,除XNOR+MAX+KDR和XNOR+EMA+KDR外,其余6种方法参数量压缩均在22倍以上。由于XNOR量化是对各通道进行量化,因而相比于其他方法,参数量要大,精度也相对高于BNN和IRNET。相比较而言,LSR+MAX+KDR和LSR+EMA+KDR分别在最大池化(MAX)和最大熵聚合(EMA)的同类方法中性能最优,保持高精度的同时具有高加速比和高压缩比。综上分析,本文所提点云深度模型加入知识蒸馏和正则化后,大幅度提高精度的同时,具备了较高的加速和压缩性能。

3 结论

针对三维点云深度学习网络模型存在的应用实际问题,结合当前二值量化模型研究现状,将知识蒸馏方法引入点云二值量化模型中,解决了量化精度大幅下降问题。同时考虑相比于二维图像,三维点云深度学习模型有其特殊性,本文在分析池化聚合影响的基础上,提出了正则化辅助损失函数项,与蒸馏损失项共同构成总的损失函数,有效地解决池化对点云二值量化模型预测精度的不利影响。通过在公共数据集上实验,结果显示,该算法可以使点云二值量化模型取得更接近全精度模型精度的性能,同时取得较高的加速比和压缩比,而且可以较方便地移植到其他主流点云深度学习网络模型上。