GNSS/INS超紧组合导航综述*

倪少杰,李诗扬,谢郁辰,邓 丁

(国防科技大学 电子科学学院, 湖南 长沙 410073)

全球导航卫星系统(global navigation satellite system,GNSS)经过数十年研究发展,已经能够实现全天候的室外高精度定位。但GNSS定位原理决定了接收机需要至少4颗卫星的信号才能解算出位置信息,且卫星信号较弱,易受电磁干扰与遮挡。而惯性导航系统(inertial navigation system, INS)具有不受环境约束的特性,能够实现完全自主定位,但其缺陷在于漂移误差会随着工作时间推移而不断累积。因此,在卫星信号较弱的多遮蔽环境下将GNSS与INS进行组合实现优势互补成为导航定位领域的热点方向。

GNSS与INS的组合导航方式一般可分为松组合、紧组合和超紧组合三种[1-2],其中,松、紧组合本质上都是使用GNSS辅助INS进行导航,在卫星信号失锁时,INS仍然会出现误差累积。超紧组合在紧组合基础上使得组合滤波器也向接收机反馈校正信息[1],能够实现更深层次的组合,大幅提升了鲁棒性。因此,本文对于超紧组合系统结构特点、发展现状进行分析,对超紧组合涉及的关键技术及发展前景进行总结和展望。

1 组合导航系统基本原理

1.1 GNSS定位原理

GNSS主要由卫星星座、地面站和用户设备组成[3]。码伪距绝对定位是最常用的定位方式之一,其原理可以简述为:首先由某颗卫星下行发送测距信号和导航电文;用户接收机接收到测距信号后可以解算出自身与该卫星间的伪距,形成一个伪距观测方程,并从星历中解算出卫星位置、钟差等信息;GNSS需要至少4颗卫星才能完成位置解算,这些卫星形成的伪距方程构成方程组,对其进行解算即可获得用户在某一坐标系下的位置。

1.2 INS定位原理

INS是一种航位推测(dead reckoning, DR)系统[4],其以牛顿力学定律作为理论基础,通过某一已知位置结合加速度、角度等位姿信息推算下一时刻位置。INS常用器件主要有加速度计、陀螺仪等,陀螺仪输出信息用于确定载体姿态,加速度计输出用于解算运动物体当前位置。受到惯性器件精度限制,INS存在随时间累积的漂移误差。高精度惯性测量单元(inertial measurement unit, IMU)可以有效改善累积误差,但其高昂的成本以及体积、功耗上的要求对其广泛应用造成极大限制[5]。

1.3 松、紧组合导航系统原理

GNSS与INS的互补特性从各自的定位原理中初现端倪。在卫星信号衰弱的环境下INS可以不受影响地持续进行导航作业;而INS随时间累积的误差可由GNSS进行校正。

INS与GNSS作为子系统相对独立的组合方式称为松组合,这是最易实现的组合方式[6]。松组合系统将INS、GNSS子系统各自对速度、位置信息的估计结果通过卡尔曼滤波器进行融合,由于GNSS内部滤波过程未知,其组合滤波本质上成为级联滤波。在GNSS信号弱或卫星不可见时,松组合系统会直接输出INS定位信息,因此松组合又被称为GNSS辅助INS的组合方式。松组合的系统结构如图1所示。

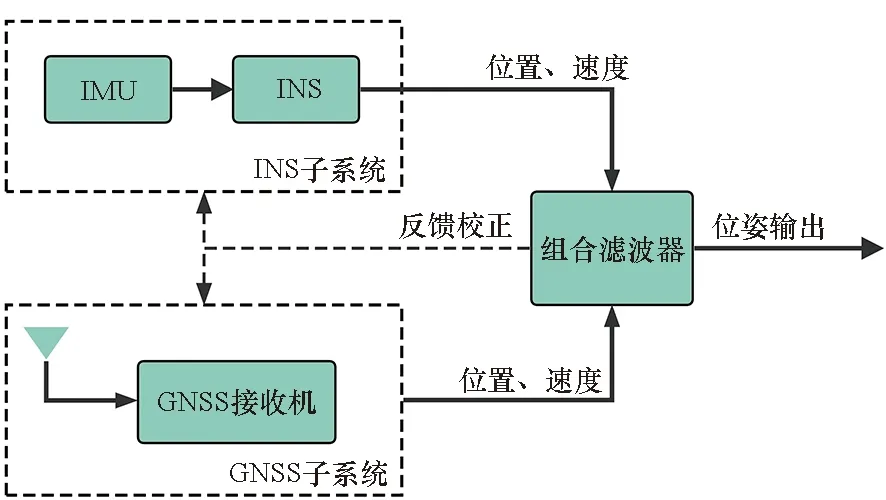
图1 松组合系统结构Fig.1 Loose integration system architecture

紧组合指GNSS与INS在伪距、伪距率[6]、载波相位[7]等领域进行信息融合的组合方式。在紧组合系统中,GNSS和INS不再作为独立的子系统直接提供位置和速度信息,而是作为不同传感器提供伪距、伪距率等量测信息,并将状态量构建于同一个状态方程当中。紧组合系统的状态方程分为INS的误差状态和GNSS的误差状态两部分,INS对位置的估计被用来辅助GNSS进行模糊度固定,并通过组合滤波结果对INS的误差进行校正,从而实现精度的提升[8-9]。即使卫星数目不足,紧组合系统仍能利用GNSS观测进行组合滤波。一种典型的紧组合系统结构如图2所示。

图2 紧组合系统结构Fig.2 Tight integration system architecture

松、紧组合的相同之处在于都是利用GNSS信息辅助INS,其本质区别在于INS是否向GNSS反馈先验位置信息[10]。相较于松组合系统而言,紧组合系统算法实现更为复杂,但整体性能有大幅提升,尤其在可见卫星数量小于4颗时,对卫星的观测信息仍然可以用来对INS的误差进行修正[11]。尽管如此,松、紧组合的缺陷仍然显而易见:长时间作业时导航精度依赖于接收机,当接收机受到多径干扰或处于信号微弱环境下时,输出的导航解极易受到影响。

2 超紧组合导航系统的演变与结构

2.1 发展沿革与概念分歧

美国国防部于20世纪80年代正式启动全球定位系统(global positioning system, GPS)计划,而在GPS计划初期,采用INS量测信息辅助GPS环路跟踪的组合导航思想就已经初见雏形。同一时期,Cox[8]首次对使用INS辅助GPS信号的捕获、跟踪环节的方法进行了详细阐述。1996年,美国Draper实验室的Gustafson首次使用深组合的概念来描述一种扩展码跟踪环路的组合导航方式,Draper实验室在与军方合作的武器装备制导项目中已经对超紧组合做了深入研究并推动其落地[12]。在这一时期,超紧组合/深组合的理论基础逐渐形成,其特点是用INS信息辅助GNSS接收机的标量跟踪环路。

1996年,Spilker等[13]首次提出矢量跟踪环路的概念。不同于标量跟踪环路使用各个独立通路获取伪码相位误差和载波频率误差,矢量跟踪环路将所有通路的信息集合为一个观测矢量进行参数估计,获得了更好的灵敏度和抗干扰性能[14]。矢量跟踪环路的经典结构如图3所示,它的提出为超紧组合概念的形成奠定了基础。1999年,Aerospace公司提出一种基于级联卡尔曼滤波器的惯性辅助矢量跟踪环路的组合导航系统,并正式将其命名为超紧组合[15]。

图3 矢量跟踪环路结构图Fig.3 Structure diagram of vector tracking loop

在矢量跟踪技术出现之后,相关领域研究者们分别对基于矢量跟踪和基于标量跟踪的超紧组合系统展开研究,并在深组合与超紧组合的定义上产生了分歧。对于深组合的定义问题,以斯坦福大学Gautier为代表的研究者认为深组合指利用INS辅助GNSS接收机跟踪环路的方法[16];而Gustafson等认为只有利用INS辅助矢量跟踪环路的方式才能称为深组合[17]。

而业界对于超紧组合的概念也没有明确的界定。相较于松、紧组合而言,超紧组合和深组合从广义上均表示利用INS辅助GNSS跟踪环路的方法;主流观点一般认为深组合与超紧组合概念相同[3,18-22],指用INS信息辅助矢量跟踪环路。以武汉大学牛小骥团队[23-24]为代表的一部分研究者认为深组合系统根据其接收机跟踪环路的不同可划分为标量深组合和矢量深组合两类,而超紧组合与其中的矢量深组合概念是等同的,即超紧组合必须依赖矢量跟踪环路。图4展示了业界对超紧组合概念存在的分歧。

图4 超紧组合概念分歧Fig.4 Divergence on the concept of ultra-tight integration

2.2 系统分类与结构特点

鉴于标量深组合系统并未实现各通道完全信息共享,且考虑到超紧组合概念上的争议,重点关注基于矢量跟踪环路的超紧组合系统。超紧组合系统的结构如图5所示。

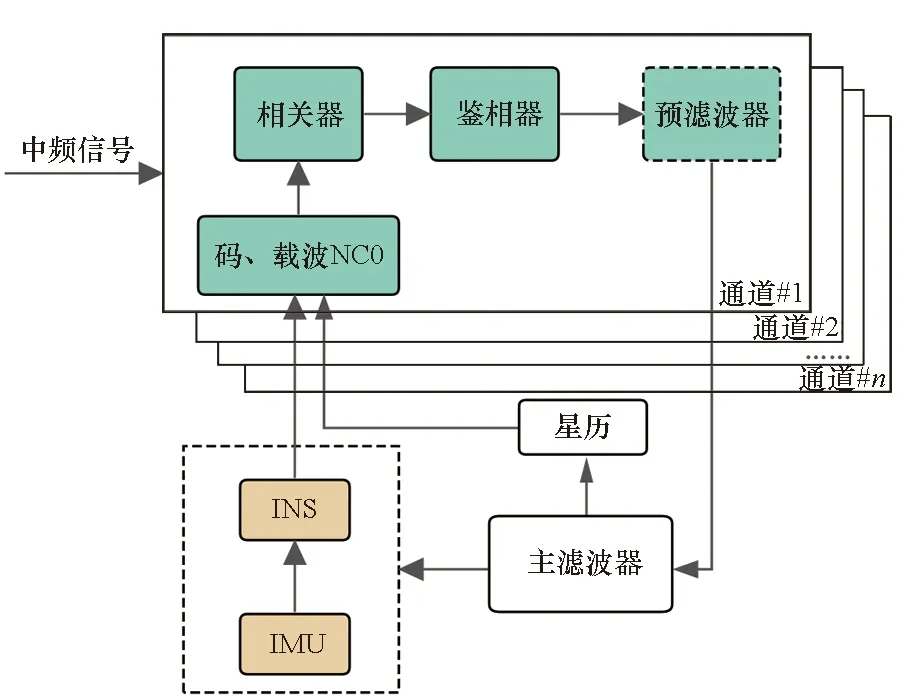
图5 超紧组合系统结构Fig.5 Ultra-tight integration system architecture

不同于传统的标量跟踪环路将不同卫星的信号分配到相互独立的信道中处理,矢量跟踪环路融合了跟踪不同卫星的通道信息,用强信号辅助弱信号的跟踪,可以同时产生伪距、伪距率信息[14]。矢量跟踪环路将所有通道的码相位误差和载波频率误差汇集到一个卡尔曼滤波器中进行滤波,相较于标量跟踪环路而言工程实现更为复杂,精度也更高。矢量跟踪的优势在于其在弱信噪比环境下性能更好,在卫星信号丢失后仍能进行一段时间的跟踪,并在信号重新出现时快速进行重捕,在信号衰减15 dB时仍然能够跟踪载波相位[20]。此外,矢量跟踪环路也在接收机高动态环境下表现出更好的性能[25]。

超紧组合系统的分类方式众说纷纭。例如,其中一种分类方式[26]根据伪距残差获取方式的不同和用于做差的数据不同将超紧组合系统分为基于相关数据浅度融合、基于相关数据深度融合和伪距数据融合超紧组合三种类型。但通常而言基于矢量跟踪的超紧组合依据结构上的区别主要可以分为集中式和级联式两种。

集中式超紧组合最早由Spilker等[13]提出,其特点是采用一个组合滤波器负责处理所有通道的跟踪信息以及数据融合信息,其输出结果会对INS的累积误差进行校正,同时参与多普勒估计以辅助载波跟踪过程。

级联式超紧组合起源于Abbott等设计的采用预滤波器的结构[15]。级联式系统因其采用两级滤波器的架构而得名,基带I/Q信息首先通过各通道的预滤波器进行处理,这些预滤波器的输出再作为主滤波器的量测。预滤波器的功能是对GNSS原始数据进行处理,并估计主滤波器码相位、载波频率预测值的误差,周期性地校正主滤波器[27]。

相关器输出的I/Q信号被作为组合滤波器的测量值;组合滤波器的输出一方面对INS进行校正,另一方面通过计算星历并和INS的输出一起调整数控振荡器(numerically controlled oscillator, NCO)与载波NCO[26];INS通过测量矢量跟踪环路滤波器每次更新周期之间速度和位置变化并反馈给跟踪环路以提高接收机高动态性能[20]。

集中式与级联式超紧组合均直接通过各通道I/Q值作为滤波器量测,因此都属于相干超紧组合。表1对不同类型的超紧组合实现方式进行了对比与总结。

表1 不同超紧组合实现方式对比Tab.1 Comparison of different kind of ultra-tight integration

3 超紧组合系统研究进展

自1999年超紧组合概念提出以来,国外研究者首先进行了原理发展和工程实现,而近年来国内研究人员对超紧组合理论进行深入研究和完善,研究深度从仿真到工程实现再到商用产品,研究广度覆盖跟踪环路优化与跟踪算法设计、故障检测与控制、低成本微机电系统(micro electro mechanical system, MEMS)/GNSS超紧组合等。总体而言,超紧组合技术向着低成本、高精度、强稳定性的趋势发展。

3.1 国内外研究进展

进入21世纪以来,世界各国对超紧组合的研究呈现百家争鸣的态势。澳大利亚新南威尔士大学在超紧组合的研究上起步较早,也取得了显著的成果。Crane[28]在预滤波器部分采用扩展卡尔曼滤波算法以处理其非线性问题;Babu等[29]对超紧组合相较于松、紧组合的优势及系统性能进行了测试评估,关注非线性问题的处理及“城市峡谷”效应的解决[30]。

加拿大卡尔加里大学PLAN实验室深耕于组合导航领域多年,对级联式超紧组合系统有深厚的研究积累,并搭建起实体系统。Petovello等[31]基于级联式系统设计了一种IMU模型,使得超紧组合接收机灵敏度相对于常规接收机提高约5 dB。Gao[32]在其博士论文中采用INS辅助相位锁定环路,实现了在短暂失锁后的快速重捕;Daneshmand等[33]利用超紧组合系统和相位阵列天线进行组合以解决城市森林中多径效应严重的问题。

近年来国外对超紧组合的理论研究热度逐渐消退,现有的研究方向主要集中于对接收机精度与鲁棒性的改进和处理[18],以及结合特定应用场景如城市森林进行研究。

国内对超紧组合导航系统的研究始于20世纪80年代末,以高校为主的一批研究机构才逐步开始进行研究[34-35],研究方向主要瞄准麻省理工学院Draper实验室提出的集中式超紧组合结构。直到2010年,对超紧组合研究的热度才开始逐渐上升[23]。对超紧组合理论研究做出主要贡献的几所高校主要有西北工业大学、国防科技大学、北京航空航天大学、武汉大学等。

西北工业大学是国内最早研究超紧组合技术的机构之一。1989年秦永元等[34-35]就开始了对INS辅助码跟踪环的研究。近年来仍然热度不减,主要关注故障检测[36]及采用MEMS的超紧组合系统研究[37]。国防科技大学郭瑶等[38]基于无迹卡尔曼滤波(unscented Kalman filter, UKF)算法进行了超紧组合算法的车载实验,设计了微型惯性测量单元(miniature inertial measurement unit, MIMU)辅助GNSS跟踪环路的结构;何晓峰研究了基于软件接收机的BD-2/MIMU深组合算法[39],其他研究人员在基带滤波器设计[38]、误差抑制[40]、跟踪算法设计[41]等方面也取得了大量成果。北京航空航天大学研究方向广泛,对MEMS-捷联惯性导航(strapdown inertial navigation system, SINS)超紧组合系统的跟踪环路改进[42]、抗干扰[43]、高动态情况[44]等细分领域均有所涉猎。

武汉大学研究人员针对级联型超紧组合结构做了大量研究工作,其研究主要基于标量深组合结构。研究团队搭建了工程样机,验证了超紧组合系统在挑战性环境下的性能[45-46],并对级联型超紧组合结构做了改进,验证了其相较于传统级联型系统的性能提升[45-46]。此外,武汉大学团队对于超紧组合系统在高动态、低成本[22]以及与北斗导航系统结合[47]等方面的研究均作出了贡献,其对超紧组合概念及分类上的理解自成体系[23]。

目前国内对超紧组合的研究日益深入,逐渐从实验室走向实际应用。2020年,ADI与北云科技合作推出的A1高精度组合导航板卡即内置了深耦合算法;2022年北云推出的新型专用集成电路(application specific integrated circuit, ASIC)芯片Alita内置的超紧组合算法能够达到失锁重捕时间小于等于1 s、跟踪灵敏度达到-145 dBm;千寻位置基于Alita芯片设计的组合导航板卡可以实现厘米级定位;北斗星通的产品SPAN-μIMU-IC采用NovAtel SPAN深耦合技术,实时动态 (real-time kinematic,RTK)定位精度可以达到1 cm,在卫星信号中断60 s后仍能维持在15 cm。表2展示了国内外部分公司具有代表性的商用深耦合导航产品性能对比。

3.2 高动态下超紧组合系统研究进展

美国喷气动力实验室(jet propulsion laboratory, JPL)对高动态场景的定义是载体承受50g加速度、100g/s的加加速度。高动态下跟踪误差主要来源于载体与卫星相对运动带来的动态应力噪声,这直接决定了跟踪环路能否正常工作[12]。松、紧组合结构没有将载体动态信息反馈给跟踪环路,在载体受动态应力误差较大的情况下极易出现失锁,而超紧组合结构因其采用INS信息辅助GNSS信号跟踪环路的做法可以在高动态环境下极大提升载体的动态跟踪能力[48]。

目前国内外对高动态下超紧组合系统进行了大量研究,已有多个工程样机得以实现。美国Rockwell Collins公司研制的NavFire系列超紧组合系统面向武器装备应用场景进行设计,可以承受25 000g的冲击,且系统高度集成,重量仅为19g。武汉大学[24]搭建的标量深组合导航系统能够在30g/s的加加速度下实现实时解算(如图6所示)。Langer等[49]实现了高动态下多星座超紧组合原理样机,并能在本地计算机上进行实时解算。

图6 武汉大学研制的深组合样机[23]Fig.6 Deep combination prototype developed by Wuhan University[23]

在接收机高动态情况下,载波相位测量通常比较脆弱,模糊度难以确定,此时超紧组合系统往往表现出极大的非线性[50]。处理非线性问题的常用滤波方法有扩展卡尔曼滤波(extended Kalman filter, EKF)算法、UKF算法、粒子滤波(particle filter, PF)算法等。Jwo和丰泽斌等分别对于这三种滤波算法在超紧组合系统中的性能进行了仿真分析,认为PF算法在位置、速度、姿态三个方面的精度都优于其他两种算法,且收敛速度也最快[21,50]。

基于此对比,文献[1]提出了一种利用交互式多模型(interactive multi-tude model, IMM)算法跟踪变噪声的改进UPF算法,相较于UPF算法,在经纬度估计误差、天北向速度估计误差方面均至少降低40%;文献[50]提出了一种通过改进固定矩阵平方根以高效获取Sigma点的改进UKF算法,其均方根误差相较于传统UKF算法至少降低70%,且运算复杂度更低;文献[21]提出一种模糊逻辑自适应系统(fuzzy logic adaptive system, FLAS)辅助UPF的方法,通过检测发散度的增加自适应地增加比例因子从而保持良好的跟踪能力。

除上述三种滤波算法之外,容积卡尔曼滤波(cubature Kalman filter, CKF)算法日益受到关注。相较于EKF算法,CKF算法减小了高维滤波时产生的误差;同时避免了UKF算法在实际应用中难以选择合适参数、计算复杂度随采样点数快速增加的问题。文献[51]提出了一种基于CKF算法的超紧组合滤波算法,验证了CKF算法相较于EKF算法和UKF算法精度均有提升。文献[52]针对MEMS/GPS/极化罗盘的组合导航系统提出一种多采样率强跟踪的CKF算法。文献[22]通过修改NCO将辅助多普勒信息插值到局部信号的样本中,进一步消除了动态误差。面向机载、弹载等算力受限情况下的超紧组合结构中CKF算法是一个更富前景的研究方向。表3对EKF算法、UKF算法以及CKF算法三种非线性滤波算法特点进行了总结。

表3 三种非线性滤波算法对比Tab.3 Comparison of three nonlinear filtering algorithms

3.3 MIMU/GNSS超紧组合系统研究进展

MIMU是MEMS的一种,由微型陀螺仪、微型加速度计、专用集成电路及嵌入式微机组成。MIMU具有成本低、体积小、功耗低的优势,已广泛应用于超紧组合系统当中[53-54]。然而低成本往往意味着更高的误差和更强的不稳定性。当采用MIMU时,组合导航精度不足以对GNSS载波相位进行精确估计。对于NCO不完全由导航信息控制的超紧组合系统,如矢量延迟频率锁定环(vector delay frequency lock loop, VDFLL)而言,MIMU对跟踪环路的辅助误差将不再等于信号跟踪误差。因此研究人员针对MIMU引入的误差校正与控制问题进行了大量研究。

21世纪初,Draper实验室在军用领域的MEMS/GNSS研究上已经取得了一定的成果,其于2003年资助的Low-Cost INS/GPS计划已经实现MIMU与GPS的芯片级超紧组合,并运用于军用领域[55]。国内超紧组合系统的商品化尚且处于起步阶段,对于MIMU/GNSS超紧组合的研究主要侧重于器件误差补偿以及MIMU辅助接收机捕获和跟踪环路,相关技术集中于实验室研究,尚无成熟的商用产品出现。

使用低精度MEMS会使得多普勒辅助误差迅速增加。针对这一问题,文献[42]采用时间差分载波相位速度辅助跟踪环路,减少了载波环路噪声带宽和码相关器间距,进而提高跟踪精度。而文献[56]在文献[42]的基础上采用时空差分载波相位速度辅助载波环路,减少了由低精度MEMS引起的多普勒辅助误差。文献[57]通过引入双天线载波相位差分提升了MIMU/GNSS的航向精度,并且直接将载波相位差作为量测量,可以根据MIMU对姿态的预测检验当前相位差测量值是否存在周跳并及时校正。

接收机高动态情况下,MIMU的比力测量误差会导致较大的频率跟踪误差跳变,这会导致导航解的较大误差甚至失锁。文献[58]提出了一种增强型MIMU/GNSS超紧组合结构,在传统级联型超紧组合结构的基础上在每个通道增加了大幅频率误差检测器和串行精细频率处理器,并使用带有多衰落因子的自适应预滤波器代替传统的预滤波器,实现载噪比几乎不受较大频率误差的影响,最大速度误差也不超过2 m/s。叶萍[5]定量评估了接收机在有无MIMU辅助状态下的捕获性能区别,设计了一种高动态情况下MIMU辅助接收机跟踪环路的方法,结果证明在加加速度为10g/s的高动态情况下能够实现三阶锁相环带宽门限降低到1 Hz,接收机整体抗干扰性能提升7.4 dB。

超紧组合系统的高精度与强稳定性无可避免地带来了计算复杂度与功耗的提升,而计算负载与功耗直接与GNSS信号的相关性和接收器的激活时间成正比[59]。针对小型GNSS设备计算能力与续航时间的限制,文献[60]提出一种在维持导航精度的情况下对GNSS进行间断跟踪的方法进行高效计算,并通过车载实验证明其有效性;在此基础上又提出应用不同的间隔跟踪不同波长的GNSS码信号[59],通过非相干码鉴别器代替跟踪环路来获取码相位跟踪误差的方式降低计算需求。文献[61]同样试图通过非连续跟踪降低计算量,其实验证实在相干积分时间为1 ms时,跟踪间隔为10 s的非连续跟踪相对于连续跟踪的相干积分计算次数减少了4个数量级。为了减少相关性计算带来的资源消耗,文献[62]采用多相关器值作为充分统计量,实现了无损的样本信息压缩。Luo等[63-64]验证了智能手机中的消费级IMU是否足以支持GNSS接收机的基带,并在实车测试中使用U-Blox接收机验证了采用消费级IMU的超紧组合系统可用性达到99.3%[64]。

综上,随着误差补偿以及功耗控制技术的发展,未来GNSS/MIMU超紧组合系统将凭借其成本低、体积小等优势在军用、民用等领域得到广泛应用,其重要发展方向之一就是实现芯片级集成。

4 超紧组合系统关键技术

对超紧组合系统的研究日益深入,但仍有许多关键技术没有得到突破,现有的研究成果不能满足实际应用需要或不成体系,亟待研究人员持续推进研究。

4.1 容错控制技术

矢量跟踪环路的一个重要特征是通道之间的相互辅助,这种结构可以有效提升系统在低信噪比情况下的性能。但当某颗卫星出现异常时,其对应通道的故障信息也会在其他通道间进行传播,并且难以锁定实际出现故障的通道。随着误差不断相互传播和积累,接收机最终会失去对所有卫星的锁定。因此在使用矢量跟踪环路的超紧组合系统中进行容错控制,提升系统安全性、稳定性是一个重要的课题。

对于基于标量跟踪环路的松、紧组合导航系统以及标量深组合系统而言,常用的故障检测方法有卡方检验、小波变换、模糊推理等,然而此类传统方法对通道信息相互融合的矢量跟踪环路难以适用,能够针对超紧组合系统进行故障识别与隔离的方法仍有待研究。目前这一领域出现了一些尝试,但仍缺乏高效精准的检验方法。一些研究人员尝试为每个通道设计子滤波器用以实时监控通道的运行状态,并在子滤波器中采用基于支持向量机的故障检测方法[65]。陈驵针对多通道故障问题提出一种基于子集检验的故障检测算法,并通过仿真验证了其正确性[12]。超紧组合系统容错控制技术的一个新兴方向是结合神经网络进行故障识别。文献[66]提出的利用卷积神经网络(convolutional neural networks,CNN)辅助的鲁棒算法通过维持正确的导航解来降低故障信息对导航解的干扰,通过实车测试证明故障识别的准确率提升超过20%。

4.2 神经网络辅助超紧组合

随着算力的大幅提升与计算机技术的发展,神经网络技术得到了前沿领域的重点关注。同样,神经网络在组合导航信息融合部分也可以发挥其特有的效用。神经网络的最大特点是能实现自我学习,常被用来解决非线性问题或无初值问题。而传统超紧组合信息融合算法使用的卡尔曼滤波器精度取决于对误差模型的建立,如果误差模型不够精确,则卡尔曼滤波会出现较大的发散。因此,神经网络可以用来辅助进行信息融合,其基本方法为:在GNSS正常工作时用INS的加速度计、陀螺仪输出信息对INS误差进行训练,而在GNSS失锁后用训练得到的误差模型对INS的输出误差进行校正。

Noureldin是最早将神经网络方法引入INS误差处理的学者之一,他采用的方法主要依据小波多分辨分析和径向基神经网络[67](radial basis function-artificial neural network, RBF-ANN),而Jwo等[68]将RBF-ANN引入超紧组合系统并结合模糊推理算法提升GNSS失锁后INS的误差预测精度;西北工业大学研究者采用CNN处理基于矢量跟踪环路的超紧组合系统中误差传播的问题[66]。哈尔滨工业大学研究人员提出一种CNN-长短期记忆(long short-term memory, LSTM)网络模型[69],用于改善传统的LSTM网络在处理具有强相关性的导航数据时的性能,速度估计的均方根误差能够降低20%以上。目前面向组合导航的神经网络辅助方法已经有了一些成果,但针对超紧组合结构的方法仍有待研究,现有的一些文章主要通过仿真验证[70],仍缺乏工程样机的实现。

4.3 其他传感器辅助超紧组合

采用其他传感器对超紧组合进行辅助可以解决传统超紧组合方案在高动态情况下以及采用低成本MEMS时出现的性能退化[71]。

视觉传感器辅助GNSS/INS组合导航系统的方案已有不少研究成果,而随着超紧组合系统在复杂环境下的崭露头角,研究人员开始探索视觉辅助超紧组合系统的方案。视觉传感器具有信息误差不随时间累积的特点,其捕获的场景特征也不易受到人为干扰。Cristodaro等[71]使用单目相机辅助传统的超紧组合系统应对高动态、强干扰和采用MEMS传感器时导致的性能退化问题,实车测试证明了视觉辅助的超紧组合系统在注入干扰达到30 dB时仍然能够稳定维持导航功能[72]。文献[73]使用双目视觉辅助MEMS-SINS/GNSS超紧组合系统,使得低空飞行器在强噪声下的位置误差能够保持在5 m以内;文献[74]同样使用双目相机的姿态信息辅助GNSS/IMU超紧组合系统,在GNSS信号中断100 s情况下相较于传统GNSS/IMU超紧组合系统北向速度误差从4 m/s缩减到1 m/s以内,其系统结构如图7所示。

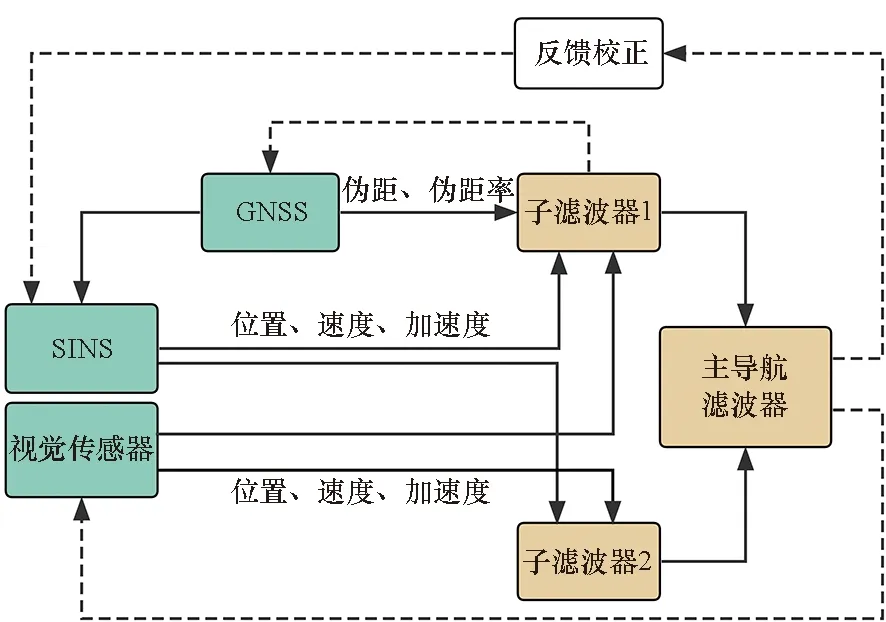
图7 一种视觉辅助超紧组合结构[74]Fig.7 A visually assisted ultra-tight integration architecture[74]

同样,里程计、激光雷达等传感器也可以对超紧组合系统产生辅助效果,不过目前缺乏研究成果,需要研究人员的不断推进。

5 总结与展望

本文对于GNSS/INS超紧组合的基本定位原理、架构特点做了简要介绍,对超紧组合概念的确立过程进行了回溯,分析了超紧组合技术相较于松组合、紧组合技术的优势;介绍了国内外主要研究机构及研究现状;介绍了在高动态下及采用MIMU的超紧组合系统研究进展;总结了仍有待发展的容错控制技术、神经网络辅助及采用其他传感器辅助超紧组合系统等关键技术。

高精度、低成本、强稳定性的导航作业已日益成为人类登天探海的必然要求。导航系统既在军事领域助力统揽全局排兵布阵,又在民用领域下沉到日常生活中。从精度提升角度而言,超紧组合仍需在系统结构上进一步改进,从接收机内部电路出发提升其性能,并与多种导航方式进行组合;从成本控制方面来说,超紧组合研究需要在采用低成本器件的同时改进其误差检测与校正能力,针对小型化设备降低计算复杂度与功耗;从稳定性角度来说,为了应用于高动态、强干扰和弱信号等复杂条件,超紧组合既要提升对非线性状态的处理能力,也要改进失锁重捕技术,并针对不同的干扰手段进行抗干扰技术研究,此外,与其他传感器的结合也是极具前景的研究方向。