采用重构吸引子的辐射源个体识别技术*

赵雨睿,宋川江,王 翔,黄知涛,2

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 电子对抗学院, 安徽 合肥 230037)

特定辐射源个体识别(specific emitter identification, SEI)技术是指仅利用接收的电磁信号的外部特征对辐射源个体身份进行识别的技术。辐射源个体之间的信号外部特征差异来自电子系统器件的非理想性。受到生产工艺的限制,辐射源系统中的功率放大器、本振频率源等器件无法做到完全一致。即便是同一厂家、同一批次生产的同一型号的辐射源,其所产生的信号间也会存在细微的差异[1]。这一差异也被称为辐射源的“指纹”特征,具有不能消除、难以模仿等特点。SEI技术现已被广泛应用于频谱监测、无线网络安全、电子对抗等军民领域[1]。

现有的SEI方法大体一般分为三步,即预处理、指纹特征提取、分类识别[2]。其中,指纹特征提取主要通过对预处理后的数据进行分析和变换,寻找最能反映辐射源个体的特征,是SEI的核心步骤。根据所依据的理论基础不同,指纹特征提取步骤主要可以分为两类:一是基于不同变换域局部特征提取的技术,二是基于非线性动力学理论的整体特征建模技术。

第一类技术的目标是将信号映射至某一特定的变换域内,进而在该变换域中计算不同度量的指纹特征。典型的变换域包含频谱[3-4]、时频图[5-6]、双谱图[7-8]、星座图[9]等。然而基于变换域所提取的指纹特征仅表征辐射源信号某一域内的局部特性,导致特征存在一定的“片面性”。这种“片面性”制约着辐射源个体识别方法对不同信号的适用性以及对不同场景的鲁棒性。

第二类技术是从非线性动力学[10]的角度对辐射源系统进行整体建模,从而识别不同辐射源个体的系统特性。接收机采集到的信号可以看作是发射该信号的辐射源系统在一维空间的映射。根据非线性动力学理论[10],信号一维时间序列蕴含原系统的非线性动力学特性,因此可以作为特定辐射源个体识别的依据。为深入刻画辐射源个体的差异,部分学者利用相空间分析对辐射源非线性动力学系统进行建模与辨识。美国海军实验室Carroll[11]利用相轨迹的微分统计量对不同的功放模型进行识别,证明了利用功率放大器的非线性实现信号识别的有效性。但该方法假设输入的信号采用相同的体制,且识别效果受信噪比、相空间参数影响较大。文献[12]对此过程进行了详细的理论分析与解释。在此基础上,许丹等[13]提出了基于相空间交叉关联积分的辐射源个体识别方法,该方法具有较高的鲁棒性。但当辐射源个数增加时,交叉关联积分的计算量呈平方次增加,系统实现难度大。此外,还有学者通过比较重构矢量的概率密度[14]、相轨迹形状[15]、重构矢量质心的概率分布[16]等方式实现基于相空间的特定辐射源个体识别。然而,上述方法均是在高维空间中提取指纹特征,运算量较大、效率较低。对此,文献[17]提出采用奇异值分解的方法提取相空间中的低维特征作为个体身份的辨识依据。此外,基于点云的深度学习方法同样可以用于从相空间中提取辐射源个体指纹特征[18]。然而,由于深度学习端到端的“黑盒”特性,指纹特征难以与硬件特性相关联,可解释性较差。

综上所述,现有的基于非线性动力学的方法面临三个问题:一是重构矢量的维数较高,样本信号长度长,计算难度高;二是识别率随着噪声的增加急剧下降,鲁棒性较差;三是缺乏理论基础,可解释性较差。针对上述问题,本文提出了一种基于重构吸引子的辐射源个体识别框架,并给出一种基于等距映射(isometric mapping, Isomap)的辐射源个体识别方法。该方法利用Isomap在重构相空间中提取重构吸引子作为辐射源指纹特征,在此基础上利用核函数支持向量机(kernel support vector machine, KSVM)实现个体辨识。实验表明,本文所提出的方法计算量小、能够快速地识别辐射源个体,并具有较好的鲁棒性。

本文的创新工作主要包含三个方面:一是提出基于重构吸引子的辐射源个体识别的框架;二是基于所提框架,提出了一种基于Isomap重构吸引子的方法,并利用KSVM实现了个体身份识别;三是仿真和实测数据实验证明该方法相比于其他基于相空间方法具有更好的识别效果与更高的识别效率。

1 基于重构吸引子的辐射源个体识别框架

一般的电子信息系统,在正常的工作模式下都是稳定的,即系统具有朝着某个稳态发展的趋势[11]。这个稳态在系统科学中称为吸引子(attractor),能够反映系统的非线性动力学特性。在辐射源系统中,吸引子蕴含着辐射源硬件的“不完美性”,可以作为辐射源个体识别的依据。

相空间(phase space)是用以表示出一个系统所有可能状态的空间,即系统每个可能的状态都对应着相空间中的某一相点。吸引子描述着系统的稳定状态,是系统状态集合的子集。因此,为完成个体识别任务,需在系统相空间中提取系统吸引子,并对其进行分类识别。考虑到难以直接观测到每个子系统的实时状态,难以直接获取辐射源系统的真实相空间、吸引子,只能依赖于从观测序列中重构。基于重构吸引子的辐射源个体识别框架如图1所示。

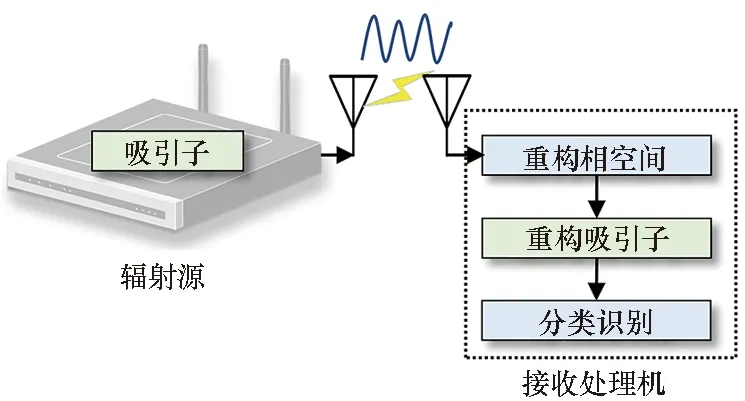
图1 基于重构吸引子的个体识别算法框架Fig.1 Framework of the SEI method based on reconstructed attractors

首先利用相空间重构技术从观测信号中重构系统相空间。再利用流形学习技术,从重构相空间中重构系统吸引子。最后利用重构吸引子完成个体识别任务。根据Takens嵌入定理[19],重构相空间与系统吸引子之间具有微分同胚的等价关系。流形学习技术在一定约束条件下将高维数据映射至低维空间,保证重构吸引子保留了重构相空间非线性动力学特性。因此,重构吸引子与系统吸引子具有一定的等价关系,同样能够反映辐射源的非线性动力学特性,蕴含着硬件独一无二的“不完美性”,可以作为个体身份辨识的依据。其次,重构吸引子中蕴含着整个系统的状态及其转移规律,能够完整地表征系统的非线性动力学特性,改善指纹特征“片面性”的不足,提升算法的适用范围。此外,相较于重构相空间,重构吸引子维度低,运算量小,更利于个体身份的快速辨识。

2 基于Isomap的辐射源个体识别技术

在基于重构吸引子的辐射源个体识别框架下,本节提出一种基于等距映射的辐射源个体识别方法。该方法利用延迟坐标技术重构系统相空间[19]。在重构相空间的基础上,采用等距映射的方法重构吸引子,并将其作为系统身份辨识的依据。算法的基本流程如图2所示。

图2 基于Isomap的辐射源个体识别技术Fig.2 The SEI method based Isomap

2.1 延迟坐标重构技术

相空间分析是非线性动力学的基本手段,而相空间重构是相空间分析的基础,常用延迟重构法。根据Takens定理[19],系统中任一变量的演化都是由与之相互作用的其他变量所共同决定的,因而多个变量的信息可用任一变量的演化过程表示。延迟重构法就是把单变量时间序列嵌入一个新的坐标系中,重构得到的轨迹状态蕴含了原相空间所有变量的状态轨迹。Takens嵌入定理表明,只要满足m>2d+1,则重构的相空间与发射该信号的辐射源系统相空间微分同胚,即拓扑等价[19]。

对信号s(t)进行相空间重构,得到相空间

(1)

(2)

其中:τ为延迟时间;m为嵌入维数;矩阵中行向量xi为系统的一个相点,代表系统的某一状态;X中蕴含着整个系统状态的转移,反映系统的非线性动力学特征。

在延迟坐标重构技术中,两个关键参数τ与m的确定在很大程度上决定了重构相空间的质量,即重构相空间和吸引子的近似程度。

延迟时间τ的选取目标是使原时间序列经过延迟时间后可以作为相对独立的坐标使用。综合考虑现有延迟时间τ估计算法的准确度与复杂度,本文选取互信息法[20]估计延迟时间τ。在互信息法中,首先定义两个时间序列p和q分别为

[p,q]=[s(n),s(n+τ)]

(3)

其中,p代表时间序列s(n),q为其延迟时间τ的时间序列s(n+τ),二者所对应的系统分别为P和Q。令I(P,Q)为两系统的互信息熵,则有

(4)

其中:Pp(pi)和Pq(qj)分别代表系统P和Q中事件pi和qj的概率;Ppq(pi,qj)为事件pi和事件qj的联合分布概率;互信息熵I(P,Q)的大小代表在已知系统s(n)的情况下,系统s(n+τ)的确定性大小。由式(3)和式(4)可知互信息熵与延迟时间τ紧密相关,可记为I(τ)。I(τ)的极小值表示了s(n)与s(n+τ)最大可能的不相关。因此选择I(τ)的第一个极小值所对应的延迟时间τ作为最优延迟时间。

嵌入维数m的选取目标是尽可能保证系统吸引子的几何结构在重构相空间中被完全打开。综合考虑现有嵌入维数估计算法的精度与复杂度,本文采用改进的伪最近邻点的改进方法,即Cao氏方法[21]确定嵌入维数m。在重构相空间的过程中,随着嵌入维数m的升高,吸引子的结构被逐步打开,低维投影所导致的伪近邻点数目逐渐减少,直至吸引子结构被完全打开,此时重构相空间中不存在伪近邻点。因此,定义描述距离变化规律的判断指标,即

(5)

其中,E(m)统计了整个重构相空间的距离比,可以表示为

(6)

2.2 等距映射

等距映射是流形学习中的一种无监督算法,主要应用于非线性数据降维。该算法采用最短路径距离度量两点间的距离,在保证任意两点之间测地线距离不变的约束下,对重构相空间进行降维,从而提取低维几何结构。等距映射的条件约束可以表达如下

(7)

其中,pi,j代表高维空间中两个样本点xi、xj之间的测地距离,即两节点间最短路径的距离,表示为

(8)

其中,xu、xv表示样本点xi、xj间路径上的节点。路径起始点为xi,终点为xj。yi、yj为二者在低维空间的投影。等距映射可以等价于解决凸优化问题[22],即已知高维空间中样本点两两之间的距离,尝试在其低维空间投影上找到一组新的样本点,使得降维后两点间的欧式距离与其在高维上的测地距离相等。

将等距映射应用于重构辐射源系统吸引子,首先需要根据专家经验预先设定最近邻点数k,并基于欧式距离为每个相点xi选取并连接其最邻近的k个邻居点,构成重构相空间的连通图G,表示为

G=(V,E)

(9)

其中:V为连通图的顶点,即重构相空间的相点;E为连通图中的边,描述了相点间的近邻关系。

随后,基于连通图G构建重构相空间所对应的邻接矩阵K。邻接矩阵K是表示顶点之间相邻关系的矩阵,为一个N-(m-1)τ维的方阵,可表示为

(10)

其中,kij∈{0,1}为邻接矩阵K中的第i行、第j列元素,表示重构相空间中第i个相点与第j个相点间的相邻关系。

基于Dijkstra算法计算连通图G中任意两点的测地距离,如式(8)所示。令pij代表第i个相点与第j个相点的测地距离,则距离矩阵为

(11)

为实现空间降维,计算距离矩阵P的内积矩阵B为

(12)

其中,J=IN-(m-1)τ-eeT/[N-(m-1)τ]且e=[1,1,…,1]T。而后对内积矩阵B进行奇异值分解,表示为

B=UΛVT

(13)

其中,Λ为特征值矩阵,V为特征向量矩阵。最后,取特征值矩阵的前d项,可得降维矩阵为

(14)

2.3 分类识别

经过等距映射后,得到重构吸引子

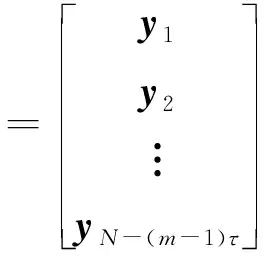
(15)

(16)

矩阵Y则可看作辐射源的状态序列。至此,对辐射源个体身份的辨识可以转化为对系统状态序列的辨识。当不考虑状态的转移过程,系统状态序列退化为系统状态集合,即通过对状态集合分析,识别辐射源个体身份。

本文采用KSVM对高维特征进行分类。支持向量机(support vector machine, SVM)是一种定义在特征空间上的间隔最大的线性分类器,能够在有监督的条件下出色地寻找到分类所需的超平面。而KSVM在SVM的基础上引入核函数,将SVM推广到更复杂的模型,能够寻找到分类所需的超曲面,更适用于辐射源个体识别任务。

综上,基于重构吸引子的辐射源个体识别算法可以归纳为四步:第一步对输入的信号进行归一化化处理;第二步相空间重构的核心在于选择合适的延迟时间与嵌入维数以保证重构相空间与辐射源系统吸引子拓扑等价,即二者微分同胚;第三步采用等距映射重构系统吸引子,以表征辐射源系统的非线性动力学特性;第四步利用KSVM分类器实现辐射源的个体身份识别。

3 仿真实验与分析

3.1 数据集

无意调制是器件的非理想性导致的,如数模转换器、成型滤波器、高频振荡器、功率放大器等都会产生不同程度的无意调制。不同硬件的非理想性中贡献最多的是放大器的非线性。根据文献[13],辐射源的非线性特性模型可以表示为

(17)

其中,α=[α1,α2,…,αn]为辐射源的非线性参数。本实验中设置6个辐射源{ci,i=1,2,…,6},α参数如表1所示。

表1 仿真辐射源非线性参数Tab.1 Nonlinear parameters for simulation emitters

3.2 系统稳定性验证

本节采用最大Lyapunov指数(largest Lyapunov exponents,LLE)验证辐射源系统产生信号的稳定性[10],进而推测辐射源吸引子的构型,辅助辐射源个体识别任务。LLE表征了系统在相空间中相邻轨道间收敛或发散的平均指数率,是用于辨识系统稳定性的特征之一,其表达式为

λmax=max(λ1,λ2,…,λm)

(18)

其中,λi为第i维方向上的Lyapunov指数,其表达式为

(19)

其中,d0为初始时刻相轨迹间的距离。经过t时刻后,距离变化为dt。λi描述了第i维方向上相邻相轨迹距离的增长率。当λmax>0时,系统为发散的、不稳定的,且最终状态为混沌运动;当λmax=0时,系统的最终状态为周期性运动;而当λmax<0时,系统为内敛的、稳定的,且最终收敛到稳定的平衡点。

为验证辐射源系统的稳定性,本文计算了6个辐射源的最大Lyapunov指数。每个辐射源采用200个样本,分别计算每个样本的LLE,而后对样本间数值取平均,结果如图3所示。忽略计算机带来的数值误差,辐射源系统的LLE为0,证明系统最终状态将呈现为周期性运动。因此可以推测系统吸引子为一极限环,即相空间里的一条闭合的、周期性的轨迹[10]。

图3 辐射源的平均最大Lyapunov指数Fig.3 Average largest Lyapunov exponents for emitters

3.3 重构相空间

本文采用坐标延迟重构法重构系统相空间。首先利用互信息法估计延迟时间τ[20],实验结果如图4所示。

图4 估计延迟时间Fig.4 Estimation of delay time

互信息法通过信息论和遍历论的知识,计算延迟时间。图4中曲线为互信息熵曲线,当其第一次下降到较小值时对应的延迟时间为最佳延迟时间。针对本文中6个辐射源,最佳的延迟时间τ=2。

在确定延迟时间τ=2基础上,采用Cao氏方法估计嵌入维数m[21]。该方法通过不断增大嵌入维数,计算虚假最邻近点比(E1指数)的方式寻找最佳的嵌入维数。实验结果如图5所示。

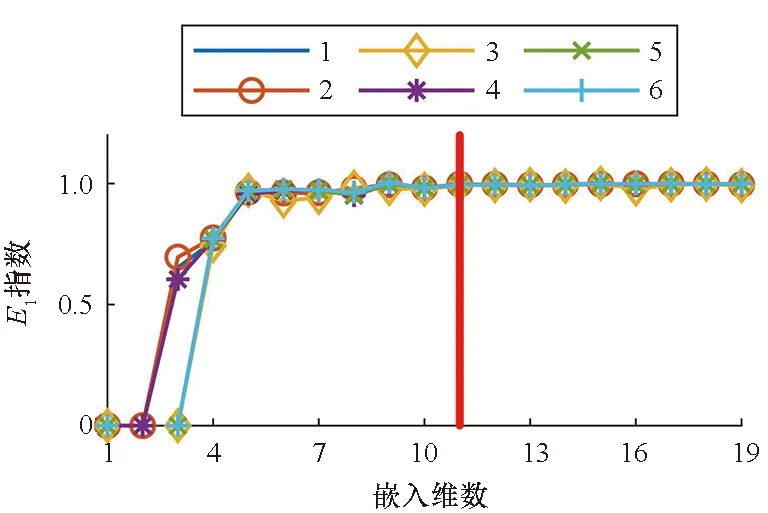
图5 估计嵌入维数Fig.5 Estimation of embedding dimension

由图5可知,当嵌入维数m=11时(红线所示),E1指数基本维持稳定,可以认为此时吸引子结构已经完全打开,即重构相空间中内蕴着系统吸引子结构且重构相空间与吸引子微分拓扑等价。

在确定延迟时间τ=2、嵌入维数m=11后,利用式(1)和式(2)中的延迟坐标技术重构相空间X。

3.4 算法可解释性

在重构信号相空间后,利用Isomap算法重构系统吸引子[22]。根据Takens定理[18],当m≥2d+1时,系统在相空间中完全展开,因此可以推断系统固有的维数d≤5。因此在降维的过程中,设置目标维数为d=5。为了直观地描述系统状态之间的差异,分别从高维空间的不同切面观察不同辐射源的状态分布情况,如图6和图7所示。

图6 无噪声时辐射源个体重构吸引子Fig.6 Reconstructed attractors for emitters without noise

图7 35 dB时辐射源个体重构吸引子Fig.7 Reconstructed attractors for emitters with 35 dB

图6、图7中不同颜色代表不同的辐射源个体。不同辐射源的重构吸引子在高维空间中分布在不同的区域。这意味着可以通过合理地划分高维空间,使得不同的子空间对应不同辐射源的重构吸引子,进而实现个体身份识别。此外,辐射源1、辐射源2、辐射源3在高维空间中的距离相对于辐射源4、辐射源5、辐射源6更大,这是因为前三个辐射源的功率放大器非线性系数的差异比后三个辐射源的功率放大器的非线性系数差异大,进而使状态差异更大。对比图6与图7可以看出,无噪声情况下,系统的状态更为稳定;而当存在噪声时,系统的相点会发生偏移,且偏移的程度与信噪比相关。

3.5 算法有效性

本文选择KSVM分类器对高维特征进行分类识别实验,在无噪声的情况下,利用80%的数据对分类器进行训练,20%数据作为测试集。训练后,KSVM对特征空间的划分效果如图8所示。

图8 KSVM划分特征空间效果图Fig.8 Division of feature space via KSVM

图8中不同颜色不同形状的标志点代表不同辐射源的系统状态,栅格点的不同颜色代表在此分类器中,该高维点所归属的辐射源序号。从图中可以看出,KSVM能够按照一定的特征结构对高维空间进行划分,保证不同子空间覆盖不同辐射源的系统状态,且划分空间中的决策面是软决策面,具有一定的鲁棒性。

3.6 算法鲁棒性

下面对6个辐射源的识别率进行实验。信噪比的范围是15～35 dB,识别率结果如图9所示。

图9 不同SNR的识别结果Fig.9 Recognition results of different SNR

图9中不同颜色代表不同的辐射源个体。相比而言,前三个辐射源的识别性能优于后三个辐射源的识别性能。这同样是由于前三者系统的差异性大,与有效性测试中的结果相一致。

在基于相空间低维表征的辐射源个体识别方法中,选取文献[17]及其改进方法作为对比方法。在对比算法中,同样地利用延迟重构技术进行相空间重构。而后直接对相空间进行奇异值分解(singular value decomposition,SVD),或对相空间进行二维奇异值分解[23](two-dimension singular value decomposition,2D-SVD),并将所得奇异值向量作为辐射源的特征向量。最后,采用K最近邻(K nearest neighbors, KNN)分类器对个体身份进行辨识,实验结果如图10所示。

图10 本文方法与其他方法的对比Fig.10 Comparison between the proposed method and other methods

从图10中可以看出,2D-SVD方法优于SVD方法,但两者都逊于本文算法。奇异值代表矩阵在不同向量上的投影。在进行SVD分解时,列向量的信息有所丢失,即辐射源系统状态间的联系丢失,而2D-SVD对列向量的信息保留更多,因此性能更好。但二者的识别性能都逊于本文算法,这是由于本文采用等距映射还原辐射源系统的吸引子,最大限度地保留了辐射源系统的动力学特性,并尽量减小观测带来的影响。

3.7 算法适应性

同样地,在利用互信息法与Cao氏方法估计得到延迟时间τ=2、嵌入维数m=13后,利用延迟坐标技术重构相空间。在重构信号相空间的基础上,利用Isomap算法重构系统吸引子。根据Takens定理[13],当m≥2d+1时,系统在相空间中完全展开。因此可以推断系统固有的维数d≤6。因此在降维的过程中,设置目标维数为d=6。最后,采用KSVM分类器辨识重构吸引子对应辐射源身份。实验结果如图11所示。

图11 不同调制方式的识别结果Fig.11 Recognition results of different modulations

由图11可知,本文算法同样能够完成2ASK、4ASK、2FSK、4FSK、BPSK、QPSK等调制信号的个体识别任务。但同时注意到,有意调制增加了系统吸引子动力学特性的复杂程度,进而导致重构吸引子结构更为复杂,分类识别难度增大,识别效果有所下降。

4 实测实验与分析

4.1 数据集

实测实验采用6台软件无线电设备(universal software radio peripheral, USRP)分别发射正弦信号。实验环境如图12所示。

图12 实测数据采集环境Fig.12 Environment of collecting signals

4.2 重构吸引子可视化

基于互信息法[20]与Cao氏方法[21]在确定延迟时间τ=1、嵌入维数m=5后,利用延迟坐标技术重构相空间。由此推断系统固有维数d=2,并采用Isomap算法重构系统吸引子。实验结果如图13所示。

图13 实测辐射源重构吸引子Fig.13 Reconstructed attractors for real-world emitters

由图13可知,实测辐射源的重构吸引子构型与图6、图7中仿真辐射源重构吸引子构型相似。这一实验结果验证了本文理论推导的正确性,并进一步证明了基于重构吸引子辐射源个体识别技术的可行性。同时注意到,辐射源5与辐射源6的重构吸引子在空间分布重合度较高,即二者指纹特征相近。

4.3 算法识别能力

进一步采用KSVM分类器对重构吸引子的身份进行辨识,识别结果如图14所示。由图14可知,本文方法可以以较高的识别率完成6台USRP设备的个体识别任务。由于实测辐射源重构吸引子间差异不同,不同个体的辨识效果不同。尤其辐射源5与辐射源6的识别准确率相对较低,这是由于二者重构吸引子在特征空间中重叠度较高,彼此容易混淆。该结果与图13中的分析结论相同。

图14 本文方法对不同辐射源的识别效果Fig.14 Recognition results of different real-world emitters

5 结论

本文构建了基于重构吸引子的辐射源个体识别框架,该框架从非线性动力学角度对辐射源身份进行辨识,能够以更低的维度描述辐射源系统的动力学特性,并具有更高的可解释性、更好的识别性能以及更强的噪声鲁棒性。在此框架基础上,提出了一种基于Isomap重构吸引子的算法。并用实验对重构吸引子的可解释性、有效性和鲁棒性进行检验。

但同时注意到本文所提出的基于Isomap重构吸引子的算法只是在基于重构吸引子的辐射源个体识别技术框架内的初步尝试。算法仍具有一定的局限性,如对通信信号有意调制的适应性较弱。在未来研究中,如何通过优化重构相空间、重构吸引子、分类识别三个核心步骤,提升算法的适用范围,仍需要更进一步的研究。