GNSS信号功率增强对调零抗干扰接收机的性能影响*

陈飞强,孙一凡,唐小妹,欧 钢

(国防科技大学 电子科学学院, 湖南 长沙 410073)

全球导航卫星系统(global navigation satellite system, GNSS)在军事和民用领域应用广泛,但其精度和可靠性一直受到电磁干扰的威胁。通常情况下,到达接收机的卫星信号功率比热噪声小20～30 dB。研究表明,辐射功率为1 W的干扰源即可使5 km范围内的P码接收机和15 km范围内的C/A码接收机无法正常工作[1]。

在系统层面,为提高目标区域内所有接收机的抗干扰能力,可采用功率增强策略提高卫星上导航信号的播发功率。而当采用点波束技术将功率增强限定在特定区域时,当前的GPS Ⅲ卫星可将信号功率增强20 dB[2]。在北斗三号系统中,针对北斗卫星也进行了功率增强的设计。随着导航卫星星座由中高轨向低轨发展[3-5],可以预见,未来导航卫星播发的信号功率将进一步增强。

在用户层面,接收机终端可集成干扰抑制模块提升抗干扰能力。在众多的抗干扰技术中,基于天线阵的自适应调零技术被证明是最有效的抗干扰手段之一[6-7]。自适应调零天线具有抗干扰能力强、实现代价小、便于与普通接收机集成(只需将普通接收机的天线替换为调零抗干扰天线即可)等一系列优点,得到了广泛应用[8-9]。

在实际的应用场景中,为有效应对电磁干扰的威胁,在系统层面和用户层面同时采取抗干扰措施将是一种很好的选择。为此,首先建立调零抗干扰接收机抗干扰能力分析模型,并定量分析信号功率增强对调零抗干扰接收机抗干扰性能的提升效果,研究成果可为卫星功率增强量的优化设计以及终端抗干扰设计提供参考。

1 接收机抗干扰能力分析模型

调零抗干扰接收机的抗干扰性能与具体的使用场景密切相关,卫星信号和干扰的数目、功率、入射方向等都会影响接收机的抗干扰性能。此外,即使在给定场景下,当前对接收机极限抗干扰能力也缺乏统一的定义,为简化分析,本文以信号接收载噪比高于接收机灵敏度时可容忍的最大干扰功率作为接收机的极限抗干扰能力。

接收机的极限抗干扰能力取决于硬件的线性度以及抗干扰算法的性能。硬件的非线性将产生交调、杂散、量化噪声等,这些分量一旦产生,将难以通过信号处理的方法进行消除,其效果等价于抬高了接收机的噪底,使信噪比恶化。硬件非线性主要包括射频模块的三阶交调失真以及模数转换器(analog to digital converter, A/D)量化损耗[10]。抗干扰算法的性能主要是指算法对干扰的抑制程度以及对信号的处理增益或损耗(调零算法未对信号方向的阵列响应进行约束)。干扰未充分抑制产生的干扰残余将等效抬升噪底,对信号的处理损耗将直接降低信号功率,两者均会导致信噪比恶化。信号捕获跟踪前接收机各个环节引起的信噪比损耗示意图如图1所示。

对三阶交调损耗、A/D量化损耗以及抗干扰算法损耗进行建模,可以得到接收机抗干扰能力分析模型如图2所示。图中:(C/N)i为进入接收机的初始载噪比;N0为初始的噪声谱密度;N′0为将三阶交调分量等效为热噪声后的噪声谱密度(由于接收机前端增益的大小并不影响信噪比,为简化分析,假设增益为1);L1为三阶交调失真引入的损耗;N″0为将A/D量化噪声等效为热噪声后的噪声谱密度;L2为A/D量化引入的损耗;(C/N)o为接收机输出载噪比;Xs和XJ分别为信号和干扰参数矢量,包含信号/干扰数目、功率、导向矢量等参数;Th为接收灵敏度。在给定场景下,若输出载噪比大于等于接收灵敏度,则判定接收机可容忍相应的干扰功率。下面对每个环节进行具体分析。

图2 接收机抗干扰能力分析模型Fig.2 Analysis model of receiver′s anti-jamming ability

1.1 三阶交调引起的信噪比损耗模型

三阶交调是三阶交调截取点(third-order intercept point, IP3)的简称,是衡量射频或微波系统线性度或失真度的重要指标[10]。实际系统中,当两个(或多个)载频信号经过非线性器件时,其输出信号将包括多种频率分量。其中三阶交调分量的频率与载频信号接近,一般分布在滤波器的通带内,不会被滤波器抑制。

进入接收机的干扰强度越大,其对应的三阶交调分量也越大,三阶交调分量落在信号带宽内时,其效果等价于抬高了噪声的噪底,使信号的信噪比恶化。

给定接收机射频前端的输出三阶交调截取点功率和输入三阶交调截取点功率,则三阶交调分量的功率PIP3与接收机输入功率Pin的关系为:

PIP3=OIP3-3·(IIP3-Pin)

=OIP3-3·IIP3+3·Pin

(1)

对于GNSS抗干扰接收机,在无干扰和弱干扰条件下,接收机产生的三阶交调分量很小,可以忽略。在强干扰条件下,则接收机的输入功率与干扰总功率近似相等,设干扰数目为M,且各个干扰之间互不相关,则有:

(2)

式中,PJ为干扰的总功率,Pjm为第m个干扰的功率。

将三阶交调分量等效为热噪声,则三阶交调引起的信噪比损耗可表示为:

(3)

式中:Q为抗干扰品质因数[11],由干扰和信号的频谱相关性决定;Rc为信号中扩频码的码率。

1.2 A/D量化引起的信噪比损耗模型

量化是将接收信号的幅度值集合从无穷大映射到有限的几个离散值,这个过程将引入误差,即量化噪声。对于实际的A/D器件,量化过程中除量化噪声外,还会产生谐波分量,若把谐波分量也当成噪声,则实际A/D的量化噪声功率要比根据其量化字长直接计算出来的大。为准确描述这一特征,通常用A/D有效位来描述实际A/D的量化性能。设A/D的有效位为b,则输入信号量化后的信噪比[12]为:

(S/N)=6.02·b+1.76

(4)

为了提高动态范围,GNSS抗干扰接收机一般采用量化字长较大的A/D(通常为12 bit甚至16 bit),在无干扰和弱干扰条件下,A/D的量化噪声几乎可以忽略。在强干扰条件下,量化噪声主要由干扰的量化噪声组成。若将A/D量化噪声等效为热噪声,则A/D量化等效抬高了噪底。

设接收机射频前端的带宽为B,则A/D量化引起的信噪比损耗可描述为:

(5)

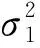
1.3 抗干扰算法引起的信噪比损耗模型

考虑阵元数目为N的任意阵型天线阵,假设K个互不相关的信号、M个互不相关的干扰从远场入射,则阵列抗干扰算法输入端的数据表示成复基带形式可描述为:

(6)

Rxx=E[x(t)xH(t)]=Rss+Rjj+Rnn

(7)

式中,E(·)表示数学期望,(·)H表示共轭转置,Rss、Rjj和Rnn分别代表信号、干扰和噪声的自相关矩阵,Psk为第k个卫星信号的功率,I为N维单位矩阵。

对于自适应调零算法,阵列权矢量的优化目标是使阵列的输出功率最小。据此可以得到自适应调零算法的最优阵列权矢量[13-14]为:

(8)

式中,w=[w1,w2,…,wN]T为N维阵列权矢量,c为N维约束矢量,通常取约束矢量的第1个元素为1,其余元素都为0。

根据阵列权矢量可进一步得到第i个卫星信号的阵列输出信干噪比[6]:

若将残余干扰等效为与信号同带宽的高斯噪声,经过抗干扰处理后,第i个卫星信号的载噪比可表示为:

(C/N)o=SINR+10lg(B)

(10)

进一步,抗干扰算法引起的信噪比损耗可表示为:

(11)

2 功率增强对接收机抗干扰性能提升效果的定量分析

考虑到卫星采用点波束进行功率增强时,对波束覆盖区域可能存在单重覆盖(即只有一颗卫星的点波束覆盖目标区域)和多重覆盖的情况,由于利用增强信号进行独立定位至少需要4颗卫星,限于论文篇幅,本文将聚焦功率增强信号4重覆盖的情况。

2.1 分析方法及参数设置

分析中用到的抗干扰接收机参数如表1所示,这些参数基本上按照实际的卫星导航抗干扰终端产品进行设置。

表1 抗干扰接收机参数Tab.1 Parameters of the receiver

卫星信号为北斗B3频点授权信号,信号初始电平(功率增强前)为-130 dBm。干扰为与卫星信号同频点的宽带高斯噪声干扰,其抗干扰品质因数为2.22。

前面提到,接收机的抗干扰性能与应用场景密切相关,为克服基于特定场景的评估方法的不足,采用蒙特卡罗仿真的思路。在每次仿真时,随机设置卫星信号和干扰的入射方向(考虑到实际中卫星信号一般从高仰角入射,而干扰一般从低仰角入射,因此限定卫星信号仰角大于30°、干扰仰角小于15°),并根据模型推算接收机输出的载噪比。

对于每一组给定的信号功率增强量和干扰功率,均进行L次(L设置为1 000)蒙特卡罗仿真实验,若L次实验得到的载噪比样本中有95%(2σ)超过接收灵敏度,则判定接收机可容忍此时的干扰功率,通过不断增大干扰功率,并重复上述步骤,最终可得出接收机的抗干扰极限能力。

2.2 实验结果及分析

在功率增强信号4重覆盖下,可以预见,针对增强的卫星信号,调零抗干扰接收机的抗干扰能力将得到提升。图3给出了接收机抗干扰极限能力与信号功率增强量的关系,不同的曲线代表不同的干扰数目。对于多个干扰的情况,均假设所有干扰的功率相等,纵坐标表示的是每一个干扰的功率,而非所有干扰的总功率。

图3 抗干扰极限能力与信号功率增强量的关系Fig.3 Relationship between ultimate anti-jamming ability and signal power enhancement

从图3可以看到,在信号功率增强之前,根据接收机参数和模型推算出接收机最大可容忍单个-24 dBm的干扰或者六个-35 dBm的干扰,换算成干信比(以信号初始电平为参考,即-130 dBm),分别为单干扰106 dBc、六干扰95 dBc。需要说明的是,本文选用的接收机参数并非性能最好的,若选用硬件线性度更优、接收灵敏度更高的接收机,得出的抗干扰极限能力将更高,但这并不影响论文的主要结论。从图中可以看出,随着信号功率增强量的增大,接收机的抗干扰极限能力也相应地提高。信号功率增强40 dB时,接收机抗干扰能力可提升到单干扰120 dBc、六干扰110 dBc。

图4进一步给出了接收机抗干扰能力提升量与信号功率增强量的关系。可以看出,接收机的抗干扰能力提升量与信号功率增强量近似呈线性关系。信号功率每增强10 dB,接收机抗干扰能力提升3～4 dB,而不是10 dB。

图4 抗干扰能力提升量与信号功率增强量的关系Fig.4 Relationship between anti-jamming ability improvement and signal power enhancement

为了对这一现象进行解释,表2以单干扰为例,给出了在干扰功率取极限值时,接收机各个环节的信噪比损耗。从表中可以看出,随着信号功率增强量的增加,在干扰功率取接收机可容忍的最大值时,A/D量化损耗和抗干扰算法损耗均变化不大,而三阶交调损耗迅速变大。信号功率增强带来的信噪比提升几乎都消耗在了三阶交调损耗上。而根据三阶交调的特性,从式(1)可以看出,干扰功率每增加1 dB,干扰产生的三阶交调分量增加3 dB,因此信号功率每增强10 dB,只能容忍进入接收机的干扰功率增加约3.3 dB,这与图4中的结果是吻合的。

表2 抗干扰接收机各个环节的信噪比损耗Tab.2 Signal noise ratio loss of each phase for the receiver

另外,当信号功率增强40 dB时,一般来说,此时信号的功率已经高于接收机热噪声,调零天线将在信号方向产生零陷,使得抗干扰算法的损耗变大(与增强之前相比)。但从表2可以看出,与增强之前相比,抗干扰算法引起的信噪比损耗并没有明显变化。这是因为在干扰功率取最大值时,三阶交调损耗达到了49.43 dB,等效将噪底极大抬升了,此时增强后的信号仍然掩埋在噪底之下,不会触发调零天线产生零陷。

前面分析了信号功率增强对接收机抗干扰极限能力的影响,下面对接收机在不同干扰强度下的性能进行分析。图5给出了不同干扰功率下(1个干扰),接收机输出载噪比与信号功率增强量的关系。从图中可以看到,接收机在无干扰以及干扰功率小于可容忍的最大功率时,输出载噪比曲线几乎是重合的,都是随着信号功率增强量的增加先变大后减小。在信号功率增强量为15 dB时,接收机的输出载噪比达到最大值。这是因为,干扰功率尚未达到可容忍的最大功率时,三阶交调损耗以及A/D量化损耗均较小,对噪底的影响不大。随着信号功率逐渐增大,调零天线在信号方向形成的零陷由浅变深,因而载噪比先增大后减小,对于这一现象更为详细的解释可参考文献[15]。

图5 接收机输出载噪比与信号功率增强量的关系Fig.5 Relationship between output carrier to noise ratio and signal power enhancement

结合图3和图5,可以得出以下结论:从提高接收机抗干扰极限能力的角度,信号功率增强量越大越好(基于当前及未来几年的工程实现能力,功率增强量暂考虑在40 dB以内),信号功率增强量越大,抗干扰能力越强。而从提高接收机非极限条件下的接收性能(载噪比、测距定位精度等)的角度,信号功率增强量并不是越大越好,信号功率增强15～20 dB时,接收性能最优。

3 结论

针对影响调零抗干扰接收机抗干扰性能的关键环节,建立了接收机抗干扰能力分析模型,涵盖三阶交调损耗模型、A/D量化损耗模型以及阵列抗干扰算法损耗模型。基于此模型,定量分析了信号功率增强对调零抗干扰接收机抗干扰性能的影响,研究结果表明:信号功率增强量越大,接收机抗干扰能力越强,信号功率每增强10 dB,接收机抗干扰能力提升3～4 dB。另外,从提高接收机非极限条件下的接收性能(载噪比、测距定位精度等)的角度,信号功率增强量并不是越大越好,信号功率增强15～20 dB时,接收性能最优。另外,对增强信号1～6重覆盖也进行了分析,结果表明本文的主要结论仍然成立。