利用主成分分析的通信调制识别通用对抗攻击方法*

柯 达,黄知涛,2,邓寿云,卢超奇

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 电子对抗学院, 安徽 合肥 230037; 3. 中国人民解放军31433部队, 辽宁 沈阳 110000)

通信信号自动调制识别(automatic modulation classification, AMC)技术作为信号检测和信号解调之间的重要步骤,可以自动识别接收信号的调制方式,提升认知电子战系统在非合作场景下实现高效频谱感知和频谱利用的能力[1],是适应复杂电磁环境的重要手段,也是近年来无线通信和电子侦察领域研究的重点课题。除传统的基于假设检验理论的AMC方法[2-4]和基于特征提取的方法[5-12],近年来学术界逐渐将目光转向了基于深度学习(deep learning, DL)的调制识别方法研究[13-18]。将DL方法应用到AMC问题中,DL可以自适应学习数据的有效表征,避免了人工设计特征的过程,加快了技术迭代的效率,同时大量的用频设备为数据驱动的DL方法提供了充足的数据支撑[19]。

但是,DL的脆弱性也一直为人诟病,现有DL模型虽然在许多领域取得了耀眼的成绩,但是存在一类针对DL模型的特殊攻击方式,可以实现对DL模型高效且隐蔽的攻击,这种攻击方式被称为“对抗样本”[20]。利用DL存在的固有缺陷,可以设计出一种特殊的极其微弱的扰动,将其添加到待处理的样本中,可以使原本表现良好的模型以很高的置信度对样本给出错误的处理结果[21]。由于添加的扰动极其微弱,人们难以察觉样本被做出了改动,因而难以预防。如果将对抗样本技术充分应用于通信信号波形的生成过程中,将会遏制未来智能化认知电子战系统的精确感知能力[22]。因此,有必要从通信信号对抗样本的生成和防御两方面展开研究。本文立足攻防结合,以攻促防,从对抗样本攻击的角度研究了一种通用对抗性扰动(universal adversarial perturbations, UAP)的生成方法,在基于DL的调制识别模型中初步验证了算法的可行性和有效性。

自2014年Szegedy等首次发现对抗样本现象后,次年,Goodfellow等进一步解释了对抗样本存在的原因,并提出了快速计算对抗样本的快速梯度符号法[23](fast gradient sign method, FGSM)。Lü等在文献[24]中提出了一种统一求解对抗样本的理论框架,为后续对抗样本的研究奠定了基础。前期关于对抗样本的研究主要集中在图像和语音领域中。2019年,文献[25]首次研究了针对基于DL的通信信号调制识别模型的对抗样本攻击,验证了其可行性;文献[26]在通信信号对抗样本攻击的基础上,尝试了将对抗训练的思想引入对抗样本防御中。文献[18]中,Lin等在开源调制识别数据集中验证了现有的多种对抗样本攻击方法的可行性。Kim等在多种场景下考虑了通信信号对抗样本受信道影响的因素,提出了适应真实信道场景的对抗样本攻击方法[27-29]。尽管上述工作已经对调制识别任务中的对抗样本进行了充分的探索,但是上述工作采用的对抗样本攻击方法每次实施对抗样本攻击时均需要针对每一类调制每一个样本计算一次对抗性扰动,难以满足通信过程自适应和实时性的要求。UAP可以针对目标模型,仅以部分样本为基础,生成一个特定的扰动,输入模型中的所有样本加上该扰动后,均能达到对抗攻击的效果。“通用”指的是生成的扰动可以破坏模型对尽可能多的调制方式与输入样本的识别过程。通用对抗性扰动可以在离线的条件下生成,实际通信过程中只需将该扰动添加到待发射的信号中,便可得到通信信号的对抗样本,满足实时性的要求。

文献[30]最早在图像处理问题中提出了UAP的生成方法,验证了UAP在不同数据之间存在很好的通用性,即使对于表现良好的神经网络,其输入的大部分数据加上微小的UAP,都能被网络以很高的置信度识别成错误的结果;对UAP的存在性给出了经验性的解释,认为UAP揭示了基于DL的分类模型的高维决策边界之间存在几何相关性,即在输入空间中存在单一的方向可以破坏基于DL的分类器的识别过程。其核心思想是采用迭代的方法去逼近文中所提出的表征几何相关性的方向。本文在文献[30]的基础上,首先建立了通信调制识别的系统模型,然后针对调制识别模型计算了攻击所需的最小对抗扰动。由于最小对抗扰动的方向垂直于分类边界,所以该方向可以用于表征分类界面的特性。在此基础上,提出了基于主成分分析(principal component analysis, PCA)的UAP计算方法,通过对计算得到的若干最小对抗扰动进行主成分分析,得到最能表征目标模型分类界面几何相关性的方向,从而得到对整个数据集具有普适性的通用对抗扰动。

1 系统模型

对抗样本攻击即在正常的通信过程中添加一段精心设计的扰动,在尽可能不破坏合作通信过程的基础上,使得基于DL的非合作通信系统难以识别信号,从而达到保护合作通信的目的。对抗样本攻击的系统模型如图1所示,主要由通信发射机、接收机和通用对抗扰动UAP发射机构成。

图1 通信系统中对抗样本攻击的系统模型Fig.1 System model for combating a sample attack in a communication system

在正常的通信过程中,发射信号x经信道Htr传输至接收机,此时信号s容易被非合作系统截获。为了降低被智能侦察系统识别的概率,UAP发射机会同时辐射通用对抗扰动δ,此时接收方和侦察系统接收到的信号分别为

(1)

其中:s为发射信号,δ为对抗性扰动UAP;Htri为s所经过的信道,Hari为UAP传输的信道;n为高斯白噪声。侦察系统会对接收信号xar进行调制识别,并进一步进行解调解译等工作。在正常通信信号中假如对抗扰动δ的目的就是在尽可能保证自身通信不受影响的前提下,使智能化侦察系统难以识别接收信号xar的调制,所以对抗性扰动UAP的能量要尽可能小。

1.1 通信信号智能调制识别模型

通信系统中,往往需要经过调制将基带信息负载到载波上实现远距离传输。AMC技术可以在未知先验信息的条件下,自动判断出通信信号的调制方式。

由于非合作系统无法知道接收信号是否含有对抗性扰动δ,所以上述问题可以简化为

xar=Htr2(s)+n

(2)

基于深度学习的调制识别的目的就是设计一个基于深度学习的分类器f(x;θ):X→C。其中X为输入空间,θ为分类器f的参数,C是待识别调制类型的数目。分类器f的识别结果为

(3)

用于分类的深度神经网络主要有全连接网络(fully-connected network, FN)、卷积神经网络(convolutional neural network, CNN)和循环神经网络(recurrent neural network, RNN)。本文采用目前主流的卷积神经网络结构ResNet18[31]作为实验的对象,详细的网络结构和参数设置如图2所示。

图2 基于ResNet18的调制识别网络结构Fig.2 Structure diagram of the modulation recognition network based on ResNet18

1.2 基于PCA的通用对抗性扰动模型

深度学习自身也面临鲁棒性差的问题,特别是容易受到对抗样本攻击。如式(1)所示,若非合作通信系统接收信号中带有通用对抗扰动δ,则智能侦察系统对接收信号xar的调制识别准确率将会严重下降。通用对抗扰动的定义是

f(xar+δ)≠f(xar)

(4)

并且要求式(4)对任意xar∈X均成立。设信号集X=[xar1,xar2,…,xarm]T抽样自接收信号的总体分布X。首先,分别计算X中的每个xari对分类器f的最小对抗性扰动δi[32],得到最小对抗性扰动构成的集合Δ=[δ1,δ2,…,δm]T。在L2范数的约束下,xari的最小对抗性扰动的方向δi可以理解为过xari计算分类界面法向量。为简化问题,首先考虑最简单的情况,即二分类线性分类器,其原理如图3所示。

图3 最小扰动原理图Fig.3 Schematic of the minimal perturbation

此时分类器f(x)=ωTx+b,其中ω为分类器权重,b为分类器的偏置。则法向量δi的表达式为

(5)

算法1 任意多分类器的最小扰动计算方法Alg.1 Minimal perturbation calculation method for arbitrary multiple classifiers

对每个样本计算得到的δmin构成矩阵Δ,再对矩阵Δ进行奇异值分解,即

Δ=UΣVT

(6)

算法2 基于PCA的UAP计算方法Alg.2 PCA-based calculation method for UAP

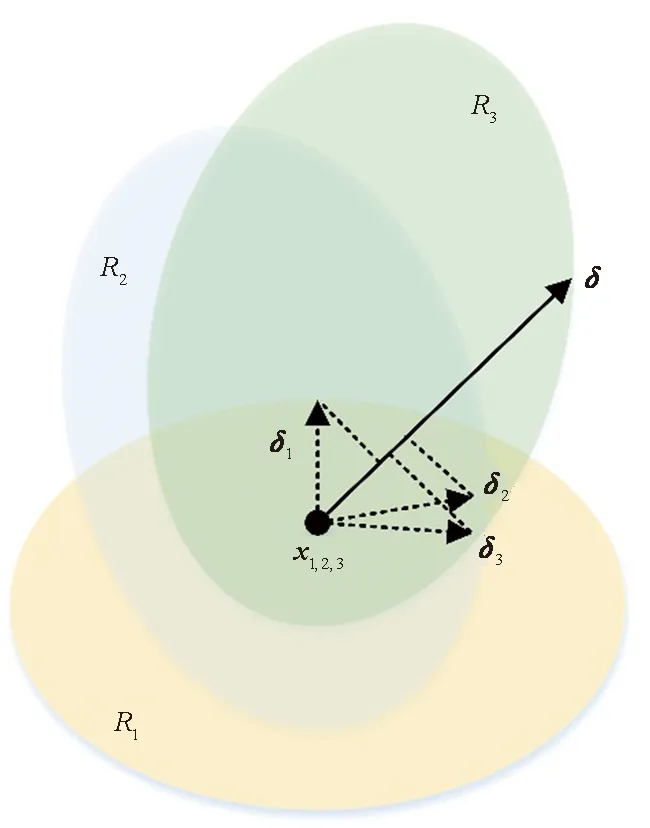
图4 基于PCA的通用对抗扰动算法原理图Fig.4 Schematic of a general adversarial perturbation algorithm based on PCA

2 实验验证

本节主要设计两个实验用于验证所提方法的性能。第一个实验是通过与算法3[30]对比,验证所提算法的先进性;第二个实验是分析不同抽样数量对本算法性能的影响。

2.1 基线方法介绍

采用文献[30]所提算法(见算法3)作为对比的基线方法。设X={x1,x2,…,xm}为抽样自总体数据集的部分样本集。其算法原理为:对X中的每一个样本迭代地建立通用扰动δ。如图5所示,每一轮迭代中都会把当前采样点对应的最小对抗扰动δi送入当前的扰动采样点xi+δ中,和之前计算出的通用扰动δ构成新的通用扰动。其中x1,2,3表示抽样的3个样本,R1、R2、R3分别表示x1,2,3对应的3个分类界面。通过不断修正,促使最终的通用扰动δ能够扰乱分类器对大部分样本的分类。

算法3 通用对抗扰动计算方法Alg.3 Universal adversarial perturbation calculation methods

图5 通用对抗扰动生成算法原理示意图Fig.5 Schematic diagram of the general adversarial disturbance generation algorithm

2.2 实验准备与数据集

所有实验均在NVIDIA GeForce GTX 3090 GPU上进行计算,通过pytorch1.10和cuda11.3实现。优化器为Adam,使用交叉熵损失函数进行训练,总训练次数为100次,学习率为10-5,设置early stopping策略。

实验所用数据来自开源通信信号调制识别数据集RML2016.04C,该数据集包含BPSK、QPSK、8PSK、16QAM、64QAM、BFSK、CPFSK、PAM4、WB-FM、AM-SSB、AM-DSB共11种调制类型,覆盖信噪比-20～18 dB,步进2 dB。数据集共162 060个样本,每个样本包含128点IQ数据。训练集、验证集、测试集按照7 ∶2 ∶1的比例划分。

2.3 攻击性能对比

对于计算得到的通用对抗性扰动δ,定义扰动-信号比(perturbation-signal ratio, PSR)衡量对抗性扰动相对于信号的强弱,用以评价对抗性扰动的“不可察觉性”,其计算公式为

(7)

其中,Pδ和Px分别代表扰动和信号的功率。同样地,对于算法攻击性能的评价,定义欺骗率(fooling rate, FR)来评价算法的优劣,其计算公式为

(8)

其中,f(xi)为识别正确的结果,(·)为指示函数,N为总样本数。FR的含义是,对于原本已经正确识别的样本xi,加入通用扰动δ后,被分类器误判,则认为欺骗成功。实验分别随机抽取50、500、5 000个样本生成了PSR为-20～0 dB的通用扰动,对已经训练完成的分类器进行攻击,测试样本数为16 206,实验结果如图6所示。

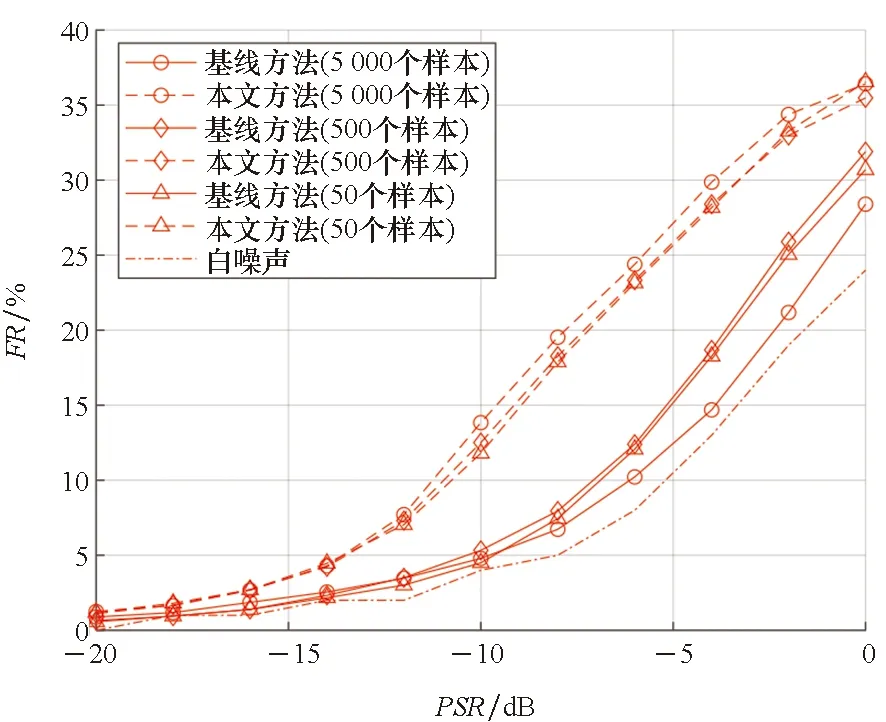
图6 欺骗率随PSR变化曲线Fig.6 Fooling rate curve with PSR

本实验对比了基线方法和白噪声的攻击性能。实验结果表明,同等PSR下,所提出的算法攻击性能全面优于基线方法。当PSR大于-15 dB后,所提方法的性能优势逐渐明显,同等欺骗率所需的扰动大小相对于基线方法可以降低4～6 dB。当PSR=0 dB时,所提方法的最高欺骗率为36.55%,基线方法的最高欺骗率为31.9%,所提方法性能提升了4.65%。

实验分别抽样了50、500、5 000个样本用于生成通用扰动,从结果看来,随着抽样数的提升,算法性能有微弱的提升,但是并不明显。其中,当抽样数为5 000时,基线方法的性能反而比抽样数为500时差。根据图5所示的通用扰动算法原理,随着样本抽样数的增加,对通用扰动δ的修正因素也会增加,但是每次修正因素只能保证对当前样本是有效的,而无法保证对样本整体有效。基线方法并没有设计相应的机制来约束修正因素对样本整体的攻击性能,所以当抽样数由500增加到5 000时,造成了欺骗性能的下降。而本文提出的方法,核心思想是提取了多个扰动的主成分,有效地避免了由于样本数增加带来的干扰因素。

2.4 通用扰动攻击性能受抽样数的影响分析

为进一步探究抽样数与算法性能的影响,设计了本实验进行研究。首先,抽取50个样本计算得到算法2中的输入矩阵Δ=[δ1,δ2,…,δm]T,然后对矩阵Δ进行奇异值分解。同步地,对50个高斯白噪声(Gaussian white noise, WGN)张成的矩阵计算奇异值。归一化的奇异值如图7所示由大到小进行排序。从图中可以看出,由WGN张成矩阵的奇异值按从大到小排列,奇异值曲线的下降速度缓慢,这符合随机噪声的特点,说明各个随机噪声向量之间不存在较强的相关性。相反,矩阵Δ的奇异值经过了一个快速的下降过程,下降的拐点在第5个奇异值附近,说明少数的奇异值张成的向量便能近似地表征整个矩阵的主成分,这也解释了通用对抗扰动存在的合理性,即由对抗性扰动构成的矩阵Δ中较大的奇异值张成的向量便能表征分类器脆弱性。

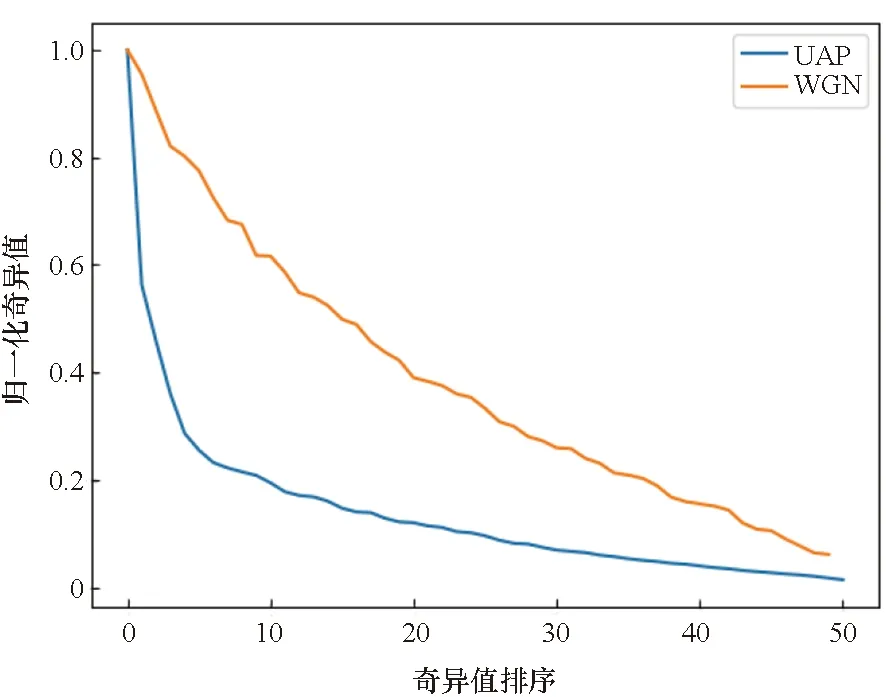
图7 矩阵Δ的奇异值Fig.7 Singular value of the Δ matrix

定义每个奇异值占总奇异值之和的比重为奇异值贡献度,第i个奇异值的贡献度计算公式为

(9)

通过计算,前24个奇异值的贡献度之和已经超过了80%,这说明可以用少数几个奇异值和对应的左右奇异向量来近似描述原矩阵。

基于上述结论,分别抽样1～50个样本用于生成通用对抗扰动,固定其PSR为-10 dB,攻击效果如图8所示。结果表明,随着抽样数的上升,欺骗率呈总体上升的趋势,当抽样数超过25后,欺骗率趋于稳定,实验结果与图7所示的推论相吻合,即仅需要25个样本所生成的通用对抗扰动便可实现较好的攻击性能,这也解释了2.3节中抽样数分别为50、500、5 000的性能差异并不明显的现象。

图8 欺骗率随抽样数变化曲线Fig.8 Curve of fooling rate with the number of samples

3 结论

针对基于深度学习的通信信号调制识别的应用场景,对其容易受到对抗样本攻击的脆弱性进行了研究。

1)提出了一种基于PCA的改进的通用对抗扰动生成方法,该方法可基于少量的接收信号生成一个通用的对抗性扰动,该扰动可以降低识别器对所有输入信号的调制识别准确率。通用对抗性扰动可以在离线条件下产生,然后实时添加到通信过程中,能够满足通信过程的实时性要求。

2)采用卷积神经网络中的代表结构ResNet18在开源调制识别数据集中进行训练并识别。采用本文提出的通用对抗扰动生成方法,分别抽取50、500、5 000个样本生成PSR为-20～0 dB的通用扰动,并将其添加到16 206个测试样本中,测试其欺骗率并与基线方法对比。实验结果表明,本文方法相对于基线方法具有明显性能提升,同等欺骗率所需的扰动大小相对于基线方法可以降低4～6 dB,最高欺骗率提升了4.65%。

3)对通用对抗扰动受抽样数的影响进行了分析和实验验证。首先分析了通用对抗扰动的合理性,并分别抽样1～50个样本对分析结论进行验证。实验结果表明对所使用的数据集合分类器,所提算法仅需抽样25个样本便可生成稳定的通用扰动,与理论分析相吻合。证明本文算法具有更优的攻击性能。