“问题提出”引领下的小学数学教学探微——以“多边形的面积”单元教学为例

吴琪芳

(南安市诗山中心小学，福建 南安 362300)

一、两种数学课堂形态的审思

“静悄悄的课堂”向来是小学数学教学的日常典型现象，研究者们从教学文化、教师行为、学生心理等方面作出了归因解释。笔者根据长期的教学经验，认为也可从学习认知的角度予以理解。数学教育于学生而言，既是一种“计算”也是一种“理解”，但是学生们长期以来囿于教师的教育教学理念，往往更重视计算公式的获得与应用，对于数学概念的本质理解则盲人摸象、浑然无感。如在《多边形的面积》教学中，学生们往往能做好通过公式的套用而“应答”各类题目，但是对于面积守恒、过程性推导、用已知解决未知的数学思想则一片混沌。于是就有了“不教也会”的倦怠式沉默与“教也不会”的苟安式沉默。这两种沉默形态使得数学课堂进入学生思维与心理深度缺位的学习样态。

“闹哄哄的课堂”则是近年来在践行新课改精神背景下的异化现象。为了纠偏“一言堂”现象，还学生以主体学习之姿，遂在学生的学习方式上作了多方面调适。但是，有的课堂为了彰显教师的“启发性”，于是就设计了一系列杂乱而浅层次的问题“满堂问”，问得学生兴高采烈却学无所得。或者是为了展现学生的“合作性”，于是各种课堂学习小组、学习讨论哗然而起，但是小组内部讨论的学科性、思维性则明显缺失。这种缺乏有效问题引领与真实思考的课堂教学，看似一片“生机”，实质上学生们往往陷入伪参与、假学习的困境。教师虽然应拒绝消极沉默的课堂，但是数学课堂又是高度要求学生们能有效性倾听、沉浸式思考、反思性分析的。闹哄哄的课堂有可能在喧嚣中让学生的数学思维滑入庸劣。

二、“问题提出”引领下的数学学习空间探视

那么，如何处理好其中的动静辩证关系，使得“静悄悄的课堂”从消极沉默走向深度参与，使得“闹哄哄的课堂”从浅虚浮松走向深实笃厚？笔者认为依托“问题提出”展开的数学教学与数学学习，不仅能弥合两种课堂的消极裂痕，也能为教师提供新的教学视角，为学生展示新的学习方式。

“问题提出”的能力，既能够敏锐学生的问题意识，从而强化对知识的深度理解，也能够深化学生的认知方式，化被动地“回答”预设问题为主动地发现、求解问题，进而延展学生们的学习机会与学习交往[1]。“问题提出”对于学生们的学习方式将产生以下几方面影响。

一是开放性的空间赋予学生深度学习的可能。刘加霞认为，小学数学教育“需要关注学生的朴素问题与思维过程”。[2]“问题提出”的教学理念将学生置入一个“没有具体题目”的情境，促使学生跳出传统的被动式接受知识，碎片化理解知识的学习局限，开始学会有意识地主动感知学科知识的本质与意义，整体且全面地理解知识之间的内在勾连。

二是情境化的空间赋予学生个性学习的可能。小学数学的问题形态往往呈现为单向度的“问”以促使学生去“解决问题”。[3]“问题提出”的教学方式则倾向在给予学生一种符合儿童经验的认知情境中，引导学生合理提出问题。化“别人的题”为“我提出的题”，变混沌式学习为探寻学科逻辑的学习。[4]

三是参与式的空间赋予学生交互学习的可能。每个学生往往会根据自身的生活经验、兴趣爱好、思考方式、学科理解等提出自身的问题。在此问题提出的过程中，学生们之间可以相互感知、理解对方的思维特色，从而在交流中建立起更好的合作方式，也可以在商讨辩驳中，形成“什么是好问题”的学习认知，从而进一步提升自身的学科思维。

三、“问题提出”引领下的小学数学教学实践——以“多边形的面积”单元教学为例

(一)在旧知新识的联结中引导学生提出问题

小学阶段的“面积”知识承接了从一维的线到二维的面再到表面积的学习，学生关于图形的认识核心主要聚焦于“图形各要素之间的关系”与“图形之间的关系”两个方面。在关于图形各要素之间关系的认知中指向的是关于测量方法的获得，在图形之间关系的认知中指向的是关于转化思想的习得。教师一般在“我要怎么教”的教学设计理念中，先导地设计学习方向，从而督促学生埋头赶路，循路而学。那么是否有可能引导学生抬头望路，带着清晰的问题意识去学呢？在五年级上册“多边形的面积”单元中，笔者创设了两个学科知识情境，引导学生自设问题，以激活他们的学习意识。

第一个教学镜头：用方格纸画上长方形与正方形，让学生据此提出一个数学问题并进行求解。学生根据已学过的知识，普遍围绕已给条件提出“写出下面各图形的面积”一类面积计算问题。在解决问题中，顺势总结“S=每行单位面积的个数×行数”【设计意图：通过自我问题设计，既是让学生形成对长方形、正方形计算方法的回忆，也是让学生在方格纸的直观感受中初步获取二维图形的量感。】

第二个教学镜头：用方格纸画上长方形、平行四边形、三角形、梯形，让学生据此提出一个数学问题并进行求解。此时，问题就多了，诸如“它们有几条边”“它们有什么不同”等，但就是不愿提“写出下面各图形的面积”一类问题。因为学生开始犯难了：平行四边形占的格子不整齐，三角形只有三条边，梯形长短不一，怎么能用此前总结的公式来套用呢？【设计意图：通过方格纸，直观地展示多边形的不同形态，对已提出的问题辨析其价值性，对未能或不敢提出的问题则解释其中可能的思维阻塞点。学生在认知冲突中不自觉产生数学猜想与探究诉求。】

(二)在学科认知的进阶中引导学生提出问题

小学的图形认识，主要经历了从一年级的直观感知到二年级的要素刻画，再到三年级的单位累加，直至五年级的图形转化。这一学习过程实质上是从图形认识到图形的度量的进阶过程。它指向的是教会学生如何从折一折、画一画等操作活动经验一步步升格、转化为问题解决经验。在五年级上册“比较图形的面积”栏目设计，其意义就是为了帮助学生形成基本的“转化”思想。于是，围绕“转化方法”与“转化应用”两个维度，笔者引导学生提出问题，以此深化对“转化”思想学科理解。

第一个教学镜头：让两位学生分别展示其动手操作计算平行四边形面积的方法，一个以一格一格地剪接拼凑方式，一个以整块剪接平移方式。据此，让学生针对两人的不同方式展开问题提出，并解释理由。【设计意图：在学生动手操作计算平行四边形面积的方法时，主要表现为对转化方法的无意识运用，如何敏锐其关于方法的清晰认知，从而进一步在观念上深化对转化意义的理解。通过问题设计与学生的自我阐述，学生开始自觉地意识到两种方法差异之后的关联性，在化不整为整之后实质上便是化新知为旧知。】

第二个教学镜头：有人说，从一组平行线上沿着直线减下来的一切形状都是梯形。以下五个图形面积相等，从(图1)中任选一个图形，你能用几种方式解释它们之间的面积相等。【设计意图：学生们在学习多边形面积时，往往较为擅长运用公式展开计算，但是对于公式的计算推理过程、图形观察与分析能力有所不足，空间观念较差，转化意识相对薄弱。教师利用几何画板帮助学生发现梯形统整多边形面积计算公式，让学生运用已学的公式或者推导方法，建构起内在的关系认知。】

图1

(三)在思维认知的节点处引导学生提出问题

徐立治先生认为，应当用思维的分析带动具体知识内容的教学，从而把数学课真正“教活”“教懂”“教深”。小学生的数学思维往往呈现为形象思维占主导，逻辑思维依附性强，发展性思维存在思维定势。因此，在学生容易陷入思维泥淖的节点处，可以通过有效的问题提出引领，从而帮助学生对自我的思维形态展开内向反思，学会富有数学性的思考。

一是在思维浅层处引导学生提出问题。小学生对于图形的理解往往容易拘泥于固有的平面认知，如图2的面积计算，学生只是单纯地记住了底×高，因而很容易计算为“8×6=48(cm2)”。这其实是学生的错误直觉引发的判断失误，而引发学生错误直觉的因素主要是两个，一是平行四边形的易变性使得学生容易将不同底的高同质化，二是数据的存在使得学生受到了干扰，容易从分析图形的学习意图陷入套用公式的学习意图。因而，教师可以提供图2引导学生观察、思考提出问题，教师进而对学生的问题进行思维梯度组织。

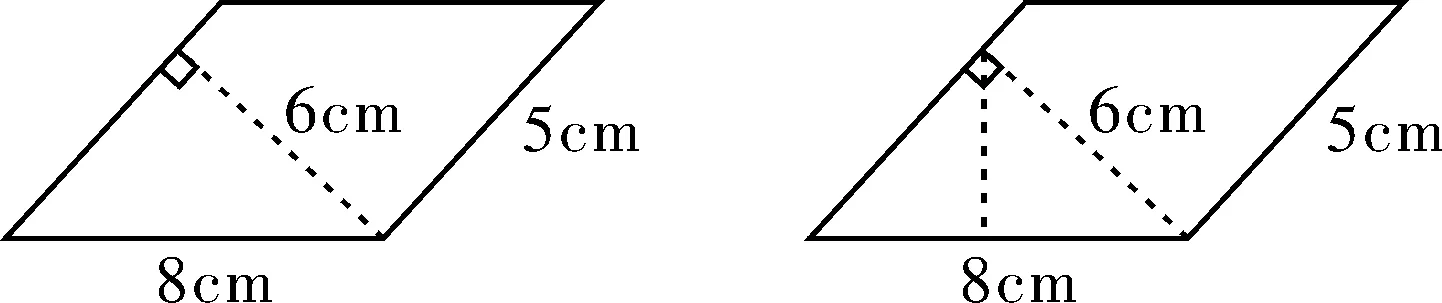
图2

二是在思维定势处引导学生提出问题。如典型习题：每相邻两个点之间的距离为1厘米。△ABC的面积是多少平方厘米？(图3)本题主要是考查学生在具体问题情境中的转化能力，学生们在无法获得三角形底和高的情境下，很容易转回基本的数方格的思维定势中。就此，盛童亮教师就将学生的几种典型错误解法与优质的解法予以整合(图4)，让学生观察不同的解法，并让学生说明不同解题思路的可能推理过程[2]。学生的问题提出意识既是一种对数据关系的想象，也是对逻辑路径的回溯。

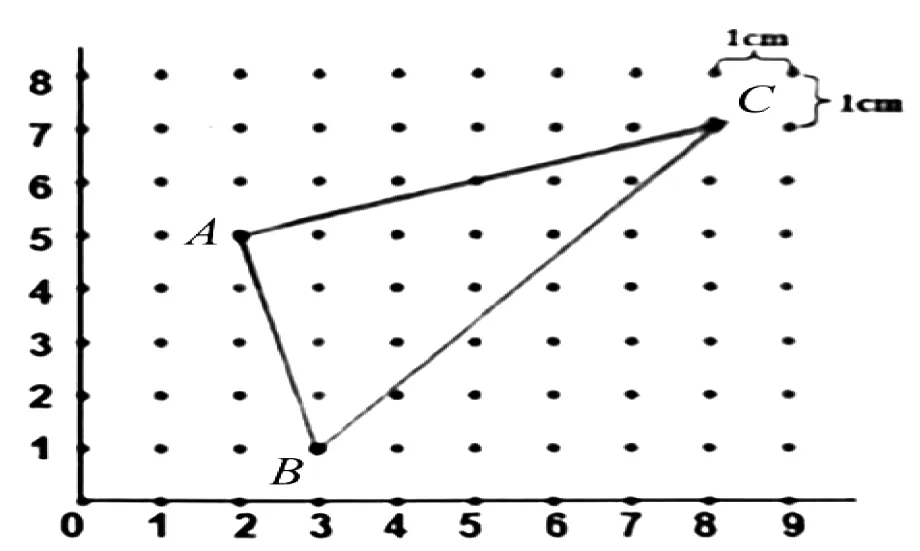
图3

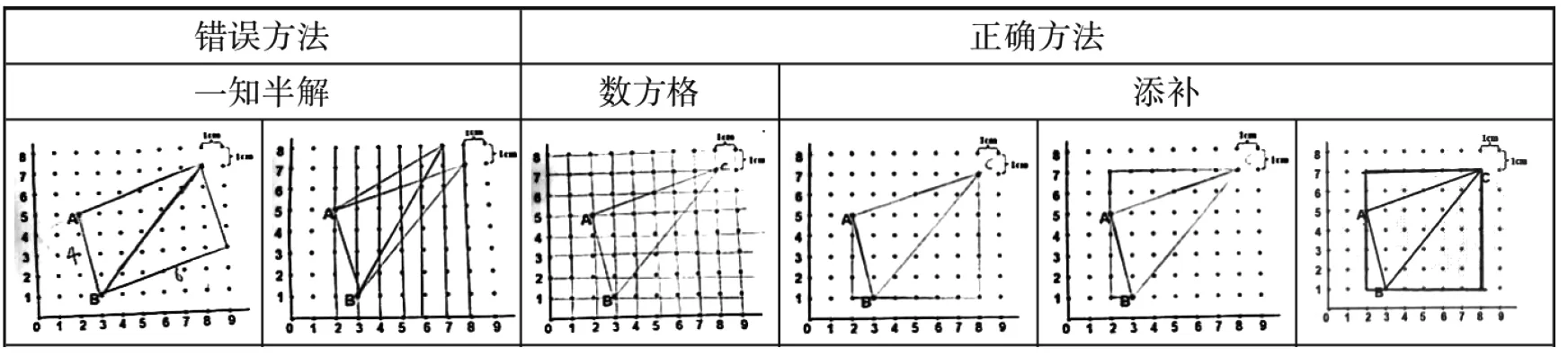
图4

四、在学习情境的构建中引导学生提出问题

张辉蓉等认为，基于“情境—问题”的教学模式，“问题提出”的教学设计可聚焦信息搜索—问题提出—问题解决—问题变身四个环节。为了让学生进一步理解平行四边形面积的本质，应准确理解“等底等高”的关系。于是围绕上述四环节，笔者展开“神奇的1/2”的“问题提出”教学设计。

一是让学生根据图5寻找各类数学信息，进而让学生就归纳的数学信息予以辨析：哪些在本图中可能是有意义的。

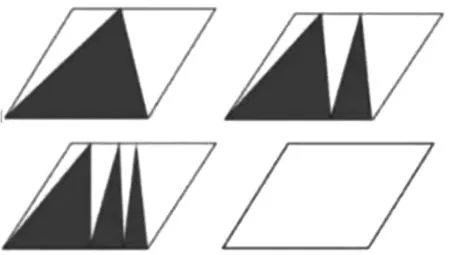
图5

二是引导学生就所搜集的信息，试着观察之间的可能联系，进而形成一些猜想。对此，为避免图形过于抽象导致思维难以挺近，教师可适当让学生对图形赋值，从而以算的多维方式推进对图形的抽象理解。

三是针对学生所提出的问题，教师鼓励学生大胆猜想图形中的数学关系，在对数学信息的一系列分析与验证中，鼓励其尝试用数学符号或者数学语言将数学问题风格化地表达出来。进而引导学生形成“我的问题清单”意识，学会清楚地意识到所面临的数学问题及其解决思路。

四是在前述基础上，引导学生就已有的“问题提出”的结构与关系，学会用数学眼光去认知、分析新的问题。如图6、图7所示，便是化静为动，引入移动点，引导学生借鉴前环节的问题解决过程，深化对新的问题的认知与解决。

图6

图7

综上，面对传统数学课堂的学习情态，引入“问题提出”的教学意识，生成学生“问题提出”的学习方式，将有助于师生在数学课堂中学会更加积极地倾听与更有意义的沉思。也期待将“问题提出”理念有效地落实到数学教育中，真正让学生学会“用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界”！