2023年全国新高考Ⅱ卷第21题的溯源与多角度探究

焦永垚

(兰州市第六中学,甘肃 兰州 730060)

1 试题呈现

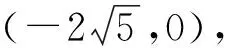
1)求C的方程.

2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于点M,N,且点M在第二象限,直线MA1与NA2交于点P．证明:点P在定直线上．

(2023年全国数学新高考Ⅰ卷第21题)

2 试题溯源

试题以双曲线为背景,考查学生的直观想象、逻辑推理、数学运算等核心素养．笔者发现,例1与以下几道题同根同源:

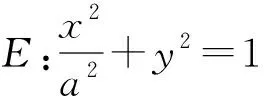
1)求E的方程.

2)证明:直线CD过定点．

(2020年全国数学高考Ⅱ卷理科第20题)

不难发现,例1与例2高度相似,不同点在于:1)两道题分别以双曲线和椭圆为背景;2)两道题第2)小题的条件和结论互换,即例1为例2的逆向考查．

例3已知曲线C:(5-m)x2+(m-2)y2=8(其中m∈R)．

1)若曲线C是焦点在x轴上的椭圆,求m的取值范围.

2)设m=4,曲线C与y轴的交点为A,B(其中点A位于点B的上方),直线y=kx+4与曲线C交于不同的点M,N,直线y=1与直线BM交于点G．求证:点A,G,N共线．

(2012年北京市数学高考理科试题第19题)

笔者发现,例1又是例3的另一种逆向考查.若将例1第2)小题改为“记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于点M,N,直线x=-1与直线MA1交于点P．求证:点A2,P,N共线”,则两道试题的考查方式就完全一致了,同类考查方式还可在教材中找到原型:

例4设抛物线y2=2px(其中p>0)的焦点为F,经过点F的直线交抛物线于点A,B,点C在抛物线的准线上,且BC∥x轴,求证:直线AC经过原点O．

(新苏教版《普通高中教科书·数学》(选择性必修第一册)第115页第11题)

此题中由于抛物线只有一个顶点,故可把抛物线的另一个顶点看成“无穷远点”,这就是题目中的条件“BC∥x轴”的含义．

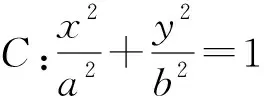
1)求椭圆C的方程.

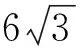
(2020年福建省高中数学竞赛预赛第12题)

不难发现,例1与例5除了背景不同外,第2)小题的考查方法几乎完全一致.可以证明,例5中的点T在一条定直线(即椭圆C的右准线)上．

对于此类问题的解法,笔者在文献[1]中进行了详细阐述,因此例1的解法本文不再赘述,下面对例1进行一般化探究．

3 试题探究

3.1 纵向探究

经探究发现,若将试题中的双曲线一般化,则点P仍在一条定直线上,于是有如下结论:

证明设直线MN的方程为x=ty+m,与双曲线C的方程联立,消去x,得

(b2t2-a2)y2+2b2tmy+b2m2-a2b2=0,

其中b2t2-a2≠0,且由Δ>0可得

b2t2-a2+m2>0．

设M(x1,y1),N(x2,y2),则

评注在结论1中若取m=-4,a=2,则可得例1中的点P在定直线x=-1上．

由极点与极线的理论可知,结论1中的点P所在直线恰好为点T(m,0)所对应的极线,此结论是巧合还是对一般的极点极线也成立呢?我们首先来看圆锥曲线极点与极线的定义:

定义1(几何定义)设P是不在圆锥曲线上的点,过点P引两条割线依次交圆锥曲线于4个点E,F,G,H,联结EH,FG交于点N,联结EG,FH交于点M,则直线MN为点P对应的极线．若P为圆锥曲线上的点,则过点P的切线即为极线．

定义2(代数定义)已知圆锥曲线Γ:Ax2+Cy2+2Dx+2Ey+F=0,则称点P(x0,y0)和直线l:Ax0x+Cy0y+D(x0+x)+E(y0+y)+F=0是圆锥曲线Γ的一对极点和极线．

由极点与极线的几何定义可快捷地得到结论1中点P所在的定直线:直线A1A2与MN交于点T(m,0),则由极点与极线的几何定义可知点P必在点T(m,0)所对应的极线上,再由极点与极线的代数定义可知点T(m,0)所对应的极线方程为

即

同样地,由极点与极线的两个定义,可以轻松得到如下结论:

3.2 横向探究

我们还可将结论1和结论2类比推广到椭圆和抛物线中:

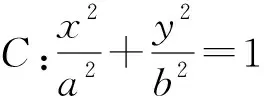
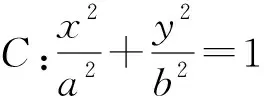
若把抛物线的另一个顶点看成“无穷远点”,则有如下结论5:

结论5已知抛物线C:y2=2px(其中p>0),点T(m,0)(其中m≠0)为x轴上任意一点,过点T的直线与抛物线C交于点M,N.若过点M且与x轴平行的直线与直线NO交于点P,则点P在定直线x=-m上．

结论6已知抛物线C:y2=2px(其中p>0),过点T(m,n)(点T不在C上)的直线与抛物线C交于点M,N,过点T的另一直线与C交于点A,B.若MA与NB交于点P,则点P在定直线ny=p(x+m)上．

3.3 逆向探究

受例2～4的启发,我们还可对上述结论进行逆向推广:

分析如图1,由极点与极线的几何定义可知直线MN与直线AB的交点在点P的极线上,只需证明点P的极线过点T(m,n).

图1

设P(x0,y0),则点P的极线方程为

故点T(m,n)的坐标满足直线

即点P的极线过点T(m,n)．而点P在直线l上,从而点P的极线必共点,且该点为直线l的极点,此点即为直线MN恒过的定点,故直线MN恒过点T(m,n)．

分析由极点与极线的几何定义可知直线MA与直线BN的交点在点T的极线l上,从而直线MA、直线BN及直线l共点,故点B,P,N共线．

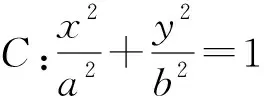
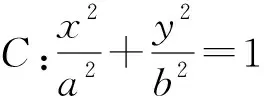
结论11已知抛物线C:y2=2px(其中p>0),点P为点T(m,n)(点T不在C上)的极线l:ny=p(x+m)上的动点,过点T的直线与C交于点A,B,直线PA,PB与C的另一个交点分别为点M,N,则直线MN恒过点T(m,n)．

结论12已知抛物线C:y2=2px(其中p>0),点T(m,n)(点T不在C上)关于抛物线C的极线为l:ny=p(x+m),过点T的直线与C交于点A,B,过点T的另一直线与C交于点M,N,直线MA交l于点P,则点B,P,N共线．

以上结论的证明过程略．

4 感悟反思

从历年的高考试题可以看出,很多高考圆锥曲线试题的命制都以极点、极线理论为指导．虽然极点与极线的知识不属于高考考查的内容,但是了解极点与极线的相关知识,能够帮助学生快速明确解题方向,能够培养学生探究问题和解决问题的能力．在例1中,如果学生了解极点与极线的相关知识,那么就很容易预见点P所在的定直线就是点(-4,0)所对应的极线,即直线x=-1,这为学生指明了解题的方向．另外,许多高考试题都可以从教材例题、习题以及往年的高考题中找到原型,因此在备考复习中,我们要做好以下几点:1)回归教材,立足于教材,对教材上的典型例题或习题加以概括、提高和延伸,以达到触类旁通的效果;2)重视往年高考题的导向作用,在临考前要让学生做一些历年高考中的经典试题,对这些试题的解法、命题背景、一般规律等进行总结归纳(如果学生考前对例2的解法、命题背景、一般规律等做过总结和归纳,那么在面对例1时相信不会有困难);3)在解题教学中,要用深度教学促进深度学习,力求达到“解一题,懂一法,会一类,通一片”的目标,要教会学生高位审视问题,深刻识别隐藏在题目背后的本质,这样才能在考试中“临危不乱”,才能做到“会当凌绝顶,一览众山小”．