大宽跨比大斜交角空心板桥受力分析
2023-09-21王晓平
王晓平,梁 晨
(1.山东交通职业学院,山东 潍坊;2.山东恒建工程检测有限公司,山东 潍坊)
引言
随着我国国民经济持续稳定的增长和综合国力的增强,带动了高等级公路及城市立体交通的全面发展,公路城市建设部门一改过去路线走向服从桥梁的思维模式,使得斜弯结构的桥梁在构造物中的比重越来越大。目前,斜交桥在高等级公路中所占比例已达到40%~50%,成为很重要的一种桥型。然而,目前交通部和部分省院颁布的空心板和装配式预制小箱通用图的斜交角度大部分在40°以下,对40°以上大斜交角的桥梁设计资料较少,特别是大宽跨比的空心板斜桥,几乎没有可供参考的资料。余钱华等[1]研究了小宽跨比小斜交角的空心板的跨中横向分布系数的计算方法,王荣霞等[2]对大宽跨比大斜交角的简支斜交T 梁桥跨中横向分布系数进行了研究,毛洪涛等[3]对大斜交角小箱梁的受力性能进行了研究分析,但这些结论是否适用于大宽跨比大斜交角的空心板桥上需要进一步验证。
1 工程实例简介
本文以潍坊某在役桥梁为基本算例,该桥跨径组合为6×13 m 普通钢筋混凝土简支空心板,斜交角为50°,用C40 混凝土,受力主筋为直径22 mm 的Ⅱ级钢筋(中板主筋17 根,边板主筋18 根);箍筋为直径8 mm 的Ⅰ级钢筋;桥面全宽25.5 m。中板及边板断面尺寸如图1 所示。
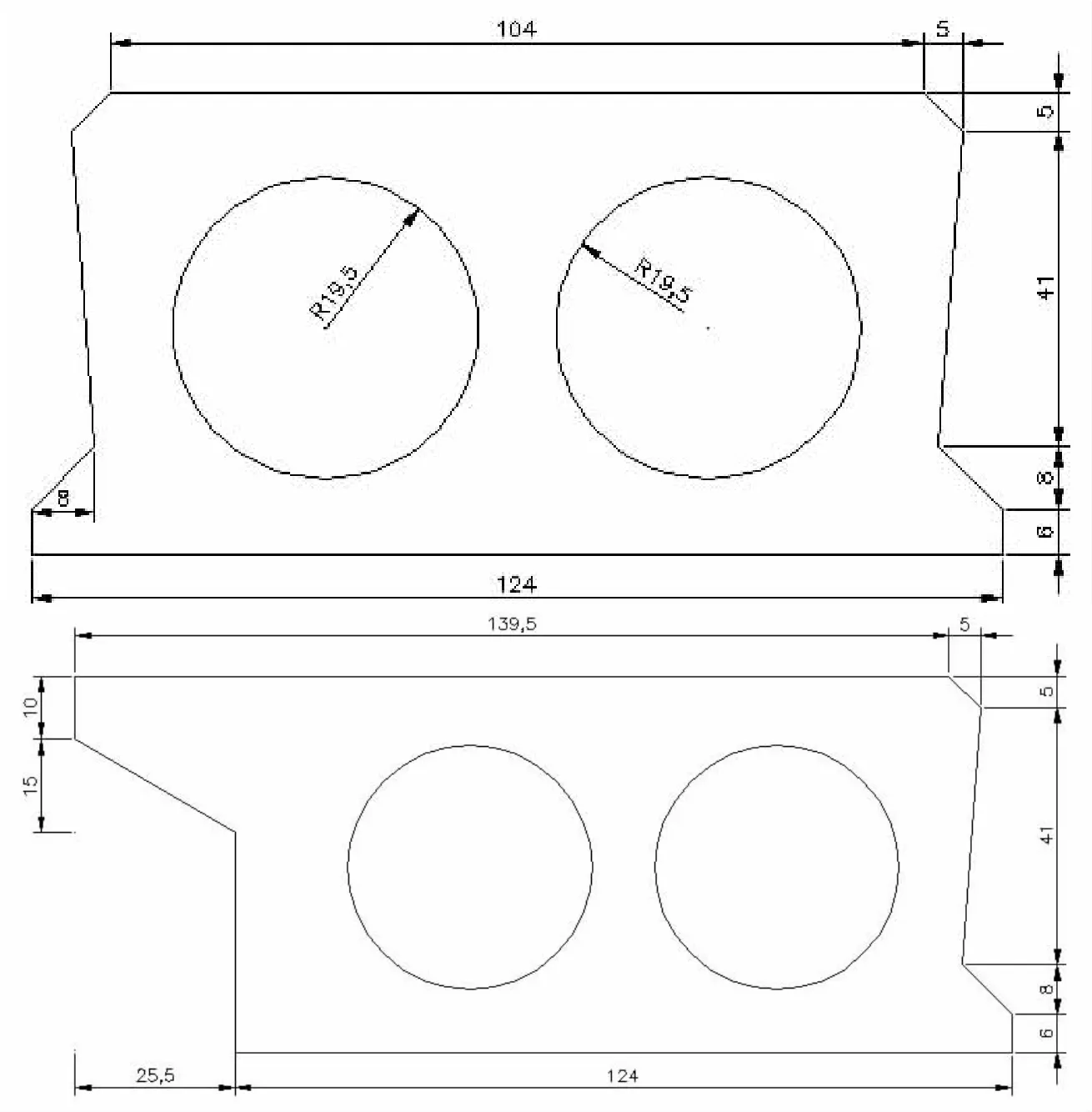
图1 中板及边板断面示意(单位:cm)
2 受力计算分析
对工程案例进行有限元模拟计算,并与荷载试验结果进行比较,以保证计算模型的准确性。以此为基础,对桥梁斜交角进行变参分析,讨论斜交角的变化对桥梁横向分布系数及内力的影响。荷载试验测点布置及有限元模型分别如图2 和图3 所示。

图3 工程实例模型
2.1 实桥验证
对工程实例桥梁进行荷载试验,加载工况如图2所示,将得到的位移数据与理论计算的位移数据进行比较,见表1,发现二者的变化规律大致相同,平均效验系数满足要求[4]。说明理论模型建立正确,可以以此为基础斜交桥的受力情况。
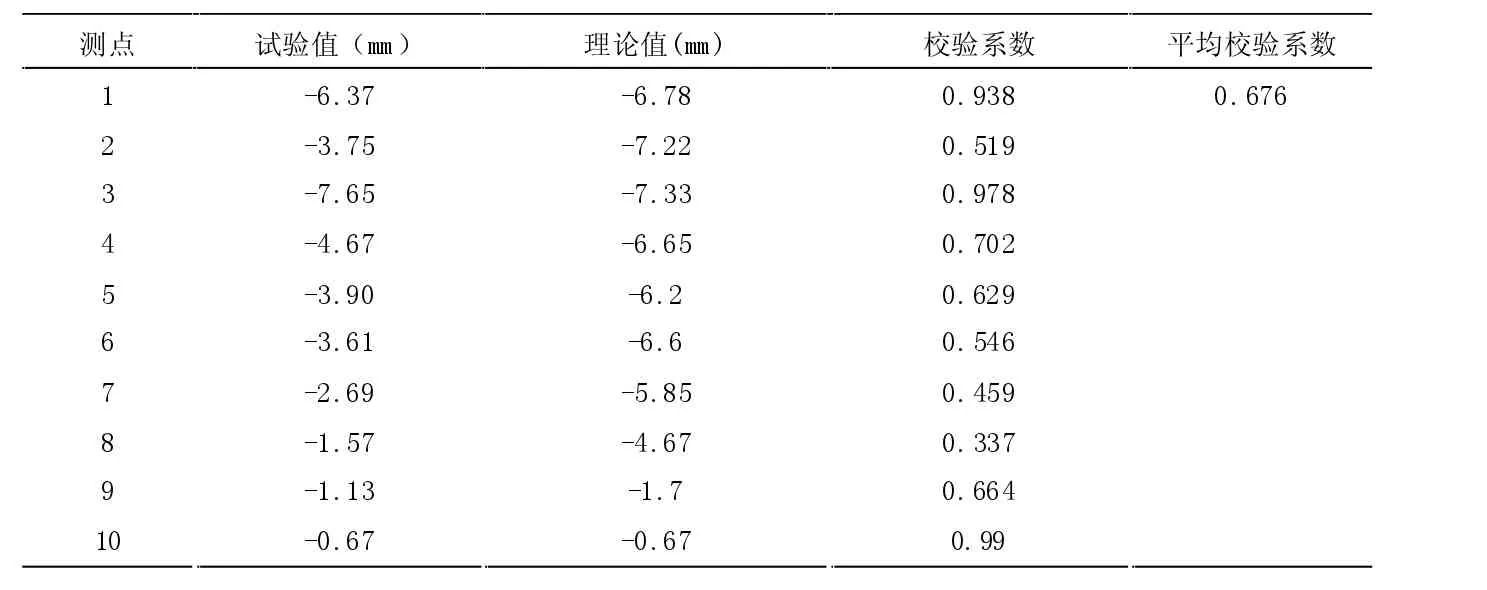
表1 试验位移与理论位移比较
2.2 横向分布系数分析
分别建立斜交角为0°到50°(间隔10°)的6 个宽桥模型,将各片梁的跨中挠度值代入公式(1),计算出各梁跨中横向分布系数[5],见表2。

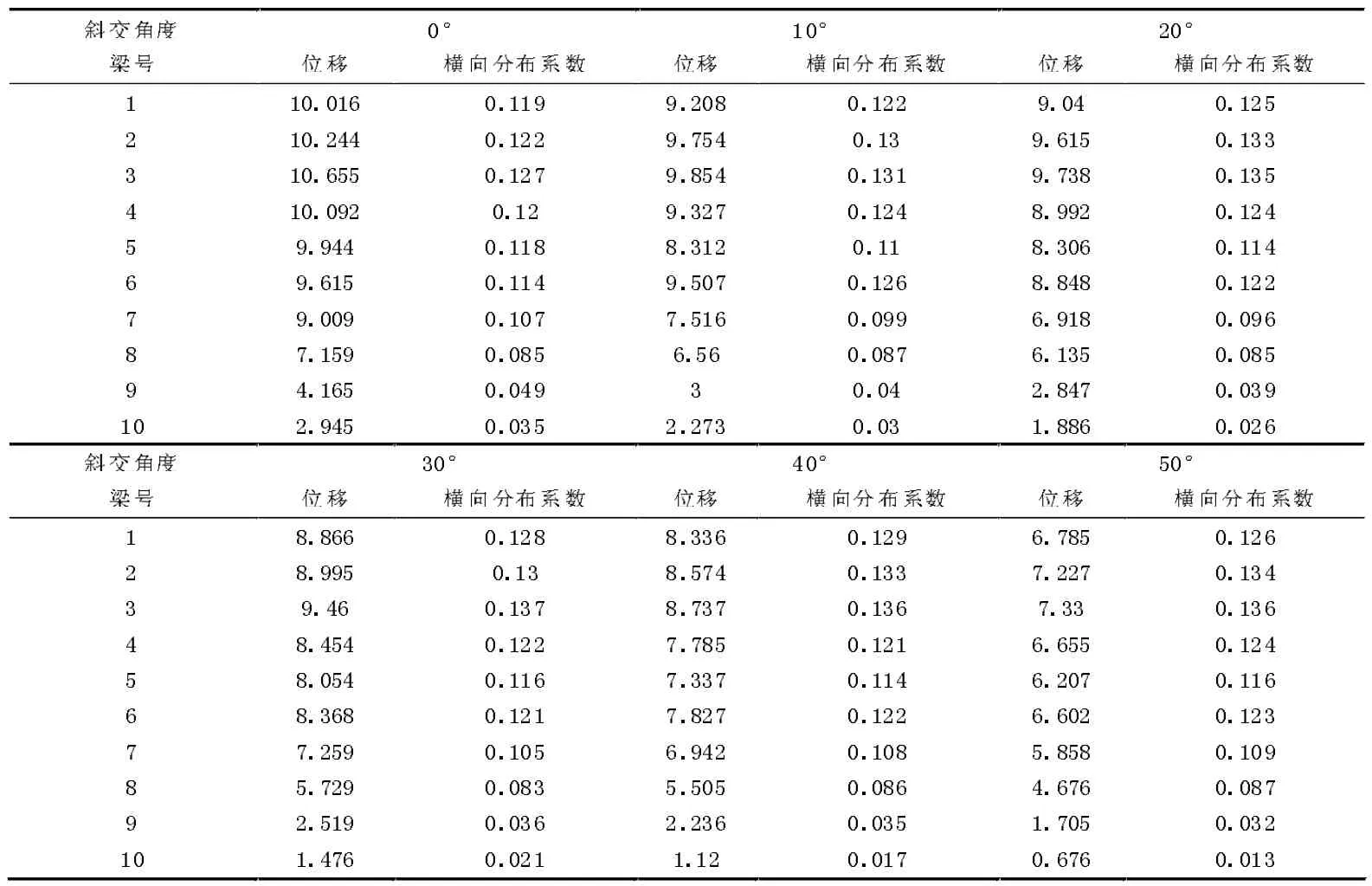
表2 不同斜度桥梁各主梁位移及横行分布系数
从表2 可以看出,随着斜交角的增大,各片主梁的竖向位移逐渐减小,说明斜交桥的刚度较正交桥更大,且从图4 可知,位移减小量随斜交角的增大而逐渐增大,当斜交角从40°到50°时,位移出现陡降段,说明当空心板斜交桥斜交角大于40°后,受力较正交桥变化很大。但是,随着斜交角的增大,主梁所受最大横向分布系数增加,最小横向分布系数减小,即各主梁的横向分布系数差值增大,说明同条件的斜交桥的横向连接性能比正交桥要弱,在桥梁养护过程中要更加留意铰缝等横向连接构件的质量。
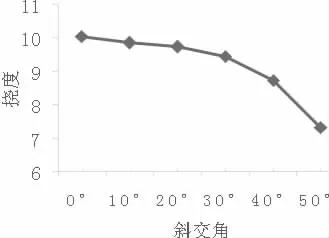
图4 最大位移随斜交角变化
2.3 主梁内力分析
从表3 可以看出,随着斜交角度增大主梁受到的弯矩逐渐减小,这也是前文中主梁挠度随斜交角增大而下降的主要原因。但是,随着斜交角的增大,主梁扭矩却在逐渐增加,说明斜交桥主梁之间扭矩的传递较正交桥不太顺畅,也进一步证明了斜交桥的横梁连接刚度较正交桥要弱。同时,也说明斜交桥的对抗弯钢筋的需求量下降,但对抗扭钢筋的需求量上升。

表3 不同斜交角下空心板梁的内力
对任何斜交角度的空心板桥,其中梁受弯矩均较边梁要小,但正交桥两者差值较小,随着斜交角增大,两者差值逐渐增大,说明斜交桥各主梁弯矩较正交桥分布更不均匀。但对某一固定斜交角的空心板梁,其外边梁和内边梁所受弯矩大致相等,说明空心板桥受力的对称性基本不受斜交角度改变的影响。然而,对固定斜交角度的空心板桥,其扭矩分布则为中梁大,边梁小,且随着斜交角度的增大,这个差值也逐渐增大。值得注意的是,各主梁所受弯矩和扭矩之和大致相当。
3 结论
(1) 随着斜交角增大,主梁最大横向分布系数增大,最小横向分布系数减小,随着斜交角增大,空心板桥的横向刚度下降,需要更加注意横向梁结构件的质量;
(2) 随着斜交角增大,主梁受到的弯矩减小,扭矩增大,挠度下降,说明斜交桥较正交桥可适当减少抗弯钢筋,但对抗扭钢筋的要求更高;
(3) 斜交角度越大,主梁弯矩减少越多,扭矩增大越多,挠度下降也越多,当斜交角大于40°后,各方面的受力性能较正交桥变化很大,需要重新设计截面配筋,以适应全新的受力状态。
