某新型执法装备高海情下滤波算法研究

张晓铎，周晓波，连 帅，高亚军

（郑州机电工程研究所，河南 郑州）

引言

中国海警是我国海上执法机构，其任务包括海洋巡航、执法监管、应急救援和海洋保护等，旨在维护国家主权和海洋利益，保障海上安全和秩序。

近年来，中国海警经历了高速发展，取得了显著成绩，在维护海洋权益、保护海洋环境和维护海上秩序等方面发挥了重要作用。通过加强装备建设、技术创新和协同合作，不断提升应对复杂海情的能力和水平，为海上执法和海洋权益保护作出积极贡献。

2016 年6 月19 日，央视报道海警21115 舰访问韩国，某新型执法装备工作画面曝光，日前《舰载武器》也已经刊登该新型执法装备列装海警执法船的照片。该型执法装备已经成为海警执法体系的重要组成。

海警船面对的海浪复杂情况是执法行动中常见的挑战之一。海浪的高度和周期的变化会对船舶的稳定性产生重要影响，大浪和短周期的海浪可能导致船舶剧烈晃动和颠簸，增加操作风险；海浪的方向和倾斜度也对船舶的稳定性和航行性能产生影响，增加操纵难度；倾斜的海浪可能导致船舶在航行过程中不稳定或产生滚动、颠簸等现象；海浪频谱的复杂性可能导致非线性效应，如波浪的相互作用和波浪的非线性传播，这些非线性特性可能导致海浪的形状和能量分布变化，给船舶带来额外的挑战，影响其稳定性和航行性能。

在高海情摇摆情况下，安装在甲板上的新型执法装备也会受到影响，如观测设备的稳定性降低，视野受限，难以准确捕捉目标信息和情报；设备的操作和维护困难，难以进行精确的操作。这些因素会导致目标瞄准和精确拒止变得困难，导致新型执法装备工作稳定性和精度受到影响。

滤波和预测算法研究对新型执法装备具有重要的工程指导意义。不仅能够提高装备的控制精度和稳定性，确保装备在复杂环境中的准确操作和目标追踪，还能够优化装备的性能和效率，提高工作效率和资源利用率。

1 滤波算法介绍

滑动窗口滤波通过保持最新一段时间内的观测数据并进行滤波处理获得对系统状态的估计。最小二乘滤波基于最小化估计误差平方和估计系统的状态或参数。卡尔曼滤波器基于系统的动态模型和传感器测量数据，可以对系统的状态进行迭代更新和预测，具有较强的鲁棒性。

文献[1] 提出了一种基于滑动窗口长短期记忆（LSTM）网络的船舶航迹预测方法，应用LSTM网络理论构建了基于滑动窗口LSTM网络的船舶航迹预测模型。文献[2]针对序列图像中非线性运动目标轨迹的预测问题, 提出了一种滑动窗口核岭回归运动目标轨迹预测算法。

文献[3]通过对航迹所关联若干点迹在一定时间、一定空间进行最小二乘拟合,然后进行航迹滤波。文献[4]利用最小二乘法对分成3 段的曲线进行船舶航行路线的拟合,建立拟合模型,提高了航迹模拟的精准性。

文献[5]对扩展卡尔曼滤波器进行改进，提出了自适应变噪声数学模型，并利用非线性互补滤波器对实验结果进行并行数据融合。文献[6]设计了一种融合奇异值分解（SVD）和无迹卡尔曼滤波（UKF）的非线性动力定位状态估计算法。文献[7]考虑了系统噪声和量测噪声,提出了一种基于扩展卡尔曼滤波器和滑模控制结合的复合控制算法。文献[8]应用自适应鲁棒UKF(ARUKF)算法和遗传-UKF(GUKF)算法,建立了基于SQP 优化的改进UKF算法(SUKF),既保证了对准精度，又提高了对准速度。

综上所述，滑动窗口滤波、最小二乘滤波和卡尔曼滤波在新型执法装备算法应用上具有各自的应用必要性。滑动窗口滤波适用于实时性要求较高、计算复杂度要求较低的场景。最小二乘滤波通过优化性能和适应非线性系统，可提供高精度的状态估计和目标跟踪。卡尔曼滤波器基于系统建模和鲁棒性适应性，可以实现对目标的稳定跟踪，确保拒止控制的精度。

2 滤波算法设计

2.1 最小二乘滤波

匀速直线运动最小二乘滤波公式如下：

2.2 容积卡尔曼滤波（CKF）

容积卡尔曼滤波（CKF）算法处理流程如下:

2.2.1 时间更新

2.3 无迹卡尔曼滤波UKF

无迹卡尔曼滤波(UKF)算法的运算流程如下：

2.3.1 状态和协方差初始化

2.3.2 计算采样点及其对应权值

3 滤波算法仿真分析

3.1 摇摆条件下匀速目标跟踪预测

假设目标航路捷径50 m、高度20 m、起点在左侧500 m，目标以300 m/s 的速度向右匀速直线运动。舰船横摇幅值22.5°、周期5 s，纵摇幅值7.5°、周期5 s，摇摆值中加入均方根为0.01°的噪声。分别对滑动CA、滑动CV、最小二乘CA、最小二乘CA、最小二乘CAA、卡尔曼CV、卡尔曼CA、UKFCV、UKFCA 和CKFCA 航迹预测算法进行了仿真分析。

各种滤波效果统计如表1 所示。

表1 摇摆条件下匀速目标跟踪预测效果统计

在此种模型下，预测效果从好到坏的排序为：最小二乘CA、滑动窗口CV、最小二乘CAA、最小二乘CV、滑动窗口CA、UKFCA、UKFCV、标准卡尔曼CA、标准卡尔曼CV和CKFCA。图1 为最小二乘CA 和CKFCA 预测误差曲线对比。

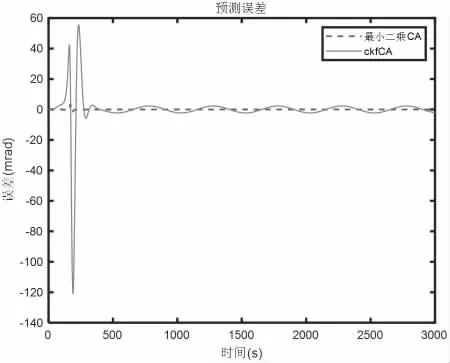
图1 摇摆条件下匀速目标跟踪预测误差对比曲线

3.2 噪声对滤波效果的影响

假设目标以300 m/s 的速度运动，分别加入2 m、5 m 和10 m 的噪声到理论值中，分别进行仿真，不同的噪声对滤波效果的影响见表2。

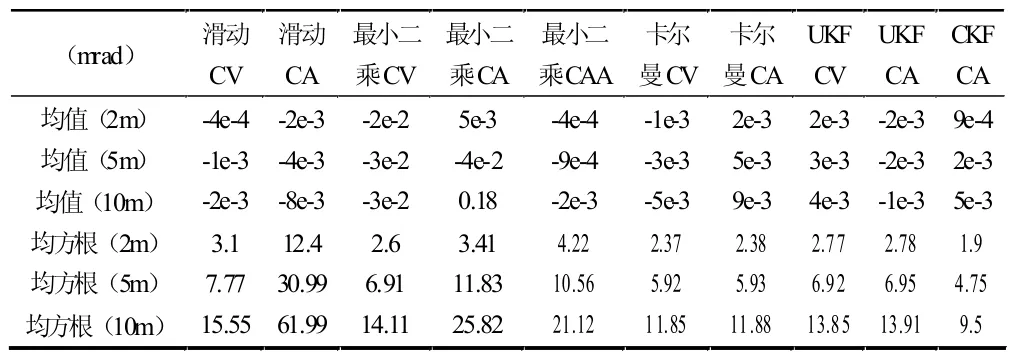
表2 匀速运动模型下噪声对滤波效果的影响分析

由表2 可以看出，在噪声比较大的匀速运动模型中，卡尔曼及其变种的滤波方法能取得较好的效果，并且随着噪声的增大，这种效果越来越明显。其中，无迹卡尔曼滤波（UKF）表现得尤为突出，基本上是约等于噪声的均方根。

假设目标运动是以振幅15°、周期4 s 的正弦方式运动，分别加入0.01°、0.02°和0.05°的噪声到理论值中，分别进行仿真，不同的噪声对滤波效果的影响见表3。

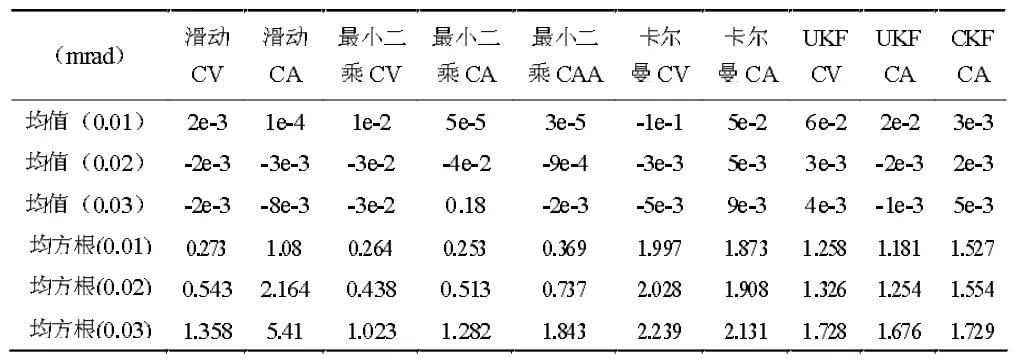
表3 正弦运动模型下噪声对滤波效果的影响分析

由表3 可以看出，在对含噪声的正弦模型进行滤波预测，CV 模型的最小二乘滤波能得到较好的效果，卡尔曼及其变种的滤波方法未能取得较好的效果。

由以上仿真分析可知，对于摇摆条件下的匀速直线模型，最小二乘CA 滤波效果最好；对于采样周期一定的有噪声的线性模型，特别是噪声比较大的匀速直线运动模型，无迹卡尔曼滤波（UKF）和最小二乘CV 滤波算法能取得不错的效果；对于有噪声的正弦运动模型，最小二乘CV、CA滤波算法能取得较好的效果。

4 结论

针对某新型执法装备在高海情下稳定跟踪的工作需求，本文建立了目标匀速、匀加速和正弦运动模型，基于滑动窗口、最小二乘和卡尔曼滤波开展了滤波算法研究，对比了噪声情况下各算法的仿真对比，仿真结果表明针对噪声比较大的匀速直线运动模型，容积卡尔曼滤波和最小二乘CV滤波算法效果较好，而对于有噪声的正弦运动模型，最小二乘CV、CA和滑动窗口CV 滤波算法效果较好。本文开展的滤波算法研究对某新型执法装备算法优化具有工程指导意义。