特高压输电线路拉线塔拉线- 金具系统的风载荷计算及疲劳特性分析

黄青松，王晓兵，王东阳，孙俊龙

（1.平高集团有限公司，河南 平顶山；2.河南省建设科技和人才发展中心，河南 郑州)

拉线塔具有柱身断面小、施工周期短、稳定性好等一系列优势，在高压和特高压输电线路中被广泛应用。随着拉线塔使用年限的增加，由于材料自身老化以及多次重复荷载作用的影响，材料的屈服极限降低，容易出现疲劳破坏，严重时还有可能导致拉线塔的倒塌。其中，拉线塔上的拉线- 金具系统由于受力特殊，是疲劳分析的重点对象。分析拉线- 金具系统的疲劳特性，能够为今后特高压输电线路拉线塔的结构优化与日常维护提供参考，对保障特高压输电线路安全有一定帮助。

1 拉线- 金具系统的风载荷计算

位于野外空旷地带的拉线塔，在风力作用下会产生风振疲劳损伤，并且风速的大小与疲劳损伤的程度密切相关。在三维空间中，各个方向上风的出现频率和强度均表现出明显差异；在低风速时，风速方向的分布较为离散。为了更加准确地描述风载荷对拉线-金具系统的影响，本文运用概率密度函数描述风的特征，该函数可表示为：

式中，P、Q 为描述任意方向上不同大小风速出现概率的可变参数，v 表示平均风速。各个方向上的P 值、Q值以及出现风的百分比如表1 所示。

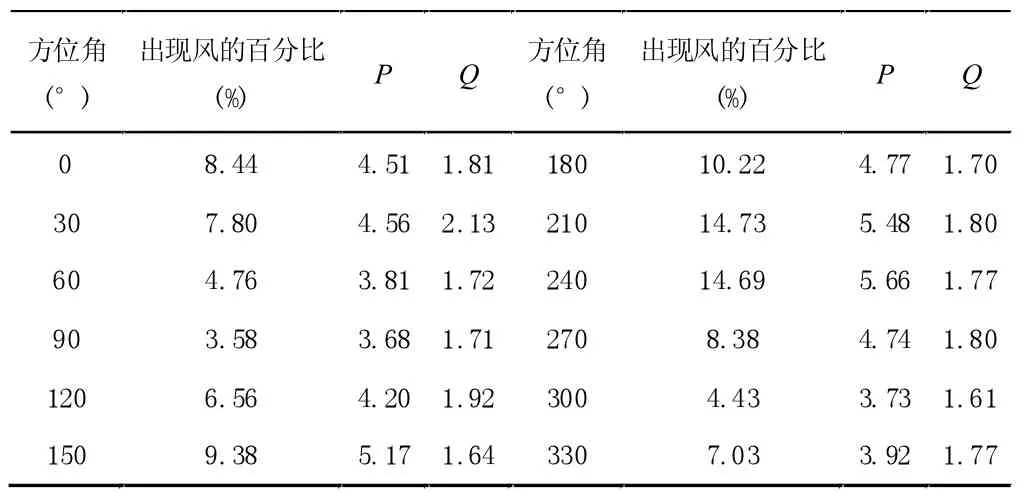
表1 风在各个方向上的出现频率

将表1 中的P 值、Q 值代入到式（1）中，可以求得任意方向上风速的分布概率。这里以240°方向为例，各个风速的分布概率如图1 所示。

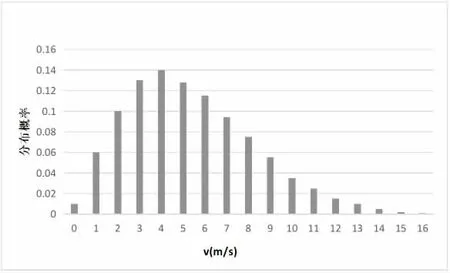
图1 某地240°方向上各平均风的概率分布

结合图1 可知，该地区240°方向上，分布概率最高的风速为4 m/s；其中，10 m/s 以上的高风速分布概率仅为0.093，占比不足10%，说明该地区大风出现概率较低。

2 疲劳破坏区应力幅统计

2.1 单柱拉线塔的模型构建

结合以往的拉线塔维修经验以及查阅相关资料，可以得出“拉线- 金具系统疲劳断裂主要分布在应力集中区”的结论。在特高压输电线路的拉线- 金具系统中，金具通过液压压接的方式将拉线与拉线塔连接起来。为了保证两者连接牢固，需要在压接管口位置施加一个较大的作用力，由此产生了应力集中现象。在拉线- 金具系统的疲劳特性分析中，将金具与拉线接触的压接管口位置作为疲劳破坏区进行重点分析[1]。

本文参照某地800KV 直流输电线路中的单柱拉线塔，使用ANSYS 软件构建了拉线塔仿真模型，导线型号为JL/G3A-1000/45，截面积1 036 mm2；地线型号为LBGJ-150-20AC，截面积为150 m2，参数设置如表2 所示。

表2 单柱拉线塔工程条件

仿真模型搭建完成后，在拉线塔上施加一个初始预应力，随后改变风载荷条件，模拟拉线塔在不同风向、不同风速下的风振响应，并绘制10 min 内拉线轴向应力时程曲线。从该曲线中，提取出疲劳破坏区的应力时程曲线，利用“雨流计数法”求出拉线- 金具系统疲劳区的应力幅。

2.2 拉线- 金具疲劳区应力幅的统计方法

目前计算拉线- 金具系统的累计疲劳损失，常用的做法是将应力幅的幅值进行细分，分别计算出每个部分应力幅值的出现次数，最后求和。在幅值统计过程中，需要运用到循环计数法、雨流计数法等方法。本文选用“雨流计数法”，其原理是将“应力- 时间历程”数据记录旋转90°，使时间坐标轴垂直线下，让应力值像雨水一样自上而下流动。具体实现过程为：

步骤1：将“应力- 时间历程”曲线以顺时针方向转动90°，规定垂直向下的轴线为时间轴，水平向右的轴线为应力轴。

步骤2：任意选定一个峰值或谷值开始计数。假设从峰值开始计数，如果一个从峰值开始的流动到达临近谷值时，判断下一个峰值与开始峰值的大小。如果下一个峰值较大，则流动停止；反之，如果下一个峰值较小，则继续流动。

步骤3：流动结束后，流动轨迹在应力轴上的投影长度，即为该半循环的幅值[2]。

使用雨流计数法，统计10 min 内沿120°方向平均风速为10 m/s 时，各应力水平结构实际循环次数百分比，结果表明：应力幅为1 MPa 的循环次数百分比最高，达到了44.7%；随着应力幅的增加，循环次数百分比逐步下降，在应力幅超过10 MPa 后，循环次数百分比降低至1%以下。

2.3 拉线- 金具疲劳区应力幅的计算结果

现有的研究表明，在应力循环方式不同的情况下，只要保证应力幅一致，那么应力对构件及其连接件的疲劳效应是相同的。由此可见，要想延长拉线-金具系统的疲劳寿命，必须要将应力幅作为重点研究对象。参考《钢结构设计规范》（GB50017-2017）中的有关规定，对于焊接结构，若应力幅为常量时，可采取下式进行疲劳计算：

式中，Δρ 表示应力幅。对于焊接结构，取应力循环中最大拉应力与最小拉应力之差；[Δρ] 表示常幅疲劳的容许应力幅，可通过下式求得：

式（3）中，n 表示应力循环次数；k 和λ 为系数，由拉线- 金具系统中构件和连接类别决定，具体取值见表3。

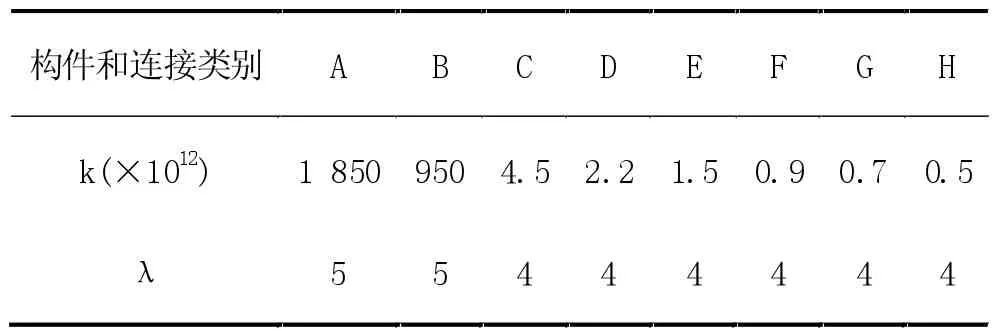
表3 系数k 和λ 的取值表

参考《钢结构设计规范》（GB50017-2017）中的有关规定构件和连接类别总计8 种，以字母A～H 表示[3]。经过对比，本文研究的拉线- 金具系统与第7 种构件和连接类别（即表3 中G 栏）最为接近，因此在计算中k 值为0.7×1012，λ 值为4。将数据带入式（3）后可以求得常应力幅下的“应力幅- 循环次数（S-N）”曲线，如图2 所示。

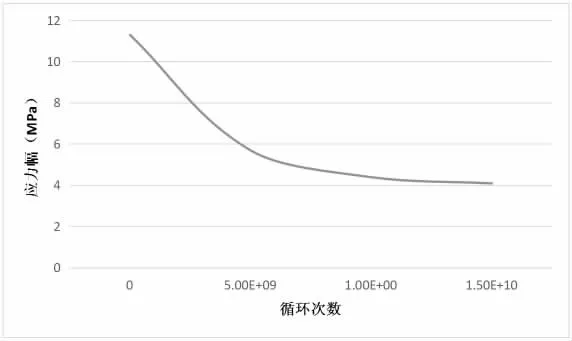
图2 材料S-N 曲线

上文讨论了应力幅为常量情况下拉线- 金具系统的疲劳计算方法。而实际中，由于材料自身特性、外界风力变化等多种因素的影响，应力幅通常为变量（变幅疲劳）。对于变幅疲劳情况，可采用线性累积损伤公式求解拉线- 金具系统的疲劳，计算公式为：

式（4）中，Δi表示应力幅为Δρi破坏时对应的循环次数为ni时的累积损伤；Ni表示应力幅为Δρi，并且出现疲劳破坏时对应的循环次数，即疲劳寿命。将式（3）代入到式（4）中，可以得到：

当Δ 为1 时，结构发生疲劳破坏。

3 拉线- 金具结构的疲劳寿命预测

由于风载荷的随机性，拉线塔结构的响应也表现出随机特点。为了准确估算出变幅应力下拉线塔拉线- 金具结构的疲劳寿命，可使用Miner 线性累积疲劳损伤理论进行计算[4]。公式为：

式（6）中，任意选择3 组点（假设为n1N1、n2N2、n3N3），以N 为横坐标，以n 为纵坐标，在平面坐标系上标记出3个点的位置，然后用直线将3 个点连接起来，即可得到“S-N”曲线，如图3 所示。

图3 Miner 理论示意图

由图3 可知，在该坐标系中，任意一个应力水平Δρi，对应的破坏循环次数为Ni，则Ni的表达式为：

式中，ΔρF表示变幅疲劳极限应力幅，NF表示对应ΔρF的循环次数，λ 表示倾斜度。为了便于分析，本文通过一个等效的应力水平与破坏循环次数，代替原来多种应力水平下的实际循环次数[5]。则等效破坏循环次数（Ne）可表示为：

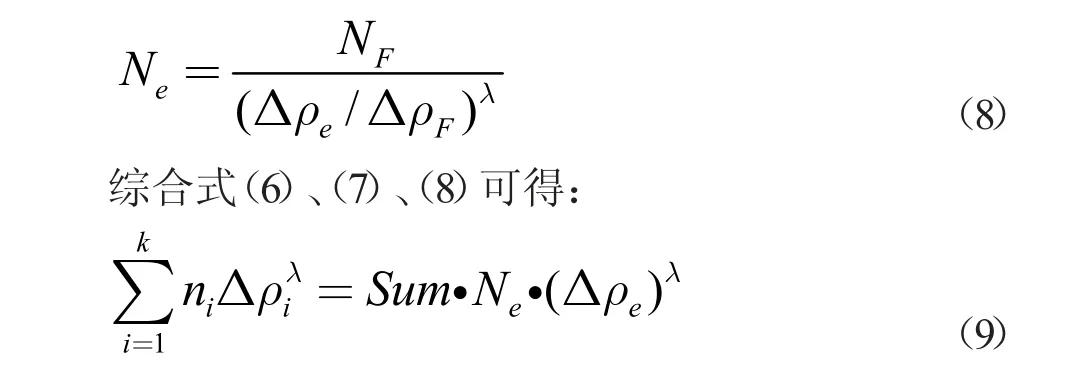
计算后式（9）左侧为9.03×1010，Sum 为0.14。令Ne取107，将各项数据带入式（9）后，求得Δρe的值为40.12 N/mm2。在此基础上，利用上文给出的式（3），计算构件疲劳破坏循环次数。将式（3）两边进行对数处理，计算公式变为：

求得lgn=7，相应的n=107，即构件疲劳循环次数（疲劳寿命）为107次。

在估算出拉线塔拉线- 金具系统的使用寿命后，能够为后续的检修维护工作提供参考。工作人员可以在拉线- 金具系统即将达到疲劳寿命时，对其进行更换，从而保证了拉线塔拉线- 金具系统的可靠运行，对保证特高压输电线路的运行安全起到了积极帮助。

4 结论

在特高压输电线路中，相比于常见的自立塔，拉线塔表现出结构简单、安装方便、受力性能好等优势，尤其是在地形复杂的山区有着广泛使用。拉线塔的拉线- 金具系统在长期受到风载荷的影响后，容易出现不同程度的疲劳损坏，如果不能及时处理可能会出现拉线断裂等问题，不仅影响特高压输电线路的正常供电，而且还会带来严重的安全隐患。采用雨流计数法求得疲劳破坏区应力幅循环次数，在此基础上基于Miner 线性累积疲劳损伤理论，估算出拉线- 金具系统的疲劳寿命，让拉线塔拉线- 金具系统的疲劳损伤情况得以量化表示，为检修维护工作的开展提供了依据，切实保证了拉线塔的结构安全。