GV-平坦模

张晓磊

(山东理工大学 数学与统计学院，山东 淄博 255000)

0 引言

本文所有的环均指有单位元的交换环.众所周知，平坦模类作为经典同调代数的三大模类之一，对同调代数与环论的发展起着非常重要的作用，例如，利用平坦模类构造模的经典平坦维数和环的弱总体维数；平坦模类也可以刻画von Neumann正则环、 Prüfer整环和凝聚环等经典环类[1].近来，广义平坦模得到了越来越多学者的关注.2010年，Xiang[2]引入Max-平坦模并研究了其盖包理论；2013年，Tang[3]引入强Max-平坦模并研究了模的强Max-平坦维数.1993年，Enochs等[4]引入并研究了一般环上的Gorenstein平坦模，进而完备了一般环上的Gorenstein同调代数理论.

星型算子，例如v-算子和t-算子，在经典整环的推广研究中起着关键作用，如Mori整环既可以看成v-版本的诺特整环，又可以看成t-版本的诺特整环.为了研究强Mori整环，1997年，Wang等[5]引进整环上的w-算子，并且定义了w-模等相关概念.2010年，Yin等[6]将文献[5]的工作扩展到一般交换环上.自此之后，交换环上w-算子的模理论成为研究交换环论的一种重要方法.2014 年，Kim等[7]引入w-平坦模，并给出了w-内射模的若干等价刻画.随后，Wang等[8]证明了R是von Neumann正则环当且仅当任意R-模都是w-平坦模；Wang等[9]利用w-平坦模引进了环的w-弱总体维数，证明了PvMD恰好是w-弱总体维数至多为1的整环.

本文利用w-算子从另一个角度推广平坦模，得到了GV-平坦模.我们研究了GV-平坦模的一般性质和盖包性质，特别地，利用GV-平坦模刻画了DW-环、von Neumann正则环和GV-凝聚环.

R-同态f:A→B称为 w-单同态(w-满同态,w-同构)，如果对任意m∈w-Max(R)，都有fm:Am→Bm是单同态(满同态,同构).序列A→B→C称为w-正合列，如果对任意m∈w-Max(R),Am→Bm→Cm是正合列.

设M是R-模.若存在有限生成自由F和一个w-满同态g:F→M，则称M为有限型的；若存在w-正合序列F1→F0→M→0，其中F0和F1是有限生成自由模，则称M为有限表现型的.

1 GV-平坦模

定理1设F是R-模，则下列结论等价：

(1)F是GV-平坦模；

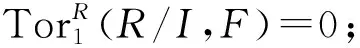
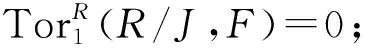
(4)对任意弱GV-理想I，乘法同态iI:I⊗RF→IF是同构;

(5)对任意GV-理想J，乘法同态iJ:J⊗RF→IF是同构;

(6)设E是R-模的内射余生成子，则HomR(F,E)是GV-内射模;

(7)对任意内射模E，HomR(F,E)是GV-内射模.

可得：对任意弱GV-理想I，有

从而HomR(F,E)是GV-内射模.

即可得证.

令J=Ra1+…+Ran+L，则J是GV-理想(文献[1]命题6.1.9(2)).考虑交换图

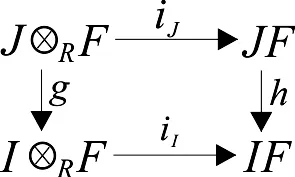
设M是R-模.若对任何w-单同态f:A→B,1M⊗Rf:M⊗RA→M⊗RB仍是w-单同态，则称M为w-平坦模[7].R-模M是w-平坦模当且仅当对任意m∈w-Max(R)，Mm是平坦Rm-模[1].关于w-平坦模的更多介绍可参见文献[12].显然，GV-挠模和平坦模都是w-平坦模.

下面例子说明GV-挠模不一定是GV-平坦模.

例1设R=k[x1,x2]是域K上的二元多项式环.令J=x1,x2，则根据文献[1]例7.6.1可得J是GV-理想，从而R/J是GV-挠模.因为J不是幂等理想，所以从而R/J不是GV-平坦模.

众所周知，环R是DW-环当且仅当R的GV-理想只有R本身.下面利用GV-平坦模刻画DW-环.

定理2设R是环，则下列结论等价：

(1)R是DW-环；

(2)任意R-模都是GV-平坦模；

(3)GV-平坦R-模的子模是GV-平坦模；

(4)平坦R-模的子模是GV-平坦模；

(5)任意有限生成理想都是GV-平坦理想.

根据文献[8]定理 4.4可得，R是von Neumann正则环当且仅当任意R-模都是w-平坦模，从而存在GV-平坦模M不是w-平坦模的环.

引理1设p是R的素w-理想，M是R-模，则Mp是GV-平坦R-模.

显然，任意平坦模都是GV-平坦模.下面我们刻画GV-平坦模都是平坦模的环.

引理2设R是环，则下列结论等价：

(1)R是von Neumann正则环；

(2)任意GV-平坦R-模都是平坦模.

智能变电站中，站控层相当于整个电网的控制层，其组成由主计算机、路由器以及一些人机交互的设备等。站控层的设置目的是对变电站进行检测以及控制，在发现险情时及时报警的装置，当变电站发生技术上的问题时，主计算机和这些人机交互的设备会在第一时间记录下电能交换时产生的异常，并及时作出相应的处理，反馈给控制中心，给上一级的变电站提供解决问题和应对措施的信息。

2 GV-平坦模类的盖包性质

一个R-模类R称为预盖类，如果对任意R-模M，存在一个同态f:F(M)→M，其中F(M)∈R使得对任意F∈R,g:F→M必然经过f分解.此外，如果使分解f=fh成立的h只有同构，则称R为盖类.对偶地，可以定义预包类和包类.

设R是R-模类.记

文献[15]证明了w-平坦模类是盖类，下面结果说明GV-平坦模类也是盖类.

若环R的任意有限型理想是有限表现型的，则称环R为w-凝聚环[17].文献[18,19]证明了：环R是w-凝聚环当且仅当任意平坦R-模的直积是w-平坦模，当且仅当R的任意直积是w-平坦模.为了研究GV-平坦模类的直积性质和(预)包性质，下面引入GV-凝聚环.

定义2设R是环，若任意GV-理想都是有限表现的，则称R为GV-凝聚环.

显然，DW-环、凝聚环都是GV-凝聚环.为了给出一个环是GV-凝聚环但不是w-凝聚环的例子，我们回顾环的理想化构造[20].

设R是环，M是R-模，令R(+)M作为R-模同构于R⊕M.定义

( i )(r,m)+(s,n)=(r+s,m+n);

(ii)(r,m)(s,n)=(rs,sm+rn).

则R(+)M成为有单位元R(+)M的交换环.

下面给出w-凝聚环不是GV-凝聚环的例子.

例4设R是非凝聚的GCD整环[1]，则存在有限生成理想I=x1,…,xn不是有限表现的(其中xi≠0,i=1,…,n).令d=gcd(x1,…,xn)为x1,…,xn的最大公因子，则存在有限生成理想J使得I=dJ.根据文献[1]例7.6.1可得，J是GV-理想.但由于J≅I，J不是有限表现的，故R不是GV-凝聚环.因为R是GCD整环，所以R是w-凝聚环.

定理4对于环R，下列结论等价：

(1)R是GV-凝聚环；

(2)GV-平坦模的直积是GV-平坦模；

(3)平坦模的直积是GV-平坦模；

(4)R的直积是GV-平坦模；

(5)对于任意GV-内射模N及内射模E，都有HomR(N,E)是GV-平坦模;

(6)若E是内射余生成子，则对于任意GV-内射模N都有HomR(N,E)是GV-平坦模.

(7)对任意GV-平坦模M及内射模E1,E2，都有HomR(HomR(M,E1),E2)是GV-平坦模.

(8)若E1,E2是内射余生成子，则对任意GV-平坦模E1和E2都有HomR(HomR(M,E1),E2)是GV-平坦模.

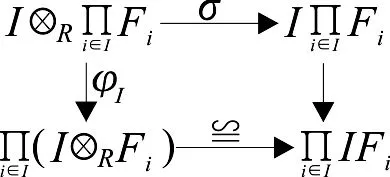
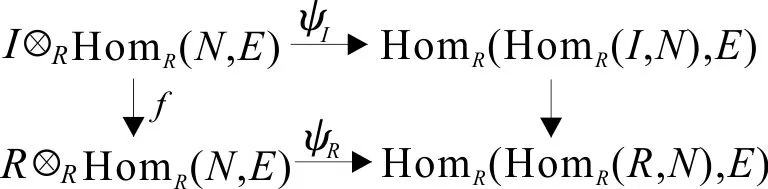
由(6)可得f是单态射.故ψI是单态射，从而由文献[21]命题8.14(1)可得，I是R-Mittag-Leffler模.又因为I是有限生成理想，所以根据文献[14]定理2可得，I是有限表现理想.】

定理5设R是环，则R是GV-凝聚环当且仅当GV-平坦模类FGV是预包类.

推论1设环R是GV-凝聚环，GV-平坦模类FGV关于反向极限封闭，所以FGV是包类.

证明由定理 5可得GV-平坦模类是预包类，从而由文献[22]推论6.3.5可得FGV是包类.】

推论2设R是环，则下列结论等价：

(1)R是DW-环；

(2)任意R-模都有满的GV-平坦包；

(3)任意R-模都有满的GV-平坦预包.