拓扑图形密码导出文本密码的一种技术

2023-09-19孙宜蓉

西北师范大学学报（自然科学版） 2023年5期

孙宜蓉，姚兵*

(西北师范大学数学与统计学院，甘肃兰州 730070)

0 引言

随着互联网的迅猛发展和网民数量的日益增多，密码认证成为人们在互联网应用和现实生活中常用的安全手段.图形密码是一种全新的身份认证技术.与传统的文本密码不同，图形密码使用图形作为认证媒介，通过用户对图形的点击、识别、重现，或者用户与图形系统的互动进行认证.然而，图形密码需要占用大量计算机的存储单元，造成运行缓慢；并且用户不能自己随意更换图片，或者自己设计图形密码.

近来，Wang等[1-2]提出了一种新的图形密码，叫做拓扑图形密码，它与现存的图形密码(比如二维码)有所不同，是通过代数矩阵存储在计算机中的.拓扑图形密码的一个优点是它可以通过拓扑图产生一个很长的文本密码.文献[3]介绍了从拓扑图形密码生成文本密码的一些方法，这些方法是基于图的拓扑结构和图标号产生的，其中一些方法还可以转换成多项式算法.文献[3]还介绍了产生文本密码D(a)的“路-邻居”方法，此方法对以毛毛虫树为拓扑结构的图形密码极为有效.但是，没有给出具体的算法来得到奇优美毛毛虫树.本文给出一个快速的多项式算法来解决这个问题，并给出顶点剖分方法下的一个奇优美毛毛虫树算法.

文中有关图论的标准术语和记号可参见文献[4,5]，且所提及的图均为有限、无向、简单图.为叙述简洁，当m和n均为整数且0≤m

若图G中任两个顶点x,y之间都能用唯一的一条路P(x,y)=xu1u2…umy连接，则称图G是一棵树，树中的一度顶点称为树的叶子.如果把树中的所有叶子都删掉后，仅剩路P，则称树为毛毛虫树；如果把树中的所有叶子都删掉后，仅剩毛毛虫树，则称树为龙虾树；若图G中有p个顶点q条边，则称图G是(p,q)-图.

1 毛毛虫树图形密码的两个算法

1.1 奇优美毛毛虫树算法

设毛毛虫树H中的一条路为P=u1u2…un，记每个顶点ui的叶子集合为L(ui)={vi,j:j∈[1,mi]}，其中mi是整数，mi≥0且i∈[1,n]，则V(H)=V(P)∪L(u1)∪L(u2)∪…∪L(un).毛毛虫树的结构如图1所示.

图1 毛毛虫树

由于图H是二部图，所以它的顶点集二部划分(X,Y)为：当n为偶数时，

当n为奇数时，

奇优美毛毛毛虫树算法

初始化.令h是毛毛虫树H的一个标号.先对X中顶点进行标号.令

步骤1.n为偶数.当2≤i≤n/2时，令

其中j∈[1,m2i].再对Y中顶点进行标号.因为

所以令

它是奇数.再令

其中j∈[1,mn-1].则h(un)-h(vn,mn)=1,h(un-2)=h(vn-1,mn-1)+2,h(vn-3,j)=h(un-2)+2j，其中j∈[1,mn-3].

当1≤i≤n/2-1时，令

其中j∈[1,mn-(2i+1)].

由以上标号可得

所以hmax(X)

现计算边标号：当j∈[1,mn]时，有

因为当j=mn时h(unvn,mn)=1，当j=1时h(unvn,1)=2mn-1，所以，当j∈[1,mn]时，h(unvn,j)∈[1,2mn-1]o，且

当i∈[1,n-1]o时，有

又当i∈[2,n-2]e时，有

综上所述，当i∈[1,n-1]时，有

当i∈[1,n-1]o时，有

所以

又当i∈[2,n-1]e时，有

所以

综上所述，当i∈[1,n-1]时，有

以上证明可以断言

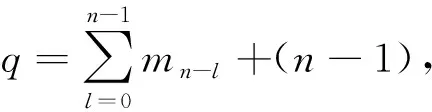
步骤2.n为奇数.令n=2p+1.当i∈[1,p]时，令

它是偶数；当i∈[1,p-1]时，令

其中j∈[1,m2i+2].再对Y中顶点进行标号，令

当i∈[1,p]时，有

其中j∈[1,m2p-(2i-1)]；

当i∈[1,p-1]时，有

由以上标号可得

所以hmax(X)

现计算边标号：

因为当j=1时h(u2p+1v2p+1,1)=1，当j=m2p+1时h(u2p+1v2p+1,m2p+1)=2m2p+1-1.所以当j∈[1,m2p+1]时有h(u2p+1v2p+1,j)∈[1,2m2p+1-1]o，且

同理可得h(u2pv2p,j)∈[2m2p+1+3,2m2p+1+2m2p+1]o.

当i∈[1,2p-1]o时，有

又当i∈[2,2p-2]e时，有

综上所述，当i∈[1,2p-1]时，有

当i∈[1,2p-1]o时，有

所以

又当i∈[2,2p-2]e时，有

所以

综上所述，当i∈[1,2p-1]时，有

以上证明可以断言，

1.2 奇优美毛毛虫树剖分算法

本节算法与上面算法类似，这里仅通过实例(图2)解释奇优美毛毛虫树剖分算法.

图2 奇优美毛毛虫树剖分算法

2 总结和问题

本文给出了一个多项式算法来产生毛毛虫树的奇优美标号.文献[3]给出了产生文本密码的技术，利用本文的标号技术可以很容易地产生文本密码，利用这个具体的标号可以产生随机的奇优美对虾树，导致更大规模的文本密码.从拓扑图形密码中可以选出毛毛虫树以及由这些毛毛虫树产生的随机对虾树来产生文本密码，但无法从这些文本密码重构原来的拓扑图形密码，因为中间的毛毛虫树或对虾树是无法确定的.

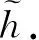
问题1毛毛虫树或对虾树有多少个不同的奇优美标号？

图3中，毛毛虫树H的主路P=u1u2u3u4u5上的每个顶点都可以在H的某一个奇优美标号中被标为零，相应地采用对偶标号，就可以把H的每一个叶子也标为零.在图3中，毛毛虫树H的奇优美标号(a)和(b)是一对对偶奇优美标号；同样地，图3中毛毛虫树H的奇优美标号(e)和(f)也是一对对偶奇优美标号.这种特性可以帮助人们设计随机型拓扑图形密码.

下面进一步解释毛毛虫树H中顶点标号为零的重要性.图4(a)给出了一颗毛毛虫树H的一个奇优美标号，顶点u3标号为零，H中顶点标号的最大值为23；图4(b)给标号为零的顶点u3添加了三片叶子，若新形成的图记为H1，则H1也是一棵毛毛虫树，且可以看成是图4(a)毛毛虫树H的“生长”.对于H1的标号，只需在保留H中标号的前提下，给新添加的三个一度顶点依次标号为25,27,29，就可得到H1的一个奇优美标号，且顶点标号的最大值和最小值分别为29和0；图4(c)中首先对图H1中各个顶点的标号进行修改，用29与原有标号值的差来作为H1中各个顶点的新标号值，那么原来标号为29的一度顶点的新标号值变为0，接着从这个顶点出发，又可以“生长”出五片叶子，将这五个一度顶点的标号依次标为31,33,35,37,39，就可得到新“生长”的树H2的一个奇优美标号，且顶点标号的最大值和最小值分别为39和0；图4(d)首先对图H2中各个顶点的标号进行修改，用39与原有标号值的差来作为H2中各个顶点的新标号值，那么原来标号为39的一度顶点的新标号值变为0，接着从这个顶点出发，又可以“生长”出两片叶子，将这两个一度顶点的标号依次标为41,43，就可得到新“生长”的树H3的一个奇优美标号.重复以上步骤，不断将标号为零的顶点变换到叶子上，再在该叶子上继续“生长”叶子，就可将原来的毛毛虫树不断“壮大”，且通过上述方法很容易得到“长大”的树的一个奇优美标号.这种随机增长的具有奇优美标号的树产生随机的密码，可以给使用者带来方便，并在一定程度上防范密码破译.