高中生数学逆商问卷的初步编制*

南宁市第二中学(530029) 于成宽 刘存华 李昕

1 引言

近20 年来,国内外学者对于“逆商”的关注持续升温,研究范畴囊括多个领域,涉及研究对象的职业以及年龄阶层十分多样. 以学生为研究对象,在教育范畴内进行逆商的学科化研究更是成为国内外学者的研究热点. 其中,在数学教育界,对于数学逆商的研究已经初具雏形,众多研究表明数学逆商是影响学生学业成绩的主要因素之一. 例如: Darmawan等人[1]认为,数学逆商高者的数学成绩显著高于其于同学.张怡和武小鹏[2]报告, 高中生的数学逆商和数学成绩存在0.65 的显著正相关. 另外地,数学逆商还影响着学生的数学理解、自我效能感、成就动机、数学焦虑等等. 例如: Hidayat等人[3]研究表明,数学逆商对数学理解能力有51.4%的积极影响. Bambang 等人[4]分析得出,成就动机与数学逆商紧密相关. 王芳[5]调查得知,数学焦虑和数学逆商存在显著负相关. 由此可知,提升学生的数学逆商有利于缓解数学焦虑、提升自我效能感、数学理解, 进而促进对数学的学习. 众所周知,高中的数学课程相较初中而言,在课程难度、课程内容、学习方法等方面对学生提出了更为高标准的要求,从而更易导致部分学生产生厌学、畏学、焦虑等负面情绪. 据已有文献得知,当前学生的数学逆商普遍不高. 例如杨顺才[6]在其硕士论文中提出,初中生的数学逆商处中等水平. 刘存华[7]以壮族学生为对象进行调查发现,壮族高中的数学逆商水平处于“较好”与“较低”的临界水平.

根据对179 篇“逆商”主题相关的文献综述[8]得知,当前对于逆商的研究有以下几点可待完善: 研究对象亟待“均衡化”(以高中生为样本的研究仅占7.3%左右);测量工具有待“自主化”(测量工具多为APR 量表); 研究方向有待“学科化”(多为逆商整体化研究,缺乏学科方向的逆商研究).

综合上述关于逆商的研究现状综述以及数学逆商的重要性,有必要编制一份具有良好信效度的,又具有本土化特色的高中生数学逆商问卷.

2 方法

2.1 高中生数学逆商的概念界定及理论构建

本量表对于数学逆商的概念缘取自张定强教授和曹春艳博士[9]的概念,数学逆商指学生在数学学习过程中所遇苦难和挫折的应对智力和能力. 其包含四个维度,该四个维度是将保罗·史托兹[10]提出的逆商概念进行数学学科化,具体释义如下:

表1 数学逆商的四因素模型

2.2 问卷题目的初步确定

根据数学逆商定义及其四个子维度的释义,咨询6 名数学教育方向专家(2 名教授、2 名博士、2 名一线教师)以及经过20 名数学教育方向研究生进行逐题修改后确定40 个题项,由此编制了各维度10 个题项的初测问卷.

2.3 施测对象

初测对象: 在北海市某高中的高二年级按照实验班、尖子班、普通版进行梯度化抽取210 名学生,以班级为单位采用纸质问卷进行测试,测试前进行调查说明和指导,测试时间大约15 分钟. 学生基本信息如下: 发放问卷210 份,回收有效问卷199 份,回收率94.7%,其中男生72 人(文科12 人,理60 人),女生127 人(文科43 人,理科84 人).

正式施测: 依据2019 年高考成绩,梯度化选取了南宁市第二中学、南宁市第八中学、南宁市外国语学校共计678 名高中生作为调查对象. 学生的基本信息如下: 男生307 人,女生371 人;汉族290 人,少数民族388 人.

2.4 施测与统计

研究以班级为单位进行施测, 并采用SPSS21.0 对回收的有效问卷进行项目分析、效度检验、信度检验. 首先采用临界比值法、量表题项与总分的相关、因素负荷量做项目分析,然后采用主成分分析法进行层面因素分析,以检验问卷的建构效度,最后通过Cronbachα系数以及折半信度来分析问卷的可靠性与有效性,以再测信度来了解问卷的一致性. 再将筛选之后的问卷用于南宁市三所学校进行调查,从而得到正式问卷的信度,再次验证问卷的有效性.

3 结果

3.1 项目分析(临界比值法)

首先进行逆商量表题项的加总,然后将总分进行“升序”排列得到低分组的临界值,同理进行“降序”排列得到高分组临界值,最后进行27%的高低分组,并进行极端组比较(独立样本T 检验). 保留t 统计量大于3.000,并达到显著水平(p＜0.05)的题项,t统计量小于3.000、结果不显著的题项鉴别度较差,一般考虑剔除.

初测问卷的独立样本t检验统计结果中的t值和p值如下表(表3)所示:

表3 独立样本t 检验统计结果中的t 值和p 值

由上述t检验的结果中, 第2 题、第6 题、第14 题检验的t 值未达显著(pA2= 0.173＞0.05,pA6= 0.070＞0.05,pA14= 0.207＞0.05) , 其余的三十七道题的极端组平均数差异检验的t检验均达到显著水平. 值得注意的是, 第10 题的t值虽达显著, 但其统计量略低(t= 2.304,p= 0.023) , 鉴别度较差, 可以考虑删除. 因此,将A2、A6、A10、A14 剔除以提高量表题项的鉴别度.

3.2 题项与总分之间的相关

通过计算各题项得分与各层面得分的相关系数,若相关系数未达显著(**表示在0.01 的水平上相关显著,*表示在0.05 的显著水平上相关显著),或两者为低相关(相关系数小于0.4),则意味着该题项与总分的同质性不高,建议剔除.

由上述表格(表4)可知,四个子维度各题项与总分的相关系数都在0.442 以上,而且均在0.01(双尾)水平上显著,说明各项目与层面总分的积差相关系数较高.

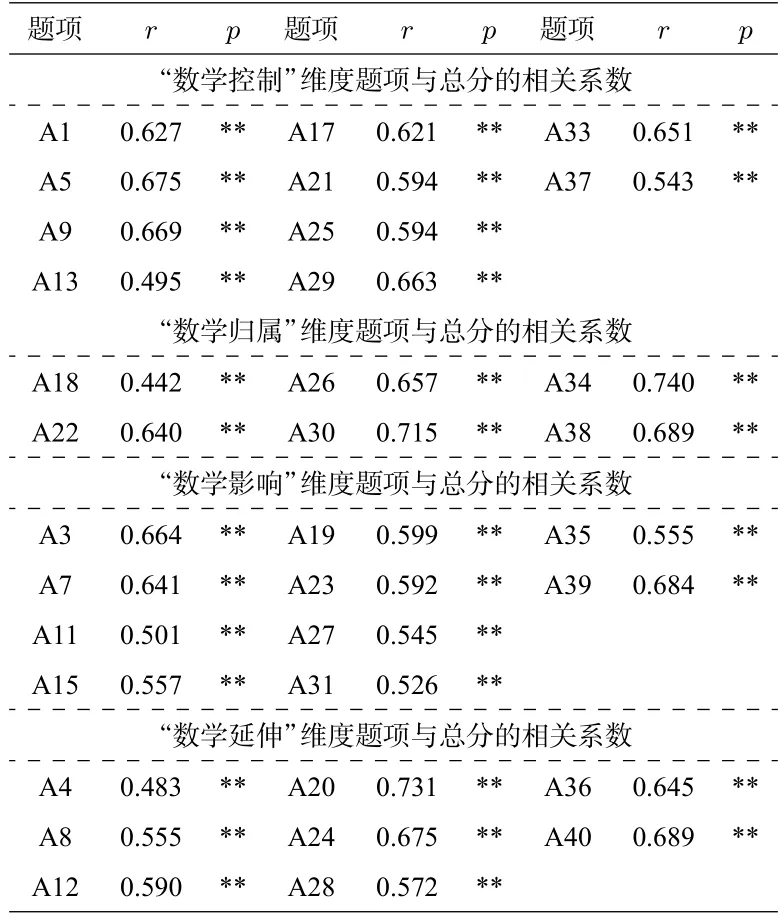
表4 各层面题项与总分的相关性

3.3 探索性因素分析

(1)KMO 和Bartlett 球形检验

在进行因素分析之前,先根据KMO 抽样适当性参数和Bartlett 球形检验的数据判断量表是否适合进行因素分析. 对高中生数学逆商量表做KMO 和Bartlett 球形检验,具体结果如下表5:

表5 初测逆商量表的KMO 和Bartlett 球形检验

在上述检验结果中,KMO 值等于0.836,表示达到良好程度,即“数学逆商”量表适合进行因素分析;Bartlett 球形检验的大约卡方为2796.446, 自由度为630, 显著性概率值为0.000,表示36 个题项变量有共同因素存在,数据文件适合进行因素分析.

(2)总问卷的探索性因素分析

采用“没有限定抽取因素法”, 先对问卷进行主成分分析,萃取出若干个共同因素,然后选择直交转轴的最大变异法求得各因素的负荷矩阵, 由此来确定问卷的因子数和每个因子下属的题项数. 确定因子和题项的原则: ①特征根大于1; ②题项载荷量至少在0.4 以上; ③变量共同度大于0.3;④每个因子至少含有3 个题项; ⑤提取出的因子符合陡阶检验.

如表6 所示,利用以上原则对数据进行探索性分析,删除19 个题项(18),剩余17 题. 其中,数学控制(C 维度)有三个题项,数学归属(O 维度)有五个题项,数学影响(R 维度)有六个题项,数学延伸(E 维度)有三个题项.

表6 数学逆商量表各题项的载荷、特征值和贡献率

通过对总问卷的探索性因素分析,一共提取出四个子维度,累计贡献率达54.418%,各个题项的因素负荷量除第35题为0.498 外,其余题项的负荷值均大于0.5. 根据因素分析所得题项内容,将主成分依次命名为: 数学影响、数学归属、数学延伸、数学控制,此四维度与预设一致.

(3)分层面进行探索性因素分析

由各层面进行因素分析结果可得, 四个维度都只萃取出一个主成分, 除A22(共同度为0.280)外的题项共同度均在0.339～0.699 范围内. 各题项的因素负荷量介于0.529 至0.836 间,因素负荷量在0.500 以上,表示萃取出的题项能够有效解释指标变量.

综上所述,从整体和分层面两个角度进行探索性因素分析可将“数学逆商”量表题项精简为17 题,并且各题项的共同度、负荷量均合理,累计解释变异量也处于43.924%～65.464之间,由此可知删减之后的初测问卷具有良好的建构效度.

3.4 信度检验

从表7 可知,高中生数学逆商总问卷的内部一致性信度系数值为0.792,属“可以接受”程度. 数学控制维度的克隆巴赫α系数属于“尚佳”(α= 0.686),另外三个层面的信度介于0.7～0.8,属“信度高”范围. 表明问卷具有一定的可靠性.

表7 高中生数学逆商问卷和各维度的信度检验

3.5 正式施测

本研究在正式施测时,数学逆商总量表及各维度的信度由下表8 可知: 高中生数学逆商量表的克隆巴赫α系数为0.802,数学控制、数学归属、数学影响、数学延伸的克隆巴赫α系数分别为0.612、0.706、0.800、0.764,根据众多学者的观点,总量表在0.7～0.8 之间属于可接受,分层面在0.6～0.8 之间属于尚佳层度, 且无论是编制问卷的预测还是正式施测,数学逆商的总量表及其各维度的信度均为良好且稳定,因此可用于测量高一学生的数学逆商.

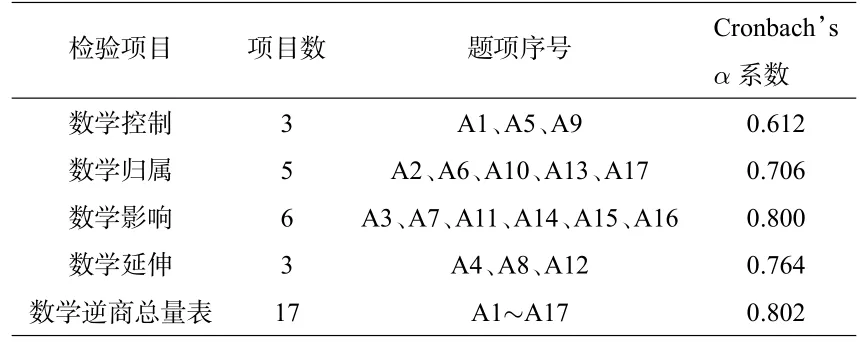
表8 数学逆商量表及其各维度的Cronbach’s α 系数

4 结论

(1)高中生数学逆商问卷的结构包括数学控制、数学归属、数学影响和数学延伸四个维度.

(2)自编的“高中生数学逆商问卷”具有良好的信度、效度,说明问卷适合作为测量高中生数学逆商水平的工具.